Экзамен по Шарову (Оптика 30-66). 30. Природа света

• Название: 30. Природа света
• Дата: 23.05.2023
• Размер: 2.91 Mb.
• Имя файла: Экзамен по Шарову (Оптика 30-66).docx
• Тип: Документы; #1154835
• страница: 8 из 15

§ 170. Насыщенность цветов. Кроме обозначения цвета — красный, желтый, синий и т. д.,— мы нередко различаем цвет по насыщенности, т. е. по чистоте оттен­ка, отсутствию белесоватости. Примером глубоких, или на­сыщенных, цветов являются спектральные цвета. В них представлена узкая область длин волн без примеси других цветов. Цвета же тканей и красок, покрывающих предметы, обычно бывают менее насыщенными и в большей или мень­шей степени белесоватыми. Причина лежит в том, что коэффициент отражения большинства красящих веществ не равняется нулю ни для одной длины волны. Та­ким образом, при осве­щении окрашенной тка­ни белым светом мы на­блюдаем в рассеянном свете по преимуществу одну область цвета (на­пример, красную), но к ней примешивается за­метное количество и дру­гих длин волн, дающих в совокупности белый свет. Но если такой рас­сеянный тканью свет с преобладанием одного цвета (например, крас­ного) направить не пря­мо в глаз, а заставить вторично отразиться от той же ткани, то доля преобладающего цвета значительно усилится по сравнению с остальными и белесоватость уменьшится.. Многократное повторение такого процесса (рис. 317) может привести к получению достаточно насыщенного цвета.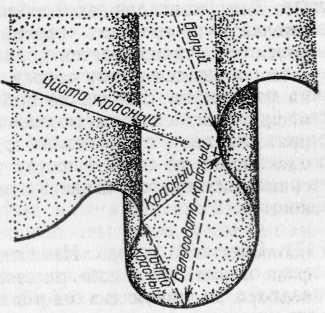



Рис. 317. Получение насыщенного цве­та при отражении от красной драпи­ровки

Если интенсивность падающего света какой-либо длины волны обоз­начить через I, а коэффициент отражения для той же длины волны — через , то получим после однократного отражения интенсивность I, после двукратного I², после трехкратного I³ и т. д. Отсюда видно, что если  для какого-то узкого спектрального участка равняется, напри­мер, 0,7, а для остальных равняется 0,1, то после однократного отраже­ния примесь белого цвета составляет 1/7, т. е. около 15%, после дву­кратного отражения 1/49, т. е. около 2%, и после трехкратного 1/343, т. е. меньше 0,3%. Такой свет можно считать вполне насыщенным.

Описанным явлением объясняется насыщенность цветов бархатных тканей, ниспадающих складками драпировок или реющих знамен. Во всех этих случаях имеются много­численные углубления (бархат) или складки окрашенной материи. Падая на них, белый свет претерпевает многократ­ное отражение, прежде чем достигнет глаза наблюдателя. При этом, конечно, ткань представляется более темной, чем, например, гладкая натянутая полоса цветного сатина; но насыщенность цвета увеличивается чрезвычайно сильно, и ткань выигрывает в красоте.

В § 167 мы упоминали, что поверхностный слой любой краски всегда рассеивает белый свет. Это обстоятельство портит насыщенность цветов картины. Поэтому картины, писанные масляными красками, обычно покрывают слоем лака. Заливая все неровности краски, лак создает гладкую зеркальную поверхность картины. Белый свет от этой по­верхности не рассеивается во все стороны, а отража­ется по определенному направлению. Конечно, если смот­реть на картину с неудачно выбранной позиции, то такой свет будет очень мешать {«отсвечивание»). Но если рассмат­ривать картину с других мест, то благодаря лаковому покрытию белый свет от поверхности в этих направлениях не распространяется, и цвета картины выигрывают в насы­щенности.

§ 171. Цвет неба и зорь. Изменение спектрального состава света, отраженного или рассеянного поверхностью тел, связано с наличием избирательного поглощения и отражения, выражающегося в зависимости коэффициентов  и  от длины волны.

В природе играет большую роль еще одно явление, ведущее к изменению спектрального состава солнечного света. Свет, доходящий до наблюдателя от участков безоб­лачного небесного свода, далеких от Солнца, характеризу­ется довольно насыщенным голубым или даже синим оттен­ком. Несомненно, что свет неба есть солнечный свет, рас­сеиваемый в толще воздушной атмосферы и по­этому доходящий до наблюдателя со всех сторон, даже по направлениям, далеким от направления на Солнце. Рис. 318 поясняет происхождение рассеянного света неба. Теоретическое исследование и опыты показали, что такое рассеяние происходит благодаря молекулярному строению воздуха; даже вполне свободный от пыли воздух рассеивает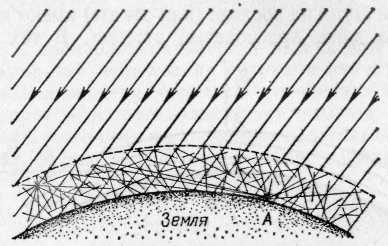



Рис. 318. Происхождение цвета неба (свет Солнца, рассеянный атмо­сферой). До поверхности Земли (например, точки А) доходит как пря­мой свет Солнца, так и свет, рассеянный в толще атмосферы. Цвет этого рассеянного света и называется цветом неба

солнечный свет. Спектр рассеянного воздухом света замет­но отличается от спектра прямого солнечного света: в сол­нечном свете максимум энергии приходится на желто-зеленую часть спектра, а в свете неба максимум передвинут к голубой части. Причина лежит в том, что короткие све­товые волны рассеиваются значительно сильнее длинных. По расчетам английского физика Джона Стретта лорда Рэлея (1842—1919), подтвержденным измерениями, интен­сивность рассеянного света обратно пропорциональна чет­вертой степени длины волны, если рассеивающие частицы малы по сравнению с длиной волны света, следовательно, фиолетовые лучи рассеиваются почти в 9 раз сильнее крас­ных. Поэтому желтоватый свет Солнца при рассеянии пре­вращается в голубой цвет неба. Так обстоит дело при рассея­нии в чистом воздухе (в горах, над океаном). Наличие в воз­духе сравнительно крупных частичек пыли (в городах) добавляет к рассеянному голубому свету свет, отраженный частичками пыли, т. е. почти неизмененный свет Солнца. Благодаря этой примеси цвет неба становится в этих усло­виях более белесоватым.

Преимущественное рассеяние коротких волн приводит к тому, что доходящий до Земли прямой свет Солнца оказы­вается более желтым, чем при наблюдении с большой высоты. На пути через толщу воздуха свет Солнца частично рассеивается в стороны, причем сильнее рассеиваются ко­роткие волны, так что достигший Земли свет становится от­носительно богаче излучением длинноволновой части спект­ра. Это явление особенно резко сказывается при восходе и закате Солнца (или Луны), когда прямой свет проходит зна­чительно большую толщу воздуха (рис. 319). Благодаря это­му Солнце и Луна на восходе (или закате) имеют медножелтый, иногда даже красноватый оттенок. В тех случаях,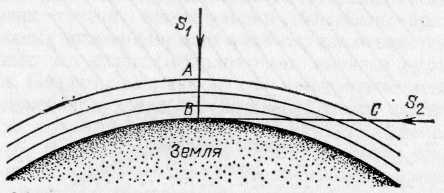



Рис. 319. Объяснение красного цвета Луны и Солнца на восходе и за­кате: S₁ — светило в зените — короткий путь в атмосфере (АВ); S₂ — светило на горизонте — длинный путь в атмосфере (СВ)

когда в воздухе имеются очень мелкие (значительно мень­шие длины волны) частички пыли или капельки влаги (туман), рассеяние, вызываемое ими, также идет по закону,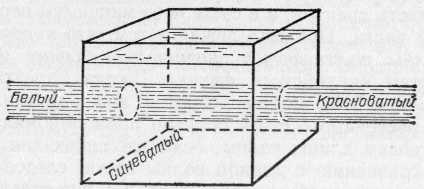



Рис. 320. Рассеяние света мутной жидкостью: падающий свет — белый, рассеянный свет — синеватый, проходящий свет — красноватый

близкому к закону Рэлея, т. е. по преимуществу рассеива­ются короткие волны. В этих случаях восходящее и захо­дящее Солнце может быть совершенно красным. В красный же цвет окрашиваются и плавающие в атмосфере облака. Таково происхождение прекрасных розовых и красных оттенков утренней и вечерней зорь.

Можно наблюдать описанное изменение цвета при рас­сеянии, если пропустить пучок света от фонаря через сосуд (рис. 320), наполненный мутной жидкостью, т. е. жид­костью, содержащей мелкие взвешенные частицы (напри­мер, водой с несколькими каплями молока). Свет, идущий в стороны (рассеянный), заметно синее, чем прямой свет фонаря. Если толща мутной жидкости довольно значитель­на, то свет, прошедший сквозь сосуд, теряет при рассеянии столь значительную часть коротковолновых лучей (синих и фиолетовых), что оказывается оранжевым и даже красным. В 1883 г. произошло сильнейшее извержение вулкана на острове Кракатау, наполовину разрушившее остров и вы­бросившее в атмосферу огромное количество мельчайшей пыли. На протяжении нескольких лет пыль эта, развеянная воздушными течениями на огромные расстояния, засоряла атмосферу, обусловливая интенсивные красные зори.

40. Линзы. Преломление изображения в линзах.

Преломление в линзе. Фокусы линзы. В гл. IX был сформулирован закон преломления света, устанавливаю­щий, как меняется направление светового луча при пере­ходе света из одной среды в другую. Был рассмотрен про­стейший случай преломления света на плоской гра­нице раздела двух сред.

В практических применениях очень большое значение имеет преломление света на сферической границе раздела. Основная деталь оптических приборов — линза — представляет собой обычно стеклянное тело, ограниченное с двух сторон сферическими поверхностями; в частном слу­чае одна из поверхностей линзы может быть плоскостью, которую можно рассматривать как сферическую поверх­ность бесконечно большого радиуса.

Линзы могут быть изготовлены не только из стекла, но, вообще говоря, из любого прозрачного вещества. В некото­рых приборах, например, применяются линзы из кварца, каменной соли и др. Заметим, что и поверхности линз могут быть также более сложной формы, например цилиндриче­ские, параболические и т. д. Однако такие линзы приме­няются сравнительно редко. В дальнейшем мы ограничимся рассмотрением линз со сферическими поверхностями.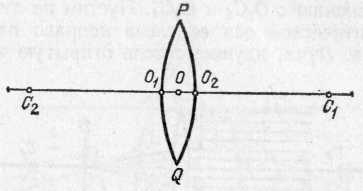



Рис. 193. Тонкая линза: О — оптический центр, С₁ и С₂ — центры огра­ничивающих линзу сферических поверхностей

Итак, рассмотрим линзу, ограниченную двумя сфериче­скими преломляющими поверхностями PO₁Qи PO₂Q(рис. 193). Центр первой преломляющей поверхности PO₁Qлежит в точке С₁, центр второй поверхности PO₂Q— в точ­ке С₂. На рис. 193 для ясности изображена линза, имеющая заметную толщину O₁O₂.В действительности мы будем обычно предполагать, что рассматриваемые линзы очень тонки, т. е. расстояние О₁О₂очень мало по сравнению с O₁C₁или О₂С₂.В таком случае точки О₁ и O₂ можно счи­тать практически сливающимися в одной точке О. Эта точка О называется оптическим центром линзы.

Всякая прямая, проходящая через оптический центр, называется оптической осью линзы. Та из осей, которая проходит через центры обеих преломляющих поверхностей линзы, называется главной оптической осью, остальные — побочными осями.

Луч, идущий по какой-либо из оптических осей, проходя через линзу, практически не меняет своего направления. Действительно, для лучей, идущих вдоль оптической оси, участки обеих поверхностей линзы можно считать параллельными, а толщину линзы мы считаем весьма малой. При прохождении же через плоскопараллельную пластинку, как мы знаем, световой луч претерпевает параллельное смеще­ние, но смещением луча в очень тонкой пластинке можно пренебречь (см. упражнение 26 после гл. IX).

Если на линзу падает световой луч не вдоль одной из ее оптических осей, а по какому-либо другому направлению, то он, испытав преломление сначала на первой ограничи­вающей линзу поверхности, потом на, второй, отклонится от первоначального направления.

Прикроем линзу черной бумагой 1 с вырезом, оставляю­щим открытым небольшой участок около главной оптиче­ской оси (рис. 194). Размеры выреза мы предполагаем малы­ми по сравнению с O₁С₁и O₂С₂.Пустим на линзу 2 вдоль главной оптической оси ее слева направо параллельный пучок света. Лучи, идущие сквозь открытую часть линзы,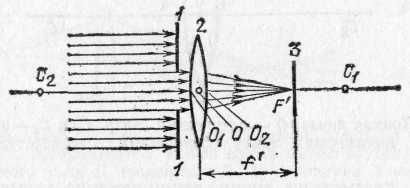



Рис. 194. Главный фокус линзы

преломятся и пройдут через некоторую точку F', лежащую на главной оптической оси, справа от линзы на расстоянии f' от оптического центра О. Если в точке F' расположить белый экран 3, то место пересечения лучей изобразится в виде яркого пятнышка. Эта точка F' на главной оптиче­ской оси, где пересекаются после преломления в линзе лучи, параллельные главной оптической оси, называется главным фокусом, а расстояние f^f'=OF' — фокусным расстоянием линзы.

Нетрудно показать, пользуясь законами преломления, что все лучи, параллельные главной оптической оси и про­ходящие через небольшую центральную часть линзы, после преломления действительно пересекутся в одной точ­ке, названной выше главным фокусом.

Рассмотрим луч РМ, падающий на линзу параллельно ее главной оптической оси. Пусть этот луч встречает первую преломляющую поверхность линзы в точке М на высоте hнад осью, причем hгораздо меньше, чем С₂О и С₁O(рис. 195). Преломленный луч пойдет по направлению ММ' и, преломившись снова на второй ограничивающей линзу поверхности, выйдет из линзы по направлению M'F', составляющему с осью угол . Точку пересечения этого луча с осью обозначим через F', а расстояние от этой точки до оптического центра линзы — через f'.

Проведем через точки М и М' плоскости, касатель­ные к преломляющим поверхностям линзы. Эти касатель­ные плоскости (перпендикулярные к плоскости чертежа) пересекутся под некоторым углом , причем угол  весьма мал, так как рассматриваемая нами линза — тонкая. Вместо преломления луча PMM'F' в линзе мы, очевидно, можем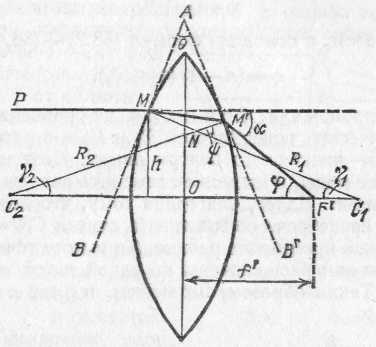



Рис. 195. Преломление в линзе луча РМ, параллельного главной оп­тической оси. (Толщина линзы и высота h изображены преувеличен­ными по сравнению с расстояниями R₁, R₂ и f''; в соответствии с этим и углы ₁₂ и  на рисунке чрезмерно велики.)

рассматривать преломление того же луча в тонкой призме ВАВ', образованной проведенными нами в точках М и М' касательными плоскостями.

Мы видели в § 86, что при преломлении в тонкой призме с преломляющим углом  луч отклоняется от первоначаль­ного направления на угол, равный

(88.1)

где nесть показатель преломления вещества, из которого сделана призма. Очевидно, угол  равен углу  (рис. 195), т. е.

(88.2)

Пусть C₁и С₂ — центры сферических преломляющих по­верхностей линзы, a R₁и R₂ — соответственно радиусы этих поверхностей. Радиус C₁Mперпендикулярен к касательной плоскости АВ, а радиус С₂М' — к касательной плоскости АВ'. По известной теореме геометрии угол между этими перпендикулярами, который мы обозначим равен углу  между плоскостями:

(88.3)

С другой стороны, угол , как внешний угол в треугольнике C₁NC₂,равен сумме углов ₁ и ₂, образуемых радиусами R₁и R₂с осью:

(88.4)

Таким образом, с помощью формул (88.2) — (88.4) находим

(88.5)

Мы предположили, что h мала по сравнению с радиу­сами сферических поверхностей R₁и R₂ и с расстоянием f' точки F' от оптического центра линзы. Поэтому углы ₁, ₂и  также малы, и мы можем заменить синусы этих углов самими углами. Далее, благодаря тому, что линза тонкая, мы можем пренебречь ее толщиной, считая C₁O=R₁; C₂O=R₂,а также пренебречь разницей в высоте точек М и М', считая, что они расположены на одной и той же высоте hнад осью. Таким образом, мы можем приближенно считать, что

(88.6)

Подставляя эти равенства в формулу (88.5), найдем

(88.7)

или, сокращая на h,

(88.8)

отсюда

(88.9)

Весьма существенно, что hне входит в оконча­тельный результат. Это означает, что любой луч, параллельный главной оптической оси линзы, встре­чающий линзу на любом, но достаточно малом по сравнению с R₁ и R₂расстоянии hот оси, пройдет после пре­ломления в линзе через одну и ту же точку F', лежащую на расстоянии f' от оптического центра линзы.

Таким образом, доказано, что линза имеет главный фокус, и формула (88.9) показывает, как фокусное расстояние зависит от показателя преломления вещества, из которого сделана линза, и от радиусов кри­визны ее преломляющих поверхностей.

Мы предполагали, что параллельный пучок лучей падает на линзу слева направо. Существо дела не изменится, ко­нечно, если на линзу направить такой же пучок лучей, идущих в обратном направлении, т. е. справа налево. Этот пучок лучей, параллельных главной оси, соберется снова в одной точке F— втором фокусе линзы (рис. 196) на расстоянии f от ее оптиче­ского центра. На основании формулы (88.9) заключаем, что f=f', т. е. оба фокуса лежат симметрично по обе стороны линзы *).

Фокус Fназывается обычно передним фокусом, фокус F' — задним фоку­сом; соответственно этому расстояние f называется передним фокусным рас­стоянием, расстояние f' — задним фокусным расстоя­нием.

Если в фокусе линзы поместить точечный источник света, то каждый из лучей, выйдя из этой точки и преломив­шись в линзе, пойдет далее параллельно главной оптиче­ской оси линзы, в согласии с законом обратимости световых лучей (см. § 82). Таким образом, из линзы выйдет в этом слу­чае пучок лучей, параллельных главной оси.

При практическом применении полученных нами соот­ношений необходимо всегда помнить о сделанных при вы­воде их упрощающих предположениях. Мы считали, что параллельные лучи падают на линзу на очень малом расстоянии от оси. Это условие не выполняется вполне строго. Поэтому после преломления в линзе точки пересе­чения лучей не будут строго совпадать между собой, а зай­мут некоторый конечный объем. Если мы поставим в этом месте экран, то получим на нем не геометрическую точку,

*) Этот вывод связан с тем обстоятельством, что мы с самого начала полагаем, что по обе стороны линзы находится одна и та же среда (воз­дух). Если бы это было не так, то нарушилась бы и симметрия в располо­жении фокусов Fи F',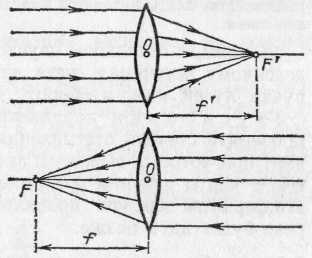



Рис. 196. Фокусы линзы

а всегда более или менее расплывчатое светлое пят­нышко.

Другое обстоятельство, которое нужно помнить, состоит в том, что мы не можем осуществить строго точечный источ­ник света. Поэтому, поместив в фокусе линзы источник хотя бы очень малых, но всегда конечных разме­ров, мы не получим с помощью линзы строго парал­лельный пучок лучей.

В § 70 было указано, что строго параллельный пучок лучей не имеет физического смысла. Сделанное замечание показывает, что рассмотрен­ные свойства линзы находятся в согласии с этим общим физическим по­ложением.

В каждом отдельном случае применения линзы к опре­деленному источнику света для получения параллельного пучка лучей или, наоборот, при применении линзы для фокусировки параллельного пучка надо специально проверять степень отступления от тех упрощающих усло­вий, при которых выведены формулы. Но существен­ные черты явления преломления световых лучей в линзе эти формулы передают правильно, а об отступлениях от них речь будет идти позже.

41. Формула линзы. Действительное и мнимое изображение.

Изображение в линзе точек, лежащих на главной оп­тической оси. Формула линзы. Пусть точечный источник света находится в точке S на главной оптической оси линзы, на расстоянии а от ее оптического центра О (рис. 197). Рас­смотрим, как будет преломляться в линзе узкий пучок лучей, примыкающий к прямой SO, являющейся осью этого пучка *).

Пусть один из лучей (SM) светового пучка падает на первую преломляющую поверхность линзы в точке М, находящейся на высоте hнад осью. То обстоятельство, что мы ограничиваемся узким пучком лучей, означает, что hмало по сравнению с расстоянием а от источника до линзы. С другой стороны, так же как и в § 88, будем считать, что hмало по сравнению с f', а следовательно, и по сравнению с радиусами R₁и R₂ ограничивающих линзу поверхностей. Угол, образуемый лучом SMс осью, обозначим . Так как hмало, то и угол мал. Преломленный луч пойдет по на­правлению ММ' и, преломившись снова на второй ограни­чивающей линзу поверхности, выйдет из линзы по направ­лению M'S', составляющему с осью угол '. Обозначим через а' расстояние от оптического центра линзы до точки S', в которой преломленный луч пересекает главную ось.

*) Такие пучки обычно называют параксиальными (приосевыми).

Как и в предыдущем параграфе, проведем через точ­ки М и М' плоскости, касательные к преломляющим по­верхностям линзы. Эти плоскости образуют тонкую призму ВАВ' с преломляющим углом . Вместо того чтобы рас­сматривать преломление луча SMM'S' в линзе, будем рас­сматривать преломление того же луча в тонкой призме ВАВ'.

Выбранный нами луч после преломления отклонится от первоначального направления на угол а, который по фор­муле тонкой призмы равен

(89.1)

где n— показатель преломления вещества, из которого сделана линза.

Рассмотрим также луч РМ, идущий параллельно глав­ной оси и падающий на линзу в точке М. Преломление та­кого луча уже рассмотрено в § 88 (условие малости hздесь соблюдено). Мы знаем, что после преломления в линзе этот луч выйдет из точки М" под углом  к оси и пройдет через главный фокус F' на расстоянии f' от оптического центра.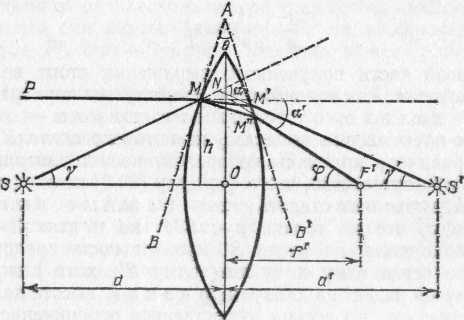



Рис. 197. Преломление в линзе луча SM, выходящего из точки S на оси. Угол ВАВ' и толщина линзы сильно преувеличены

Точки М' и М" очень близки друг к другу, так что призмы, образованные касательными в точке М и точках М' или М", практически не различаются и имеют один и тот же прелом­ляющий угол . Угол ', на который отклонится этот луч от первоначального направления после преломления в тон­кой призме, равен опять (n—1), т. е. равен углу . С дру­гой стороны, этот угол ' равен, очевидно, углу  (рис. 197).

Таким образом, получаем

(89.2)

Но угол а как внешний угол в треугольнике SNS' равен сумме +'. Итак, имеем

(89.3)

Лучи SM, M'S' и M"F' идут под небольшими углами к оси, т. е. углы , 'и  малы. Заменяя, как и в предыдущем параграфе, синусы малых углов самими углами и прене­брегая толщиной линзы и разницей в высоте точек М, М' и М" над осью, можно приближенно написать:

(89.4)

Подставляя эти приближенные равенства в формулу (89.3), находим

(89.5)

или, сокращая на общий множитель h,

(89.6)

В правой части полученного выражения стоит величина 1/f', которая, как мы видели в предыдущем параграфе, за­висит только от свойств линзы — от пока­зателя преломления вещества, из которого сделана линза, и от радиусов кривизны ее преломляющих поверхностей.

То обстоятельство, что в формулу (89.6) не входит вели­чина h, позволяет сделать очень важные выводы, а именно, что не только луч SM, но и всякий другой луч, выходящий из точки S, пройдет после преломления в линзе через одну и ту же точку S', хотя каждый из этих лучей падает на линзу на разной высоте над осью. Единственное, но весьма существенное ограничение, кото­рое мы накладываем на рассматриваемые лучи, состоит в том, что все они составляют с осью линзы малые углы.

Таким образом, все лучи узкого пучка, выходящие из точки S, соберутся после преломления в линзе снова в одной точке S', являющейся изображением точки S. Мы доказали, следовательно, что образующееся в тонкой линзе изобра­жение точечного источника, лежащего на главной оси линзы, полученное с помощью достаточно узкого пучка лучей, явля­ется точкой.

Изображения, при получении которых выполнено ус­ловие передачи каждой точки объекта одной точкой изображения, носят название стигматических. Изображения, у которых это условие не соблюдено, носят название астигматических *).

Отметим, что в силу закона обратимости световых лучей (§ 82) положения источника света Sи его изображения S' обратимы, т. е., поместив источник в S', мы полу­чим его изображение в точке S. Точки S и S' называются сопряженными.

В геометрической оптике особое значение имеет задача получения стигматических изображений. Степень стигматичности изображений определяет качество служащих для их получения оптических систем. Нарушение оптической системой стигматичности падающих на нее световых пучков ведет к расплывчатости изображения. В дальнейшем при изучении простейших оптических систем мы будем уделять большое внимание вопросу о стигматичности даваемых ими изображений.

Полученная нами формула (89.6) связывает между собой расстояния от оптического центра трех точек, находящихся на главной оси линзы: источника S, его изображения S' и фокуса F'. Это — основная формула тонкой линзы.