Экзамен по Шарову (Оптика 30-66). 30. Природа света

• Название: 30. Природа света
• Дата: 23.05.2023
• Размер: 2.91 Mb.
• Имя файла: Экзамен по Шарову (Оптика 30-66).docx
• Тип: Документы; #1154835
• страница: 4 из 15

§ 128. Пучки лучей и форма волновой поверхности. Для очень большого круга вопросов, где успешно применялись построения геометрической оптики, мы характеризовали распространение света при помощи лучей. Образование параллельного пучка лучей означало, что световая энергия распространяется лишь по направлению этого пучка, не рас­сеиваясь в стороны, так что освещенность поверхности, на которую падает свет, остается неизменной на любом расстоянии от источника. Расходящийся пучок лучей озна­чал распределение света по возрастающей поверхности, так что освещенность уменьшалась обратно пропорци­онально квадрату расстояния от точки, из которой расхо­дятся лучи (вершина пучка). Наоборот, сходящийся пучок ;лучей означал возрастание освещенности по мере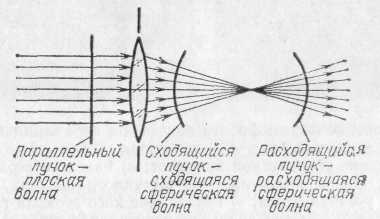



Рис. 270. Изменение формы фронта волны при прохождении через

линзу

приближения к точке схождения лучей. Роль оптических си­стем сводилась к преобразованию формы волновых фронтов. С точки зрения волновых представлений распростране­ние света есть распространение волн, а роль лучей играют линии, перпендикулярные к поверхности фронта волны. Характер распространения света задается формой фронта волны (волновой поверхностью). Так, параллельный пучок лучей соответствует плоской волне, фронт которой имеет форму плоскости, перемещающейся парал­лельно самой себе. Сходящиеся в точке или расхо­дящиеся из точки пучки соответствуют сферическим волновым поверхностям, центр которых лежит в точке схож­дения или расхождения лучей. Изменение кривизны фронта волны означает изменение угла схождения лучей.

Таким образом, прохождение волны через систему линз или зеркал сводится к изменению формы ее фронта (рис. 270).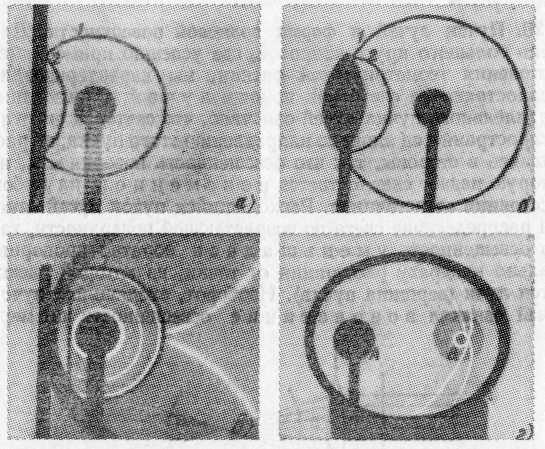



Рис. 271. Изменение формы фронта волны при отражении (фотографии звуковой волны в воздухе: 1 — падающая волна, 2 — отраженная волна). Отражение сферической волны от: а) плоского зеркала — кри­визна фронта волны неизменна; б) выпуклого зеркала — кривизна фронта волны увеличивается; в) параболического зеркала (источник — в фокусе зеркала) — фронт волны становится плоским; г) эллиптиче­ского зеркала (источник — в фокусе А зеркала) — волна сходится

в фокусе В

Влияние отражения от разных поверхностей на форму фронта волны хорошо иллюстрируется на ряде снимков, приведенных на рис. 271 и изображающих отражение зву­кового импульса в воздухе. Аналогичные картины могут быть без труда получены и при наблюдении преломленных волн.

§ 129. Принцип Гюйгенса. Рисунки, представленные в предыдущем параграфе, дают лишь общее качествен­ное понятие о волновом характере распространения све­та и о действии отражения и преломления на световую волну.

Но еще Гюйгенс сумел использовать представление о распространении волн в среде для количественного расчета законов преломления и отражения. С этой целью им был сформулирован общий принцип, которому подчиня­ется распространение волн. Этот принцип Гюйгенса пред­ставляют собой правило, позволяющее, исходя из положе­ния волнового фронта в какой-нибудь момент времени, найти положение волнового фронта для ближайшего более позднего момента времени.

Согласно принципу Гюйгенса каждую точку среды, ко­торой достигла волна, можно рассматривать как источник вторичных сферических волн, распространяющихся со ско­ростью, свойственной среде. Огибающая поверхность, т. е. поверхность, касающаяся всех сферических вторичных волн в том положении, которого они достигнут к моменту вре­мени t, и представляет собой волновой фронт в этот момент.

Поверхность, на которой расположены точки среды, выбранные в качестве источников вторичных волн, является для построения Гюйгенса вспомогательной по­верхностью. Она не должна обязательно совпадать с поло­жением какого-либо волнового фронта, но может быть по­верхностью, до которой первичные волны доходят в раз­ные моменты времени.

Для отыскания же фронта волны к моменту tнадо пост­роить положение вторичных волн к этому моменту и про­вести огибающую поверхность. Таким образом, из точек, достигнутых первичной волной в более ранний момент, вто­ричные волны успеют разойтись на большие расстояния, а из точек, позже принятых за центр вторичных волн,— на меньшие.

Принцип Гюйгенса дает возможность найти интересую­щую нас огибающую, выбирая вспомогательную поверхность различными способами, но окончательный результат, ко­нечно, будет один и тот же. На рис. 272 рассматривается рас­пространение сферической расходящейся волны, фронт кото­рой в некоторый момент времени t₀ занимает положение Р₀. В разные точки вспомогательной поверхности Р свет от источника приходит в разные моменты времени. Таким об­разом, при применении принципа Гюйгенса можно выби­рать центры вторичных волн наиболее удобным для решения данной задачи способом. Благодаря этому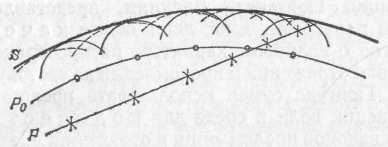


Рис. 272. К пояснению принципа Гюйгенса: Р₀ — вспомогательная поверхность, совпадающая в момент t₀=0 с положением фронта сфери­ческой расходящейся волны; соответствующие вторичные волны (цент­ры — светлые кружки) изображены сплошными дугами; Р — произ­вольная вспомогательная поверхность; соответствующие вторичные волны (центры — крестики) изображены штриховыми дугами; S — волновая поверхность в момент t, построенная как огибающая вторич­ных волн

принцип Гюйгенса с большой пользой применяется при раз­боре различных вопросов о распространении волн. Один из примеров такого применения мы найдем в следующем параграфе.

§ 130. Законы отражения и преломления света на основе принципа Гюйгенса. Пусть на границу раздела двух сред аb(рис. 273) падает параллельный пучок лучей, образуя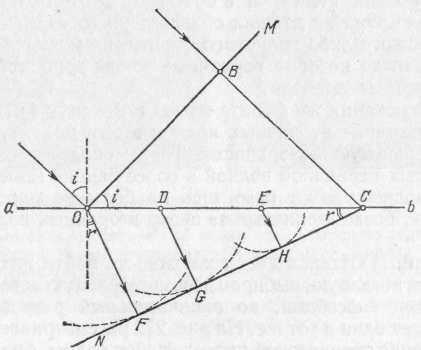


Рис. 273. К нахождению закона преломления волн. ОВ — поверхность падающей волны, ab — поверхность раздела двух сред, NC — поверх­ность преломленной волны

угол i с перпендикуляром к поверхности раздела. Согласно закону преломления пучок преломленных лучей будет рас­пространяться по направлению, задаваемому углом r. Закон преломления, выведенный из опыта, гласит:



где n— показатель преломления второй среды относитель­но первой,— есть величина, не зависящая от угла паде­ния света iи характеризующая свойства обеих сред.

Согласно волновым представлениям опи­санная задача сводится к следующему. На поверхность раз­дела падает плоская волна, поверхность которой со­ставляет угол iс поверхностью раздела. Скорость распрост­ранения волны в первой среде есть v₁,во второй — v₂.

Для нахождения закона преломления и показателя преломления воспользуемся принципом Гюйгенса. Задача решается без труда, если мы выберем в качестве центров вторичных волн точки, лежащие на границе раздела. Пусть в момент времени t=0падающая плоская волна до­стигает в точке О границы раздела, т. е. поверхность падаю­щей волны имеет положение ОМ, Найдем положение огиба­ющей к моменту t=, когда точка В поверхности падающей волны успеет достигнуть границы раздела в точке С. Так как скорость волны в первой среде есть v₁, то расстояние ВС рав­но v₁. Вторичная волна из точки О успеет за это время рас­пространиться во второй среде на расстояние OF=v₂. Точ­ка Dбудет достигнута первичной волной несколько позже, и вторичная волна от нее успеет к моменту т проникнуть во вторую среду на меньшую глубину, равную DG; от точки Е глубина проникновения будет еще меньше — ЕН;от точки С к моменту т распространение волны еще не начнется, ибо к этому моменту точка С только будет достигнута пер­вичной волной. Построив огибающую, которая оказывается плоскостью, касающейся всех вторичных сферических волн, найдем линию CN— положение фронта преломленной волны; этот фронт распространяется во второй среде со скоростью v₂ по направлению OF (CN), задаваемому уг­лом r.

Из ОВС и COFнайдем соотношение между углами i и r, т. е. закон преломления. Действительно, BC=v₁=ОСsini, OF=v₂=OC sinr, откуда



Если обозначить отношение v₁/v₂через n, то получим закон преломления в обычной его форме sini/sinr=n. Величина nне зависит от углов i и r и носит название показателя преломления.

Мы не только нашли путем рассуждений Гюйгенса пра­вильный закон преломления, но и объяснили физиче­ский смысл показателя преломления n: показатель преломления равен отношению скорости свето­вой волны в первой среде к скорости ее во второй.

Если первая среда воздух (или вакуум, что для многих вопросов практически одно и то же), а вторая — вода, то из опыта известно, что n=1,33. Таким образом, наши рассуж­дения приводят к выводу, что скорость света в воздухе (вакууме) в 1,33 раза больше, чем в воде. Мы увидим (§ 153), что прямые измерения скорости света в воде и в воздухе подтверждают этот вывод.

Аналогичным способом можно рассмотреть явления от­ражения волны. Мы найдем закон отражения: угол отраже­ния равен углу падения.

§ 131. Принцип Гюйгенса в толковании Френеля. Изложен­ное в предыдущем параграфе наглядно показывает плодот­ворность принципа Гюйгенса для решения многих важных задач оптики. В формулировке Гюйгенса принцип этот имел характер геометрического правила, согласно которому результат действия вторичных волн мо­жет быть найден построением поверхности, огибающей эти волны. Французский физик Огюстен Френель (1788—1827), заимствовав из принципа Гюйгенса представление о вто­ричных волнах, применил к ним законы интерференции. Согласно Френелю правило построения огибающей должно быть заменено расчетом взаимной интерференции вторич­ных волн; такой расчет приводит к тем же результатам, что и первоначальное правило Гюйгенса.

Способ Френеля не только вкладывает более глубокое физическое содержание в принцип Гюйгенса, но и делает возможным решение ряда новых задач, которые не могли быть исследованы по первоначальному методу Гюйгенса.

Пусть, например, волна распространяется в однород­ной среде по определенному направлению. Любая точ­ка, до которой дойдет волна, становится источником вто­ричных волн, которые разбегаются во все стороны. Может показаться, что благодаря этому первоначальное направле­ние распространения изменится и световая волна рассеется в стороны. Однако если учесть, согласно Френелю, взаим­ную интерференцию этих вторичных волн, то окажется, что в боковых направлениях вторичные волны взаимно уничтожают друг друга и лишь в первоначальном направлении они взаимно усиливаются. Поэтому свет распространяется лишь в первоначальном направлении. Мы приходим, следователь­но, к объяснению прямолинейного распространения света в однородной среде.

Если, однако, среда неоднородна, например содержит посторонние включения или состоит из различных сред (на­пример, в воздухе расположены зеркала, пластинки, лин­зы и т. д.), то результат будет иной. Свет при прохождении через такую сложную среду не распространяется прямоли­нейно, а рассеивается в стороны или испытывает отражения, преломления и т. д. Мы видели, например, в § 130, как с помощью принципа Гюйгенса можно получить количест­венные законы преломления и отражения.

Таким образом, все основные законы геометрической оп­тики — закон прямолинейного распространения, закон пре­ломления, закон отражения — оказалось возможным ис­толковать с волновой точки зрения с помощью принципа Гюйгенса — Френеля.

Еще более важным является то обстоятельство, что с по­мощью этого принципа можно рассмотреть, как протекают оптические явления при условиях, когда законы геометри­ческой оптики перестают быть справедливыми.

§ 132. Простейшие дифракционные явления. Простей­ший случай нарушения законов геометрической оп­тики был описан в § 80, где было показано, что в случае прохождения света через очень малое отверстие не соблю­дается правило прямолинейного распространения: свет на краях отверстия заметно отклоняется в стороны, огибая края. Такого рода огибание можно при внимательном наблюдении обнаружить при отбрасывании на экран те­ни от любого препятствия, даже если оно не очень мало. Но так как угол отклонения света от направления прямо­линейного распространения обычно невелик, то наблюде­ние облегчится, если экран расположить далеко от пре­пятствия.

Так, свет, идущий от небольшого яркого источника че­рез круглое отверстие диаметра d(рис. 274, а), должен по правилам геометрической оптики дать на экране ММ резко ограниченный светлый кружок на темном фоне (рис. 274, б). Такая картина и наблюдается практически при обычных условиях опыта. Но если расстояние от отверстия до экра­на в несколько тысяч раз превосходит размеры отверстия, то удается наблюдать важные детали явления: образуется более сложная картина, которая состоит из совокупности светлых и темных концентрических колец, постепенно пере­ходящих друг в друга (рис. 274, в).При другом соотноше­нии между диаметром отверстия и расстоянием до экрана в центре картины может быть темное пятно. Этот случай осо­бенно наглядно характеризует волновые свойства света и совершенно необъясним с позиции геометрической оптики (подробнее см. § 133).



Рис. 274. Дифракция от круглого отверстия: а) схема опыта; б) вид

тени, когда диаметр отверстия d сравним с расстоянием D от отверстия

до экрана; в) вид тени, когда диаметр отверстия d в тысячи раз меньше

расстояния D от отверстия до экрана

Таким образом, для наблюдения описанного случая ди­фракции надо применить или очень малое отверстие (сотые доли миллиметра, если мы хотим сделать опыт на лаборатор­ном столе) или прибегнуть к расположению экрана на боль­шом расстоянии от отверстия (сотни метров, если мы хотим работать с отверстиями в несколько миллиметров).

Точно так же при освещении маленьким источником до­статочно больших непрозрачных предметов, расположенных сравнительно недалеко от экрана, получаем вполне резкие тени. Но если расстояние от предмета до экрана значи­тельно превосходит размеры предмета, то тень приобретает сложный характер.

На рис. 275, а изображена тень от прямолинейного пред­мета (проволочки или карандаша), отброшенная на отда­ленный экран. Внутри тени наблюдаются области, куда заходит свет, а края тени окаймлены рядом светлых и тем­ных полос. На рис. 275, б изображена тень от шурупа, полу­ченная в таких же условиях. Сложный характер картины показывает, что свет значительно уклоняется от прямых линий, загибаясь около краев и давая ряд светлых и темных областей, лишь отдаленно напоминающих резкую тень, подобную предмету. На рис. 275, в изображена тень руки, держащей тарелку. Опыты были осуществлены в 1912 г. В. К. Аркадьевым и А. Г. Калашниковым в Московском уни­верситете и проводились с уменьшенной моделью руки с та­релкой. Расстояния от модели до экрана, проставленные на рисунке, пересчитаны для опыта с тарелкой натуральной величины. Чем дальше расположен экран, тем меньше сход­ство между очертаниями тени и предмета *).


Рис. 275. Фотографии дифракционных картин (тень отбрасывается на

экран): а) дифракция от проволоки (I) и карандаша (II); б) дифракция

от шурупа; в) дифракция от руки, держащей тарелку, при различном

расстоянии от руки до экрана

Описанные выше явления нару­шения закона прямолинейного рас­пространения света получили на­звание дифракции света.

§ 133. Объяснение дифракции по методу Френеля. Отступления от законов прямолинейного распрос­транения света, примеры которых приведены в предыдущем парагра­фе, получают простое объяснение с точки зрения волновой теории и являются естественным следствием этой теории. Действительно, наб­людаемое в каждом случае распре­деление света есть результат ин­терференции вторичных волн.

Рассмотрим, например, прохож­дение света через круглое отверстие DDв экране (рис. 276). Для того чтобы рассчитать интенсивность света в точке О, применим следую­щий вспомогательный прием. Про­ведем из точки О конические поверх­ности OKL, OMN, OPQи т. д. до пе­ресечения с поверхностью сферичес­кой волны DCD. Длины образую­щих выберем так, что OL=OC+/2, ON=OL+/2и OQ=ON+/2и



Рис. 276. К объяснению явления дифракции на круглом отверстии. Вни­зу — схематическое изоб­ражение наблюдаемой картины: а) при нечетном числе зон; б) при четном числе зон

т. д. Другими словами, расстояние от точек С, L, N, Q, ... до точки О возрастает на длину полуволны (/2)

*) Приведенные фотографии осуществлены проф. В, К. Аркадье­вым и заимствованы из его статьи.

света, падающего на отверстие. Поверхность волны DCDразобьется на кольцевые зоны. Площади этих зон практиче­ски одинаковы, ибо ОС значительно больше /2.Но действие их в точке О различно. Действительно, разность хода до точки О между какой-либо точкой первой зоны и соот­ветствующей точкой второй зоны равняется /2.Поэтому световые волны от первой и второй зон, дойдя до О, будут взаимно ослабляться, так что в точке О действие первой зоны практически уничтожается действием второй зоны. Совер­шенно подобные же рассуждения покажут, что в точке О действие третьей зоны противоположно действию второй, действие четвертой — противоположно действию третьей и т. д, и вообще действия соседних зон практически уничто­жают друг друга. Если отверстие DDтаково, что в нем уме­щаются всего две зоны, то в точке О почти не будет света, ибо две соседние зоны взаимно ослабляют друг друга. Большая часть света будет распределена вокруг точки О, так что мы увидим темное пятно, окружен­ное светлым кольцом. При размере отверстия в три зоны в точке О должен быть свет, ибо третья зона ослабит действие второй, и точка будет освещена почти неослаблен­ным действием полной первой зоны» Светлая цен­тральная точка будет охвачена тем­ным кольцом, за которым вновь наблюдается просвет­ление. Вообще при четном числе зон в центре будет темное пятно, окруженное чередующимися светлыми и темными кольцами; при нечетном числе зон — в центре светлее пят­но, а ближайшее кольцо темное и т. д. Размеры этих колец тем меньше, чем больше диаметр отверстия, так что при боль­шом диаметре темные и светлые кольца около центра чере­дуются настолько часто, что мы перестаем различать их и практически не замечаем явлений дифракции.

Аналогичным образом могут быть поняты и другие, бо­лее сложные дифракционные картины. Так как расчет зон Френеля зависит от длины волны света, то, следовательно, и вид дифракционной картины будет зависеть от длины волны. Опыт вполне подтверждает это за­ключение. В частности, в белом свете кольца будут цвет­ными.