Экзамен по Шарову (Оптика 30-66). 30. Природа света

• Название: 30. Природа света
• Дата: 23.05.2023
• Размер: 2.91 Mb.
• Имя файла: Экзамен по Шарову (Оптика 30-66).docx
• Тип: Документы; #1154835
• страница: 12 из 15

§ 106. Хроматическая аберрация. Поставим на пути све­товых лучей, выходящих из линзы 1, один раз красное стек­ло (пропускающее только красные лучи), другой раз синее стекло (пропускающее синие лучи). С помощью передвиж­ного экрана 2 (рис. 235) мы обнаружим, что изображения,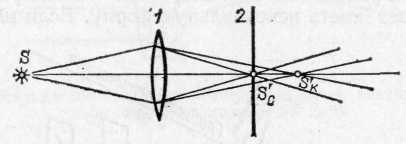



Рис. 235. Хроматическая аберрация: изображение точки S в синих

лучах S'_c не совпадает с изображением в красных лучах S'_к. Рисунок

имеет цветной дубликат (см. форзац)

образуемые лучами разного цвета, находятся в разных точках: S'_к(красное) дальше от линзы, чем S'_с(синее). Если же оставить экран в том месте, где образуется резкое изображение, например синими лучами, то в красном свете мы получим на экране расплывчатое пятнышко. Вследствие этого при использовании белого света (содержащего лучи всех цветов) изображение, даваемое линзой, оказывается обычно окрашенным (окаймленным цветными кружками и т. п.). Описанное явление носит название хроматической аберрации.

Эта погрешность возникает вследствие того, что показа­тель преломления зависит от длины волны света (дисперсия; см. § 83). Из-за этого и фокусное расстояние линзы, ко­торое согласно формуле (88.9) зависит от показателя пре­ломления, будет различным для лучей различного цвета. В результате изображения точки S для лучей различ­ного цвета будут находиться на разных расстояниях от линзы.

Расстояние между точками S'_cи S'_кзависит от сорта стекла, из которого сделана линза: оно больше для той лин-

*) Частица а перед словом означает отрицание: астигма­тизм — неточечность изображения; ана — двойное отрица­ние (вместо аа) анастигматизм — неастигматизм, т. е, точечность изображения,

зы, которая сделана из стекла с большей дисперсией *) (если сравниваемые линзы имеют одинаковое фокусное расстояние для лучей какого-либо цвета). Это обстоятельство использу­ется для устранения хроматической аберрации линз следу­ющим образом. К двояковыпуклой линзе из стекла с малой дисперсией приклеива­ется соответствующим образом рассчитанная рассеивающая линза из стекла с большой дис­персией (рис. 236). До­бавочная линза удлиня­ет фокусные расстояния первой линзы (см. § 104), причем фокусное рассто­яние синих лучей, сильнее преломляемых, увеличивается в большей степени, чем фокусное расстояние красных лу­чей, слабее преломляемых. Расчет в простейшем случае ведется таким образом, чтобы фокус красных лучей F'_к и фокус синих лучей F'_cпопали в одну и ту же точку F'. Соединившись в одном месте, изображения разных цветов дадут практически белую точку, т. е. хроматическая абер­рация будет устранена.

Линзы с устраненной описанным способом хроматической аберрацией называются ахроматическими линзами. Применяются также систе­мы, где соединены фокусы для трех сортов лучей,— апохроматы. Такие апохроматические системы используются, например, в микроскопии.

§ 107. Ограничение пучков в оптических системах. Изучая оптические системы, мы до сих пор оставляли в стороне

одно важное обстоятельство — ограниченность размеров линз (или зеркал), образующих системы. Оправданием этому

служило то, что для построения изображения не требуется знать реальный ход всех лучей в системе; например, для построения изображения точки достаточно построить два

луча, которые, вообще говоря, могут в действительности и не проходить через прибор (см. рис. 216).

Вследствие ограниченного размера любой оптической системы большая часть лучей, выходящих из светящегося объекта по всем направлениям, проходит мимо системы и не

может участвовать в образовании изображения. Всякая преграда, ограничивающая проходящие через оптическую

систему лучи, называется диафрагмой. В случае простой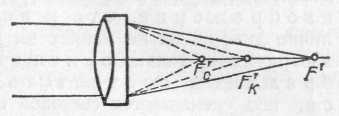



Рис. 236. Исправление хроматической аберрации. Рисунок имеет цветной дуб­ликат (см. форзац).

*) То есть из стекла с показателем преломления, сильнее меняющим­ся с изменением длины волны падающего света,

линзы диафрагмой служит обычно ее оправа. Однако можно часть линзы закрыть, например, поставив перед ней лист картона, в котором вырезано отверстие; в этом случае диа­фрагмой служит данное отверстие в картоне. При этом надо иметь в виду, что любая часть линзы (если она достаточно хорошо исправлена *)) образует то же изображение, что и вся линза; поэтому на­личие диафрагмы не меняет ни размера, ни вида изображения; только освещенность этого изо­бражения соответственно уменьшается, ибо уменьшается световой поток, пропускаемый при наличии диафрагмы. Можно, например, закрыть половину линзы куском картона — изображение останется тем же, но освещенность его в этом случае уменьшится в два раза, так как в образовании изображения будет участвовать только половина пучка.

Таким образом, для хорошо исправленной системы роль диафрагмы прежде всего сводится к изменению светового потока, участвующего в образовании изображения. Диафраг­ма определяет также поле зрения прибора, т. е. максималь­ную часть объекта, изображение которого может дать прибор. Значение диафрагмы для получения изображений протяженных предметов (глубины фокусировки) мы не будем рассматривать; о влиянии диафрагмы на разрешаю­щую способность оптических приборов см. в гл. XIV.

§ 108. Светосила линзы. Найдем, как зависит освещенность изображения, даваемого линзой, от величин, характе­ризующих линзу,— от ее диаметра и фокусного расстояния. Освещенность изображения Е определяется отношением светового потока Ф к поверхности изображения ', т. е. Е=Ф/'. При заданном расстоянии а от источника до линзы световой поток, поступающий от источ­ника через линзу к изображению, пропорционален площади линзы, т. е. пропорционален d², где d— диаметр линзы или диафрагмы, прикрывающей линзу. Площадь изображения прямо пропорциональна квадрату расстояния а' изображения от линзы; если же источник находится да­леко от линзы, то изображение находится вблизи фокаль­ной плоскости и площадь изображения пропорциональна квадрату фокусного расстояния f². Таким образом, в данном случае освещенность изображения пропорциональна (d/f)².

*) То есть устранены погрешности, указанные выше,

Действительно, пусть около точки S(рис. 237) помещается пло­щадка и около точки S' — ее изображение '. Пользуясь формулой увеличения линзы, находим: '/—а'²/а². Далее по формуле линзы

1/a+1/a'=1/f или a'/a=f/(a—f). Если расстояние а от источника до

линзы гораздо больше fто в знаменателе правой части можно пренеб­речь f по сравнению с а, и тогда a'f, а ' пропорциональна f².

Итак, освещенность изображения, даваемого линзой, пропорциональна квадрату ее диаметра и обратно пропор­циональна квадрату ее фокусного расстояния. Величина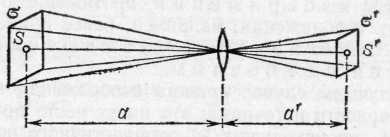



Рис. 237. К выводу формулы для освещенности изображения, даваемо­го линзой

(d/f)²называется светосилой линзы. Эта величина характе­ризует свойства линзы в отношении освещенности давае­мых ею изображений. Нередко для характеристики линзы вместо светосилы (d/f)² пользуются величиной d/f, именуе­мой относительным отверстием.

Мы видим, что освещенность изображения уменьшается при ограничении светового пучка, вступающего в линзу. Это относится ко всякому оптическому прибору. Но в то же время качество изображения при ограничении пучка улучшается.

Таким образом, хорошее качество изображе­ния трудно сочетать с большой светосилой при­бора.

Практически приходится идти на некоторый компромисс и допускать некоторую потерю в светосиле для получения надлежащего качества изображения и, наоборот, мириться с ухудшением качества изображения для получения доста­точной его освещенности.

В современных оптических приборах удается в извест­ных пределах сочетать большую светосилу с хорошим ка­чеством изображения за счет использования многолинзовых оптических систем. В подобных системах аберрации, вноси­мые одними линзами, компенсируются аберрациями дру­гих линз. Простейшие примеры исправления оптических систем мы приводили, говоря о сферической и хроматической аберрациях и об астигматизме. Следует отметить, что расчет сложных оптических систем представляет большие трудности, требует значительного искусства и затраты дли­тельного времени.

§ 109. Яркость изображения. В предыдущем параграфе мы видели, что освещенность изображения протяженного предмета повышается с увеличением диаметра линзы и с уменьшением ее фокусного расстояния. Могло бы показаться, что этим путем можно повысить также яркость изображения протяженного предмета и получить изображения, например, более яркие, чем сам источник. Однако подобное заключение ока­зывается ошибочным.

В наилучшем случае яркость изображения может до­стигнуть яркости источника; это имеет место при отсутст­вии потерь, происходящих за счет частичного поглощения света в линзах и частичного отражения его поверхностями линз. При наличии потерь света в системе яркость изобра­жения протяженного объекта всегда меньше яркости самого объекта. Получить яркость изображения протяженного объекта, большую чем яркость источника, нельзя никакими оптическими приборами.

Невозможность увеличить яркость изображения с по­мощью оптической системы становится понятной, если вспомнить основное свойство всякой системы, отмеченное в § 102. Оптическая система, не имеющая потерь, не меняет светового потока, но она, уменьшая площадь изображения, во столько же раз увеличивает те­лесный угол, в который направляется световой поток. При уменьшении площади изображения световой поток, испускаемый единицей поверхности, увеличивается, но зато этот поток направляется в больший телесный угол. Таким образом, световой поток, испускаемый единицей по­верхности в единичный телесный угол, т. е. яркость (см. §73), остается неизменным.

Для простого случая образования изображения с помощью линзы мы можем подтвердить этот общий вывод путем несложного расчета. Поместим перед линзой на расстоянии а от нее небольшую светя­щуюся поверхность с площадью , перпендикулярную к главной оси. Пусть ее изображение находится на расстоянии а' от линзы и имеет площадь '. Тогда, очевидно (рис. 238), /' =а²/a'², или

(109.1)

Найдем световой поток, направляющийся от источника через лин­зу. Согласно формуле (73.2) Ф=L, где L— яркость светящейся пло­щадки,  — ее площадь, a —телесный угол потока, направляемого к линзе. Из рис. 238 видно, что =A/a², где А — площадь отверстия линзы. Итак,

(109.2)

Этот световой поток направляется на изображение '.

Световой поток, испускаемый изображением, направляется внутрь телесного угла ', который, как видно из рис. 238, равен '=А/а'².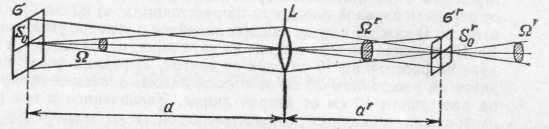



Рис. 238. Яркость изображения зависит от произведения телесного угла на площадь изображения и не может превысить яркости источника

Поток, идущий от изображения, равен Ф'=L''', где L' есть яркость изображения. Итак,

(109.3)

Если в линзе не происходит потерь света, то оба световых потока — Падающий на линзу (и направляемый ею к изображению) Ф и исходя­щий от изображения Ф' — должны быть равны друг другу:



Отсюда в силу (109.1)

(109.4)

т. е. яркость изображения, даваемого линзой, равна яркости самого объекта. Напомним, что все выводы справедливы лишь для протяжен­ных объектов. Вопрос о яркости изображения точечных объектов мы рассмотрим в следующей главе.

Полученный результат позволяет найти освещенность изображе­ния, даваемого линзой. Для освещенности изображения, согласно фор­муле (109.3), имеем

(109.5)

Если можно пренебречь потерями света в линзе, то L'=Lи, следовательно

(109.6)

Мы видим, что освещенность изображения, получаемого с помо­щью линзы, такая же, как если бы мы заменили линзу источником той же яркости Lи с площадью, равной площади линзы. Полученная фор­мула (109.6) применима и к более сложным системам.

Яркость изображения может быть повышена и превзойти яркость источника, если в пространстве между источником и изображением на­ходится активная среда, усиливающая проходящее через нее излучение. (Способы создания активных сред будут рассмотрены позже.) Системы с усилением яркости называются активными оптическими системами. Примером такой системы может служить лазерный проекционный микро­скоп, позволяющий получать на экране площади несколько квадратных метров изображения микроскопических объектов с освещенностью, достаточной для восприятия в незатемненном помещении. В активных оптических системах энергия передается изображению из активной среды.

51. Различные виды микроскопов, используемые в судебной экспертизе.

Разрешающая способность микроскопов. Степень прониковения в микромир, изучения микромира зависит от возможности рассмотреть величину микрообъектов, от разрешающей способности прибора, определяемой длиной волны используемого в микроскопии излучения (видимое, ультрафиолетовое, рентгеновское излучение). Фундаментальное ограничение заключается в невозможности получить при помощи электромагнитного излучения изображение объекта, меньшего по размерам, чем длина волны этого излучения. «Проникнуть глубже» в микромир возможно при применении более коротковолновых излучений, т.е. излучений с меньшими длинами волн, с более высокой разрешающей способностью микроскопов.

В зависимости от требуемой величины разрешения рассматриваемых микрочастиц материи, микроскопы разделяются на Оптические; Электронные; Рентгеновские; Лазерные рентгеновские микроскопы.

Оптический микроскоп. Оптическая система микроскопа состоит из основных элементов - объектива и окуляра. Они закреплены в подвижном тубусе, расположенном на металлическом основании, на котором имеется предметный столик. В современном микроскопе практически всегда есть осветительная система (в частности, конденсор с ирисовой диафрагмой), макро- и микро- винты для настройки резкости, система управления положением конденсора. В зависимости от назначения, в специализированных микроскопах могут быть использованы дополнительные устройства и системы.

Электронный микроскоп отличается возможностью получать сильно увеличенное изображение объектов, используя для их освещения электроны. В отличие от оптического микроскопа, в электронном микроскопе используют потоки электронов и магнитные или электростатические линзы. Некоторые электронные микроскопы позволяют увеличивать изображение в 2 млн. раз, в то время, как максимальное увеличение лучших оптических микроскопов достигает 2000 раз. Как электронные, так и оптические микроскопы имеют ограничения в разрешающей способности в зависимости от длины волн. В электронных микроскопах используются электростатические или электромагнитные линзы для формирования изображения путем управления пучком электронов и концентрации его на отдельных участках изображения подобно тому, как оптический микроскоп использует стеклянные линзы для фокусирования света на (или сквозь) изображении.

Рентгеновский микроскоп - устройство для исследования микроскопического строения вещества с помощью рентгеновского излучения. Разрешающая способность достигает 100нм, что в 2 раза выше, чем у оптических микроскопов (200нм). Теоретически рентгеновская микроскопия позволяет достичь на 2 порядка лучшего разрешения, чем оптическая (поскольку длина волны рентгеновского излучения меньше на 2 порядка). Однако современный оптический микроскоп - наноскоп имеет разрешение до 3-10нм. Различают рентгеновские микроскопы отражательные и проекционные.

Лазерный рентгеновский микроскоп - прибор или микроскоп c применением рентгеновских лазерных лучей отличающийся разрешающей способностью, обеспечивающей получение изображений на субатомном, атомном уровне на базе использования генерируемого вынужденного луча, например, (инфракрасного) мощностью 14,2 киловатта с длиной волны 1,61 ангстрема.(Например, в ходе химической реакци в режиме 3D и др.).

Применение микроскопов:

Биологические микроскопы применяются для лабораторных биологических и медицинских исследований прозрачных объектов. Доступны «режимы» светлого и темного поля, фазовый контраст, поляризованный свет.

Металлографические микроскопы применяются в научных и промышленных лабораториях для исследования непрозрачных объектов. Возможна работа в отраженном и проходящем свете. Доступны режимы светлого и темного поля, фазовый контраст, поляризованный свет.

Стереоскопические микроскопы применяются в лабораториях и на различных производствах для получения увеличенных изображений объектов во время проведения рабочих операций. Возможна работа в отраженном и проходящем свете.

Поляризационные микроскопы применяются в научных и исследовательских лабораториях для специализированных исследований в поляризованном свете. Возможна работа в отраженном и проходящем свете.