35 Моделирование тенденции временного ряда. 35 Моделирование тенденции временного ряда
 Скачать 1.88 Mb. Скачать 1.88 Mb.
|
Метод Гольдфельда-Квандта проверки гипотезы гомоскедастичностиСреди основных предположений регрессионного анализа важную роль играет предположение гомоскедастичности, которое заключается в равенстве дисперсий наблюдений: Возможны различные нарушения этого предположения в рамках парной регрессии. Одно из распространенных нарушений связано с тем, что дисперсия наблюдения может возрастать вместе с ростом значения фактора (объясняющей переменной): так, например, если Обнаружение этого нарушения может быть осуществлено с помощью критерия Гольдфельда-Квандта. Кратко применение критерия можно описать следующим образом:
4) вычислим статистику 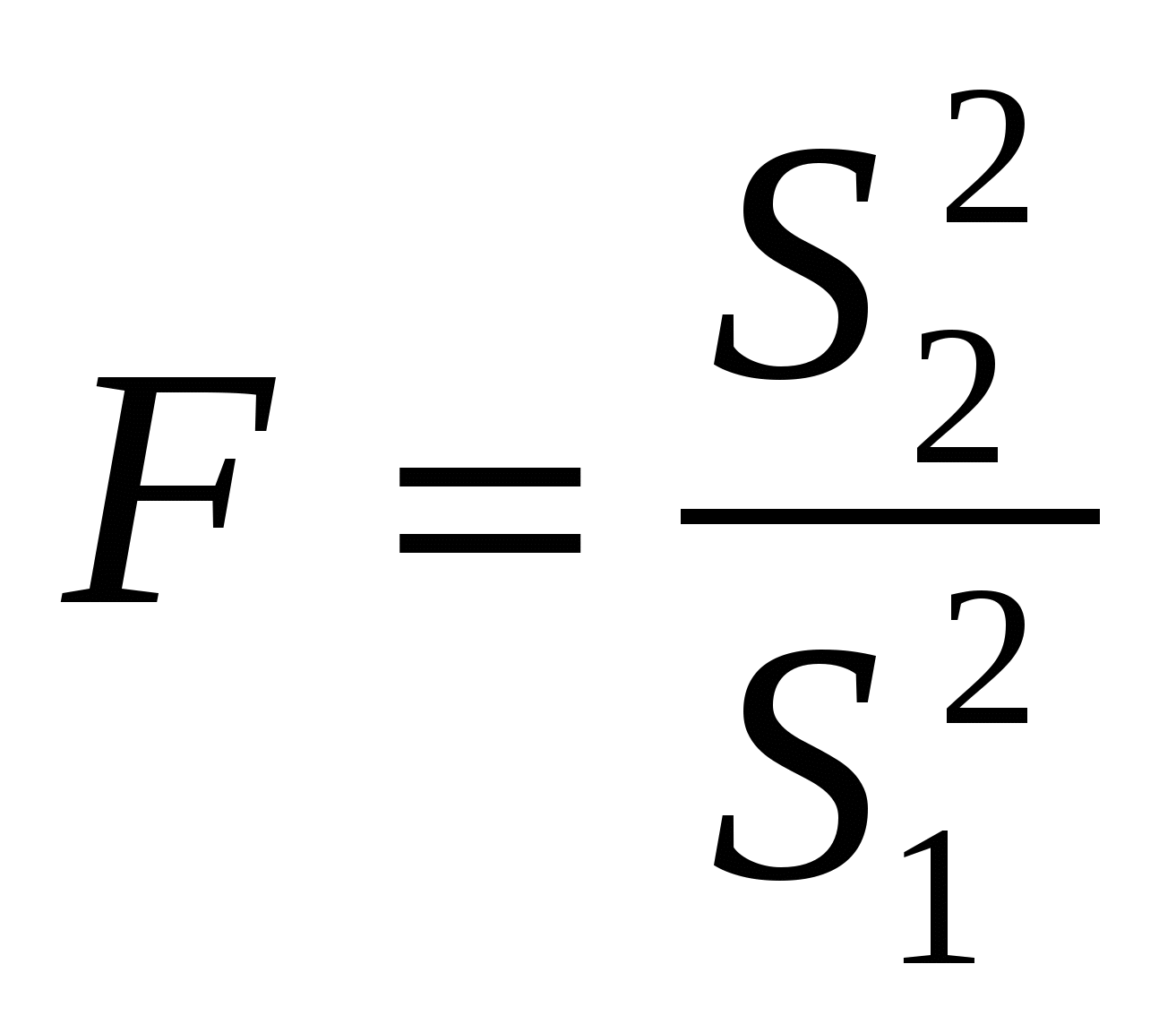 , если верна гипотеза гомоскедастичности , если верна гипотеза гомоскедастичности Найдем табличное значение По значению вычисленной статистики 1) Если 2) Если 27 Гомоскедастичность остатков регрессионной функции. Гетероскедастичность остатков регрессионной функции. Дисперсия - среднее арифметическое из квадратов отклонений наблюденных значений (x1, x2,...,xn) случайной величины от их среднего арифметического.Гомоскедастичностьостатков означает, что для каждого значения фактора xj остатки 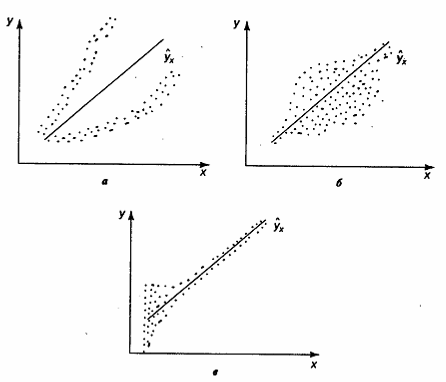 а— дисперсия остатков растет по мере увеличения х; б —дисперсия остатков достигает максимальной величины при средних значениях переменной хи уменьшается при минимальных и максимальных значениях х; в —максимальная дисперсия остатков при малых значениях х и дисперсия остатков однородна по мере увеличения значений х. Наличие гомоскедастичности или гетероскедастичности можно видеть и по графику зависимости остатков Бо 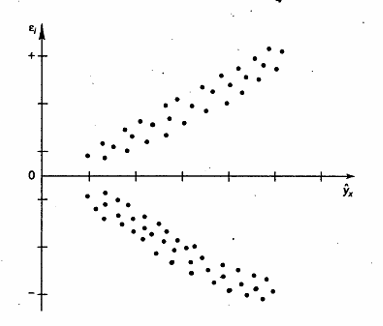 льшая дисперсия льшая дисперсияГетероскедастичность будет сказываться на уменьшении эффективности оценок При этом величина 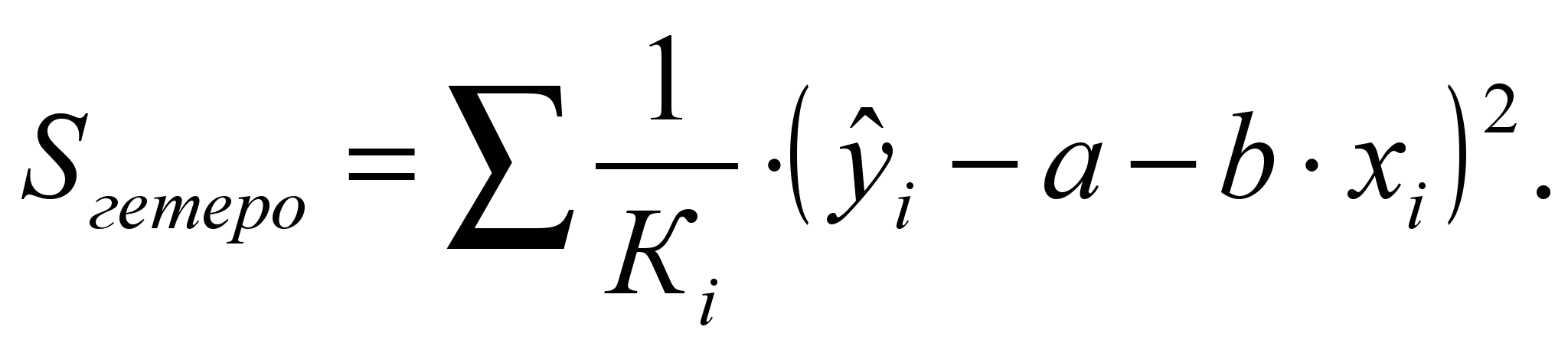 При минимизации этой суммы квадратов отдельные ее слагаемые взвешиваются: наблюдениям с наибольшей дисперсией придается пропорционально меньший вес. Задача состоит в том, чтобы определить величину При малом объеме выборки для оценки нарушения гомоскедастичности можно использовать метод Гольдфельда-Квандта, который включает: 1.Упорядочение наблюдений n по мере возрастания переменной х. 2. Исключения из рассмотрения центральных наблюдений C; при этом 3. Разделение совокупности 4. Определение остаточной суммы квадратов для обеих групп 26 Предпосылки метода наименьших квадратов. При оценке параметров уравнения регрессии применяется МНК. При этом делаются определенные предпосылки относительно составляющей Исследования остатков 1) случайный характер остатков. С этой целью строится график отклонения остатков от теоретических значений признака. Если на графике получена горизонтальная полоса, то остатки представляют собой случайные величины и применение МНК оправдано. В других случаях необходимо применить либо другую функцию, либо вводить дополнительную информацию и заново строить уравнение регрессии до тех пор, пока остатки не будут случайными величинами. 2) нулевая средняя величина остатков, т.е. 3.Гомоскедастичность— дисперсия каждого отклонения 4. Отсутствие автокорреляции остатков. Значения остатков 5. Остатки подчиняются нормальному распределению. В тех случаях, когда все пять предпосылок выполняются, оценки, полученные по МНК и методу максимального правдоподобия, совпадают между собой. Если распределение случайных остатков 25 фиктивные переменные во множественной регрессии при построении уравнения множественной регрессии может оказаться необходимым включение в модель фактора, имеющего 2 и более качественного уровня. Например, это атрибутивные признаки – пол, профессия, образование, климатические условия и т.д. чтобы ввести такие переменные в регрессионную модель им присваиваются цифровые метки, т.е. качественные переменные преобразуются в количественные. Такого вида структурированные переменные называются фиктивные. Пример, по группе Х м и ж пола изучается линейная зависимость потребления кофе от цены, у- потребление кофе, х – цена. Y=a+bx; y1=a1+b1x+E1-Mужчины, y2=a2+b2x+E2-женщины. Из этих 2 уравнений нужно получить 1 уравнение. Y=a1z1+a2z2+bx+E Z1= В отдельном случае, может оказаться необходимость введения 2 и более фиктивных переменных, тогда модель представляет собой сумму y=a1z1+a2z2+a2s3+a4s4+bx+E Фиктивные переменные для оценки сезонных различий потреблений. Фиктивные переменные могут вводиться не только в линейные, но и не в линейные модели, но приводимые к линейным с помощью некоторых преобразований. 21. основные элементы временных рядов Построить эконометрическую модель можно, используя 2 типа данных: 1. данные, характеризуют совокупность объектов в определенный момент или период времени. 2. данные, характеризующие один объект за несколько последовательных моментов или периодов времени. Модели, построенные по данным первого типа, называются пространственными моделями. модели, построенные по данным 2 типа, называются моделями временных рядов. Временной ряд- совокупность значений какого-либо показателя за несколько моментов или периодов времени. Каждый уровень временного ряда формируется под воздействием большого числа факторов, которые условно можно разделить на 3 группы: 1. факторы, формирующие тенденцию ряда. 2. фактора, формирующие циклические колебания ряда. 3. случайные факторы. При различных состояниях изучаемого явления этих факторов зависимость уровня ряда от времени может быть различие. Во-первых, большинство временных рядов экономических показателей имеет тенденцию, характеризующую совокупное долговременное воздействие множества факторов на исследуемый показатель. Во-вторых, изучаемый показатель может быть подвержен циклическим колебаниям. Эти колебания могут носить сезонный характер, т.к. экономическая деятельность ряда отраслей экономики зависит от времени года. Некоторое временные ряды не содержат тенденции и циклические компоненты. А их каждый следующий уровень образуется как сумма следующего уровня ряда и некоторого положительной или отрицательной компоненты. В большинстве случаев фактический уровень временного ряда может представлять собой сумму или произведение трендовой, циклической и случайной компонент. Модель, в которой временной ряд представлен как сумма перечисленных компонент называется аддитивной. Модель, в которой временной ряд представляет собой произведение 3 компонент называется мультипликативной. Основные компоненты временного ряда.  Тенденция циклическая случайная Основная задача эконометрического исследования временных рядов- выявление и предание количественного выражения каждой из перечисленных компонент с тем, чтобы использовать полученную информацию для прогнозирования будущих значений ряда. 22 частная корреляция частные индексы корреляции характеризуют тесноту связи исследуемого признака и одним из факторов при устранении влияния остальных факторов, включенных в модель. Эти показатели представляют собой отношение сокращения остаточной дисперсии за счет включения доп. Факторов. Если рассматриваемая регрессия с числом факторов Р, то возможны коэффициенты корреляции первого, второго и т.д. Р-1 порядков, т.е. пример: действие влияния Х1 можно оценить при разных условиях независимого действия др. факторов: ryx1x2 при постоянном действии фактора Х2, ryx1x2x3 при постоянном действии факторов Х2 и Х3. формула в общем виде имеет вид: 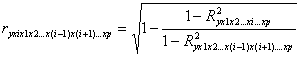 |

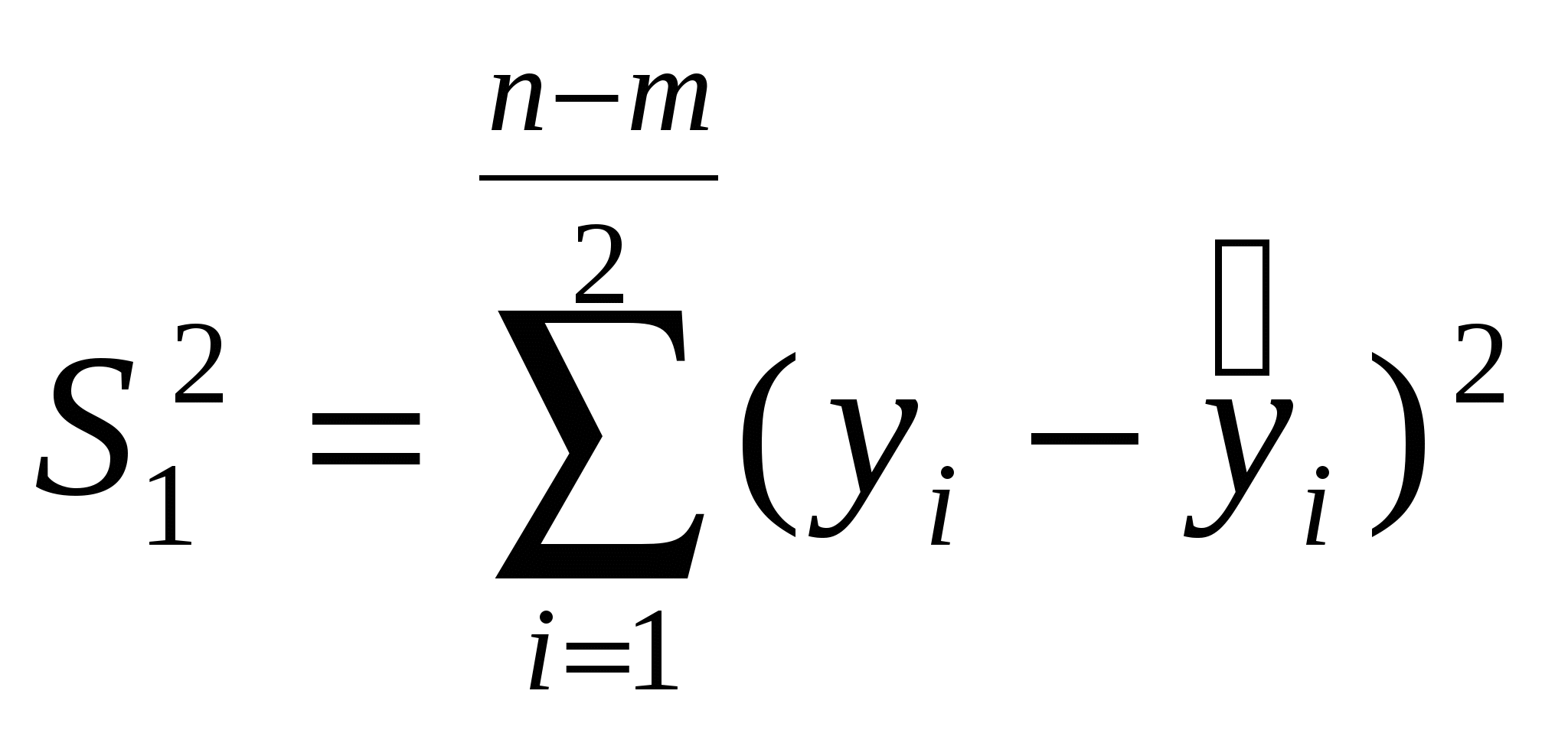 — для первой выборки и
— для первой выборки и 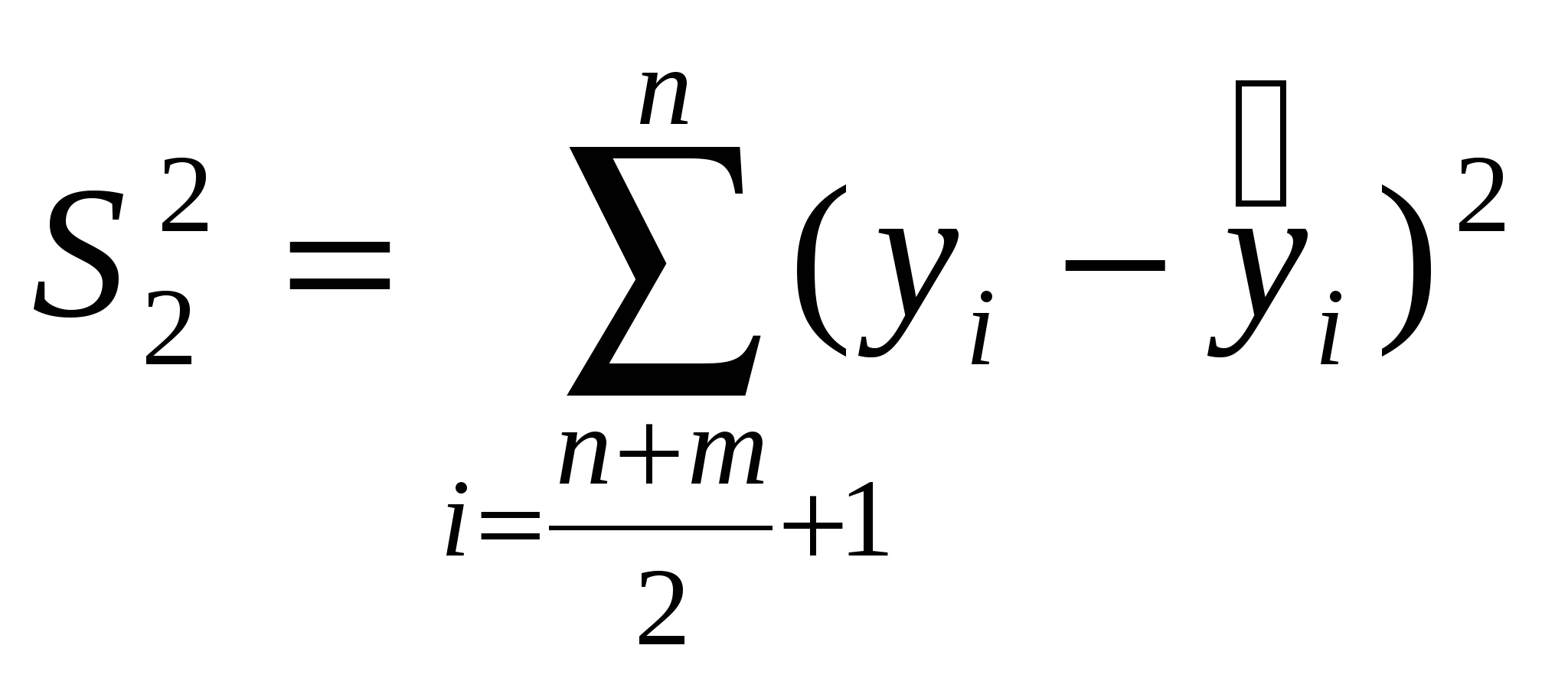 — для второй выборки;
— для второй выборки;