35 Моделирование тенденции временного ряда. 35 Моделирование тенденции временного ряда
 Скачать 1.88 Mb. Скачать 1.88 Mb.
|
Анализ временных рядовАна́лиз временны́х рядо́в — совокупность математико-статистических методов анализа, предназначенных для выявления структуры временных рядов и для их прогнозирования. Сюда относятся, в частности, методы регрессионного анализа. Выявление структуры временного ряда необходимо для того, чтобы построить математическую модель того явления, которое является источником анализируемого временного ряда. Прогноз будущих значений временного ряда используется для эффективного принятия решений. Пример временного ряда Временные ряды состоят из двух элементов:
Временные ряды классифицируются по следующим признакам:
Примеры временных рядовВременные ряды, как правило, возникают в результате измерения некоторого показателя. Это могут быть как показатели (характеристики) технических систем, так и показатели природных, социальных, экономических и других систем (например,погодные данные). Типичным примером временного ряда можно назвать биржевой курс, при анализе которого пытаются определить основное направление развития (тенденцию или тренда). 31 Автокорреляция уровней временного ряда и выявление его структуры При наличии во временном ряде тенденции и циклических колебаний значения каждого последующего уровня ряда зависят от предыдущих. Корреляционную зависимость между последовательными уровнями временного ряда называют автокорреляцией уровней ряда. Количественно её можно измерить с помощью линейного коэффициента корреляции между уровнями исходного временного ряда и уровнями этого ряда, сдвинутыми на несколько шагов во времени. Одна из рабочих формул для расчёта коэффициента автокорреляции имеет вид: 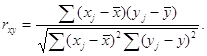 (1.2.1) (1.2.1)В качестве переменной х мы рассмотрим ряд y2, y3, … , yn; в качестве переменной у – ряд y1, y2, . . . ,yn– 1 . Тогда приведённая выше формула примет вид: 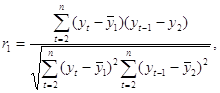 (1.2.2) (1.2.2)где 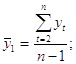 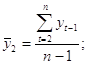 Аналогично можно определить коэффициенты автокорреляции второго и более высоких порядков. Так, коэффициент автокорреляции второго порядка характеризует тесноту связи между уровнями уt и yt – 1 и определяется по формуле 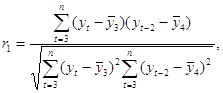 (1.2.3) (1.2.3)где 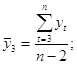 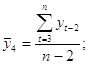 Число периодов, по которым рассчитывается коэффициент автокорреляции, называют лагом. С увеличением лага число пар значений, по которым рассчитывается коэффициент автокорреляции, уменьшается. Некоторые авторы считают целесообразным для обеспечения статистической достоверности коэффициентов автокорреляции использовать правило – максимальный лаг должен быть не больше (n/4). Отметим два важных свойства коэффициента автокорреляции. Во-первых, он строится по аналогии с линейным коэффициентом корреляции и таким образом характеризует тесноту только линейной связи текущего и предыдущего уровней ряда. Поэтому по коэффициенту автокорреляции можно судить о наличии линейной (или близкой к линейной) тенденции. Для некоторых временных рядов, имеющих сильную нелинейную тенденцию (например, параболу второго порядка или экспоненту), коэффициент автокорреляции уровней исходного ряда может приближаться к нулю. Во-вторых,по знаку коэффициента автокорреляции нельзя делать вывод о возрастающей или убывающей тенденции в уровнях ряда. Большинство временных рядов экономических данных содержит положительную автокорреляцию уровней, однако при этом могут иметь убывающую тенденцию. Последовательность коэффициентов автокорреляции уровней первого, второго и т. д. Порядков называют автокорреляционной функцией временного ряда. График зависимости её значений от величины лага (порядка коэффициента корреляции) называется коррелограммой. Анализ автокорреляционной функции и коррелограммы позволяет определить лаг, при котором автокорреляция наиболее высокая, а, следовательно, и лаг, при котором связь между текущим и предыдущими уровнями ряда наиболее тесная, то есть при помощи анализа автокорреляционной функции и коррелограммы можно выявить структуру ряда. Если наиболее высоким оказался коэффициент автокорреляции первого порядка, исследуемый ряд содержит только тенденцию. Если наиболее высоким оказался коэффициент автокорреляции порядка τ, ряд содержит циклические колебания с периодичностью в τ моментов времени. Если ни один из коэффициентов автокорреляции не является значимым, можно сделать одно из двух предположений относительно структуры этого ряда: либо ряд не содержит тенденции и циклических колебаний, либо ряд содержит сильную нелинейную тенденцию, для выявления которой нужно провести дополнительный анализ. Поэтому коэффициент автокорреляции уровней и автокорреляционную функцию целесообразно использовать для выявления во временном ряде наличия или отсутствия трендовой компоненты и циклической, сезонной компоненты. 30 Основные элементы временного ряда В каждом временном ряду имеются два основных элемента: время t и конкретное значение показателя (уровень ряда) у. Уровни ряда – это показатели, числовые значения которых составляют динамический ряд, т.е. они отображают количественную оценку (меру) развития во времени изучаемого явления. Время – это моменты или периоды, к которым относятся уровни2. Ряды динамики, как правило, представляют в виде таблицы или графика. Построение и анализ рядов динамики позволяют выявить и измерить закономерности развития общественных явлений во времени. Эти закономерности не проявляются четко на каждом конкретном уровне, а лишь в тенденции, в достаточно длительной динамике. На основную закономерность динамики накладываются другие, прежде всего случайные, иногда сезонные влияния. Выявление основной тенденции в изменении уровней, именуемой трендом, является одной из главных задач анализа рядов динамики. Основные задачи статистического изучения временных рядов При изучении динамики общественных явлений статистика решает ряд задач, чтобы дать числовую характеристику особенностей и закономерностей их развития на отдельных этапах: измеряет абсолютную и относительную скорость роста либо снижения уровня за отдельные промежутки времени; дает обобщающие характеристики уровня и скорости его изменения за тот или иной период; выявляет и численно характеризует основные тенденции развития явлений на отдельных этапах; дает сравнительную числовую характеристику развития данного явления в разных регионах или на разных этапах; выявляет факторы, обусловливающие изменение изучаемого явления во времени; делает прогнозы развития явления в будущем (экстраполяция и интерполяция). 29Обобщенный метод наименьших квадратов (ОМНК) При нарушении гомоскедастичности и наличии автокорреляции ошибок рекомендуется традиционный метод наименьших квадратов (известный в английской терминологии как метод OLS – Ordinary Least Squares) заменять обобщенным методом, т.е. методом GLS (Generalized Least Squares). Обобщенный метод наименьших квадратов применяется к преобразованным данным и позволяет получать оценки, которые обладают не только свойством несмещенности, но и имеют меньшие выборочные дисперсии. Остановимся на использовании ОМНК для корректировки гетероскедастичности. Как и раньше, будем предполагать, что среднее значение остаточных величин равно нулю. А вот дисперсия их не остается неизменной для разных значений фактора, а пропорциональна величине i K , т.е. 72 2 2 i Ki , где 2 i – дисперсия ошибки при конкретном i -м значении фактора; 2 – постоянная дисперсия ошибки при соблюдении предпосылки о гомоскедастичности остатков; i K – коэффициент пропорциональности, меняющийся с изменением величины фактора, что и обусловливает неоднородность дисперсии. При этом предполагается, что 2 неизвестна, а в отношении величин i K выдвигаются определенные гипотезы, характеризующие структуру гетероскедастичности. В общем виде для уравнения i i i y a bx при 2 2 i i K модель примет вид: i i i i y a bx K . В ней остаточные величины гетероскедастичны. Предполагая в них отсутствие автокорреляции, можно перейти к уравнению с гомоскедастичными остатками, поделив все переменные, зафиксированные в ходе i -го наблюдения, на i K . Тогда дисперсия остатков будет величиной постоянной, т. е. 2 2 i . Иными словами, от регрессии y по x мы перейдем к регрессии на новых переменных: y K и x K . Уравнение регрессии примет вид: i i i i i i y a x b K K K , а исходные данные для данного уравнения будут иметь вид: 73 1 1 2 2 ........ n n y K y y K y K , 1 1 2 2 ........ n n x K x x K x K . По отношению к обычной регрессии уравнение с новыми, преобразованными переменными представляет собой взвешенную регрессию, в которой переменные y и x взяты с весами 1 K . Оценка параметров нового уравнения с преобразованными переменными приводит к взвешенному методу наименьших квадратов, для которого необходимо минимизировать сумму квадратов отклонений вида 2 1 1 , n i i i i S a b y a bx K Σ . Соответственно получим следующую систему нормальных уравнений: 2 1 , . y x a b K K K y x x x a b K K K Σ Σ Σ Σ Σ Σ Если преобразованные переменные x и y взять в отклонениях от средних уровней, то коэффициент регрессии b можно определить как 2 1 1 x y b K x K Σ Σ . При обычном применении метода наименьших квадратов к уравнению линейной регрессии для переменных в отклонениях от средних уровней коэффициент регрессии b определяется по формуле: 74 2 x y b x Σ Σ . Как видим, при использовании обобщенного МНК с целью корректировки гетероскедастичности коэффициент регрессии b представляет собой взвешенную величину по отношению к обычному МНК с весом 1 K . Аналогичный подход возможен не только для уравнения парной, но и для множественной регрессии. Предположим, что рассматривается модель вида y a b1x1 b2x2 , для которой дисперсия остаточных величин оказалась пропорциональна 2 i K . i K представляет собой коэффициент пропорциональности, принимающий различные значения для соответствующих i значений факторов 1 x и 2 x . Ввиду того, что 2 2 2 i i K , рассматриваемая модель примет вид i 1 1i 2 2i i i y a b x b x K, где ошибки гетероскедастичны. Для того чтобы получить уравнение, где остатки i гомоскедастичны, перейдем к новым преобразованным переменным, разделив все члены исходного уравнения на коэффициент пропорциональности K . Уравнение с преобразованными переменными составит 1 2 1 2 i i i i i i i i y a x x b b K K K K . Это уравнение не содержит свободного члена. Вместе с тем, найдя переменные в новом преобразованном виде и применяя обычный МНК к ним, получим иную спецификацию модели: 75 1 2 1 2 i i i i i i i y x x A b b K K K . Параметры такой модели зависят от концепции, принятой для коэффициента пропорциональности i K . В эконометрических исследованиях довольно часто выдвигается гипотеза, что остатки i пропорциональны значениям фактора. Так, если в уравнении 1 1 2 2 ... m m y a b x b x b x e предположить, что 1 e x , т.е. 1 K x и 2 2 i 1 x , то обобщенный МНК предполагает оценку параметров следующего трансформированного уравнения: 2 1 2 1 1 1 ... m m y x x b b b x x x . Применение в этом случае обобщенного МНК приводит к тому, что наблюдения с меньшими значениями преобразованных переменных x K имеют при определении параметров регрессии относительно больший вес, чем с первоначальными переменными. Вместе с тем, следует иметь в виду, что новые преобразованные переменные получают новое экономическое содержание и их регрессия имеет иной смысл, чем регрессия по исходным данным. Пример. Пусть y – издержки производства, 1 x – объем продукции, 2 x – основные производственные фонды, 3 x – численность работников, тогда уравнение 1 1 2 2 3 3 y a b x b x b x e является моделью издержек производства с объемными факторами. Предполагая, что 2 i пропорциональна квадрату численности работников 3 x , мы получим в качестве результативного признака затраты на одного работника 3 y x , а в качестве факторов следующие показатели: 76 производительность труда 1 3 x x и фондовооруженность труда 2 3 x x . Соответственно трансформированная модель примет вид 1 2 3 1 2 3 3 3 y x x b b b x x x , где параметры 1 b , 2 b , 3 b численно не совпадают с аналогичными параметрами предыдущей модели. Кроме этого, коэффициенты регрессии меняют экономическое содержание: из показателей силы связи, характеризующих среднее абсолютное изменение издержек производства с изменением абсолютной величины соответствующего фактора на единицу, они фиксируют при обобщенном МНК среднее изменение затрат на работника; с изменением производительности труда на единицу при неизменном уровне фовдовооруженности труда; и с изменением фондовооруженности труда на единицу при неизменном уровне производительности труда. Если предположить, что в модели с первоначальными переменными дисперсия остатков пропорциональна квадрату объема продукции, 2 2 2 i 1 x , можно перейти к уравнению регрессии вида 2 3 1 2 3 1 1 1 y x x b b b x x x . В нем новые переменные: 1 y x – затраты на единицу (или на 1 руб. продукции), 2 1 x x – фондоемкость продукции, 3 1 x x – трудоемкость продукции. Гипотеза о пропорциональности остатков величине фактора может иметь реальное основание: при обработке недостаточно однородной совокупности, включающей как крупные, так и мелкие предприятия, большим объемным значениям фактора может соответствовать большая дисперсия результативного признака и большая дисперсия остаточных величин. 77 При наличии одной объясняющей переменной гипотеза 2 2 2 i x трансформирует линейное уравнение y a bx e в уравнение y a b x x , в котором параметры a и b поменялись местами, константа стала коэффициентом наклона линии регрессии, а коэффициент регрессии – свободным членом. Пример. Рассматривая зависимость сбережений y от дохода x , по первоначальным данным было получено уравнение регрессии y 1,0810,1178x. Применяя обобщенный МНК к данной модели в предположении, что ошибки пропорциональны доходу, было получено уравнение для преобразованных данных: 1 0,1026 0,8538 y x x . Коэффициент регрессии первого уравнения сравнивают со свободным членом второго уравнения, т.е. 0,1178 и 0,1026 – оценки параметра b зависимости сбережений от дохода. Переход к относительным величинам существенно снижает вариацию фактора и соответственно уменьшает дисперсию ошибки. Он представляет собой наиболее простой случай учета гетероскедастичности в регрессионных моделях с помощью обобщенного МНК. Процесс перехода к относительным величинам может быть осложнен выдвижением иных гипотез о пропорциональности ошибок относительно включенных в модель факторов. Использование той или иной гипотезы предполагает специальные исследования остаточных величин для соответствующих регрессионных 78 моделей. Применение обобщенного МНК позволяет получить оценки параметров модели, обладающие меньшей дисперсией. 28 |
