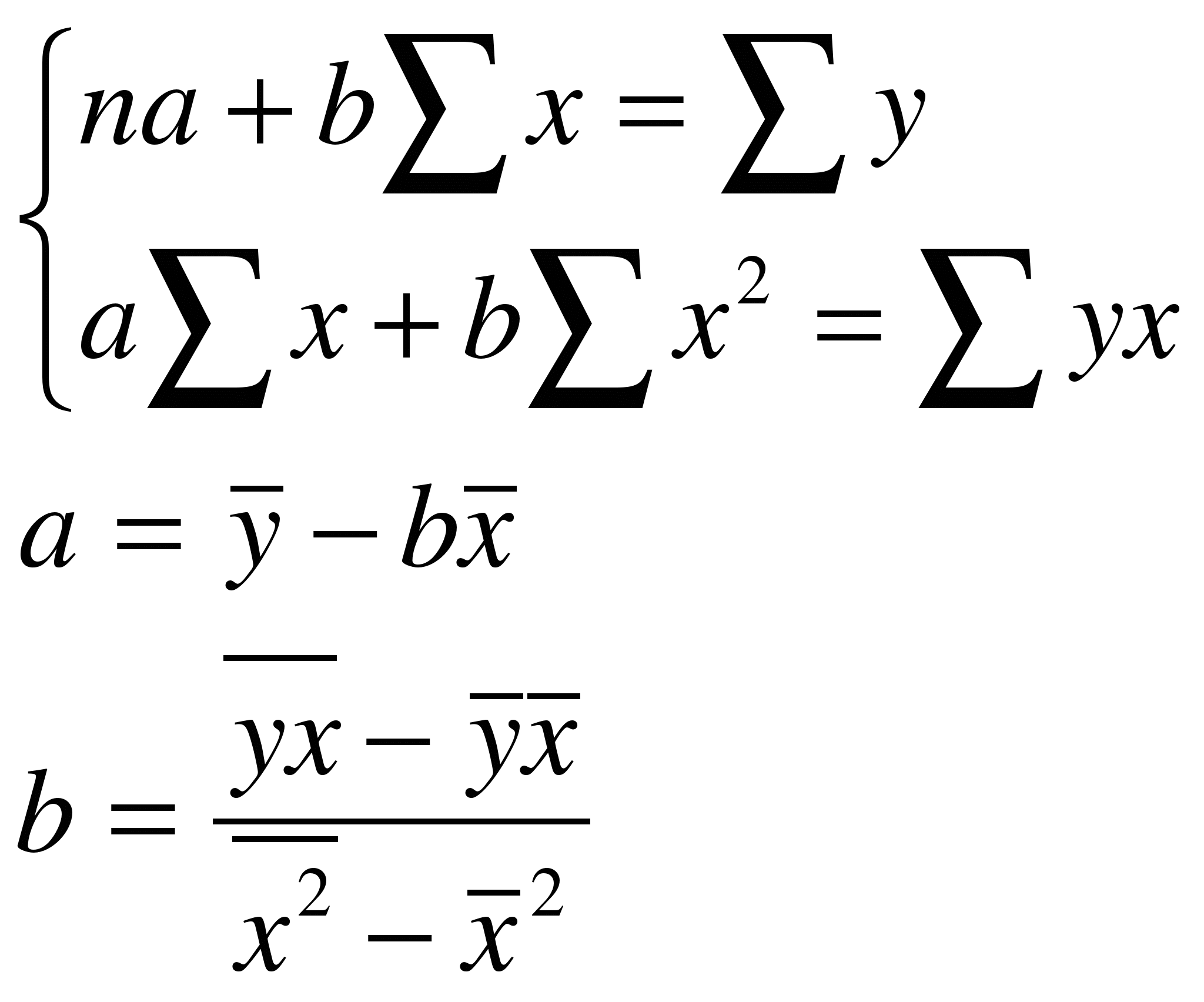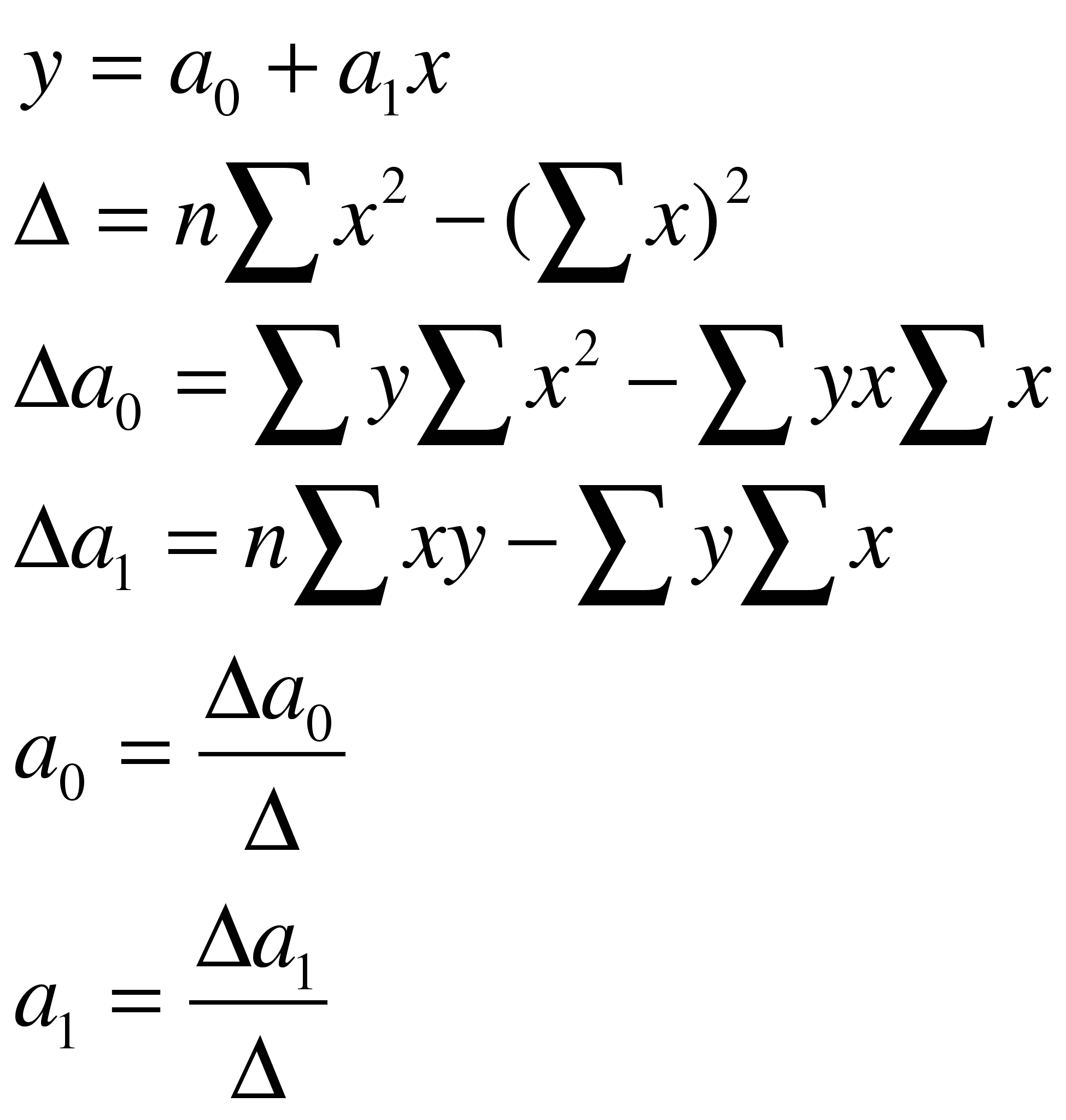35 Моделирование тенденции временного ряда. 35 Моделирование тенденции временного ряда
 Скачать 1.88 Mb. Скачать 1.88 Mb.
|
10 Интервалы прогноза по линейному уравнению регрессииОценка статистической значимости параметров регрессии проводится с помощью t-статистики Стьюдента и путем расчета доверительного интервала для каждого из показателей. Выдвигается гипотеза Н0 о статистически значимом отличие показателей от 0 a = b = r = 0. Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что параметры a и b находясь в указанных границах не принимают нулевых значений, т.е. не является статистически незначимыми и существенно отличается от 0.9 Оценка значимости коэффициентов регрессии и корреляции с помощью f-критерия Стьюдента Необходимость применения многофакторного корреляционного анализа. Этапы многофакторного корреляционного анализа. Правила отбора факторов для корреляционной модели. Обоснование необходимого объема выборки данных для корреляционного анализа. Сбор и статистическая оценка исходной информации. Способы обоснования уравнения связи. Основные показатели связи в корреляционном анализе и их интерпретация. Сущность парных (общих), частных и множественных коэффициентов корреляции и детерминации. Оценка значимости коэффициентов корреляции. Порядок расчета уравнения множественной регрессии шаговым способом. Интерпретация его параметров. Назначение коэффициентов эластичности и стандартизированных бетта-коэф-фициентов. [1] После построения уравнения регрессии необходимо сделать проверку его значимости: с помощью специальных критериев установить, не является ли полученная зависимость, выраженная уравнением регрессии, случайной, т.е. можно ли ее использовать в прогнозных целях и для факторного анализа. В статистике разработаны методики строгой проверки значимости коэффициентов регрессии с помощью дисперсионного анализа и расчета специальных критериев (например, F-критерия). Нестрогая проверка может быть выполнена путем расчета среднего относительного линейного отклонения (ё), называемого средней ошибкой аппроксимации: Перейдем теперь к оценке значимости коэффициентов регрессии bj и построению доверительного интервала для параметров регрессионной модели Ру (J=l,2,..., р). Блок 5 - оценка значимости коэффициентов регрессий по величине ^-критерия Стьюдента. Расчетные значения ta сравниваются с допустимым значением Блок 5 - оценка значимости коэффициентов регрессий по величине ^-критерия. Расчетные значения t0n сравниваются с допустимым значением 4,/, которое определяется по таблицам t - распределения для заданной вероятности ошибок (а) и числа степеней свободы (/). Кроме проверки значимости всей модели, необходимо провести проверки значимости коэффициентов регрессии по /-критерию Стюдента. Минимальное значение коэффициента регрессии Ьг должно соответствовать условию bifob- ^t, где bi - значение коэффициента уравнения регрессии в натуральном масштабе при i-ц факторном признаке; аь. - средняя квадратическая ошибка каждого коэффициента. несопоставимость между собой по своей значимости коэффициентов D; Дальнейший статистический анализ касается проверки значимости коэффициентов регрессии. Для этого находим значение ^-критерия для коэффициентов регрессии. В результате их сравнения определяется наименьший по величине ^-критерий. Фактор, коэффициенту которого соответствует наименьший ^-критерий, исключается из дальнейшего анализа. Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t-критерий Стъюдента и доверительные интервалы каждого из показателей. Выдвигается гипотеза Но о случайной природе показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью f-критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки: Оценка значимости коэффициентов чистой регрессии с помощью /-критерия Стьюдента сводится к вычислению значения Качество труда - характеристика конкретного труда, отражающая степень его сложности, напряженности (интенсивности), условия и значимость для развития экономики. К.т. измеряется посредством тарифной системы, позволяющей дифференцировать заработную плату в зависимости от уровня квалификации (сложности труда), условий, тяжести труда и его интенсивности, а также значимости отдельных отраслей и производств, районов, территорий для развития экономики страны. К.т. находит выражение в заработной плате работников, складывающейся на рынке труда под воздействием спроса и предложения рабочей силы (конкретные виды труда). К.т. - сложная по структуре Полученные баллы относительной значимости отдельных экономических, социальных и экологических последствий осуществления проекта дают далее основу для сравнения альтернативных проектов и их вариантов с помощью "комплексного балльного безразмерного критерия социальной и эколого-экономической эффективности" проекта Эк, рассчитываемого (в усредненных баллах значимости) по формуле Внутриотраслевое регулирование обеспечивает различия в оплате труда работников данной отрасли промышленности в зависимости от значимости отдельных .видов производства данной отрасли, от сложности и условий труда, а также от применяемых форм оплаты труда. Полученная рейтинговая оценка анализируемого предприятия по отношению к предприятию-эталону без учета значимости отдельных показателей является сравнительной. При сравнении рейтинговых оценок нескольких предприятий наивысший рейтинг имеет предприятие с минимальным значением полученной сравнительной оценки. Понимание качества товара как меры его полезности ставит практически важный вопрос об её измерении. Его решение достигается изучением значимости отдельных свойств в удовлетворении определенной потребности. Значимость даже одного и того же свойства может быть неодинаковой в зависимости от условий потребления продукта. Следовательно, и полезность товара в разных обстоятельствах её использования различна. Второй этап работы - изучение статистических данных и выявление взаимосвязи и взаимодействия показателей, определение значимости отдельных факторов и причин изменения общих показателей. [2] Все рассматриваемые показатели сводятся в один таким образом, что в результате получается комплексная оценка всех анализируемых сторон деятельности предприятия с учетом условий его деятельности, с учетом степени значимости отдельных показателей для различных типов инвесторов: Коэффициенты регрессии показывают интенсивность влияния факторов на результативный показатель. Если проведена предварительная стандартизация факторных показателей, то Ь0 равняется среднему значению результативного показателя в совокупности. Коэффициенты Ь,, Ь2 ..... Ьл показывают, на сколько единиц уровень результативного показателя отклоняется от своего среднего значения, если значения факторного показателя отклоняются от среднего, равного нулю, на одно стандартное отклонение. Таким образом, коэффициенты регрессии характеризуют степень значимости отдельных факторов для повышения уровня результативного показателя. Конкретные значения коэффициентов регрессии определяют по эмпирическим данным согласно методу наименьших квадратов (в результате решения систем нормальных уравнений). 8Оценка значимости параметров линейной регрессии. Оценка значимости уравнения регрессии в целом дается с помощью F-критерия Фишера. Показатель где ух – теоретическое значение переменной у вычисленное по полученному уравнению регрессии. Вычисленное значение Ф-критерия признается достоверным, если оно больше табличного. Если меньше, то найденное уравнение линейной регрессии считается статистически не значимым. Существует альтернативная формула для Ф-критерия: Оценка значимости коэффициента регрессии. Сначала найдем стандартную ошибку: 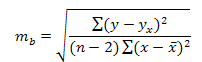 Затем находим значение Т-критерия Стьюдента по формуле t=b/mb. Затем находим значение Т-критерия Стьюдента по формуле t=b/mb.Найденное значение сравниваем с табличным при определенном уровне значимости и числе степеней свободы. Если больше табличного, то значение коэффициента регрессии статистически значимо. Для оценки качества построенной модели используют средний коэффициент эластичности, который показывает на сколько % в среднем по совокупности изменится результат от своей средней величины при изменении факторной переменной х на 1% от своего среднего значения. Э=(b*x среднее)/(y среднее)
6 ОЦЕНКА СУЩЕСТВЕННОСТИ ПАРАМЕТРОВЛИНЕЙНОЙ РЕГРЕССИИ И КОРРЕЛЯЦИИ. Оценка значимости уравнения регрессии в целом дается с помощью F-критерия Фишера. При этом выдвигается нулевая гипотеза, что коэффициент регрессии равен нулю, т. е. b=0, и следовательно, фактор хне оказывает влияния на результат у. Непосредственному расчету F-критерия предшествует анализ дисперсии. Центральное место в нем занимает разложение общей суммы квадратов отклонений переменной уот средне го значения уна две части - «объясненную» и «необъясненную»: 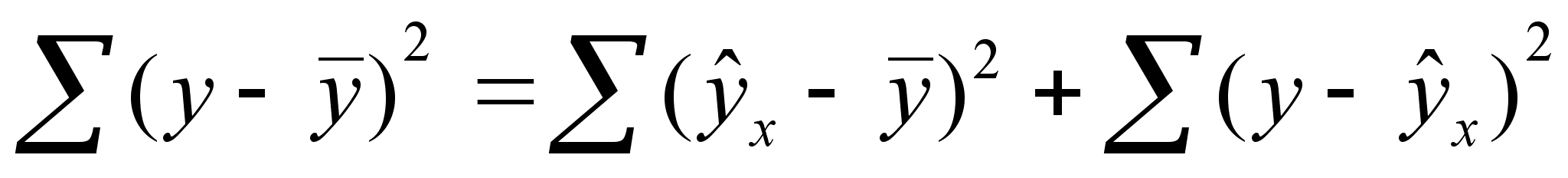 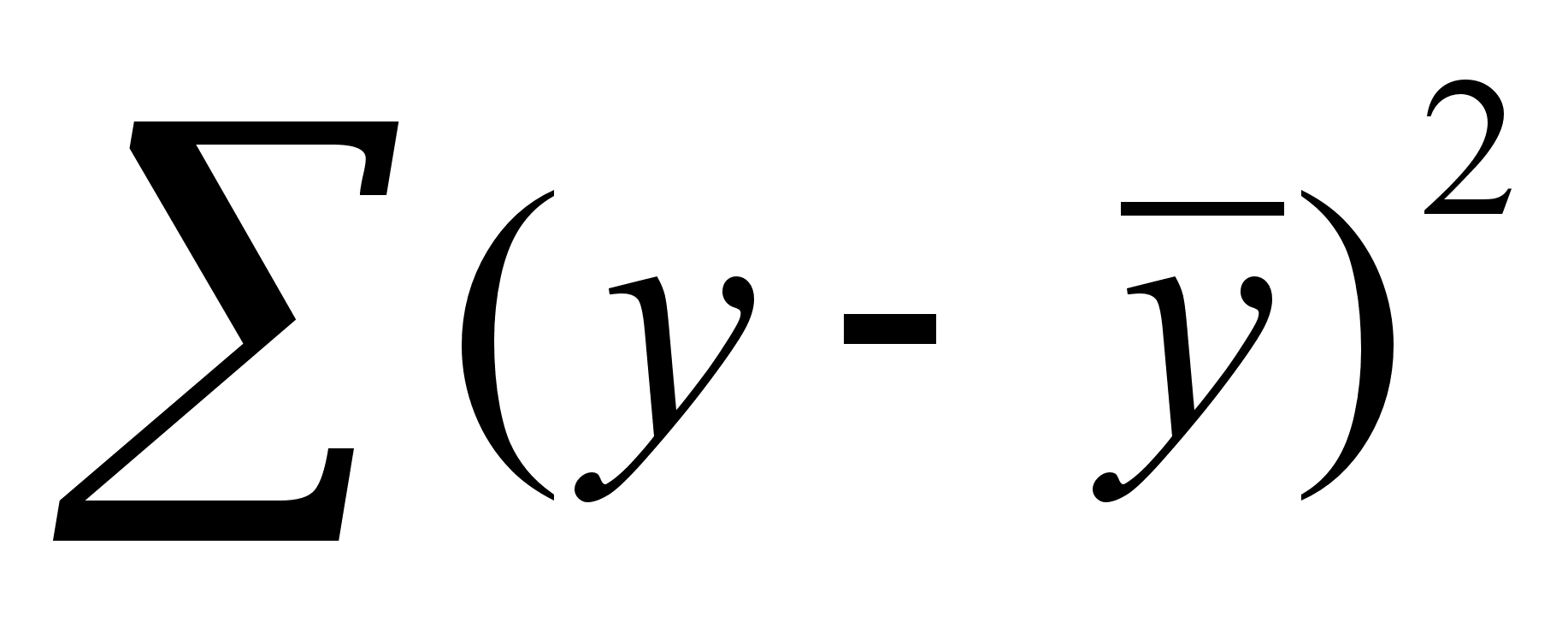 - общая сумма квадратов отклонений - общая сумма квадратов отклонений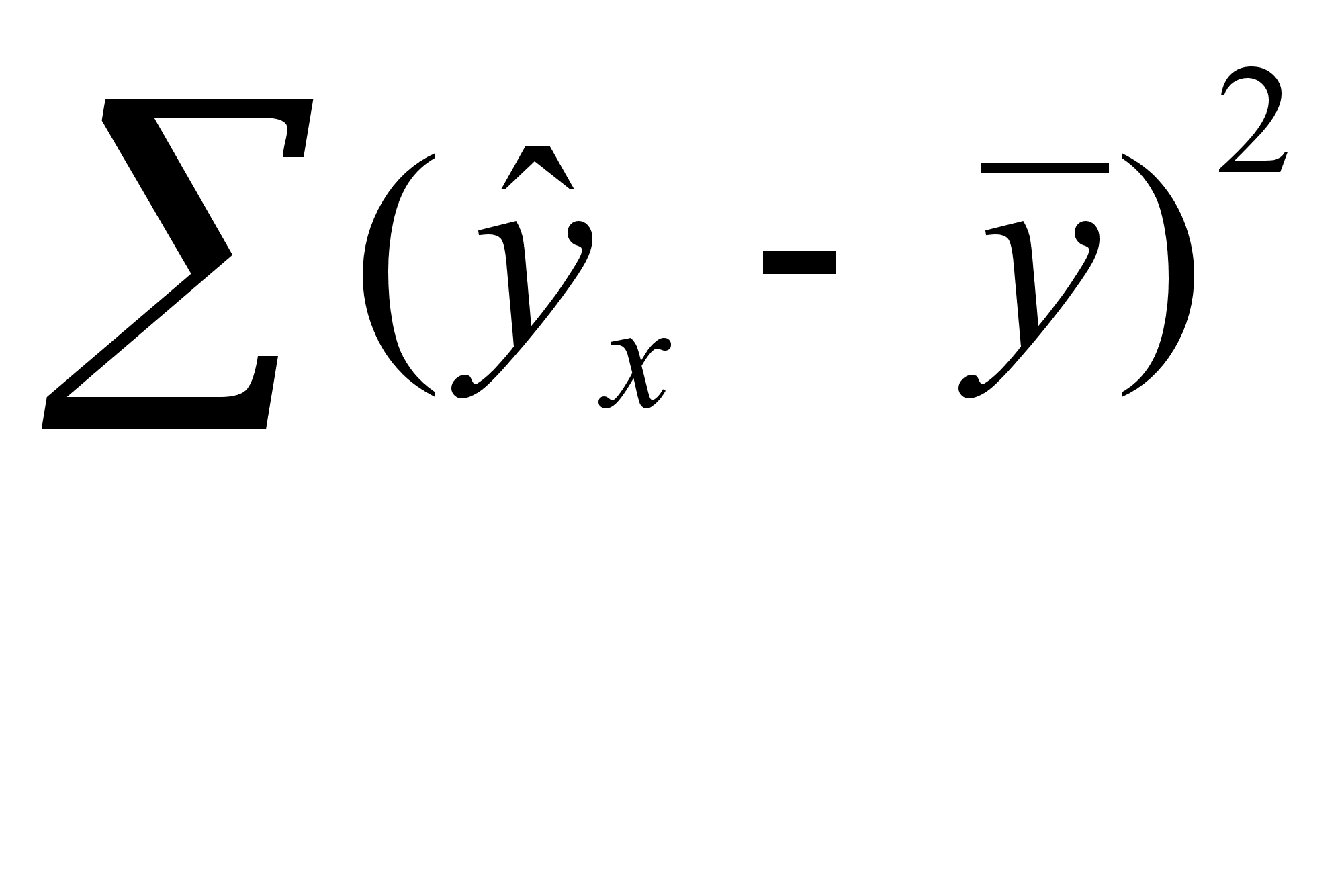 - сумма квадратов отклонения объясненная регрессией - сумма квадратов отклонения объясненная регрессией 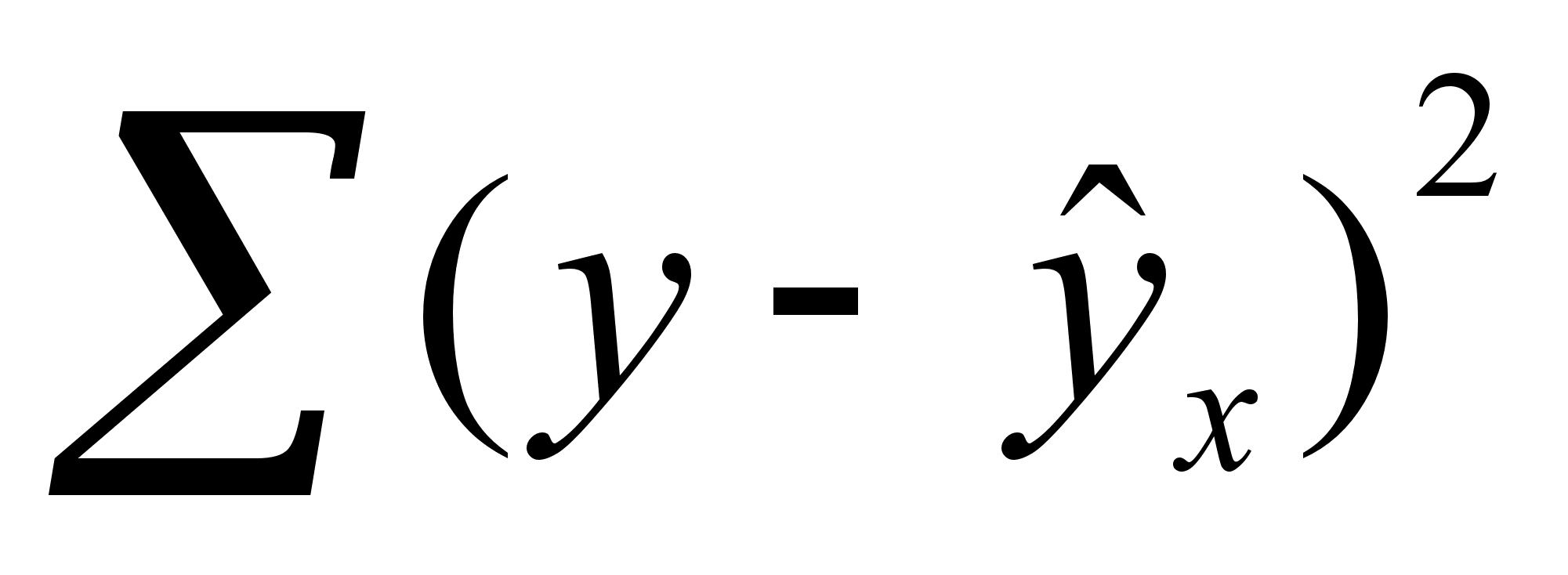 - остаточная сумма квадратов отклонения. - остаточная сумма квадратов отклонения.Любая сумма квадратов отклонений связана с числом степеней свободы,т. е. с числом свободы независимого варьирования признака. Число степеней свободы связано с числом единиц совокупности nис числом определяемых по ней констант. Применительно к исследуемой проблеме число cтепеней свободы должно показать, сколько независимых отклонений из пвозможных требуется для образования данной суммы квадратов. Дисперсия на одну степень свободыD. 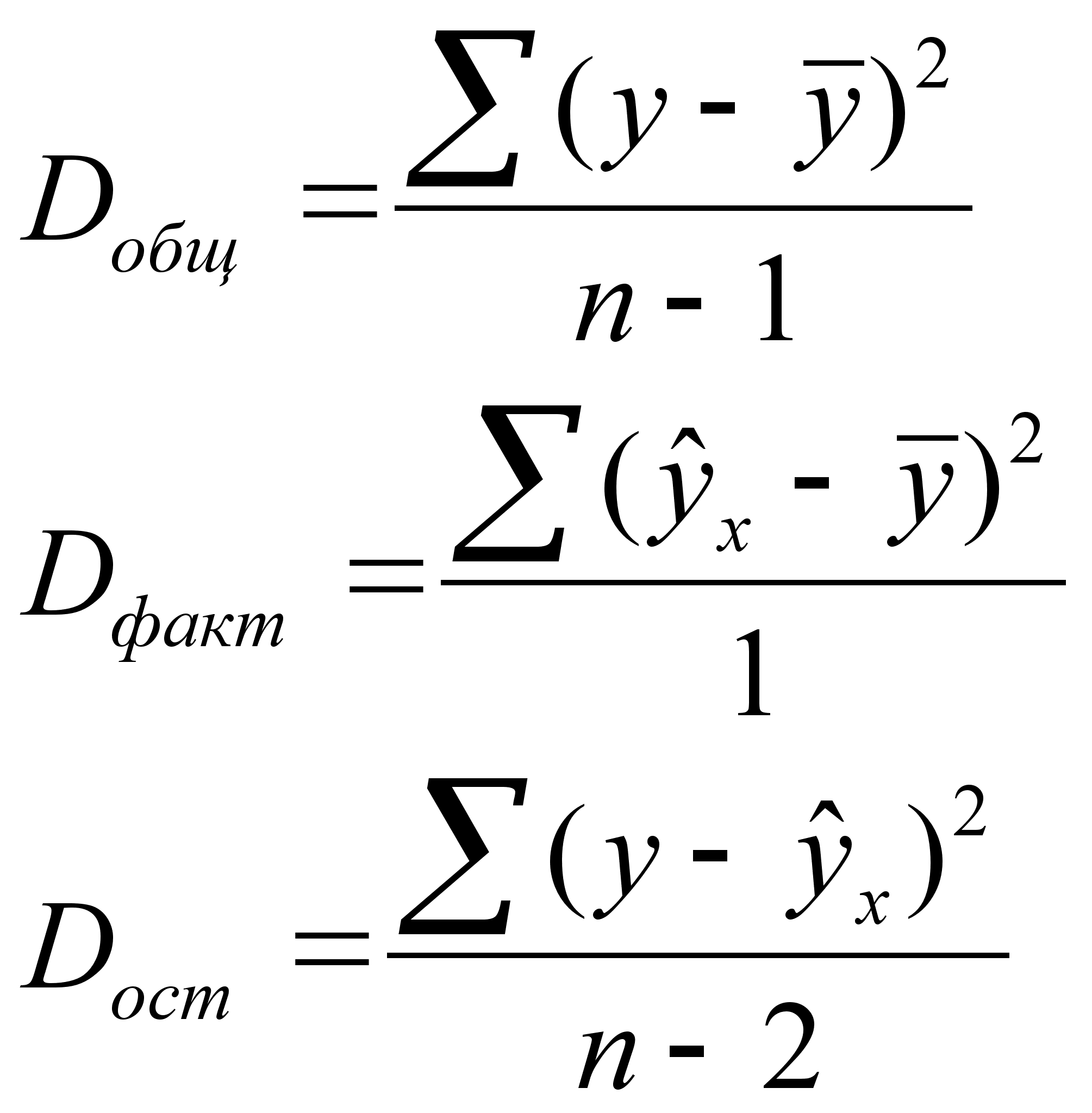 F-отношения (F-критерий): 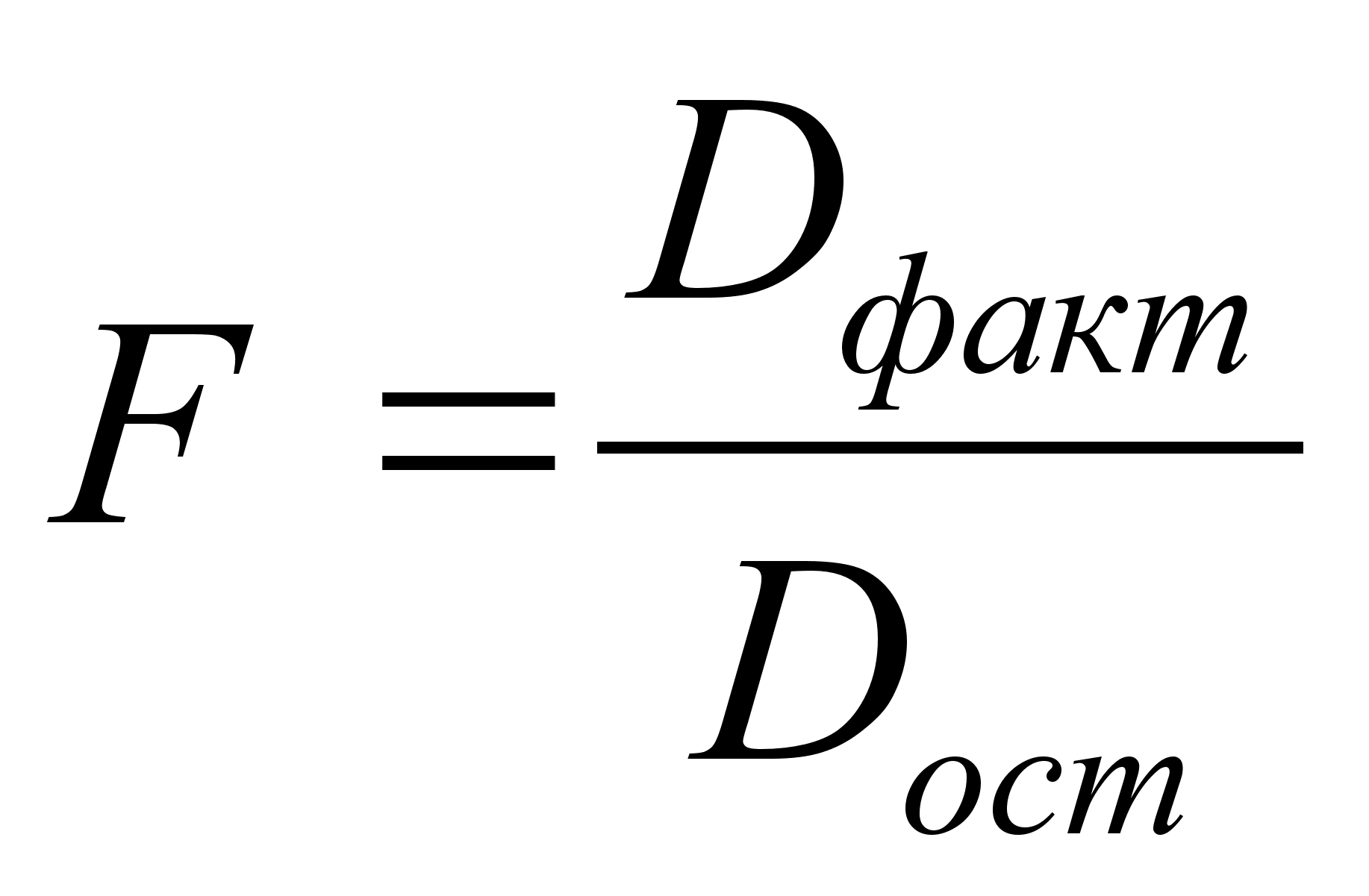 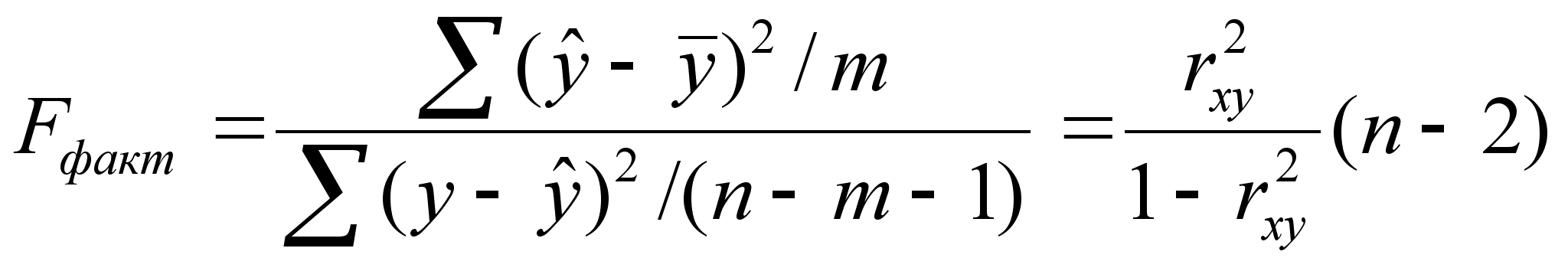 Ecли нулевая гипотеза справедлива, то факторная и остаточная дисперсии не отличаются друг от друга. Для Н0 необходимо опровержение,чтобы факторная дисперсия превышала остаточную в несколько раз. Английским статистиком Снедекором разработаны таблицы критических значений F-отношений при разных уровняхсущественности нулевой гипотезы и различном числе степенейсвободы. Табличное значение F-критерия — это максимальная величина отношения дисперсий, которая может иметь место прислучайном их расхождении для данного уровня вероятности наличия нулевой гипотезы. Вычисленное значение F-отношения признается достоверным, если о больше табличного. В этом случае нулевая гипотеза об отсутствии связи признаков отклоняется и делается вывод о существенности этой связи: Fфакт > Fтабл Н0 отклоняется. Если же величина окажется меньше табличной Fфакт ‹, Fтабл , то вероятность нулевой гипотезы выше заданного уровня и она не может быть отклонена без серьезного риска сделать неправильный вывод о наличии связи. В этом случае уравнение регрессии считается статистически незначимым. Но не отклоняется. Стандартная ошибка коэффициента регрессии 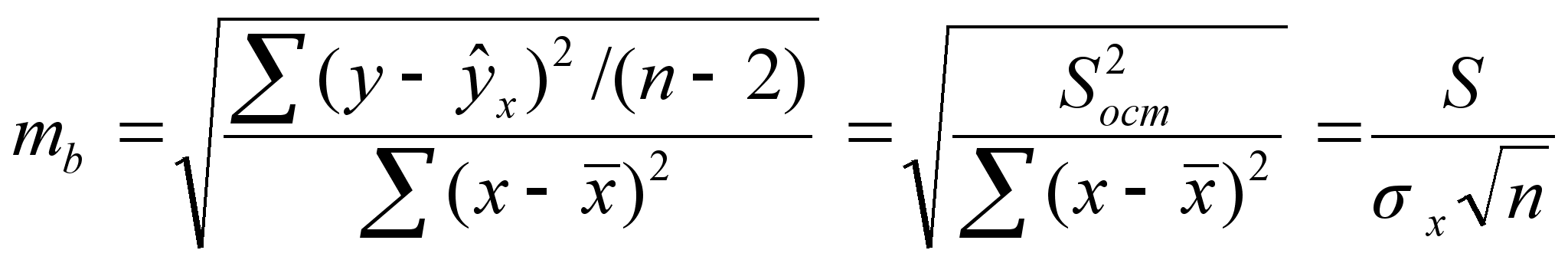 Для оценки существенности коэффициента регрессии его величина сравнивается с его стандартной ошибкой, т. е. определяется фактическое значение t-критерия Стьюдентa: 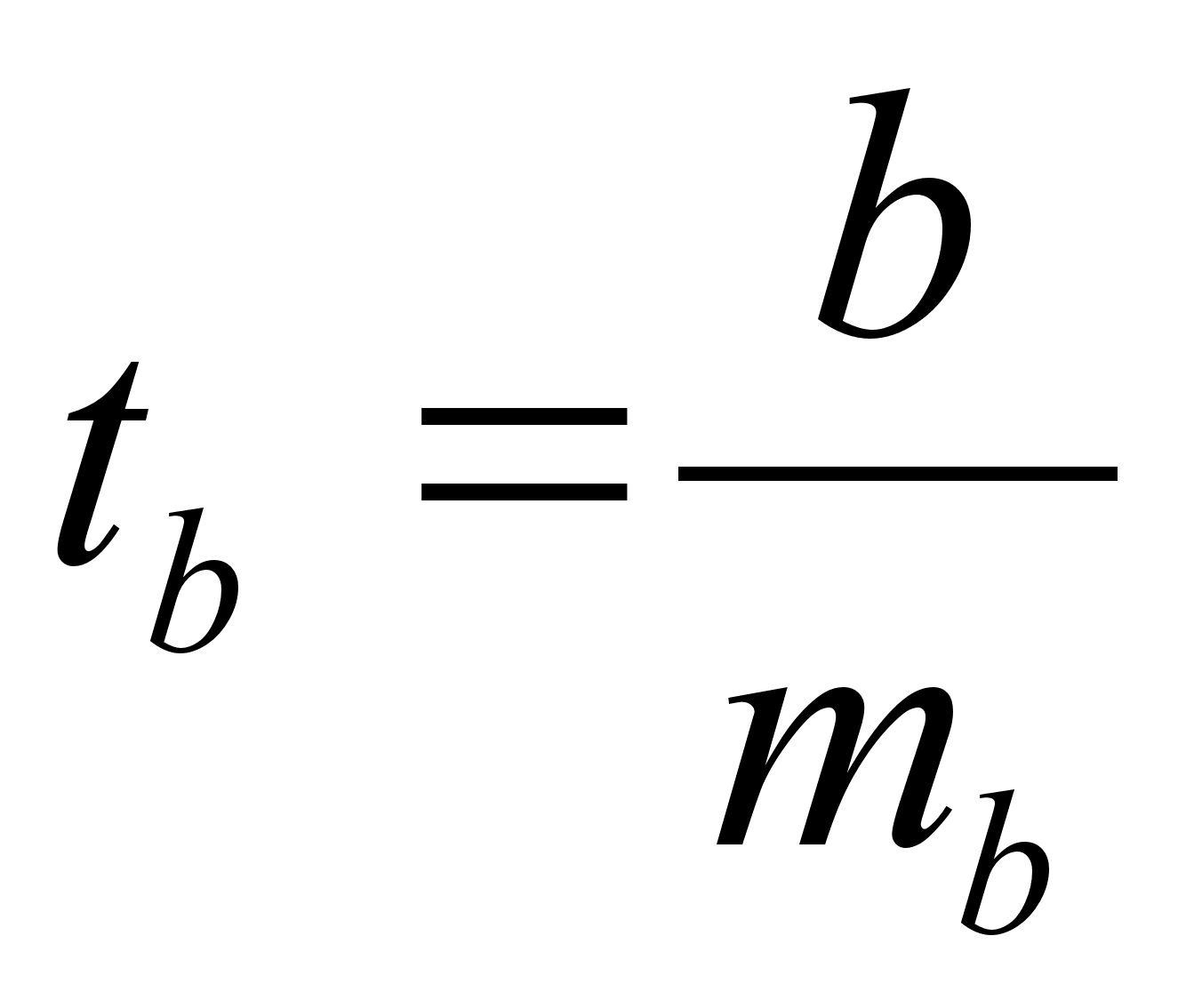 которое котороезатем сравнивается с табличным значением при определенном уровне значимости 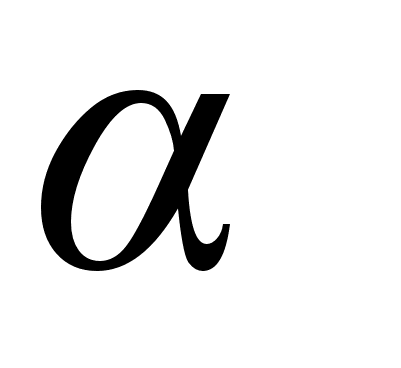 и числе степеней свободы (n- 2). и числе степеней свободы (n- 2).Стандартная ошибка параметра а: 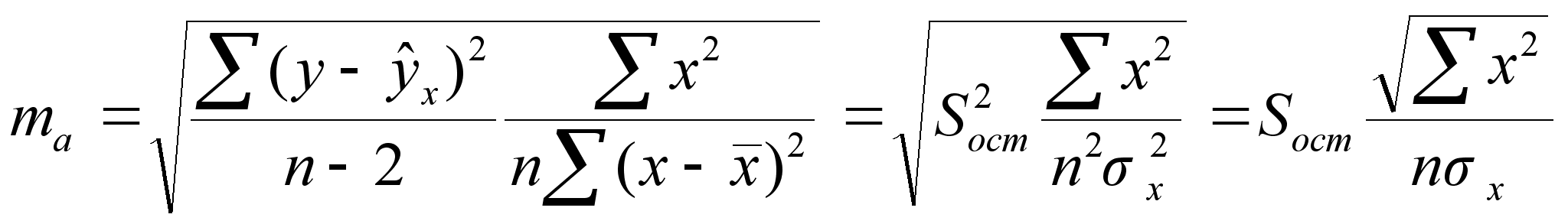 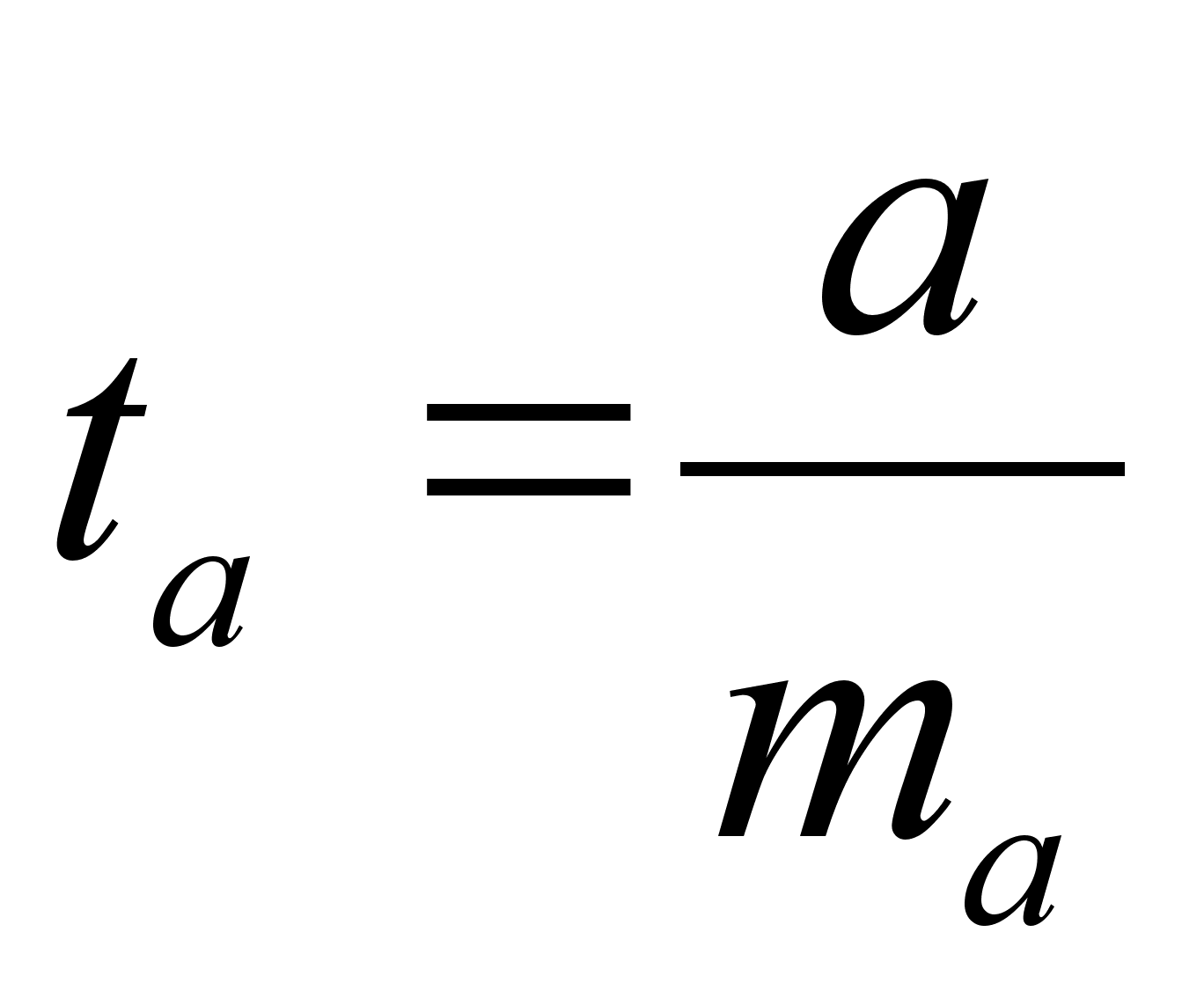 Значимость линейного коэффициента корреляции проверяется на основе величины ошибки коэффициента корреляции тr: 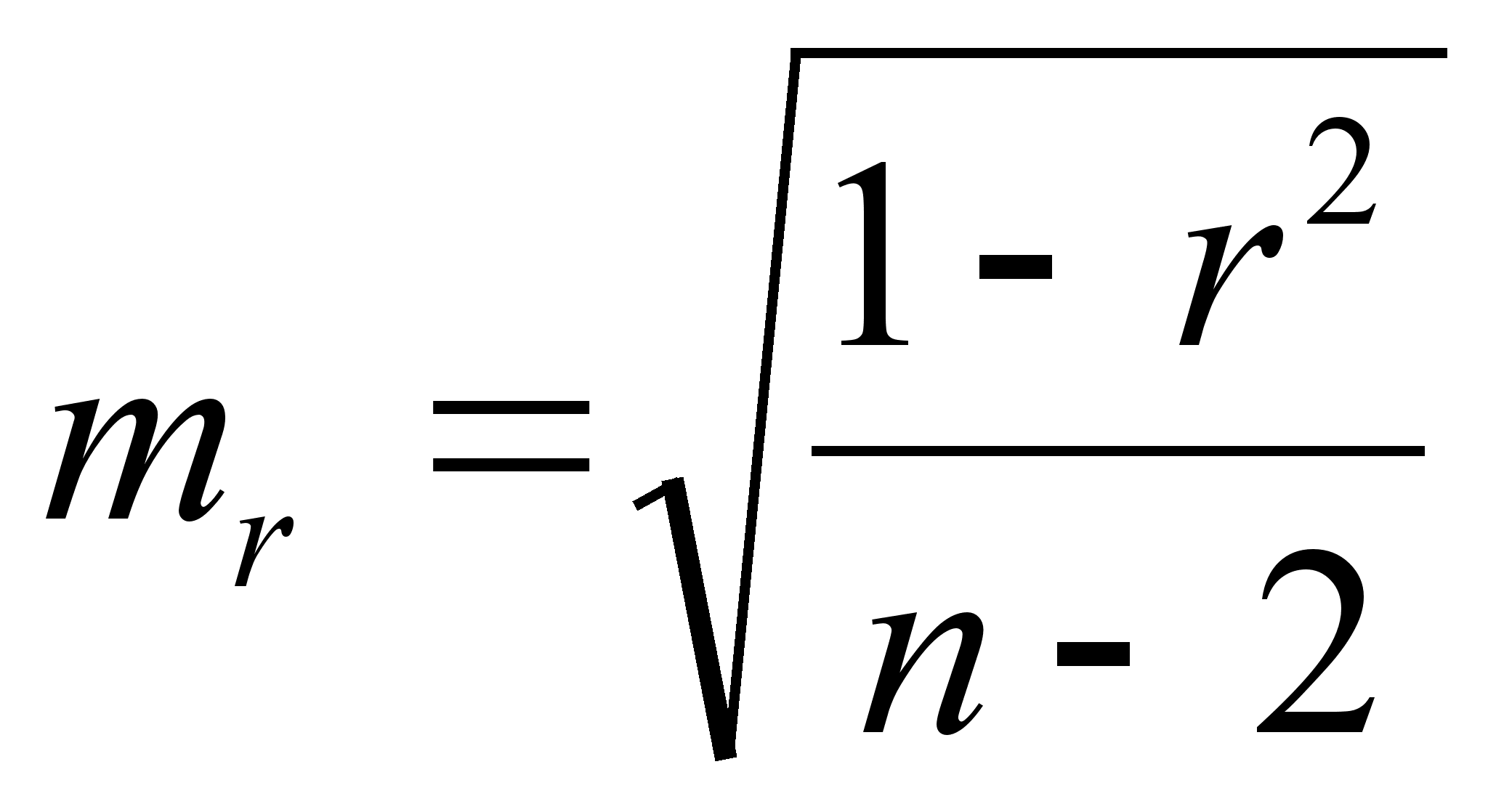 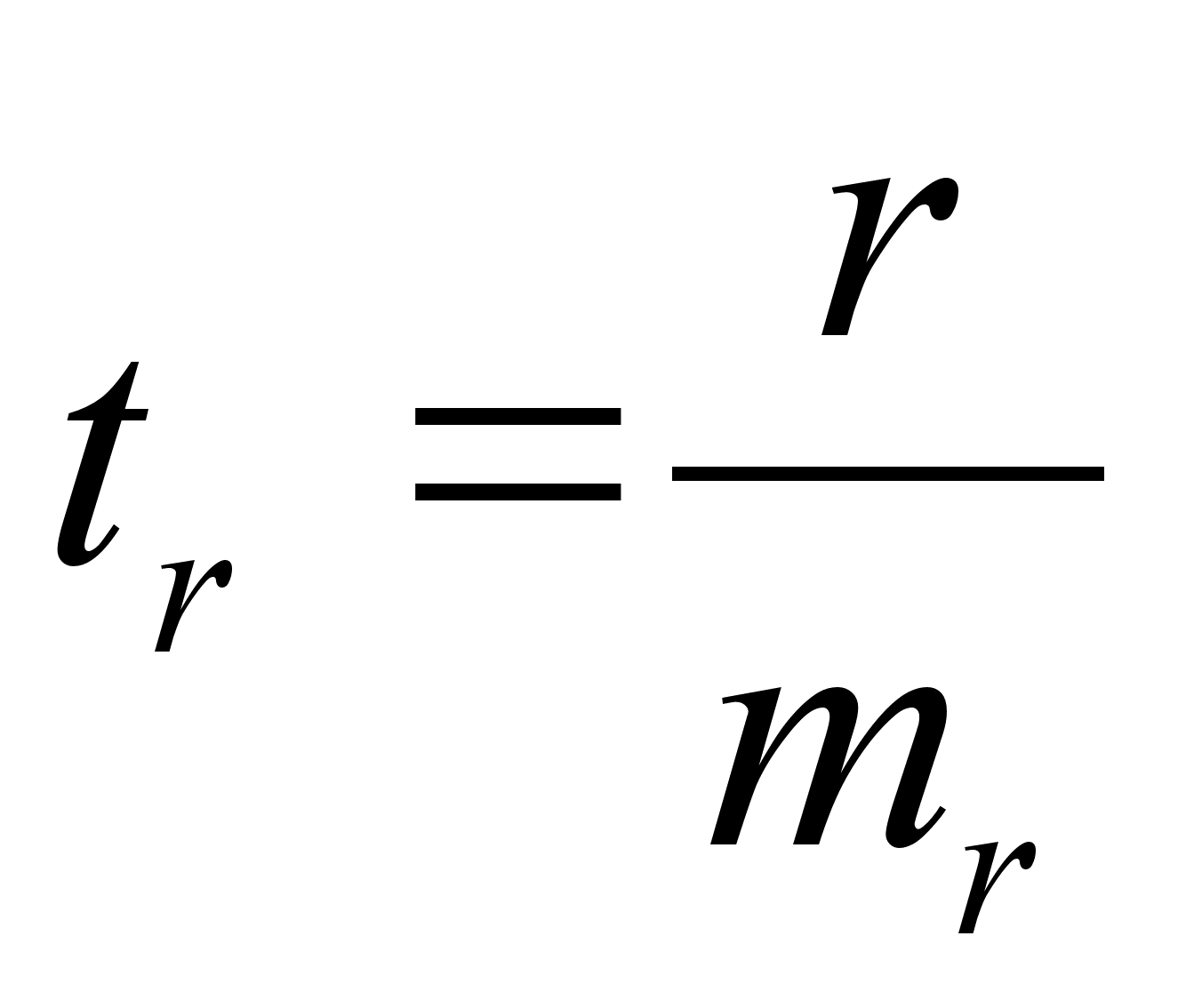 Общая дисперсия признака х: 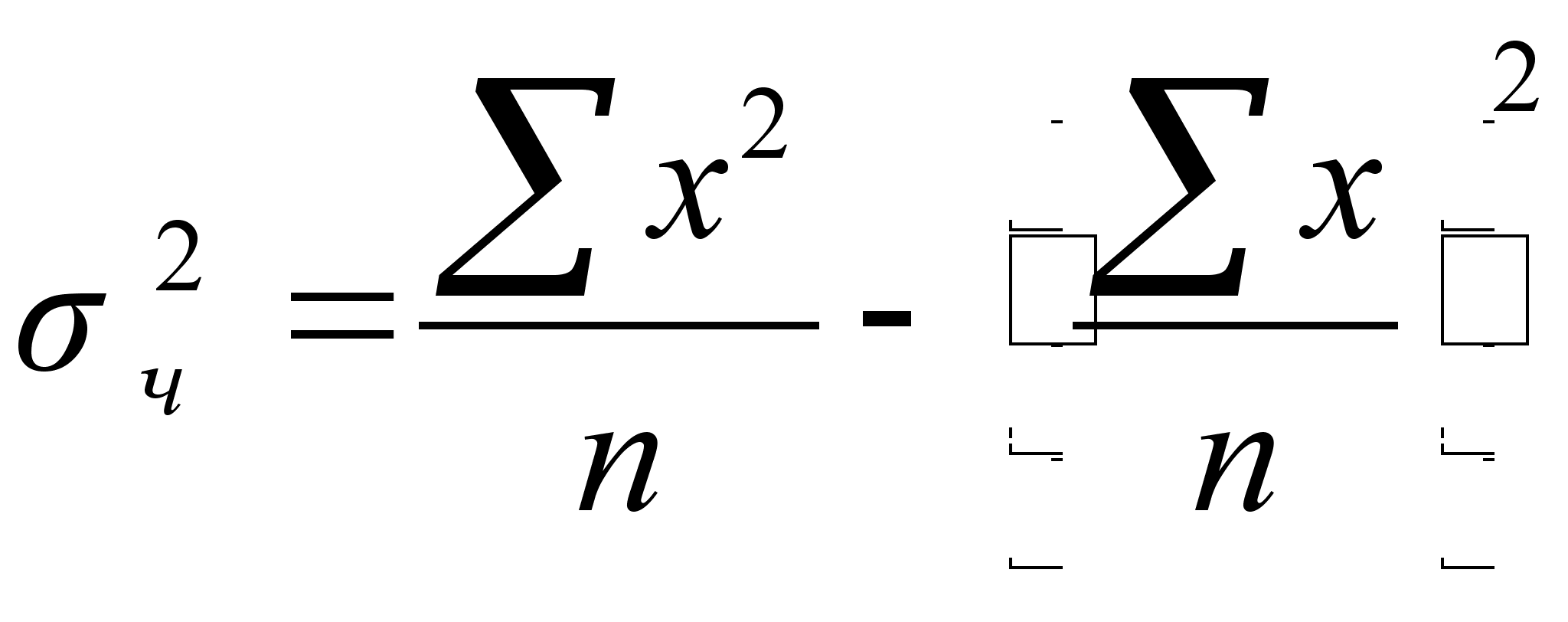 Коэф. регрессии 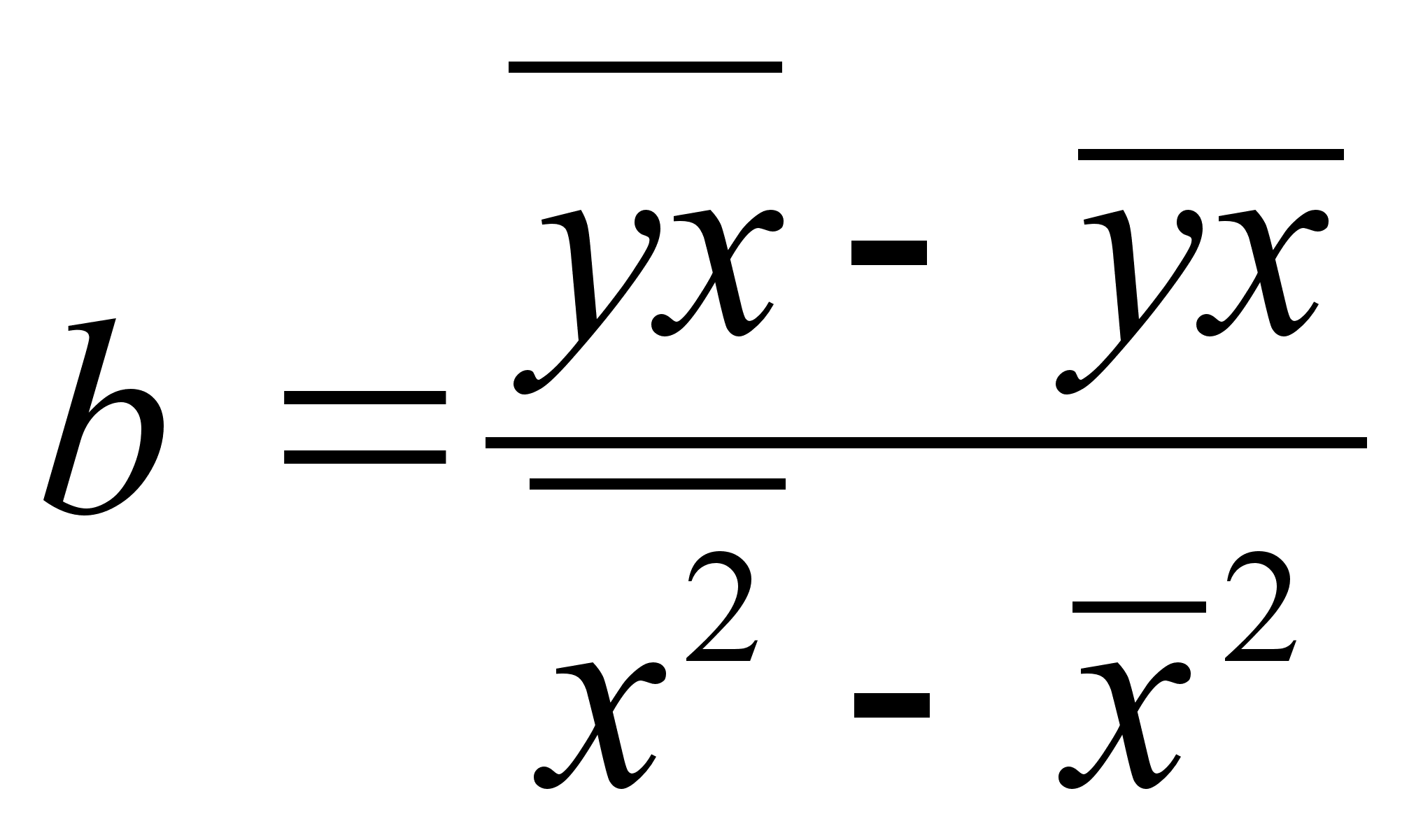 Его величина показывает ср. изменение результата с изменением фактора на 1 ед. Его величина показывает ср. изменение результата с изменением фактора на 1 ед.Ошибка аппроксимации: 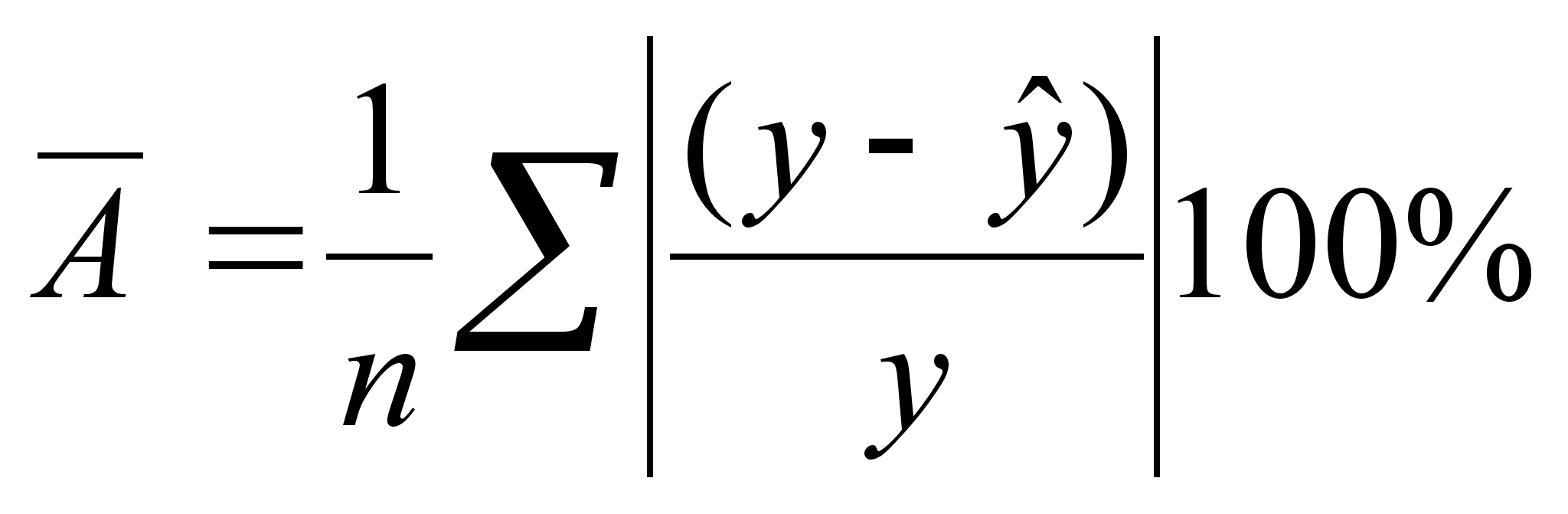 |