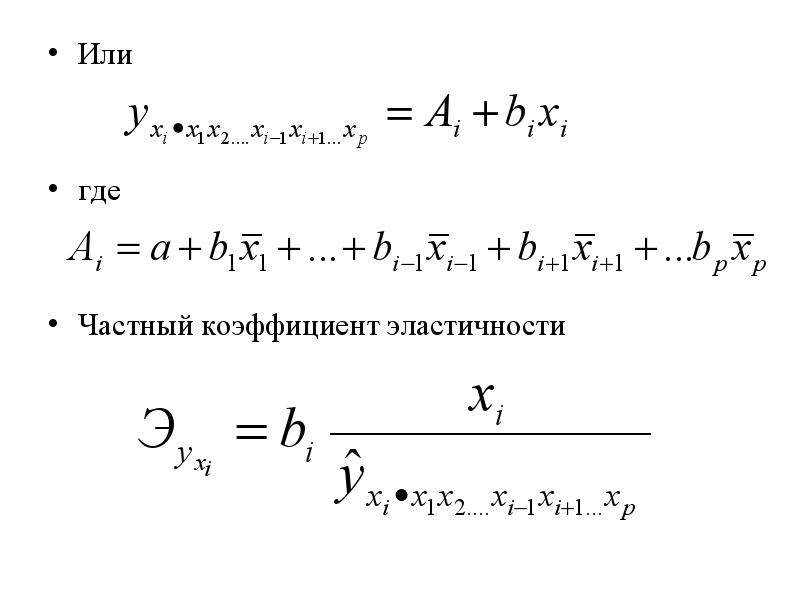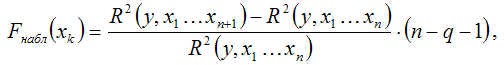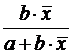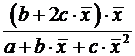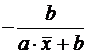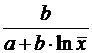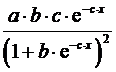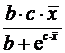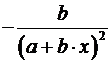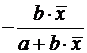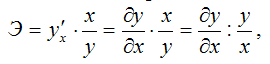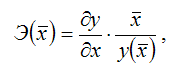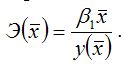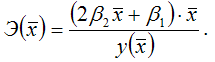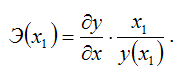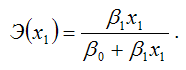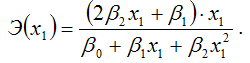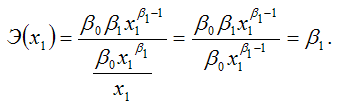|
|
35 Моделирование тенденции временного ряда. 35 Моделирование тенденции временного ряда
21 Множественная корреляция (multiple correlation)
Множественная корреляция (multiple correlation)
М. к. — метод многомерного анализа, широко применяемый в психологии и др. поведенческих науках. М. к. можно рассматривать как расширение двумерной корреляции, а ее коэффициент — как показатель степени связи одной переменной с оптимально взвешенной комбинацией неск. др. переменных. Веса этих переменных определяются методом наименьших квадратов, так чтобы минимизировать остаточную дисперсию.
Коэффициент М. к. принимает значения от 0 до 1 и интерпретируется аналогично коэффициенту двумерной корреляции, если справедливы допущения о прямолинейности и др. характеристиках двумерных интеркорреляций, на основе к-рых вычисляется этот коэффициент.
В психологии квадрат множественной корреляции (R2) или, как его еще наз., коэффициент множественной детерминации, часто используется для оценки доли дисперсии зависимой переменной, приходящейся на совокупность независимых переменных. Родственный метод — множественная регрессия — используется для предсказания зависимой переменной (или критерия) по совокупности независимых переменных (или предикторов).
20

Частные уравнения регрессии Частное уравнение регрессии связывает результативный фактор с фактором xi при фиксировании остальных экзогенных переменных
На основе линейного уравнения множественной регрессии На основе линейного уравнения множественной регрессии могут быть найдены частные уравнения регрессии

Частные уравнения регрессии имеют следующий вид:

Или где Частный коэффициент эластичности
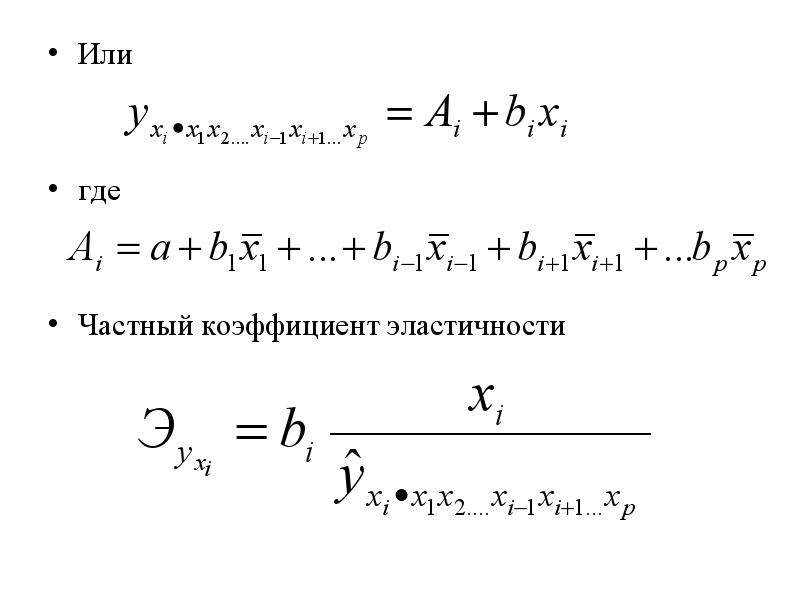
В отличие от парной регрессии частные уравнения регрессии характеризуют изолированное влияние фактора на результат, т.к. другие факторы закреплены на неизменном уровне.

18 1. Основная цель множественнойрегрессии – построить модель с большимчислом факторов, определив при этомвлияние каждого из них в отдельности, атакже совокупное их воздействие намоделируемый показатель.
2. Факторы не должны быть интеркоррелированы и тем более находиться в точной функциональной связи Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям: 1. Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность. спецификации модели: отбор факторов и выбор вида уравнения регрессии.2.
Включаемые во множественную регрессию факторы должны объяснить вариацию независимой переменной Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный показатель и параметры уравнения регрессии оказываются неинтерпретируемыми. Включение в модель факторов с высокой интеркорреляцией (т.е. корреляции между объясняющими переменными), может привести к нежелательным последствиям – система нормальных уравнений может оказаться плохо обусловленной и повлечь за собой неустойчивость и ненадежность оценок коэффициентов регрессии.3.
Если же этого не происходит и данные показатели практически не отличаются друг от друга, то включаемый в анализ фактор не улучшает модель и практически является лишним фактором. и . При дополнительном включении в регрессию m фактора коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться: Если строится модель с набором m факторов, то для нее рассчитывается показатель детерминации , который фиксирует долю объясненной вариации результативного признака за счет рассматриваемых в регрессии факторов. Влияние других, не учтенных в модели факторов, оценивается как с соответствующей остаточной дисперсией .4.
Коэффициенты интеркорреляции (т.е. корреляции между объясняющими переменными) позволяют исключать из модели дублирующие факторы. Считается, что две переменные явно коллинеарны, т.е. находятся между собой в линейной зависимости, если . Если факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии Поэтому отбор факторов осуществляется в две стадии: на первой подбираются факторы исходя из сущности проблемы; на второй – на основе матрицы показателей корреляции определяют статистики для параметров регрессии. Насыщение модели лишними факторами не снижает величину остаточной дисперсии и не увеличивает показатель детерминации и приводит к статистической незначимости параметров регрессии по критерию Стьюдента5.
Пусть, например, при изучении зависимости матрица парных коэффициентов корреляции оказалась следующей:Очевидно, что факторы х1 и х2 дублируют друг друга. В анализ целесообразно включить фактор х2, а не х1. Поэтому в данном случае в уравнение множественной регрессии включаются факторы х2, х3.6.
По величине парных коэффициентов корреляции обнаруживается лишь явная коллинеарность факторов. Наибольшие трудности в использовании аппарата множественной регрессии возникают при наличии мультиколлинеарности факторов, когда более чем два фактора связаны между собой линейной зависимостью, т.е. имеет место совокупное воздействие факторов друг на друга. Наличие мультиколлинеарности факторов может означать, что некоторые факторы будут всегда действовать в унисон. В результате вариация в исходных данных перестает быть полностью независимой и нельзя оценить воздействие каждого фактора в отдельности.7.
Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами. Оценки параметров ненадежны, обнаруживают большие стандартные ошибки и меняются с изменением объема наблюдений (не только по величине, но и по знаку), что делает модель непригодной для анализа и прогнозирования. Затрудняется интерпретация параметров множественной регрессии как характеристик действия факторов в «чистом» виде, ибо факторы коррелированы; параметры линейной регрессии теряют экономический смысл. Включение в модель мультиколлинеарных факторов нежелательно в силу следующих последствий:8.
Существует ряд подходов преодоления сильной межфакторной корреляции. Самый простой путь устранения мультиколлинеарности состоит в исключении из модели одного или нескольких факторов. Другой подход связан с преобразованием факторов, при котором уменьшается корреляция между ними. Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.9.
Рассматриваемое уравнение включает взаимодействие первого порядка (взаимодействие двух факторов). Возможно включение в модель и взаимодействий более высокого порядка, если будет доказана их статистическая значимость по F- критерию Фишера Одним из путей учета внутренней корреляции факторов является переход к совмещенным уравнениям регрессии, т.е. к уравнениям, которые отражают не только влияние факторов, но и их взаимодействие. Так, если , то возможно построение следующего совмещенного уравнения:10.
При отборе факторов также рекомендуется пользоваться следующим правилом: число включаемых факторов обычно в 6–7 раз меньше объема совокупности, по которой строится регрессия. Если это соотношение нарушено, то число степеней свободы остаточной дисперсии очень мало. Это приводит к тому, что параметры уравнения регрессии оказываются статистически незначимыми, а -критерий меньше табличного значения. Шаговый регрессионный анализ – исключение ранее введенного фактора. Метод включения – дополнительное введение фактора. Метод исключения – отсев факторов из полного его набора. Наиболее широкое применение получили следующие методы построения уравнения множественной регрессии: Отбор факторов, включаемых в регрессию, является одним из важнейших этапов практического использования методов регрессии. Подходы к отбору факторов на основе показателей корреляции могут быть разные. Они приводят построение уравнения множественной регрессии соответственно к разным методикам. В зависимости от того, какая методика построения уравнения регрессии принята, меняется алгоритм ее решения на ЭВМ.11.
Классический подход к оцениванию параметров линейной модели множественной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака от расчетных минимальна: (2.2) Рассмотрим линейную модель множественной регрессии (2.1)12.
Находим частные производные первого порядка: Итак. Имеем функцию аргумента: Как известно из курса математического анализа, для того чтобы найти экстремум функции нескольких переменных, надо вычислить частные производные первого порядка по каждому из параметров и приравнять их к нулю.13.
где – стандартизированные переменные: , , для которых среднее значение равно нулю: , а среднее квадратическое отклонение равно единице: ; – стандартизированные коэффициенты регрессии. Метод наименьших квадратов применим и к уравнению множественной регрессии в стандартизированном масштабе:14.
Стандартизованные коэффициенты регрессии показывают, на сколько единиц изменится в среднем результат, если соответствующий фактор изменится на одну единицу при неизменном среднем уровне других факторов. В силу того, что все переменные заданы как центрированные и нормированные, стандартизованные коэффициенты регрессии можно сравнивать между собой. Сравнивая их друг с другом, можно ранжировать факторы по силе их воздействия на результат. В этом основное достоинство стандартизованных коэффициентов регрессии в отличие от коэффициентов «чистой» регрессии, которые несравнимы между собой.15.
Коэффициенты «чистой» регрессии связаны со стандартизованными коэффициентами регрессии следующим образом: где и – коэффициенты парной и межфакторной корреляции. Применяя МНК к уравнению множественной регрессии в стандартизированном масштабе, получим систему нормальных уравнений вида (2.5)16.
т.е. уравнения регрессии, которые связывают результативный признак с соответствующим фактором при закреплении остальных факторов на среднем уровне. В развернутом виде систему (2.8) можно переписать в виде: могут быть найдены частные уравнения регрессии: (2.8) (2.7) На основе линейного уравнения множественной регрессии Рассмотренный смысл стандартизованных коэффициентов регрессии позволяет их использовать при отсеве факторов – из модели исключаются факторы с наименьшим значением .17.
В отличие от парной регрессии частные уравнения регрессии характеризуют изолированное влияние фактора на результат, ибо другие факторы закреплены на неизменном уровне. Эффекты влияния других факторов присоединены в них к свободному члену уравнения множественной регрессии. Это позволяет на основе частных уравнений регрессии определять частные коэффициенты эластичности:18.
которые показывают на сколько процентов в среднем изменится результат, при изменении соответствующего фактора на 1%. Средние показатели эластичности можно сравнивать друг с другом и соответственно ранжировать факторы по силе их воздействия на результат. Наряду с частными коэффициентами эластичности могут быть найдены средние по совокупности показатели эластичности: (2.11) где –коэффициент регрессии для фактора в уравнении множественной регрессии, – частное уравнение регрессии.19.
Для удобства дальнейших вычислений составляем таблицу ( ): Предполагая, что между переменными y , , существует линейная корреляционная зависимость, найдем уравнение регрессии y по и . Рассмотрим пример (для сокращения объема вычислений ограничимся только десятью наблюдениями). Пусть имеются следующие данные (условные) о сменной добыче угля на одного рабочего y (т), мощности пласта (м) и уровне механизации работ (%), характеризующие процесс добычи угля в 10 шахтах.20.
Оно показывает, что при увеличении только мощности пласта (при неизменном ) на 1 м добыча угля на одного рабочего y увеличится в среднем на 0,854 т, а при увеличении только уровня механизации работ (при неизменном ) на 1% – в среднем на 0,367 т. Откуда получаем, что . Т.е. получили следующее уравнение множественной регрессии: Для нахождения параметров уравнения регрессии в данном случае необходимо решить следующую систему нормальных уравнений:21.
Так как стандартизованные коэффициенты регрессии можно сравнивать между собой, то можно сказать, что мощность пласта оказывает большее влияние на сменную добычу угля, чем уровень механизации работ. Т.е. уравнение будет выглядеть следующим образом: при этом стандартизованные коэффициенты регрессии будут Найдем уравнение множественной регрессии в стандартизованном масштабе:22.
Т.е. увеличение только мощности пласта (от своего среднего значения) или только уровня механизации работ на 1% увеличивает в среднем сменную добычу угля на 1,18% или 0,34% соответственно. Таким образом, подтверждается большее влияние на результат y фактора , чем фактора . Вычисляем: Сравнивать влияние факторов на результат можно также при помощи средних коэффициентов эластичности (2.11):23.
17 ножественная регрессия. Проблемы спецификации модели: отбор факторов при построении множественной регрессии;выбор формы уравнения регрессии
Множественная регрессия широко используется в решении проблем спроса, доходности акций, при изучении функции издержек производства, в макроэкономических расчетах и целого ряда других вопросов эконометрики.
В настоящее время множественная регрессия - один из наиболее распространенных методов в эконометрике. Основная цель множественной регрессии - построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый показатель.
Построение уравнения множественной регрессии начинается с решения вопроса о спецификации модели, который в свою очередь включает 2 круга вопросов: отбор факторов и выбор уравнения регрессии. Отбор факторов обычно осуществляется в два этапа: 1) теоретический анализ взаимосвязи результата и круга факторов, которые оказывают на него существенное влияние;
2) количественная оценка взаимосвязи факторов с результатом. При линейной форме связи между признаками данный этап сводится к анализу корреляционной матрицы (матрицы парных линейных коэффициентов корреляции): ry , y ry , x1 ryx2 .... ry , xm rx 1, y rx1, x2 rx2x 2 .... rx 2, xm ...... rxm , y rxm, x1 rxm , x2 .... rxm , xm где ry , xj - линейный парный коэффициент корреляции, измеряющий тесноту связи между признаками y и хj j=1;m , m -число факторов. rxj , xk - линейный парный коэффициент корреляции, измеряющий тесноту связи между признаками хj и хk j,k =1;m. Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям: 1. Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность (например, в модели урожайности качество почвы задается в виде баллов). 2. Каждый фактор должен быть достаточно тесно связан с результатом (т.е. коэффициент парной линейной корреляции между фактором и результатом должен быть существенным).
3. Факторы не должны быть сильно коррелированы друг с другом, тем более находиться в строгой функциональной связи (т.е. они не должны быть интеркоррелированы). Разновидностью интеркоррелированности факторов является мультиколлинеарность - тесная линейная связь между факторами. Мультиколлинеарность может привести к нежелательным последствиям: 1) оценки параметров становятся ненадежными. Они обнаруживают большие стандартные ошибки. С изменением объема наблюдений оценки меняются (не только по величине, но и по знаку), что делает модель непригодной для анализа и прогнозирования.
2) затрудняется интерпретация параметров множественной регрессии как характеристик действия факторов в «чистом» виде, ибо факторы коррелированны; параметры линейной регрессии теряют экономический смысл; 3) становится невозможным определить изолированное влияние факторов на результативный показатель.
Мультиколлинеарность имеет место, если определитель матрицы межфакторной корреляции близок к нулю:
Если же определитель матрицы межфакторной корреляции близок к единице, то мультколлинеарности нет. Существуют различные подходы преодоления сильной межфакторной корреляции. Простейший из них - исключение из модели фактора (или факторов), в наибольшей степени ответственных за мультиколлинеарность при условии, что качество модели при этом пострадает несущественно (а именно, теоретический коэффициент детерминации -R2y(x1...xm) снизится несущественно).
Определение факторов, ответственных за мультиколлинеарность, может быть основано на анализе матрицы межфакторной корреляции. При этом определяют пару признаков-факторов, которые сильнее всего связаны между собой (коэффициент линейной парной корреляции максимален по модулю). Из этой пары в наибольшей степени ответственным за мультиколлинеарность будет тот признак, который теснее связан с другими факторами модели (имеет более высокие по модулю значения коэффициентов парной линейной корреляции).
Еще один способ определения факторов, ответственных за мультиколлинеарность основан на вычислении коэффициентов множественной детерминации (R2xj(x1,...,xj-1,xj+1,...,xm)), показывающего зависимость фактора xj от других факторов модели x1,..., xj-1, x j+1,..., xm. Чем ближе значение коэффициента множественной детерминации к единице, тем больше ответственность за мультиколлинеарность фактора, выступающего в роли зависимой переменной. Сравнивая между собой коэффициенты множественной детерминации для различных факторов можно проранжировать переменные по степени ответственности за мультиколлинеарность. При выборе формы уравнения множественной регрессии предпочтение отдается линейной функции:
yi =a+b1·x1i+ b2·x2i+...+ bm·xmi+ui
в виду четкой интерпретации параметров.
Данное уравнение регрессии называют уравнением регрессии в естественном (натуральном) масштабе. Коэффициент регрессии bj при факторе хj называют условно-чистым коэффициентом регрессии. Он измеряет среднее по совокупности отклонение признака-результата от его средней величины при отклонении признака-фактора хj на единицу, при условии, что все прочие факторы модели не изменяются (зафиксированы на своих средних уровнях).
Если не делать предположения о значениях прочих факторов, входящих в модель, то это означало бы, что каждый из них при изменении х j также изменялся бы (так как факторы связаны между собой), и своими изменениями оказывали бы влияние на признак-результат.
16
Если оцененную модель регрессии предполагается использовать для изучения экономических связей, то устранение мультиколлинеарных факторов является обязательным, потому что их наличие в модели может привести к неправильным знакам коэффициентов регрессии.
При построении прогноза на основе модели регрессии с мультиколлинеарными факторами необходимо оценивать ситуацию по величине ошибки прогноза. Если её величина является удовлетворительной, то модель можно использовать, несмотря на мультиколлинеарность. Если же величина ошибки прогноза большая, то устранение мультиколлинеарных факторов из модели регрессии является одним из методов повышения точности прогноза.
К основным способам устранения мультиколлинеарности в модели множественной регрессии относятся:
1) один из наиболее простых способов устранения мультиколлинеарности состоит в получении дополнительных данных. Однако на практике в некоторых случаях реализация данного метода может быть весьма затруднительна;
2) способ преобразования переменных, например, вместо значений всех переменных, участвующих в модели (и результативной в том числе) можно взять их логарифмы:
lny=β0+β1lnx1+β2lnx2+ε.
Однако данный способ также не способен гарантировать полного устранения мультиколлинеарности факторов;
Если рассмотренные способы не помогли устранить мультиколлинеарность факторов, то переходят к использованию смещённых методов оценки неизвестных параметров модели регрессии, или методов исключения переменных из модели множественной регрессии.
Если ни одну из факторных переменных, включённых в модель множественной регрессии, исключить нельзя, то применяют один из основных смещённых методов оценки коэффициентов модели регрессии – гребневую регрессию или ридж(ridge).
При использовании метода гребневой регрессии ко всем диагональным элементам матрицы (ХТХ) добавляется небольшое число τ: 10-6 ‹ τ ‹ 0.1. Оценивание неизвестных параметров модели множественной регрессии осуществляется по формуле:
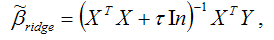
где ln – единичная матрица.
Результатом применения гребневой регрессии является уменьшение стандартных ошибок коэффициентов модели множественной регрессии по причине их стабилизации к определённому числу.
Метод главных компонент является одним из основных методов исключения переменных из модели множественной регрессии.
Данный метод используется для исключения или уменьшения мультиколлинеарности факторных переменных модели регрессии. Суть метода заключается в сокращении числа факторных переменных до наиболее существенно влияющих факторов. Это достигается с помощью линейного преобразования всех факторных переменных xi (i=0,…,n) в новые переменные, называемые главными компонентами, т. е. осуществляется переход от матрицы факторных переменных Х к матрице главных компонент F. При этом выдвигается требование, чтобы выделению первой главной компоненты соответствовал максимум общей дисперсии всех факторных переменных xi (i=0,…,n), второй компоненте – максимум оставшейся дисперсии, после того как влияние первой главной компоненты исключается и т. д.
Метод пошагового включения переменных состоит в выборе из всего возможного набора факторных переменных именно те, которые оказывают существенное влияние на результативную переменную.
Метод пошагового включения осуществляется по следующему алгоритму:
1) из всех факторных переменных в модель регрессии включаются те переменные, которым соответствует наибольший модуль линейного коэффициента парной корреляции с результативной переменной;
2) при добавлении в модель регрессии новых факторных переменных проверяется их значимость с помощью F-критерия Фишера. При том выдвигается основная гипотеза о необоснованности включения факторной переменной xk в модель множественной регрессии. Обратная гипотеза состоит в утверждении о целесообразности включения факторной переменной xk в модель множественной регрессии. Критическое значение F-критерия определяется как Fкрит(a;k1;k2), где а – уровень значимости, k1=1 и k2=n–l – число степеней свободы, n – объём выборочной совокупности, l – число оцениваемых по выборке параметров. Наблюдаемое значение F-критерия рассчитывается по формуле:
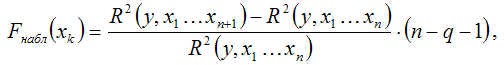
где q – число уже включённых в модель регрессии факторных переменных.
При проверке основной гипотезы возможны следующие ситуации.
Если наблюдаемое значение F-критерия (вычисленное по выборочным данным) больше критического значения F-критерия (определённого по таблице распределения Фишера-Снедекора), т. е. Fнабл›Fкрит, то основная гипотеза о необоснованности включения факторной переменной xk в модель множественной регрессии отвергается. Следовательно, включение данной переменной в модель множественной регрессии является обоснованным.
Если наблюдаемое значение F-критерия (вычисленное по выборочным данным) меньше или равно критического значения F-критерия (определённого по таблице распределения Фишера-Снедекора), т. е. Fнабл≤Fкрит, то основная гипотеза о необоснованности включения факторной переменной xk в модель множественной регрессии принимается. Следовательно, данную факторную переменную можно не включать в модель без ущерба для её качества
3) проверка факторных переменных на значимость осуществляется до тех пор, пока не найдётся хотя бы одна переменная, для которой не выполняется условие Fнабл›Fкрит.
|
|
|
15 10.2. Отбор факторов при построении множественной регрессии
Включение в уравнение множественной регрессии того иного набора факторов связано прежде всего с представлением исследователя о природе взаимосвязи моделируемого показателя с другими экономическими явлениями.
Факторы, включаемые множественную регрессию, должны отвечать следующим требованиям:
Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность (например, в модели урожайности качество почвы задается в виде баллов; в модели стоимости объектов недвижимости учитывается место нахождения недвижимости: они могут быть проранжированы).
Факторы не должны быть интеркоррелированы и тем более находиться в точной функциональной связи. Включение в модель факторов с высокой интеркорреляцией может привести к нежелательным последствиям – система нормальных уравнений может оказаться плохо обусловленной и повлечь за собой неустойчивость и ненадежность оценок коэффициентов регрессии.
Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный показатель и параметры уравнения регрессии оказываются неинтерпретируемыми.
Так, в уравнении у =а +b1x1 + b2х2 +ε предполагается, что факторы x1, их2 независимы друг от друга, т. е. rx1x2 = 0. Тогда можно говорить, что параметрb1 измеряет силу влияния фактора х1, на результату при неизменном значении фактора 2.
Если же rx1x2 = 1, то с изменением фактора x1, фактор х2 не может оставаться неизменным. Отсюда b1 и b2нельзя интерпретировать как показатели раздельного влияния x1, и х2 и на у.
Включаемые во множественную регрессию факторы должны объяснить вариацию независимой переменной. Если строится модель с набором р факторов, то для нее рассчитывается коэффициент детерминации R2 , который фиксирует долю объясненной вариации результативного признака за счет рассматриваемых в регрессии р факторов. Влияние других не учтенных в модели факторов оценивается как 1 - R2 с соответствующей остаточной дисперсиейS2.
При дополнительном включении в регрессию (р +1)-го фактора коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться.
Если же этого не происходит и данные показатели практически мало отличаются друг от друга, то включаемый в анализ факторхр + 1 не улучшает модель и практически является лишним фактором. Насыщение модели лишними факторами не только не снижает величину остаточной дисперсии и не увеличивает показатель детерминации, но и приводит к статистической незначимости параметров регрессии по t-критерию Стьюдента.
Таким образом, хотя теоретически регрессионная модель позволяет учесть любое число факторов, практически в этом нет необходимости.
Как и в парной зависимости, возможны разные виды уравнений множественной регрессии: линейные и нелинейные. Ввиду четкой интерпретации параметров наиболее широко используются линейная и степенная функции. В линейной множественной регрессииу = а + b1x1 +b2х2 + ... + bр• хр параметры при хназываются коэффициентами «чистой» регрессии. Они характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизмененном значении других факторов, закрепленных на среднем уровне.
Отбор факторов, включаемых в регрессию, является одним из важнейших этапов практического использования методов регрессии. Подходы к отбору факторов на основе показателей корреляции могут быть разные. Они приводят построение уравнения множественной регрессии соответственно к разным методикам. В зависимости от того, какая методика построения уравнения регрессии принята, меняется алгоритм ее решения на ЭВМ.
Наиболее широкое применение получили следующие методы построения уравнения множественной регрессии:
метод исключения;
метод включения;
шаговый регрессионный анализ.
Каждый из этих методов по-своему решает проблему отбора факторов, давая в целом близкие результаты – отсев факторов из полного его набора (метод исключения), дополнительное введение фактора (метод включения), исключение ранее введенного фактора (шаговый регрессионный анализ).
При отборе факторов рекомендуется пользоваться следующим правилом: число включаемых факторов обычно в 6—7 раз меньше объема совокупности, по которой строится регрессия. Если это соотношение нарушено, то число степеней свободы остаточной вариации очень мало. Это приводит к тому, что параметры уравнения регрессии оказываются статистически незначимыми, а F-критерий меньше табличного значения.
11 Коэффициент эластичности показывает относительное изменение исследуемого экономического показателя под действием единичного относительного изменения экономического фактора, от которого он зависит при неизменных остальных влияющих на него факторов.
Коэффициент эластичности показывает, на сколько процентов измениться в среднем результат, если фактор изменится на 1%.
Формула для расчета коэффициента эластичности имеет вид: 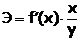
Обычно рассчитывается средний коэффициент эластичности: 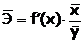 . .
Формулы для расчета средних коэффициентов эластичности для наиболее часто используемых типов уравнений регрессии:
-
Вид функции, y
|
Первая производная, y'
|
Средний коэффициент эластичности, 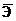
|
1
|
2
|
3
|
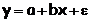
|
b
|
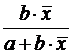
|
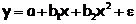
|
b1+2b2x
|
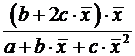
|
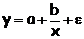
|
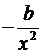
|
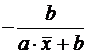
|
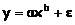
|
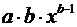
|
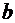
|
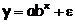
|
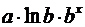
|
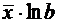
|
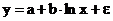
|
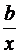
|
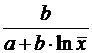
|
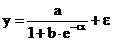
|
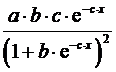
|
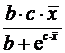
|
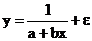
|
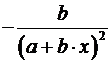
|
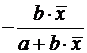
|
Несмотря на широкое применения в эконометрике коэффициентов эластичности, возможны случаи, когда расчет коэффициента эластичности не имеет смысла. Это происходит тогда, когда для рассматриваемых признаков бессмысленно определение изменения в процентах.
10
Коэффициенты эластичности наряду с индексами корреляции и детерминации для нелинейных форм связи применяются для характеристики зависимости между результативной переменной и факторными переменными. С помощью коэффициентов эластичности можно оценить степень зависимости между переменными х и у.
Коэффициент эластичности показывает, на сколько процентов изменится величина результативной переменной у, если величина факторной переменной изменится на 1 %.
В общем случае коэффициент эластичности рассчитывается по формуле:
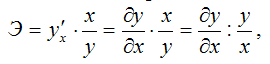
где
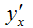
– первая производная результативной переменной у по факторной переменной x.
Коэффициенты эластичности могут быть рассчитаны как средние и точечные коэффициенты.
Средний коэффициент эластичности характеризует, на сколько процентов изменится результативная переменная у относительно своего среднего уровня
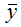
если факторная переменная х изменится на 1 % относительного своего среднего уровня
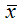
Общая формула для расчёта коэффициента эластичности для среднего значения
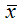
факторной переменной х:
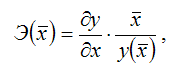
где
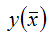
– значение функции у при среднем значении факторной переменной х.
Для каждой из разновидностей нелинейных функций средние коэффициенты эластичности рассчитываются по индивидуальным формулам.
Для линейной функции вида:
yi=β0+β1xi,
средний коэффициент эластичности определяется по формуле:
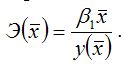
Для полиномиальной функции второго порядка (параболической функции) вида:
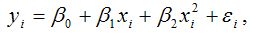
средний коэффициент эластичности определяется по формуле:
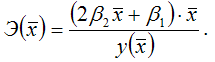
Для показательной функции вида:
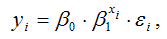
средний коэффициент эластичности определяется по формуле:
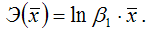
Для степенной функции вида:
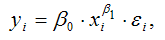
средний коэффициент эластичности определяется по формуле:
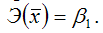
Это единственная нелинейная функция, для которой средний коэффициент эластичности
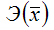
равен коэффициенту регрессии β1.
Точечные коэффициенты эластичности характеризуются тем, что эластичность функции зависит от заданного значения факторной переменной х1.
Точечный коэффициент эластичности характеризует, на сколько процентов изменится результативная переменная у относительно своего значения в точке х1, если факторная переменная изменится на 1 % относительно заданного уровня х1.
Общая формула для расчёта коэффициента эластичности для заданного значения х1факторной переменной х:
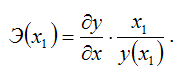
Для каждой из разновидностей нелинейных функций средние коэффициенты эластичности рассчитываются по индивидуальным формулам.
Для линейной функции вида:
yi=β0+β1xi,
точечный коэффициент эластичности определяется по формуле:
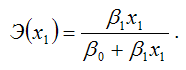
В знаменателе данного показателя стоит значение линейной функции в точке х1.
Для полиномиальной функции второго порядка (параболической функции) вида:
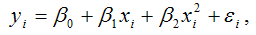
точечный коэффициент эластичности определяется по формуле:
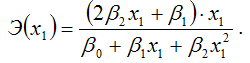
В знаменателе данного показателя стоит значение параболической функции в точке х1.
Для показательной функции вида:
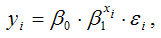
точечный коэффициент эластичности определяется по формуле:
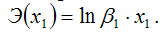
Для степенной функции вида:
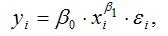
точечный коэффициент эластичности определяется по формуле:
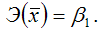
Докажем данное утверждение.
Запишем точечный коэффициент эластичности для степенной функции вида
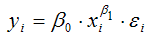
через первую производную результативной переменной по заданной факторной переменной x1:
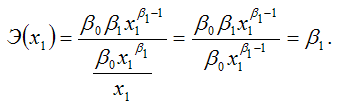
Следовательно, Э(x1) = β1, что и требовалось доказать.
Чаще всего коэффициенты эластичности применяются в анализе производственных функций. Однако их расчёт не всегда имеет смысл, потому что в некоторых случаях интерпретация факторных переменных в процентном отношении невозможна или бессмысленна.
|
|
| |
|
|
 Скачать 1.88 Mb.
Скачать 1.88 Mb.