81. Рождаемость населения, репродуктивное поведение. Показатели рождаемости (методика расчета)

• Название: 81. Рождаемость населения, репродуктивное поведение. Показатели рождаемости (методика расчета)
• Анкор: 81-163.doc
• Дата: 06.03.2018
• Размер: 2.9 Mb.
• Имя файла: 81-163.doc
• Тип: Документы; #16323
• страница: 16 из 16

σ

m_M = ± ---------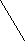



n

2) доверительных границ средних (или относительных) величин;

- границы средних (или относительных) величин, выход за пределы которых вследствие случайных колебаний имеет незначительную вероятность.

Вероятность попадания средней или относительной величины в доверительный интервал называется доверительной вероятностью.

3) достоверности разности средних (или относительных) величин (по критерию t - Стъюдента).

полученные для разных групп населения по полу, возрасту, а также групп больных и здоровых и т.д. Во всех случаях при сопоставлении двух сравниваемых величин возникает необходимость не только определить их разность, но и оценить ее достоверность.

Достоверность разности величин, полученных при выборочных исследованиях, означает, что вывод об их различии может быть перенесен на соответствующие генеральные совокупности.

Достоверность разности выборочной совокупности измеряется доверительным критерием, который рассчитывается по специальным формулам для средних и относительных величин.

Формула оценки достоверности разности сравниваемых средних величин:

M₁ - M₂

t = ------------------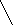



m₁² + m₂²
Для относительных величин:

Р₁ - Р₂

t = ------------------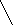




m₁² + m₂²
162. Корреляция.

Раз­личают две формы связи меж явлениями в природе и обществе: функциональную и корреляционную.При корреляционной связи значению каждой средней величины одного признака соответствует множество случайных значений друго­го взаимосвязанного с ним признака.

Например: Вес человека, при прочих равных, зависит в основном от его роста. Однако по­мимо роста на величину веса влияют и другие факторы: питание, сос­тояние здоровья и т.д. Поэтому у лиц одинакового роста относи­тельно редко встречаются одни и те же величины веса, обычно вес варьирует в определенных пределах.

При наличии действительной связи, установленной на основе конкретного анализа, статистика дает возможность измерить силу этой связи и установить степень зави­симости между изучаемыми явлениями.

Коэффициент корреляции одним числом измеряет силу связи между изучаемыми явлениями, а знак дает представление о ее направле­нии.

При положительной (прямой) связи, когда из­менение одного какого-либо явления идет в том же направлении, что и другого коэффициент корреляции может принимать любое значение в пределах от 0 до + 1.

В случае отрицательной (обратной) связи, когда изменение одного из изучаемых явлений сопровождается изменением другого в обратном направлении коэффициент корреляции выражается отрицательным числом и соответственно нахо­дится в пределах от 0 до (-1).

Чем ближе величина коэффициента корреляции к 1, тем соответственно сильнее (теснее) измеряемая им прямая или обратная связь. Коэффициент корреляции, равный 0, говорит о полном отсутствии связи.

Последовательность расчета коэффициента корреляции методом квадратов:1.Расчет средних М_х и М_y для рядов «х» и «y».2.Вычисление отклонений каждой варианты ряда «х» и ряда «y» от их средних М_х и М_y.3.Возведение отклонений d_x и d_y в квадрат.4.Вычисление произведения d_x · d_y5.Определение сумм d_x², d_y² и d_x · d_y.6.Вычисление коэффициента корреляции по формуле:

Σ d_x · d_y

r_xy = ------------------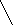




Σ d_x² · d_y²

7.Определение направления и силы связи (см. таблицу 2.14).

8.Расчет ошибки коэффициента корреляции по формуле: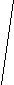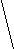



1 – r²_xy

m_r = ± -------------

n - 2
9.Оценка достоверности коэффициента корреляции. t = r_xy / m_r

Коэффициент корреляции достоверен, если он превышает свою ошибку в 3 и более раз.

можно использовать вычисление коэффициента корреляции рангов по методу Спирмена (ρ).

Схема вычисления коэффициента корреляции методом рангов между возрастом студентов медицинского университета и их массой тела

Последовательность расчета коэффициента корреляции методом рангов:

1.Составление рядов парных признаков х и y.

2.Замена каждой величины признака ранговым (порядковым) но­мером - х₁ и y₁.

При обозначении показателей рангами, начинают с меньшего (или с большего) в обоих рядах. Если отдельные показатели ряда встречаются несколько раз (например, 22; 23; 24), ранги проставляются следующим образом: возраст 22 года – встречается дважды, занимая по величине 2 и 3 ранговые места, поэтому порядковые номера в этом случае будут равны полусумме занимаемых этим возрастом мест - (2 + 3) : 2 = 2,5, то есть против каждого показателя возраста 22 года проставляется ранг 2,5. Возраст 23 года встречается 3 раза, занимая 4, 5 и 6 ранговые места. Ранги для возраста 23 года будут равны: (4 + 5 + 6) : 3 = 5, то есть против каждого показателя возраста 23 года проставляется ранг 5 и т.д.

3.Определение разности рангов d = x₁ - y₁.

4.Возведение в квадрат разности рангов - d².

5.Получение суммы квадратов разности рангов Σd².

6.Вычисление коэффициента ранговой корреляции по формуле:

6 · Σd²

ρ_xy = 1 - ---------------

n · (n² – 1)
6 - постоянный коэффициент,

n - число наблюдений.

7.Определение направления и силы связи (см. таблицу )8.Расчет ошибки коэффициента ранговой корреляции m_ρ по фор­муле: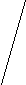

1- ρ²_xy

m_ρ = ± -----------------

n - 2
9.Расчет критерия t и оценка достоверности коэффициента корреляции:

ρ_xy

t = ----------

m_ρ
Метод Спирмена имеет некоторые преимущества перед методом Пирсона.

1. Метод Спирмена можно использовать при открытых значениях вариант (< 20; > 15 и т.д.).

2. Метод Спирмена можно использовать, если нет возможности измерить числовые значения вариант. Например, если нужно установить есть ли связь между ростом и весом у студентов в аудитории, в которой нет измерительных приборов. Можно проранжировать (построить) студентов по росту и весу. Метод Пирсона в этом случае не применим.

163. Прямой метод стандартизации.
Стандартизация - это метод, позволяющий устра­нить влияние качественной или количественной не­однородности сравниваемых групп на величину ин­тенсивных показателей.

(уровни заболеваемости и смертности обычно наибо­лее высоки у детей и лиц старших возрастных групп, а наиболее низки у лиц молодого и среднего возраста. Следовательно, та группа населения, в составе которой относительно больше детей и лиц старших возрастов, может иметь более высокий уровень заболеваемости и смертности, даже если эти показатели в отдельных возрастных группах у нее ниже.)

Устранение возможного влияния различий в составе сравнивае­мых совокупностей по какому-либо признаку (возрасту, полу, про­фессии) на значение интенсивных показателей достигается путем условного уравнивания составов изучае­мых групп по данному признаку. Если имеются данные о составе групп (совокупностей) по по­лу, профессии и другим признакам, а также чис­ленности заболевших или умерших в каждой группе и, следователь­но, можно определить повозрастные коэффициенты смертности и заболеваемости, то для вычисления стандартизованных коэффициентов прибегают к прямому методу стандартизации.

Стандартизованные показатели - гипотетичес­кие величины, они не дают представления об истинном размере яв­ления, а указывают на то, каковы были бы показатели в группах, если бы различие в их составе было исключено. Этапы расчета стандартизованных показателей.

I этап - расчет интенсивных показателей в отдельных группах по признаку различия (возрасту, полу и т.д.) и по совокупности в целом.

II этап - определение стандарта, т.е. одинакового для срав­ниваемых совокупностей численного состава по данному признаку.

III этап - вычисление ожидаемых абсолютных величин в стан­дарте на основе групповых интенсивных показателей, получение итоговых чисел по сравниваемым совокупностям в целом путем суммирования ожидаемых величин.

IY этап - вычисление стандартизованных показателей для сравниваемых совокупностей.

Способы получения стандарта.1.Сумма изучаемых групп.2.Полусумма изучаемых групп.

3.Численный состав одной из групп.4.Численный состав по литературным данным.

В качестве стандарта (например, при элиминировании различий в возрастном составе) можно принять возрастное распределение од­ной из сравниваемых групп, средний возрастной состав сравнивае­мых групп, либо возрастное распределение третьей группы, особен­но такой, в состав которой входят сравниваемые группы. Стандарт следует выбирать каждый раз применительно к конк­ретно изучаемому материалу и в связи с задачами, стоящими перед исследователями.