Методы решений уравнкений с модулем. Лекция 2 по методам решения уравнений, содержащих переменную под. Абсолютная величина и её свойства
 Скачать 1.17 Mb. Скачать 1.17 Mb.
|
Простейшие уравнения и неравенства с модулемК простейшим (не обязательно простым) уравнениям мы будем относить уравнения, решаемые одним из нижеприведенных равносильных переходов:  Пример 131. 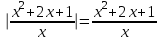 . .Решение 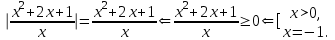 Ответ. 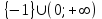 . .Пример 2. 14 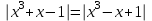 . .Решение 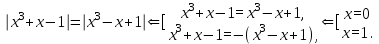 Ответ. 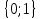 . .Пример 3. 15 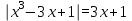 . .Решение 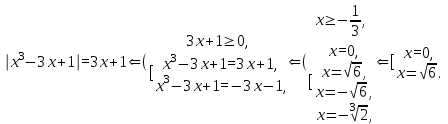 Ответ. 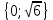 . .Теорема 3. 16Сумма модулей равна алгебраической сумме подмодульных величин тогда и только тогда, когда каждая величина имеет тот знак, с которым она входит в алгебраическую сумму. Пример 4. 17 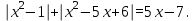 Решение Так как 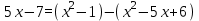 , то мы имеем равенство вида , то мы имеем равенство вида 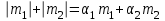 , где , где 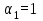 , , 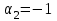 . Поэтому исходное уравнение равносильно системе: . Поэтому исходное уравнение равносильно системе: 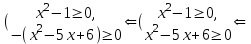  Ответ. 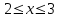 . .Теорема 4. 18Сумма модулей равна модулю алгебраической суммы подмодульных величин тогда и только тогда, когда все величины имеют тот знак, с которым они входят в алгебраическую сумму, либо все величины имеют противоположный знак одновременно. Пример 195. 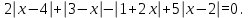 Решение 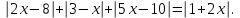 По константам получаем 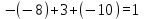 . Действительно, . Действительно, 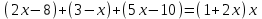 , то есть уравнение имеет вид , то есть уравнение имеет вид 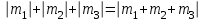 . Следовательно, уравнение равносильно совокупности двух систем: . Следовательно, уравнение равносильно совокупности двух систем: 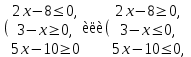 то есть 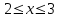 . .Ответ. 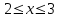 Графическое решение уравнений с модулем Решение уравнений, содержащих знак абсолютной величины часто гораздо удобнее решать не аналитически, а графически (особенно уравнения содержащие параметры). Построение графиков вида 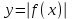 , , 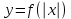 и и 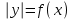 I. Правило построения графика функции 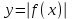 . .1) Строим сначала график функции 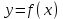 . .2) Там, где график функции 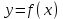 лежит выше оси лежит выше оси 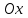 или на ней, оставляем его без изменения; точки графика, которые лежат ниже оси или на ней, оставляем его без изменения; точки графика, которые лежат ниже оси 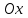 , заменяем симметричными им относительно оси , заменяем симметричными им относительно оси 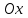 точками. точками.Для примера, на рисунке 1. изображен график функции 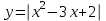 . .  Рис.1 Рис.2. II. Для построения графика функции 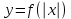 cтроим график функции cтроим график функции 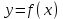 для для 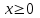 и отображаем симметрично относительно оси и отображаем симметрично относительно оси 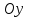 . .Для примера, на рисунке 2. изображен график функции 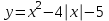 . .III. Для построения графика функции 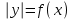 строим график функции строим график функции 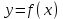 для для 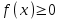 и симметрично отображаем относительно оси и симметрично отображаем относительно оси 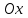 . .Для примера, на рисунке 3. изображен график функции 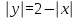 . . рис.3 рис.3Пример 20Построить график функции 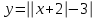 . .Решение.Воспользуемся правилами преобразования графиков. 1. График функции 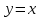 --- биссектриса первого и третьего координатных углов. --- биссектриса первого и третьего координатных углов.2. График функции 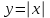 получается из графика функции получается из графика функции 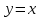 отображением его части, расположенной ниже оси абсцисс (при отображением его части, расположенной ниже оси абсцисс (при  ) симметрично относительно оси абсцисс. ) симметрично относительно оси абсцисс.3. График функции 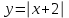 получается из предыдущего сдвигом влево по оси абсцисс на две единицы. получается из предыдущего сдвигом влево по оси абсцисс на две единицы.4. Полученный график сдвигаем по оси ординат на 3 единицы вниз. Получаем график функции 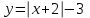 . .5. Часть его, расположенную ниже оси абсцисс, отображаем симметрично относительно этой оси. Итак, получаем график данной функции.  Пример 21На координатной плоскости изобразите все точки, координаты которых являются решениями уравнения: 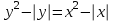 . .Решение.  или или  . . Графики функций, содержащих линейные выражения под знаком абсолютной величины Сформулируем утверждение, позволяющее строить график алгебраической суммы модулей, не раскрывая модули (это особенно удобно, когда модулей много). Теорема 5. 22Алгебраическая сумма модулей 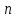 линейных выражений представляет собой кусочно-линейную, график которой состоит из линейных выражений представляет собой кусочно-линейную, график которой состоит из 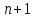 прямолинейного участка. Поэтому график может быть построен по прямолинейного участка. Поэтому график может быть построен по 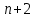 точкам, точкам, 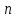 из которых представляют собой корни внутримодульных выражений, ещё одна --- произвольная точка, с абсциссой меньше наименьшего из этих корней, и последняя --- с абсциссой, большей наибольшего из этих корней. из которых представляют собой корни внутримодульных выражений, ещё одна --- произвольная точка, с абсциссой меньше наименьшего из этих корней, и последняя --- с абсциссой, большей наибольшего из этих корней.З  амечание. Аналогично можно строить графики вида амечание. Аналогично можно строить графики вида 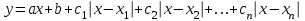 . .Пример построения графиков 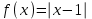 . Вычисляем значения функции в точках 1, 0 и 2, получаем график, состоящий из двух . Вычисляем значения функции в точках 1, 0 и 2, получаем график, состоящий из двух лучей С 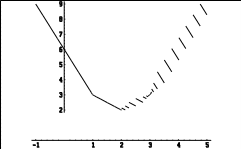 пособы решения уравнений с модулем пособы решения уравнений с модулем |
