Методы решений уравнкений с модулем. Лекция 2 по методам решения уравнений, содержащих переменную под. Абсолютная величина и её свойства
 Скачать 1.17 Mb. Скачать 1.17 Mb.
|
2. Решение уравнений содержащих модули неотрицательных выраженийПример 25Чему равна сумма корней уравнения (корень, если он один) уравнения 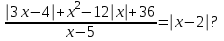 Решение Рассмотрим выражение 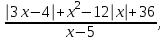 и преобразуем его к виду 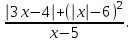 Очевидно, что числитель дроби при любых значениях переменной является положительным числом. Значит дробное выражение положительно, если 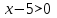 (т.к. (т.к. 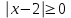 ). Преобразуем полученное выражение, при условии ). Преобразуем полученное выражение, при условии 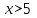 . Получим уравнение, равносильное исходному: . Получим уравнение, равносильное исходному: 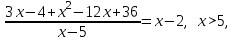 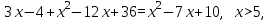 Ответ. 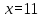 . .Пример 26 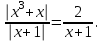 Решение.Поскольку левая часть уравнения неотрицательна, при всех допустимых значениях переменной, на множестве корней уравнения правая его часть тоже должна быть неотрицательной, отсюда условие 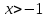 , на этом промежутке знаменатели обеих дробей равны, и остается решить уравнение , на этом промежутке знаменатели обеих дробей равны, и остается решить уравнение 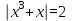 . Решая его графически или используя схему Горнера и свойство коэффициентов, и учитывая ограничение . Решая его графически или используя схему Горнера и свойство коэффициентов, и учитывая ограничение 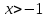 , получаем , получаемОтвет: 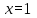 . .3. Решение уравнений с использованием геометрической интерпретацииГеометрический смысл выражения 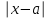 - длина отрезка координатной оси, соединяющего точки с абсциссами - длина отрезка координатной оси, соединяющего точки с абсциссами 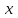 и и 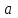 . Перевод алгебраической задачи на геометрический язык часто позволяет избежать громоздких выкладок. . Перевод алгебраической задачи на геометрический язык часто позволяет избежать громоздких выкладок.Пример 27 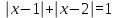 . .Решение Будем рассуждать следующим образом: исходя из геометрической интерпретации модуля, левая часть уравнения представляет собой сумму расстояний от некоторой точки с абсциссой 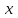 до двух фиксированных точек с абсциссами 1 и 2. Тогда все точки с абсциссами из отрезка до двух фиксированных точек с абсциссами 1 и 2. Тогда все точки с абсциссами из отрезка 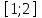 обладают требуемым свойством, а точки, расположенные вне этого отрезка, нет. обладают требуемым свойством, а точки, расположенные вне этого отрезка, нет.Ответ: 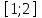 . .Пример 28Решим уравнение 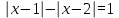 . .Решение Рассуждая аналогично, получим, что разность расстояний до точек с абсциссами 1 и 2 равна единице только для точек, расположенных на координатной оси правее числа 2. Ответ: 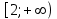 . .Пример 29 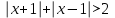 . .Решение Изобразим на координатной прямой точки, сумма расстояний от которых до точек 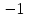 и и 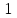 в точности равна в точности равна 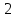 . Это все точки отрезка . Это все точки отрезка 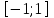 . Для всех чисел вне данного отрезка сумма расстояний будет больше двух. . Для всех чисел вне данного отрезка сумма расстояний будет больше двух.Ответ: 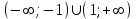 . .Замечание.Обобщением решения вышеприведенных уравнений являются следующие равносильные переходы: 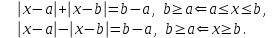 Пример 30 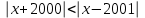 . .Решение Решим неравенство, используя координатную прямую. Данное неравенство выполняется для всех точек c координатой 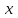 , которые находятся ближе к точке с координатой , которые находятся ближе к точке с координатой  , чем к точке с координатой , чем к точке с координатой 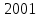 . Так как . Так как 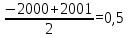 , то искомыми являются все точки, расположенные левее точки с координатой , то искомыми являются все точки, расположенные левее точки с координатой 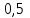 . .Ответ. 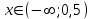 . .Пример 31Решите уравнение 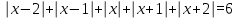 . .Решение Рассмотрим на числовой прямой точку с координатой 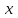 . Сумма . Сумма 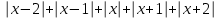 равна сумме расстояний от точки равна сумме расстояний от точки 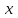 до точек с координатами 2, 1, 0, -1, -2. Заметим, что сумма расстояний от любой точки до точек до точек с координатами 2, 1, 0, -1, -2. Заметим, что сумма расстояний от любой точки до точек 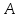 и и 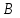 не меньше длины отрезка не меньше длины отрезка 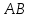 (и равенство достигается тогда и только тогда, когда точка расположена на отрезке (и равенство достигается тогда и только тогда, когда точка расположена на отрезке 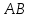 ). Отсюда получаем, что ). Отсюда получаем, что 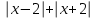 не меньше 4, а не меньше 4, а 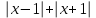 не меньше 2 при любом не меньше 2 при любом 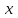 . Поэтому для того, чтобы сумма . Поэтому для того, чтобы сумма 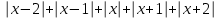 была равна была равна 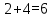 , необходимо, чтобы , необходимо, чтобы 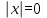 . Итак, . Итак, 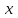 необходимо равен необходимо равен 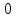 . Легко проверить, что значение . Легко проверить, что значение 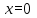 действительно является решением данного уравнения. действительно является решением данного уравнения.Ответ: 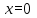 . . |
