|
|
Методы решений уравнкений с модулем. Лекция 2 по методам решения уравнений, содержащих переменную под. Абсолютная величина и её свойства
4. Решение уравнений с использованием тождества 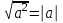
Пример 32
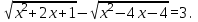
Решение
Дважды применяя тождество 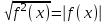 , получим уравнение , получим уравнение
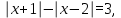
решением которого является интервал 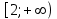 . .
Ответ.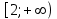 . .
Пример 33
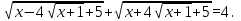
Решение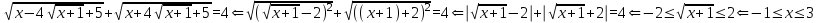 Ответ: Ответ: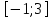 . .
5. Применение теоремы о знаках при решении уравнений
Сформулируем теорему, удобную при решении неравенств, относительно произведений или частных разности модулей:
Теорема 6. 34Знак разности модулей двух выражений совпадает со знаком разности квадратов этих выражений.
Пример 35Решить неравенство

Решение.Воспользуемся теоремой:
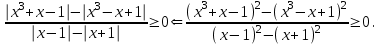
Используя формулу разности квадратов, разложим числитель и знаменатель на множители и решим полученное рациональное неравенство.
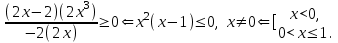
Ответ.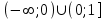
6. Решение уравнений переходом к следствию
Все уравнения с модулями могут быть решены следующим образом: рассмотрим весь набор уравнений, который может получится при раскрытии модулей, но не будем выписывать соответствующие промежутки. Решая каждое из полученных уравнений, получим следствия исходного уравнения. Остается только проверить не приобрели ли мы посторонних корней прямой их подстановкой в исходное уравнение.
Пример 36Решим уравнение
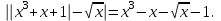
Решение.Последовательно переходя к следствиям, получаем:
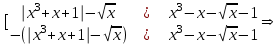
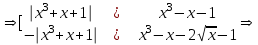
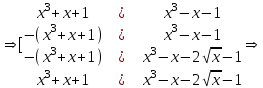
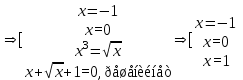
Нетрудно убедится, что найденные числа не являются корнями исходного уравнения.
Ответ.нет решения.
В случае вложенных знаков модуля тоже можно рассмотреть весь набор получающихся при раскрытии модуля уравнений среди решений которых содержатся решения исходного уравнения, а потом отобрать из всех полученных решений подходящие хотя бы с помощью проверки.
Пример 37Решите уравнение
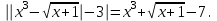
Решение
Все корни исходного уравнения содержатся среди корней двух уравнений
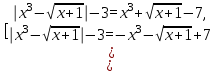
которые можно переписать в виде
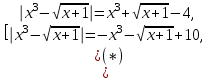
Аналогично, каждое из этих уравнений распадается на два:
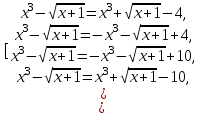
что приводит к четырём уравнениям:
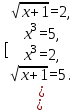
Отсюда получаем 4 решения:  , , 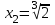 , , 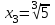 , , 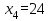 среди которых содержатся корни исходного уравнения. 1-й корень, очевидно, удовлетворяет уравнению. Это проверяется легко. 2-й и 3-й не походят, так как правая часть исходного уравнения при этих значениях отрицательна. 4-й корень тоже является лишним, так как этот корень должен удовлетворять уравнению (*), а при этом значении его правая часть отрицательна. среди которых содержатся корни исходного уравнения. 1-й корень, очевидно, удовлетворяет уравнению. Это проверяется легко. 2-й и 3-й не походят, так как правая часть исходного уравнения при этих значениях отрицательна. 4-й корень тоже является лишним, так как этот корень должен удовлетворять уравнению (*), а при этом значении его правая часть отрицательна.
Ответ.3.
|
|
|
 Скачать 1.17 Mb.
Скачать 1.17 Mb.