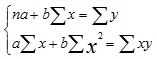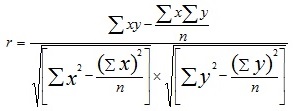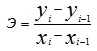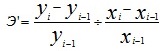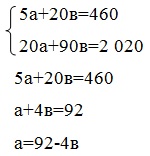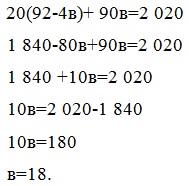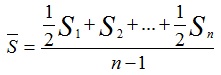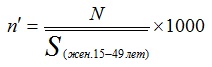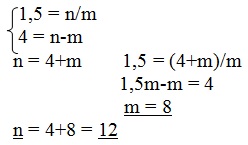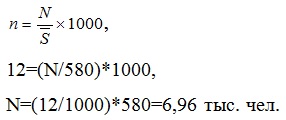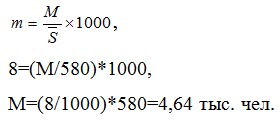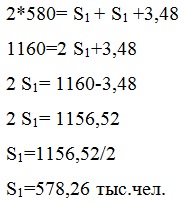контрольные работы по статистике. Абсолютные и относительные величины в статистике. Примеры решения задач
 Скачать 1.69 Mb. Скачать 1.69 Mb.
|
|
Основы корреляционного анализа. Примеры анализа прямолинейной связи при парной корреляции Исследование объективно существующих связей между явлениями - важнейшая задача статистики. В процессе статистического исследования зависимостей выявляются причинно-следственные отношения между явлениями. Причинно-следственные отношения - это такая связь явлений и процессов, когда изменение одного из них - причины ведет к изменению другого - следствия. Признаки явлений и процессов по их значению для изучения взаимосвязи делятся на два класса. Признаки, обуславливающие изменения других, связанных с ними признаков, называют факторными, или просто факторами. Признаки, изменяющиеся под действием факторных признаков, называют результативными. В статистике различают функциональные и стохастические (вероятностные) связи явлений и процессов:
Кроме того, связи между явлениями и их признаками классифицируются по степени тесноты, направлению и аналитическому выражению. По направлению выделяют связь прямую и обратную:
По аналитическому выражению выделяют связи прямолинейные (или просто линейные) и нелинейные:
Теснота связи показывает меру влияния факторного признака на общую вариацию результативного признака.Классификация связи по степени тесноты представлена в таблице 1.
Для выявления наличия связи, ее характера и направления в статистике используются следующие методы: приведения параллельных данных, аналитических группировок, графический, корреляции. Основным методом изучения статистической взаимосвязи является статистическое моделирование связи на основе корреляционного и регрессионного анализа. Корреляция - это статистическая зависимость между случайными величинами, не имеющая строго функционального характера, при которой изменение одной из случайных величин приводит к изменению математического ожидания другой.В статистике принято различать следующие виды корреляции:
Задачей корреляционного анализа является количественное определение тесноты связи между двумя признаками (при парной связи) и между результативным и множеством факторных признаков (при многофакторной связи). Теснота связи количественно выражается величиной коэффициентов корреляции, которые давая количественную характеристику тесноты связи между признаками, позволяют определять «полезность» факторных признаков при построении уравнения множественной регрессии. Корреляция взаимосвязана с регрессией, поскольку первая оценивает силу (тесноту) статистической связи, вторая исследует ее форму. Регрессионный анализ заключается в определении аналитического выражения связи в виде уравнения регрессии. Регрессией называется зависимость среднего значения случайной величины результативного признака от величины факторного, а уравнением регрессии – уравнение описывающее корреляционную зависимость между результативным признаком и одним или несколькими факторными. Формулы корреляционно-регрессионного анализа для прямолинейной связи при парной корреляции представлены в таблице 2.
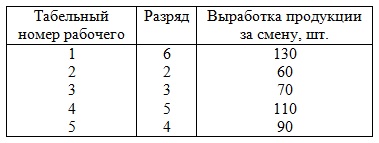
Примеры решения задач по теме «Основы корреляционного анализа» Задача 1 (анализ прямолинейной связи при парной корреляции). Имеются данные о квалификации и месячной выработке пяти рабочих цеха:
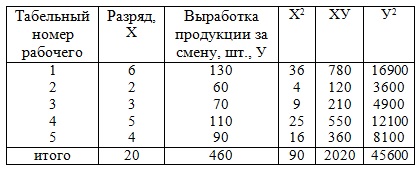
Для изучения связи между квалификацией рабочих и их выработкой определить линейное уравнение связи и коэффициент корреляции. Дать интерпретацию коэффициентам регрессии и корреляции. Решение. Расширим предлагаемую таблицу.
Определим параметры уравнения прямой yx= a +bx. Для этого решим систему уравнений:
Здесь п = 5.
Значит коэффициент регрессии равен 18. Поскольку в - положительное число, то имеется прямая связь между параметрами x и у. а=92-4×18 а=20 Линейное уравнение связи имеет вид ух=20+18х. Для определения тесноты (силы) связи между изучаемыми признаками определим величину коэффициента корреляции по формуле:
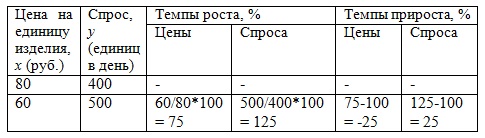
= (2020-20×460/5)/(√10×√3280) ≈ 180/181,11=0,99. Поскольку коэффициент корреляции больше 0,7, то связь в данном ряду сильная. Задача 2. На предприятии цены на изделия снижены с 80 руб. за единицу до 60 руб. После снижения цен продажа возросла с 400 до 500 единиц в день. Определить абсолютную и относительную эластичность. Сделать оценку эластичности с целью возможности (или невозможности) дальнейшего снижения цен. Решение. Рассчитаем показатели, позволяющие провести предварительный анализ эластичности:
Как видим, темпы снижения цены равны по абсолютной величине темпам увеличения спроса. Абсолютную и относительную эластичность найдем по формулам:
= (500-400)/(60-80) =100/(-20) -5 - эластичность абсолютная
= (100:400)/(-20:80) = -1 - эластичность относительная Модуль относительной эластичности равен 1. Это подтверждает тот факт, что темп роста спроса равен темпу снижения цены. В такой ситуации вычислим выручку, получаемую предприятием ранее и после снижения цены: 80*400 = 32 000 руб. в день, 60*500 = 30 000 руб. в день – как видим, выручка снизилась и дальнейшее снижение цен не является целесообразным. Тема №9 Статистический анализ социально-экономического развития общества: примеры решения задач Задача 1. Статистический анализ показателей численности населения Имеются следующие данные за 2012 год:
Определите: коэффициенты рождаемости, смертности, естественного, механического и общего прироста населения; число родившихся; число прибывших на постоянное жительство из других населенных пунктов; специальный коэффициент рождаемости. Решение 1) Зная, как менялась численность населения в 2012 году, найдем среднюю численность населения по формуле:
Sср = (0,5×430+430,2+430,3+430,7+0,5×430,8)/4 = 430,4 тыс. чел. 2) Зная число умерших (М=8170) и коэффициент жизненности (Кжизн.=1,075), определим число родившихся (N) из формулы: Кжизн. = n/m = N/M отсюда N = М*Кжизн. = 8170×1,075 = 8782,75≈8783 чел. 3) Зная число родившихся (N=8783чел.) и среднюю численность населения (Sср = 430,4тыс. чел.), определим коэффициент рождаемости по формуле: n = N/Sср = 8783/430400 = 0,02041 = 20,41‰. 4) Зная число умерших (М=8170чел.) и среднюю численность населения (Sср=430,4тыс. чел.), определим коэффициент смертности: m = M/Sср = 8170/430400 = 0,01898 = 18,98‰. 5) Коэффициент естественного прироста находим по формуле: Кn-m = n-m = 0,02041-0,01898=0,00143 = 1,43‰. 6) Для определения числа прибывших на постоянное жительство из других населенных пунктов найдем абсолютный естественный прирост численности населения: Ае = N-M = 8783-8170 = 613 чел. Далее найдем абсолютный миграционный прирост из равенства: Ам = О - Ае , где О – общий прирост населения (находится как разность между численностью на конец года и начало). Ам=430 800-430 000-613=187чел. Тогда число прибывших (П) найдем из равенства: Ам = П-В, отсюда П=Ам+В=187+570=757 чел. 8) Коэффициент прибытия находим по формуле Кпр = П/Sср = 757:430 400 = 0,00176 = 1,76‰. 9) Коэффициент выбытия находим по формуле Квыб = В/Sср = 570:430400 =0,00132 = 1,32‰. 10) Коэффициент механического прироста находим по формуле Кмиг/мех = Кпр - Квыб =0,00176-0,00132= 0,00044 = 0,44‰. 11) Коэффициент постоянного прироста населения находим по формуле Кобщ = Кn-m + Кмиг = 0,00143-0,00044= 0,00099=0,99‰. 12) Зная, что доля женщин в общей численности населения составляет 58% или 246632 чел., а в возрасте 15-49 лет в общей численности женщин составляет 39% или 97356 чел., найдем специальный коэффициент рождаемости:
= 8783/97356 = 0,09022 = 90,22 ‰. Задача 2. Статистический анализ показателей динамики численности населения По региону известны следующие данные за 2012 г.:
Определите: 1) численность населения на начало и конец 2012 г.; 2) абсолютный естественный и миграционный прирост численности населения, 3) коэффициент миграционного прироста; 4) число родившихся, 5) число умерших; 6) ожидаемую численность населения региона на 01.01.2013 г. Решение Зная коэффициент общего прироста населения (Кобщ=6‰) и коэффициент естественного прироста населения (Кn-m=4‰), найдем коэффициент миграции населения из формулы: Кобщ = Кn-m + Кмиг, отсюда Кмиг = Кобщ - Кn-m = 6 – 4 = 2‰. Поскольку известны коэффициент жизненности населения (Кжизн=1,5‰) и коэффициент естественного прироста населения (Кn-m=4‰), то найдем общий коэффициент рождаемости (n) и общий коэффициент смертности (m), используя формулы: Кжизн = n/m; Кn-m = n-m
Зная общий коэффициент рождаемости, общий коэффициент смертности и среднегодовую численность населения (580 тыс. чел.), найдем число родившихся (N) и число умерших (M) за год.
Найдем абсолютный естественный прирост численности населения: Ае = N-M = 6,96-4,64 = 2,32 тыс.чел. Найдем абсолютный миграционный прирост, воспользовавшись свойством пропорции: Ам = (Ае* Кмиг): Кn-m= 2,32*2/4=1,16 тыс.чел. Тогда общий прирост населения за 2012 год будет равен 2,32+1,16 = 3,48тыс.чел. Численность населения на начало и конец 2012 г. найдем из формулы: Sср = (S1+Sn)/2, где S1 - численность населения на начало 2012 г., Sn=S1+3,48 – численность населения на конец 2012 г.
Sn= S1 +3,48= 578,26+3,48=581,74 тыс.чел. - ожидаемая численность населения региона на 01.01.2013 г. Задача 3. Статистический анализ показателей миграции населения На начало года имеются следующие данные по населенному пункту, тыс. чел.: наличное население - 400; временно проживающие - 4, временно отсутствующие - 2. В течение года произошли следующие изменения, тыс. чел.: родилось всего - 5, в том числе у постоянных жителей - 4,5; умерло всего - 4,3, в том числе у постоян¬ных жителей - 4,2; прибыло на постоянное жительство - 3,5, выехало на постоянное жительство (из числа постоянных жителей) - 1,3. Численность временно проживающих на конец года уменьшилась на 0,3 тыс. чел., а численность временно отсутствующих увеличилась на 0,2 тыс. чел. Определите: численность постоянного населения на начало и конец года; численность наличного населения на конец года; среднегодовую численность постоянного населения; показатели естественного и миграционного движения постоянного населения. Решение 1) Численность постоянного населения на начало года определим по формуле: ПН = НН+ВО-ВП = 400 + 2 - 4 = 398 тыс.чел. За год произошли следующие изменения: НН = 400 + 5 – 4,3 + 3,5 – 1,3 = 402,9 тыс.чел. ВО = 2 + 0,2 = 2,2 тыс.чел. ВП = 4 – 0,3 = 3,7 тыс.чел. (будем считать, что число родившихся – 0,5 тыс.чел. и умерших – 0,1 тыс.чел. а временно проживающих на конец года учтено в указанных изменениях) Тогда численность постоянного населения на конец года будет: ПН=НН+ВО-ВП = 402,9 + 2,2 – 3,7 = 401,4 тыс.чел. 2) Среднегодовую численность постоянного населения определим по формуле: Sср = (S1+Sn)/2 = (398+401,4):2 = 399,7 тыс.чел. 3) Определим показатели естественного движения постоянного населения: - коэффициент рождаемости постоянного населения n = (N/Sср)*1000 = (4,5/399,7)*1000= 11,26‰ ; - коэффициент смертности постоянного населения m = (M/Sср)*1000 = (4,2/399,7)*1000 = 10,5‰ ; - коэффициент естественного прироста постоянного населения Кn-m = n-m = 11,26-10,5= 0,76‰. 4) Определим показатели миграционного движения населения: - коэффициент прибытия населения Кпр = (П/Sср)*1000 = (3,5/399,7)*1000= 8,76‰; - коэффициент выбытия населения Квыб = (В/Sср)*1000= (1,3/399,7)*1000= 3,25‰ ; - коэффициент миграции населения Кмиг=Кпр-Квыб = 8,76-3,25= 5,51‰ . | |||||||||||||||||||||||||||||||||||||||||