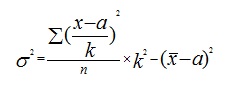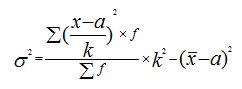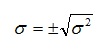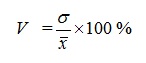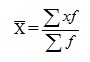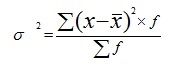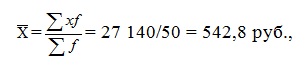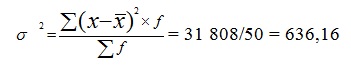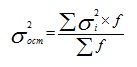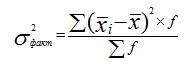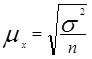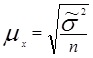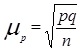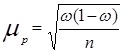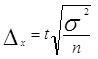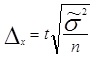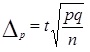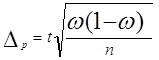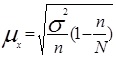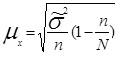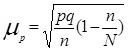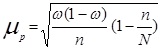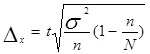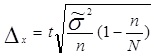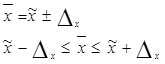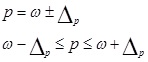контрольные работы по статистике. Абсолютные и относительные величины в статистике. Примеры решения задач
 Скачать 1.69 Mb. Скачать 1.69 Mb.
|
|
Показатели вариации: понятие, виды, формулы для вычислений. Примеры решения задач Часто в статистике при анализе какого-либо явления или процесса необходимо учитывать не только информацию о средних уровнях исследуемых показателей, но и разброс или вариацию значений отдельных единиц, которая является важной характеристикой изучаемой совокупности. В наибольшей степени вариации подвержены курсы акций, объемы спроса и предложения, процентные ставки в разные периоды времени и в разных местах. Основными показателями, характеризующими вариацию, являются размах, дисперсия, среднее квадратическое отклонение и коэффициент вариации. Размах вариации представляет собой разность максимального и минимального значений признака: R = Xmax – Xmin. Недостатком данного показателя является то, что он оценивает только границы варьирования признака и не отражает его колеблемость внутри этих границ. Дисперсия лишена этого недостатка. Она рассчитывается как средний квадрат отклонений значений признака от их средней величины:
Упрощенный способ расчета дисперсии осуществляется с помощью следующих формул (простой и взвешенной):
Примеры применения данных формул представлены в задачах 1 и 2. Широко распространенным на практике показателем является среднее квадратическое отклонение:
Среднее квадратическое отклонение определяется как квадратный корень из дисперсии и имеет ту же размеренность, что и изучаемый признак. Рассмотренные показатели позволяют получить абсолютное значение вариации, т.е. оценивают ее в единицах измерения исследуемого признака. В отличие от них, коэффициент вариации измеряет колеблемость в относительном выражении - относительно среднего уровня, что во многих случаях является предпочтительнее.
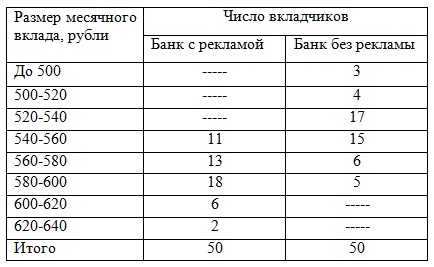
- формула для расчета коэффициента вариации. Примеры решения задач по теме «Показатели вариации в статистике» Задача 1. При изучении влияния рекламы на размер среднемесячного вклада в банках района обследовано 2 банка. Получены следующие результаты:
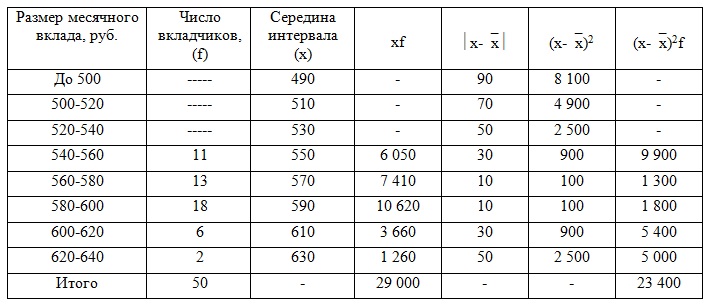
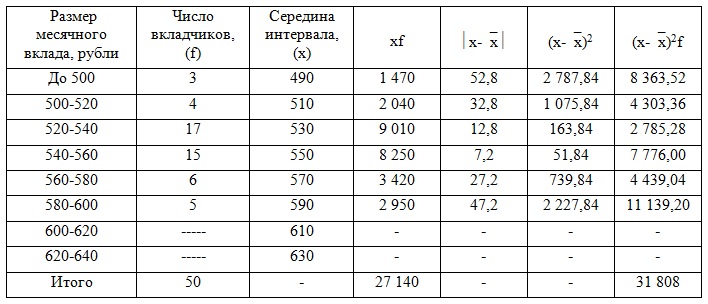
Определить: 1) для каждого банка: а) средний размер вклада за месяц; б) дисперсию вклада; 2) средний размер вклада за месяц для двух банков вместе; 3) Дисперсию вклада для 2-х банков, зависящую от рекламы; 4) Дисперсию вклада для 2-х банков, зависящую от всех факторов, кроме рекламы; 5) Общую дисперсию используя правило сложения; 6) Коэффициент детерминации; 7) Корреляционное отношение. Решение 1) Составим расчетную таблицу для банка с рекламой. Для определения среднего размера вклада за месяц найдем середины интервалов. При этом величина открытого интервала (первого) условно приравнивается к величине интервала, примыкающего к нему (второго).
Средний размер вклада найдем по формуле средней арифметической взвешенной:
= 29 000/50 = 580 руб. Дисперсию вклада найдем по формуле:
= 23 400/50 = 468 Аналогичные действия произведем для банка без рекламы:
2) Найдем средний размер вклада для двух банков вместе. Хср =(580×50+542,8×50)/100 = 561,4 руб. 3) Дисперсию вклада, для двух банков, зависящую от рекламы найдем по формуле: σ2=pq (формула дисперсии альтернативного признака). Здесь р=0,5 – доля факторов, зависящих от рекламы; q=1-0,5, тогда σ2=0,5*0,5=0,25. 4) Поскольку доля остальных факторов равна 0,5, то дисперсия вклада для двух банков, зависящая от всех факторов кроме рекламы тоже 0,25. 5) Определим общую дисперсию, используя правило сложения.
= (468*50+636,16*50)/100=552,08
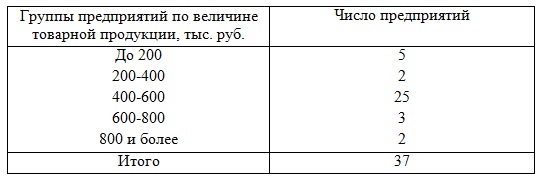
= [(580-561,4)250+(542,8-561,4)250] / 100= 34 596/ 100=345,96 σ2 = σ2факт + σ2ост = 552,08+345,96 = 898,04 6) Коэффициент детерминации η2 = σ2факт / σ2 = 345,96/898,04 = 0,39 = 39% - размер вклада на 39% зависит от рекламы. 7) Эмпирическое корреляционное отношение η = √η2 = √0,39 = 0,62 – связь достаточно тесная. Задача 2. Имеется группировка предприятий по величине товарной продукции:
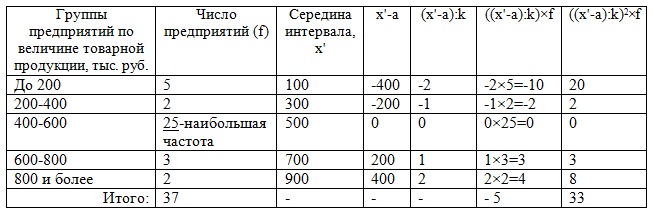
Определить: 1) дисперсию величины товарной продукции; 2) среднее квадратическое отклонение; 3) коэффициент вариации. Решение 1) По условию представлен интервальный ряд распределения. Его необходимо выразить дискретно, то есть найти середину интервала (х'). В группах закрытых интервалов середину найдем по простой средней арифметической. В группах с верхней границей - как разность между этой верхней границей и половиной размера следующего за ним интервала (200-(400-200):2=100). В группах с нижней границей – суммой этой нижней границы и половины размера предыдущего интервала (800+(800-600):2=900). Расчет средней величины товарной продукции делаем по формуле: Хср = k×((Σ((х'-a):k)×f):Σf)+a. Здесь а=500 - размер варианта при наибольшей частоте, k=600-400=200 - размер интервала при наибольшей частоте. Результат поместим в таблицу:
Итак, средняя величина товарной продукции за изучаемый период в целом равна Хср = (-5:37)×200+500=472,97 тыс. руб. 2) Дисперсию найдем по следующей формуле:
σ2 = (33/37)*2002-(472,97-500)2 = 35 675,67-730,62 = 34 945,05 3) среднее квадратическое отклонение: σ = ±√σ2 = ±√34 945,05 ≈ ±186,94 тыс. руб. 4) коэффициент вариации: V = (σ /Хср)*100 = (186,94 / 472,97)*100 = 39,52% тема №4 Выборочное наблюдение: понятие, виды, ошибки выборки, оценка результатов. Примеры решения задач Как известно, в статистике существует два способа наблюдения массовых явлений в зависимости от полноты охвата объекта: сплошное и несплошное. Разновидностью несплошного наблюдения является выборочное наблюдение. Под выборочным наблюдением понимается несплошное наблюдение, при котором статистическому обследованию (наблюдению) подвергаются единицы изучаемой совокупности, отобранные случайным образом. Выборочное наблюдение ставит перед собой задачу – по обследуемой части дать характеристику всей совокупности единиц при условии соблюдения всех правил и принципов проведения статистического наблюдения и научно организованной работы по отбору единиц. Совокупность отобранных для обследования единиц в статистике принято называть выборочной совокупностью, а совокупность единиц, из которых производится отбор, называют генеральной совокупностью. Основные характеристики генеральной и выборочной совокупности представлены в таблице 1.
При проведении выборочного наблюдения возникают систематические и случайные ошибки. Систематические ошибки возникают в силу нарушения правил отбора единиц в выборку. Изменив правила отбора, от таких ошибок можно избавиться. Случайные ошибки возникают в силу несплошного характера обследования. Иначе их называют ошибками репрезентативности (представительности). Случайные ошибки разделяют на средние и предельные ошибки выборки, которые определяются как при расчете признака, так и при расчете доли. Средние и предельные ошибки связаны следующим соотношением: Δ = tμ, где Δ - предельная ошибка выборки, μ - средняя ошибка выборки, t - коэффициент доверия, определяемый в зависимости от уровня вероятности. В таблице 2 приведены некоторые значения t, взятые из теории вероятностей.
Величина средней ошибки выборки рассчитывается дифференцированно в зависимости от способа отбора и процедуры выборки. Основные формулы для расчета ошибок выборки представлены в таблице 3.
Расчет средней и предельной ошибок выборки позволяет определить возможные пределы, в которых будут находиться характеристики генеральной совокупности.
Например, для выборочной средней такие пределы устанавливаются на основе следующих соотношений:
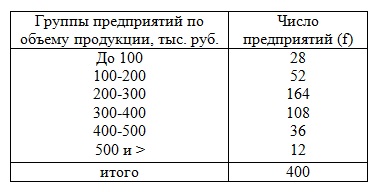
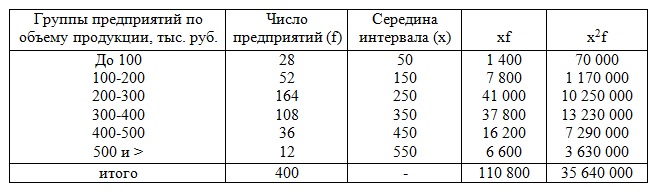
- пределы доли признака в генеральной совокупности р. Примеры решения задач по теме «Выборочное наблюдение в статистике» Задача 1. Имеется информация о выпуске продукции (работ, услуг), полученной на основе 10% выборочного наблюдения по предприятиям области:
Определить: 1) по предприятиям, включенным в выборку: а) средний размер произведенной продукции на одно предприятие; б) дисперсию объема производства; в) долю предприятий с объемом производства продукции более 400 тыс. руб.; 2) в целом по области с вероятностью 0,954 пределы, в которых можно ожидать: а) средний объем производства продукции на одно предприятие; б) долю предприятий с объемом производства продукции более 400 тыс. руб.; 3) общий объем выпуска продукции по области. Решение Для решения задачи расширим предложенную таблицу.
1) По предприятиям, включенным в выборку, средний размер произведенной продукции на одно предприятие
= 110800/400 = 277 тыс. руб. Дисперсию объема производства вычислим упрощенным способом σ2 = 35640000/400 – 2772 = 89100 - 76229 = 12371. Число предприятий, объем производства продукции которых превышает 400 тыс. руб. равно 36+12 = 48, а их доля равна ω = 48:400 = 0,12 = 12%. 2) Из теории вероятности известно, что при вероятности Р=0,954 коэффициент доверия t=2. Предельная ошибка выборки
= 2√12371:400 = 11,12 тыс. руб. Установим границы генеральной средней: 277-11,12 ≤Хср≤ 277+11,12; 265,88 ≤Хср≤ 288,12 Предельная ошибка выборки доли предприятий
=2√0,12*0,88/400 = 0,03 Определим границы генеральной доли: 0,12-0,03≤ р ≤0,12+0,03; 0,09≤ р ≤0,15 3) Поскольку рассматриваемая группа предприятий составляет 10% от общего числа предприятий области, то в целом по области насчитывается 4000 предприятий. Тогда общий объем выпуска продукции по области лежит в пределах 265,88×4000≤Q≤288,12×4000; 1063520 ≤ Q ≤ 1152480 Задача 2. По результатам контрольной проверки налоговыми службами 400 бизнес-структур, у 140 из них в налоговых декларациях не полностью указаны доходы, подлежащие налогообложению. Определите в генеральной совокупности (по всему району) долю бизнес-структур, скрывших часть доходов от уплаты налогов, с вероятностью 0,954. Решение По условию задачи число единиц в выборочной совокупности n=400, число единиц, обладающих рассматриваемым признаком m=140, вероятность Р=0,954. Из теории вероятностей известно, что при вероятности Р=0,954 коэффициент доверия t=2. Долю единиц, обладающих указанным признаком, определим по формуле: p=w+∆p, где w = m/n=140/400=0,35=35%, а предельную ошибку признака ∆p получим из формулы: ∆p= t √w(1-w)/n = 2√0,35×0,65/400 ≈ 0,5 = 5% Тогда р = 35±5%. Ответ: Доля бизнес-структур, скрывших часть доходов от уплаты налогов с вероятностью 0,954 равна 35±5%. тема №5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||