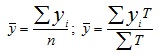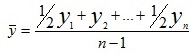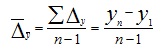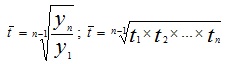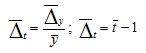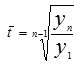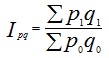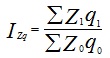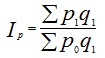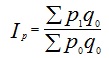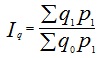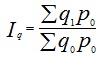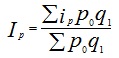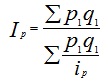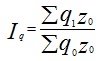контрольные работы по статистике. Абсолютные и относительные величины в статистике. Примеры решения задач
 Скачать 1.69 Mb. Скачать 1.69 Mb.
|
|
Ряды динамики: понятие и классификация. Показатели уровней ряда динамики. Примеры решения задач Процесс развития, движения социально-экономических явлений во времени в статистике принято называть динамикой. Для отображения динамики строят ряды динамики (хронологические, временные), которые представляют собой ряды изменяющихся во времени значений статистического показателя, расположенных в хронологическом порядке. Составными элементами ряда динамики являются показатели уровней ряда и показатели времени (годы, кварталы, месяцы, сутки) или моменты (даты) времени. Уровни ряда обычно обозначаются через «y», моменты или периоды времени, к которым относятся - через «t». Существуют различные виды рядов динамики, которые классифицируют по следующим признакам:
Показатели изменения уровней ряда динамики Анализ скорости и интенсивности развития явления во времени осуществляется с помощью статистических показателей, возникающих в результате сравнения уровней между собой. К таким показателям относятся: абсолютный прирост, темп роста и прироста, абсолютное значение одного процента прироста. При этом принято сравниваемый уровень называтьотчетным, а уровень, с которым происходит сравнение - базисным. Абсолютный прирост (Δу) характеризует размер увеличения (или уменьшения) уровня ряда за определенный промежуток времени. Он равен разности двух сравниваемых уровней и выражает абсолютную скорость роста: Δy = уi-yi-k (i=1,2,3,...,n). Если k=1, то уровень yi-1 является предыдущим для данного уровня, а абсолютные приросты изменения уровня будут цепными. Если же k постоянны для данного ряда, то абсолютные приросты будут базисными. Показатель интенсивности изменения уровня ряда - в зависимости от того, выражается ли он в виде коэффициента или в процентах, принято называть коэффициентом роста (темпом роста). Темп роста (t) показывает во сколько раз данный уровень ряда больше базисного уровня (если этот коэффициент больше единицы) или какую часть базисного уровня составляет уровень текущего периода за некоторый промежуток времени (если он меньше единицы): t = yi / yi-1или t = yi / y1 Темпа прироста (Δt), характеризует относительную скорость изменения уровня ряда в единицу времени. Темп прироста показывает, на какую долю (или процент) уровень данного периода или момента времени больше (или меньше) базисного уровня. Находят темп прироста как отношение абсолютного прироста к уровню ряда, принятого за базу: Δt = Δy / yi-1 или Δt = Δy / y1 или Δt = t-1 (Δt = t-100%). Если темп роста всегда положительное число, то темп прироста может быть положительным, отрицательным и равным нулю. В статистической практике часто вместо расчета и анализа темпов роста и прироста рассматривают абсолютное значение одного процента прироста (А). Оно представляет собой одну сотую часть базисного уровня и в то же время - отношение абсолютного прироста к соответствующему темпу прироста: А= Δy /( Δt*100) = yi-1/100 Средний уровень ряда динамики рассчитывается по средней хронологической. Средней хронологической называется средняя, исчисленная из значений, изменяющихся во времени. Такие средние обобщают хронологическую вариацию. В хронологической средней отражается совокупность тех условий, в которых развивалось изучаемое явление в данном промежутке времени. Формулы для вычисления средних показателей ряда динамики представлены в таблице.
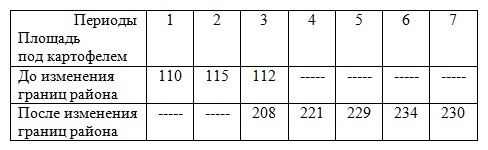
Примеры решения задач по теме «Ряды динамики в статистике» Задача 1. Данные о площадях под картофелем до и после изменения границ района, тысяч гектаров:
Сомкнуть ряд, выразив площадь под картофелем в условиях изменения границ района. Решение
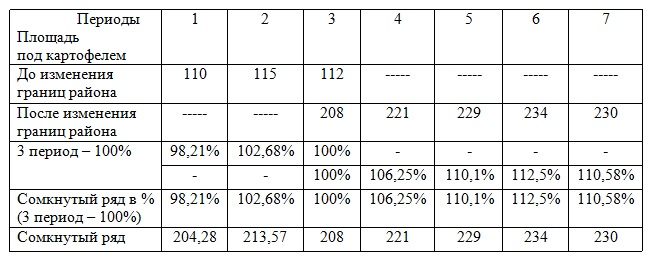
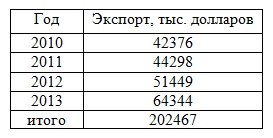
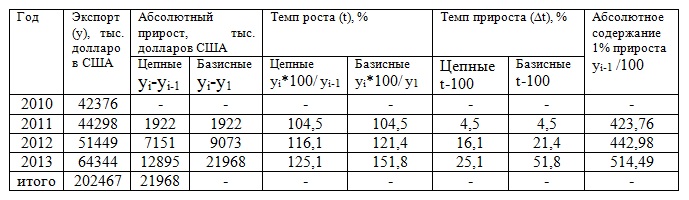
Примем за базу сравнения третий период – период, за который есть данные как в прежних, так и в старых границах района. Затем эти два ряда с одинаковой базой смыкаем в один. Задача 2. Имеется информация об экспорте продукции из региона за ряд лет:
Определить: 1) цепные и базисные: а) абсолютные приросты; б) темпы роста; в) темпы прироста; 2)абсолютное содержание одного процента прироста; 3) средние показатели: а) средний уровень ряда; б) среднегодовой абсолютный прирост; в) среднегодовой темп роста; г) среднегодовой темп прироста. Решение Напомним, что: - если каждый текущий уровень сравнивать с предыдущим, то мы получим цепные показатели; - если каждый текущий уровень сравнивать с первоначальным, то получим базисные показатели. Для решения расширим предложенную таблицу.
Средний уровень ряда определим по средней арифметической простой: Уср=202467:4=50616,75 тыс. долларов США. Среднегодовой абсолютный прирост определим по формуле:
= (64344-42376) / (4-1) = 7322,67 тыс. долларов США. Среднегодовой темп роста определим по формуле:
= 3√(64344:42376) = 1,15=115% Среднегодовой темп прироста определим по формуле:
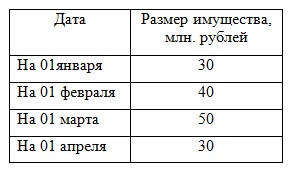
=1,15-1=0,15=15%. Задача 3. По следующей информации определить средний размер имущества предприятия за квартал:
Решение Средний размер имущества предприятия за квартал определим по формуле:
= (30/2 +40 +50 +30/2) / (4-1) = 40 млн. руб. тема №6 Экономические индексы в статистике: понятие, виды, формулы. Примеры решения задач Как известно, «индекс» в переводе с латинского означает «указатель» или «показатель». В статистике индексом называют показатель относительного изменения данного уровня исследуемого явления по сравнению с другим его уровнем, принятым за базу сравнения. В качестве такой базы может быть использован или уровень за какой-либо прошлый период времени (динамический индекс), или уровень того же явления по другой территории (территориальный индекс). В статистической практике индексы являются незаменимым инструментом исследования в тех случаях, когда необходимо сравнить во времени или пространстве две совокупности, элементы которых непосредственно суммировать нельзя. В целом, индексный метод направлен на решение следующих задач:
Простейшим показателем, используемым в индексном анализе, является индивидуальный индекс (i), который характеризует изменение во времени экономических величин, относящихся к одному объекту:
В тех случаях, когда исследуются не единичные объекты, а состоящие из нескольких элементов совокупности, используютсясводные (общие) индексы (I). Исходной формой сводного индекса является агрегатная форма. Формулы для вычисления общих индексов представлены в таблице.
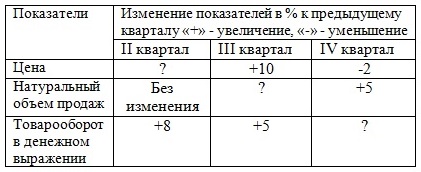
Примеры решения задач по теме «Экономические индексы в статистике» Задача 1. По нижеприведенным данным ответить на вопросы, поставленные в таблице, т.е. определить недостающие показатели.
Решение 1) ІІ квартал: Ip= ?; Iq= 1; Ipq =1,08 Ip = Ipq/Iq = 1,08:1 = 1,08 (в таблицу поместим +8). 2) ІІІ квартал: Ip = 1,1; Iq = ?; Ipq =1,05 Iq = Ipq/Ip = 1,05:1,1 = 0,95 (в таблицу поместим -5). 3) ІV квартал: Ip =0,98; Iq = 1,05; Ipq =? Ipq = Ip×Iq = 0,98×1,05 = 1,029 ≈ 1,03 (в таблицу поместим +3). Итак, заполним таблицу:
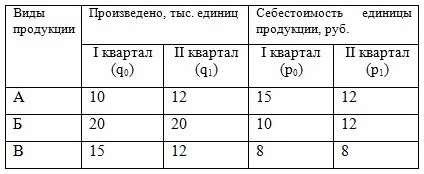
Задача 2. Имеется информация о выпуске продукции на предприятии, ее себестоимости за 2 квартала.
Определить: 1) индивидуальные индексы количества и себестоимости; 2) общие индексы затрат на производство, натурального выпуска и себестоимости; 3) абсолютное изменение затрат на выпуск продукции в целом и по факторам: а) за счет изменения себестоимости; б) за счет изменения натурального выпуска. Сделать выводы. Решение 1) Найдем индивидуальные индексы количества: для продукции А: iq = q1/q0 = 12/10=1,2; для продукции Б: iq = q1/q0 = 20/20=1; для продукции В: iq = q1/q0 = 12/15=0,8 Найдем индивидуальные индексы себестоимости: для продукции А: ip = p1/p0 = 12/15=0,8; для продукции Б: ip = p1/p0 = 12/10=1,2; для продукции В: ip = p1/p0 = 8/8=1 2) общие индексы затрат на производство, натурального выпуска и себестоимости найдем по формулам:
= (12*12+12*20+8*12)/(15*10+10*20+8*15) = 480/470 = 1,021=102,1%
= (12*15+20*10+12*8)/470 = 476/470 = 1,013 = 101,3%
= 480/476 = 1,008=100,8% 3) абсолютное изменение затрат на выпуск продукции в целом:
= 480-470=10 тыс.руб. По факторам: а) за счет изменения себестоимости:
= 480-476=4 тыс.руб. б) за счет изменения натурального выпуска
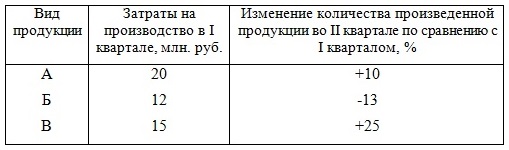
= 476-470 = 6 тыс.руб. Вывод: Товарный выпуск во втором квартале увеличился по сравнению с первым на 102,1-100=2,1%. В абсолютном выражении это соответствует 10 тыс. руб. Этот рост произошел как за счет увеличения объема выпуска (на 101,3-100=1,3% или 6 тыс. руб.), так и за счет себестоимости (100,8-100=0,8% или 4 тыс. руб.). Задача 3. Имеется информация о затратах на производство и индексах количества:
Определить: 1)индивидуальные индексы физического объема производства; 2) общий индекс физического объема производства; 3) общий индекс себестоимости, если известно, что общие затраты на производство выросли на 25%. Сделать выводы. Решение 1) Найдем индивидуальные индексы количества: для продукции А: iq = q1/q0 = (100+10)/100 = 110/100=1,1; для продукции Б: iq = q1/q0 = (100-13)/100 = 87/100=0,87; для продукции В: iq = q1/q0 = (100+25)/100 = 125/100=1,25 2) Поскольку известны затраты на производство в І квартале по каждому виду продукции (z0q0), где z0 - себестоимость продукции, q0- количество произведенной продукции, то найдем: для продукции А: z0q1= z0q0*iq = 20*1,1 = 22; для продукции Б: z0q1= z0q0*iq = 12*0,87 = 10,44; для продукции В: z0q1= z0q0*iq = 15*1,25 = 18,75 Далее найдем общий индекс объема производства:
= (22+10,44+18,75)/(20+12+15)=51,19/47=1,089=108,9% 3) Поскольку общие затраты на производство выросли на 25%, то общий индекс затрат Izq = 1,25. Найдем общий индекс себестоимости: Iz = Izq:Iq = 1,25:1,089 = 1,148 =114,8% Вывод: Увеличение общих затрат на производство во втором квартале на 25% произошло как за счет увеличения объема выпуска на 108,9-100=8,9%, так и за счет увеличения себестоимости на 114,8-100= 14,8%. Тема №7 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||