кулакова 1. Активизация учебнопознавательной деятельности младших школьников. Познавательная деятельность
 Скачать 1.01 Mb. Скачать 1.01 Mb.
|
|
82. Особенности реализации принципов обучения в начальной школе. Существует небольшое число конкретных базовых ЗУНов, которыми должны обладать все выпускники начальной школы. Они должны, в частности, уметь читать, писать и считать. Существуют и общие, называемые иногда общеучебными, умения. К ним относятся умения собирать факты, их сопоставлять, организовывать, выражать свои мысли на бумаге и устно, логически рассуждать, открывать что-то новое, принимать решения и делать выбор. Эти умения можно было бы назвать даже не общеучебными, а общеинтеллектуальными, поскольку они нужны не только в учебной, но и в интеллектуальной деятельности человека вообще. Поскольку такого сорта деятельность становится все более существенной на большинстве рабочих мест, в большинстве профессий, то речь идет вообще о жизненных умениях. (Сейчас стало модным, следуя за некоторыми западными источниками, говорить о компетенциях, или о компетентностях, под которыми понимается умение применять знания и навыки в определенной области в различных реальных практических ситуациях). Есть и еще умения - сопереживать другому человеку, действовать сообща, чувствовать прекрасное, давать моральную оценку своим желаниям и поступкам и следовать нормам, принципам и правилам. Для формирования этих умений (и самых конкретных, базовых, и самых обобщенных и возвышенных), есть много путей. Выбор пути формирования умений определяет школу. На результат влияют как условия, целенаправленно создаваемые учителем, так и случайные обстоятельства (проболел, совпал интерес к увиденному по телевизору с проходимой в школе темой) и ситуации (нелюбимый учитель, в школе нет химреактивов), а также исходными способностями и типом личности ученика. Одним из основных направлений развития современного образования, в частности, должна быть большая степень его индивидуализации, когда мы начнем меньше требовать одного и того же ото всех, но достигать больше своего для каждого и намного большего - для всех вместе. При этом даже для конкретных ЗУНов, которые должен получить каждый (таких как умение складывать числа), будут выбираться индивидуальные пути их усвоения. Обобщенные ЗУНы будут формироваться и на этих разных путях для общих конкретных ЗУНов и на разном материале для разных учащихся. Поощряться и оцениваться будут индивидуальные достижения во всем их разнообразии. Во всем постигаемом индивидуально мы будем добавлять ученику наше признание и формальные баллы за то, что он сделал, а не вычитать за то, что он не сумел. Говоря об образовательной среде и о материальных и информационных средствах, используемых в образовательном процессе, мы часто сосредотачиваемся на том, в какой степени среда соответствует задаче освоения данной системы ЗУНов - конкретного предметного содержания. Мы далеки от того, чтобы преуменьшать роль ЗУНов и роль образовательной среды в их формировании, однако хотели бы остановиться на другом. С течением времени и в образовании и в человеческой цивилизации в целом становится все более ясно, что важнейшим результатом образования являются некоторые общие модели деятельности человека, в том числе, интеллектуальной деятельности, хотя и не только. Речь идет о планировании человеком своей работы и корректировке планов, о способности к контролю результатов работы, ее хода и своего поведения, о кооперации и разделении труда, о стратегиях индивидуального и общего выигрыша, об анализе своего опыта и поиске закономерностей, об умении делать произвольный выбор, строить модели социальных ситуаций и примерять на себя роли, умении спорить, отстаивать свою точку зрения, понимать и принимать точку зрения оппонента и т.д. Замечательно, что многие из умений, которые упомянуты выше, важность которых в общем-то никогда не отрицалась, легко достигаются в тех или иных детских играх и весьма проблематично, с трудом в ситуации урока. Более того, начиная обсуждать это и с практическими российскими учителями, и с профессионалами науки-педагогики наталкиваешься на то, что указанные умения действительно трудно совмещаются с общепринятым содержанием образования¦. В лучшем случае тебе скажут, что все относится к воспитанию и, конечно, воспитание необыкновенно важно, но вот собеседник занимается другим. Не пытаясь провести грань между воспитанием и обучением в образовательном процессе, мы все же попытаемся оспорить сформулированную пессимистическую точку зрения. Мы постараемся обосновать надежду на то, что эффективное достижение стандартных ЗУНов может осуществляться в ходе образовательного процесса, в котором будут широко использоваться модели деятельности (в том числе - игровые), явно и недвусмысленно соотносящиеся с интересующими нас умениями. При этом достаточно существенной оказывается образовательная среда, в которой учебный процесс осуществляется ее субъектами - учеником и учителем.
Изучение прямой линии развивает один из основных компонентов пространственных представлений — понятие о линейной протяженности. Познание линейной протяженности формируется как на уроках математики, так и на уроках рисования, физкультуры, труда, начиная с первых шагов обучения. Параллельно с этим измерительные операции уточняют их знания о протяженности, устанавливают связь между пространственными и количественными представлениями. Постепенно эти ассоциации крепнут, уточняются и развиваются представления о протяженности, сближаются результаты, полученные измерением инструментом и на глаз. В программе для I класса геометрический материал не выделяется особой темой, но имеется указание на развитие пространственных представлений в процессе измерения. Уже на первых уроках можно познакомить учеников I класса с сантиметром и связать изучение чисел и процесс счета с построением отрезков и числовой осью Образ прямой линии можно иллюстрировать при помощи натянутой нити или резинового шнура, ребер геометрических тел, следа на листе бумаги после перегибания его, следа движущейся точки. Ученики могут находить прямые линии на многих предметах, находящихся вокруг них в классе и вне класса, указывают случаи из практики, когда нужно прокладывать прямые линии (при постройке домов, сараев, заборов, дорог, при посадке деревьев и т. д.) 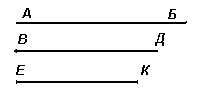 рис. 1 У школьников формируется понятие о прямой линии (неограниченной), о луче, ограниченном начальной точкой, и об отрезке, ограниченном с двух сторон (рис. 1) рис. 2 Для уточнения этих понятий служат разнообразные упражнения. Например, на рисунке 2 дети должны найти прямую, луч, отрезок (прямая АБ, лучи ВА, ВБ, ГБ, ГА, отрезок ВГ). 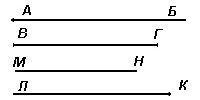 рис. 3 Задание к рисунку 3 состоит в том, что ученики должны выполнить в своих тетрадях аналогичные чертежи и подписать под ними соответственно прямая, луч, отрезок. Интересные упражнения, развивающие детей, можно провести, рассматривая отрезки на прямой (рис. 4). Учащиеся обычно видят только рядом расположенные отрезки. Между тем здесь можно найти отрезки АВ, АГ, БГ и др. Измерением дети убеждаются, что АБ + БВ = АВ и т. д. рис. 4 Построением ряда прямых, проходящих через одну точку, дети убеждаются в том, что таких прямых можно провести «много» (сколько угодно). После этого нетрудно подвести их к аксиоме о прямой, проходящей через 2 точки. Детям дают задания, которые показывают, что через 3,4 точки обычно нельзя провести одну прямую. Понятие о горизонтальном и вертикальном направлении можно показать на сосуде с водой, в который погружена висячая на нитке гиря. Наряду с построением пересекающихся линий, проходящих через одну точку, возможно задание на построение линий, которые надо продолжить до пересечения (рис. 5). 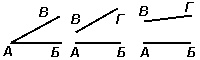 рис. 5 После этого можно дать понятие о непересекающихся линиях(параллельных). Для этой цели сначала используется построение прямых линий на клетчатой бумаге так, чтобы расстояния любой точки одной прямой до другой линии были равны, а потом и на нелинованной бумаге. Построение отрезков следует связать с приобретением навыков обращения с чертежными принадлежностями (линейка, угольник, циркуль). Чертеж — это язык техники. Надо шире использовать чертежи в занятиях с детьми. Практические работы с отрезками сближают арифметику с геометрией. Над отрезками выполняются все арифметические действия, при этом задания проверяются при помощи измерения и вычисления. Изучение прямой линии сопровождается упражнениями в развитии глазомера с постепенным усложнением их от класса к классу. Сначала ученики определяют на глаз длину отрезков, начерченных на доске, длину различных предметов, чертят на глаз отрезки заданной длины. Для того чтобы не было беспочвенного гадания, надо при определении расстояний на глаз ориентироваться на длину начерченных на доске или прикрепленных к ней цветных полосок в 1 метр, 1 дециметр, 1 сантиметр. Упражнения по развитию глазомера можно варьировать различными способами. Расстояния, определенные на глаз, проверяются измерением, устанавливается величина допущенной ошибки. Тем самым закладываются первичные понятия о приближенных величинах, о погрешности.
Понятие "педагогическая технология" может рассматриваться в трех аспектах:
Педагогические технологии – совокупность методов, средств, приемов, используемых в общенииии для достижения положительного результата обучения. Педагогическая технология – поиск ответа на вопрос «как учить всех всему результативно». Понятие «пед. технология» возникло в сер. 20 в. Причины, по которых активизировался процесс поиска пед. технологий: обучение в совр. усл-х носит массовый хар-р (возраст один, а спос-ти разные); требования к кач-ву обучения растут, уровень обучения для всех учеников повышается, а диапазон индив. отличий детей огромен, таким образом, условия в школах – усредненные. Уровни пед. технологий: 1) общепедагогический уровень (создается общепед. технология, кот. дает общ. представление о целостном процессе в определенном регионе на опред. этапе); 2) частно-методический=предметный (пед. технология употребляется в знач-и «методика» – совок-ть средств, методов по реализации опред. содержания в рамках одного предмета); 3)локальный=модульный (решение частных дидактических задач). Структура педагогической технологии: 1) концептуальная основа (осн. теоретич. идея. Напр., раздельное обучение мал. и дев.); 2) содержательная часть обучения (цели обучения – общие и конкретные); 3) процессуальная часть (организация уч. процесса, методы и формы уч. деят-ти шк-ков). Критерии пед. технологий: 1) концептуальность; 2) системность; 3) управляемость; 4) эффективность; 5) воспроизводимость. Пед. технологии: 1) технология трансформирования ЗУН (традиционная): • передача информации от учителя к ученику, • репродукция уч-ми полученных знаний, • основа – классно-урочная система; активная деятельность учителя и пассивная – учеников. 2) технология поэтапного форм-ния умств. действий (основная теория П.Я. Гальперина) включает: • осознание схемы основы действия, • непосредственное выполнение действия, • варианты более сложных действий, • переход от внешней формы изложения к внутренней, • любое полученное действие выполняется самостоятельно, т.е. умение переходит в навык. 3) технология коллективного взаимообучения (авторы А. Г. Ривин и В.К. Дьяченко): осн. умение уч-ля – сочетать коллективн. и инд. формы работы со шк-ми. Этапы: подготовительный (должны форм-ся умения ориентироваться в пространстве, умение слушать и слышать партнера, работать в шумовой среде, находить нужную информацию в доп. источниках, умение переводить образ в слово и слово в образ) и ознакомительный (общие правила игры, способы взаимодействия в группах), это обучение в подвижных парах, включает в себя взаимообучение и взаимоконтроль. 4) технология полного усвоения (Дж. Керолл и Б. Блум): цель – реорганизация классно-урочн. системы. Они пытаются достичь полного усвоения знаний всеми уч-ми. Контроль по двубальной системе (зачет-незачет). Ученик, который не справляется, должен иметь альтернативу. Ориентация на небольшие кол-вы и использование индивидуальных форм работы. 5) технология развивающего обучения (Л. Занков, Д. Эльконин, В. Давыдов, В. Репкин): При развивающем обучении учитываются: главные психологические новообразования данного возраста, которые возникают и развиваются в этом возрастном периоде; ведущая деятельность данного периода, определяющая возникновение и развитие соответствующих новообразований; содержание и способы совместного осуществления этой деятельности;взаимосвязи с другими видами деятельности;система методик, позволяющая определять уровни развития новообразований. Превращение ребенка в субъекта, заинтересованного в самоизменении и способного к нему, превращение ученика в учащегося. Обесп-е условий для такого превращения является осн. целью развив. обуч-я, которая принципиально отличается от цели традиц. школы – подготовить ребенка к выполнению тех или иных функций в обществ. жизни. Фундаментом структуры содерж-я каждого предмета является система понятий, которые исчерпывают основы данной науки. Введение этих понятий в обучение осуществляется в опред. последовательности, начиная с базовых понятий. (Напр, в рус. яз. обуч-е начинается с введения понятий «звук» – «буква» – «фонема», над которыми потом «надстраиваются» «слово» – «словосочетание» – «предложение» – «текст». Подобная система понятий и создает фундамент для изучения и оперирования любой лингвистической системой). В рез-те такого обучения у школьников формируется система понятий, которая определяет логику и развитие данной области знаний. Обучение осуществляется путем последовательной постановки перед ребенком ряда учебных задач, которые требуют усвоения понятий. Информация в готовом виде не подается. В процессе решения задачи ребенок сам организовывает свою познавательную и учебную деятельность, одновременно усваивая знания и разрабатывая собственные способы работы. Процесс разрешения задачи каждым ребенком включается в коллективную деятельность класса, которая, в конце концов, обеспечивает нахождение и усвоение оптимального для данной задачи обобщенного способа деят-ти. В своей учебной деят-ти ребенок находится в состоянии постоянной рефлексии: для него важно не только то, «что» я делаю, но и «как», «какими способами» я это делаю. Технология проблемно-модульного обучения (материал дается укрупненными блоками, составляются мини-учебники, исп-ся рейтинговые шкалы, оценки усвоения). Технология М. Монтессори (итал. педагог, кот. основала систему работы с детьми на идеях свободного воспитания). Ведущие пед. идеи: каждый ребенок от рождения наделен ему одному присущим потенциалом развития, кот. может быть реализован только в собственной дея-ти ребенка. Задача педагога – создать среду, облегчающую ребенку раскрытие собственного потенциала. Монтессори определила 3 этапа развития: 1) до 6 лет (период «впитывающего сознания», языкового, сенсомоторного развития. Педагог организует среду, в кот. нах-ся специальные материалы, с кот. ребенок развивает свою сенсорную сферу, формирует практич-е навыки); 2) от 6 до 9 лет (ребенок – исследователь, познает мир с помощью воображения); 3) от 9 до 12 лет (ребенок – ученый). Вместо классно-урочной системы – свободная работа детей в развивающей среде (рефлексивный и дидактический круги), погружение в отдельные области знаний на третьем году и творческие студии-мастерские. 86. Методика изучения геометрических тел в начальной школе. I. Точки, линии. Точка – неопределяемое понятие. Сталкиваются в подготовительный период при ознакомлении с клетчатой разлиновкой. Образное представление о точке – кончик карандаша, ручки оставляет след – это и ксть точка. Точками яв-ся концы отрезка, вершины многоугольника, центр окружности. Дети учатся обозначать точки буквами, проводить линии через точки. Прямая и кривая линии - неопределяемые понятия. Кривые линии бывают замкнутые и незамкнутые. Важно создать представление о бесконечной прямой Отрезок – часть прямой, ограниченная с двух сторон. отрезок не отрезок Дети учатся чертить отрезки, измерять их, сравнивать. Отрезками яв-ся стороны многоугольника, звенья ломаной, радиус, диаметр. * Если из точки провести по линейке прямую линию, то получим геом-ую ф-ру, которая называется ЛУЧ. * Если провести два луча из одной точки; то получим геом-ую ф-ру, которая называется УГЛОМ. Лучи стороны угла. Ломаная линия: звенья яв-ся отрезками, не лежат на одной прямой, конец одного отрезка яв-ся началом другого. Знакомятся с замкнутой (незамкнутой) ломаной; учатся чертить, находить длину ломаной. * Замкнутая ломаная линия яв-ся границей многоугольника. Угол имеет вершину и стороны (у Моро при знакомстве с многоугольниками). Дети легко справляются с построением угла. Но необходимо рассмотреть угол с точки зрения угла как плоскости, ограниченной двумя лучами. Необходимо проводить работу с моделями углов: Для получения модели прямого угла, выполняется практическая работа. Дети из листа с неровными краями и точкой посередине, путем складывания – первая линия сгиба д пройти через точку; далее сложить так, чтобы части линии сгиба совместились – получаем прямой угол Все модели, полученные учащимися накладываются друг на друга – вывод: все прямые углы равны м-у собой. При знакомстве с острым и тупым углом, используют модель 3-х углов. Если на модель прямого угла наложить модель острого угла так, чтобы одна сторона совместилась, то др сторона пройдет внутри прямого угла, а в случае наложения тупого угла, другая его сторона пройдет вне прямого угла. Все виды углов учащиеся выделяют на различных фигурах. Некоторые авторы дополнительно вводят градусную меру углов, знакомят с транспортиром. У Петерсон – развернутый, вертикальные и смежные углы. II. Имея представление о точке, отрезке, угле, уч-ся м находить эти геом-ие фигуры в треугольниках, четырехугольниках, пятиугольниках и т.д., называя все эти ф-ры – многоугольниками. Для упр-й в распознавании многоуг-ов м применять не только плоскостные фигуры, но и объемные тела – призмы, пирамиды. Работая с объемными телами уч-ся усваивают термины– грань, ребро, вершина (Истомина, Петерсон). Многоугольник рассматривается с точки зрения замкнутой ломаной и наз-ся по количеству углов и сторон. У всякого многоугольника есть вершины, стороны, углы. Для детей представляет трудность осознать что любой квадрат яв-ся прямоугольником. Причина в том, что образ квадрата и прямоугольника в сознании детей уже сформировался, а умением выделять существенные признаки еще не овладели. Прием - на доске различные фигуры: - Как их можно назвать? (многоугольники). – Назовите и покажите, у которой 3 угла и 3 стороны; 4 угла и 4 стороны; 5 углов и 5 сторон ит.д. Предложить оставить только 4-хугольники. Выделите те у которых один, два, три, четыре прямых угла. Через несколько попыток дети м догадаться, что фигуры с тремя прямыми углами не может быть. Все прямые углы проверяются с помощью модели прямого угла. В результате выделяются четырехугольники у которых все углы прямые. Они называются прямоугольники. Среди прямоугольников может выделить те, у которых все стороны равны. Это квадраты. Отношения м-у понятиями многоугольник, четырехугольник, квадрат можно представить схематично: КВАДРАТ ПРЯМОУГОЛЬНИКИ ЧЕТЫРЕХУГОЛЬНИКИ МНОГОУГОЛЬНИКИ Эту схему потом обыгрывают: «Где мое место?» Учащиеся должны уметь чертить квадрат и прямоугольник и находить периметр и площадь. Треугольник – дается описание, знакомятся с видами треугольников (класс по углам; разносторонние, равносторонние, равнобедренные). Круг и окружность – круг изучается в подготовительный период, используется как счетный материал. Окружность – граница круга. Чертим циркулем – центр окружности. Изучается центр окружности, радиус, диаметр. Учатся чертить окружности. Уточняется понятие круг. Объемные геометрические фигуры. Куб, шар… В новых стандартах – умение распознавать, различать, называть. Параллелепипед, цилиндр, конус – показать, найти в окружающем пространстве, познакомить с чертежами. Полезно давать развертки. Многие авторы предлагают развивающие упр (игры). Истомина - игра «Дай как можно больше названий фигуры» 1 2 3 1 – многоугольник, четырехугольник, трапеция. 2 - многоугольник, четырехугольник, прямоугольник, квадрат. 3 - многоугольник, четырехугольник, параллелограмм, ромб. Некоторые авторы вводят единицы объема; учат объем параллелограмма и куба. 87.Организация работы с крупнобъемным произведением в начальной школе. Учителю надо позаботиться о том, чтобы круг чтения был разнообразным, чтобы каждый смог выбрать то, что его больше интересует. Очень важно, чтобы книги были доступны и интересны детям данного возраста. Для поддержания устойчивого интереса важно научить детей выбирать нужную и полезную информацию, научить ориентироваться в книжном мире. Необходимо не только вызвать интерес, но и направить на то, что больше интересует данного ученика. При работе с крупнообъёмными произведениями мы выделили 3 этапа формирования типа правильной читательской деятельности: 1. Слушание-общение (1кл.). 2. Сочетание коллективного и самостоятельного чтения (2-3кл.). 3. Самостоятельное чтение (4кл.). Границы этих этапов условны и подвижны. На самостоятельный уровень чтения ученик может выйти и раньше 4 класса. На уроках внеклассного чтения подводится итоги прочитанного. Но главная работа заключается в подготовке к итоговому уроку. Знакомство с произведением идёт на основе использования методики коллективного чтения: чтение вслух, обсуждение, пересказ, обмен мнениями и т.д. Постепенно уровень самостоятельности повышается. К 4 классу дети должны выйти на уровень читательской самостоятельности, организовывать собственную читательскую деятельность по ознакомлению с большим по объёму произведением. Формирование читательской самостоятельности зависит от уровня знаний, умений и навыков (чем больше знаний, тем выше интерес). |
