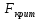 => =>  - отвергается, логарифмическая модель с - отвергается, логарифмическая модель с  значима при α= 0,1. значима при α= 0,1.
Данная модель удобна тем, что коэффициенты 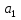 и и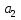 при логарифме объясняющей переменной выражает эластичность переменной p по переменным при логарифме объясняющей переменной выражает эластичность переменной p по переменным 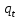 и и  . В нашем случае эластичность при . В нашем случае эластичность при 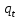 равна 0,470, а при равна 0,470, а при  равна 0,234. То есть изменение объема в данный период и изменение объема в предыдущем периоде не оказывает особого влияния. равна 0,234. То есть изменение объема в данный период и изменение объема в предыдущем периоде не оказывает особого влияния.
Таким образом, анализ показал, что логарифмическая модель с  значима, а также статистическую значимость значима, а также статистическую значимость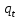 и статистическую не значимость и статистическую не значимость  параметров уравнения регрессии. Однако, теснота логарифмической связи не достаточна, чтобы признать данную модель приемлемой, а тем более хорошей. параметров уравнения регрессии. Однако, теснота логарифмической связи не достаточна, чтобы признать данную модель приемлемой, а тем более хорошей.
С ноября 2013 года по март 2014 года по формуле (1) параметры модели равны: 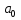 = 22,495, = 22,495, 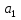 = -0,526, = -0,526, 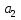 = -1,048. Следовательно, модель выглядит следующим образом: = -1,048. Следовательно, модель выглядит следующим образом: 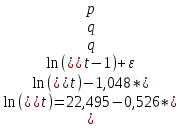 . С помощью этой модели находим новую цену и остатки (прил. 9). . С помощью этой модели находим новую цену и остатки (прил. 9).
В нашей модели коэффициент детерминации равен 21,5%, на столько процентов вариация равновесных объёмов объясняется вариацией равновесных цен.
Далее осуществим проверку гипотезы о значимости регрессора, с помощью т – статистики. Путь гипотеза  – регрессор не значим: – регрессор не значим:
Задаем уровень значимости: α= 0,05
Найдем t наблюдаемое по формуле (3): 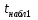 = 2,621, = 2,621,  = 5,235 = 5,235
Найдем t критическое по формуле (4): 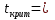 1,963 1,963
Сравниваем: 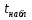 > >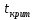 => гипотеза => гипотеза  – отвергается, для – отвергается, для 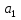 , ,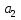 при α= 0,05 => регрессоры при α= 0,05 => регрессоры 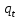 , ,  –значимы. –значимы.
Последний шаг в анализе – это проверка гипотезы о значимости модели. Гипотеза  : : 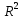 =0 – модель не значима: =0 – модель не значима:
Задаем уровень значимости: α= 0,01
Находим эмпирическое значение по формуле (6): 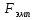 = 120,887 = 120,887
Находим критическое значение по формуле (7): 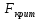 = 4,629 = 4,629
Сравниваем: 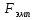 > >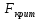 => =>  - отвергается, логарифмическая модель с - отвергается, логарифмическая модель с  значима при α= 0,01. значима при α= 0,01.
Эластичность при 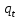 равна 0,526, а при равна 0,526, а при  равна 1,048. То есть изменение объема в данный период не оказывает влияние на изменение равновесных цен, а изменение объема в предыдущем периоде оказывает влияние на изменение равновесных цен электроэнергии. равна 1,048. То есть изменение объема в данный период не оказывает влияние на изменение равновесных цен, а изменение объема в предыдущем периоде оказывает влияние на изменение равновесных цен электроэнергии.
Таким образом, анализ показал, что логарифмическая модель с  значима, а также статистическую значимость параметра уравнения регрессии. Однако, теснота логарифмической связи не достаточна, чтобы признать данную модель приемлемой, а тем более хорошей. значима, а также статистическую значимость параметра уравнения регрессии. Однако, теснота логарифмической связи не достаточна, чтобы признать данную модель приемлемой, а тем более хорошей.
С ноября 2014 года по март 2015 года по формуле (1) параметры модели равны: 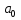 = -6,657, = -6,657, 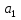 = 1,533, = 1,533, 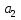 = -0,226. Следовательно, модель выглядит следующим образом: = -0,226. Следовательно, модель выглядит следующим образом: 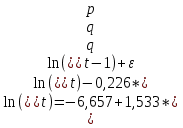 . С помощью этой модели находим новую цену и остатки (прил. 9). . С помощью этой модели находим новую цену и остатки (прил. 9).
В нашей модели коэффициент детерминации равен 24,1%, на столько процентов вариация равновесных объёмов объясняется вариацией равновесных цен.
Далее осуществим проверку гипотезы о значимости регрессора, с помощью т – статистики. Путь гипотеза  – регрессор не значим: – регрессор не значим:
Задаем уровень значимости: α= 0,1
Найдем t наблюдаемое по формуле (3): 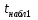 = 12,014, = 12,014,  = 1,777 = 1,777
Найдем t критическое по формуле (4): 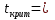 1,666 1,666
Сравниваем: 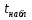 > >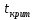 => гипотеза => гипотеза  – отвергается, для – отвергается, для 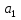 , ,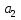 при α= 0,1 => регрессоры при α= 0,1 => регрессоры 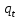 , ,  –значимы. –значимы.
Последний шаг в анализе – это проверка гипотезы о значимости модели. Гипотеза  : : 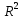 =0 – модель не значима: =0 – модель не значима:
Задаем уровень значимости: α= 0,01
Находим эмпирическое значение по формуле (6): 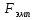 = 140,551 = 140,551
Находим критическое значение по формуле (7): 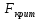 = 2,309 = 2,309
Сравниваем: 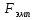 < <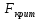 => =>  - принимается, логарифмическая модель с - принимается, логарифмическая модель с  не значима при α= 0,01. не значима при α= 0,01.
Эластичность при 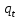 равна 1,533, а при равна 1,533, а при  равна 0,226. То есть изменение объема в данный период оказывает влияние на изменение равновесных цен электроэнергии, а изменение объема в предыдущем периоде не оказывает особого влияния на изменение равновесных цен электроэнергии. равна 0,226. То есть изменение объема в данный период оказывает влияние на изменение равновесных цен электроэнергии, а изменение объема в предыдущем периоде не оказывает особого влияния на изменение равновесных цен электроэнергии.
Таким образом, анализ показал, что логарифмическая модель с  значима, а также статистическую значимость параметра уравнения регрессии. Однако, теснота логарифмической связи не достаточна, чтобы признать данную модель приемлемой, а тем более хорошей. значима, а также статистическую значимость параметра уравнения регрессии. Однако, теснота логарифмической связи не достаточна, чтобы признать данную модель приемлемой, а тем более хорошей.
В 2015 году по формуле (1) параметры модели равны: 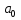 = 1,432, = 1,432, 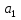 = 0,733, = 0,733, 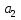 = -0,230. Следовательно, модель выглядит следующим образом: = -0,230. Следовательно, модель выглядит следующим образом: 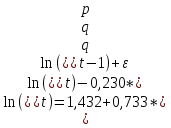 . С помощью этой модели находим новую цену и остатки (прил. 9). . С помощью этой модели находим новую цену и остатки (прил. 9).
В нашей модели коэффициент детерминации равен всего 1,5%, на столько процентов вариация равновесных объёмов объясняется вариацией равновесных цен.
Далее осуществим проверку гипотезы о значимости регрессора, с помощью т – статистики. Путь гипотеза  – регрессор не значим: – регрессор не значим:
Задаем уровень значимости: α= 0,1
Найдем t наблюдаемое по формуле (3): 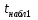 = 2,052, = 2,052,  = 0,644 = 0,644
Найдем t критическое по формуле (4): 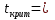 1,649 1,649
Сравниваем: 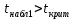 => гипотеза => гипотеза  – отвергается, для – отвергается, для 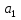 при α= 0,1 => регрессор при α= 0,1 => регрессор 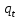 – значим. – значим.  < <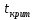 => гипотеза => гипотеза  – принимается, для – принимается, для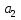 при α= 0,1 => регрессоры при α= 0,1 => регрессоры  – не значим. – не значим.
Последний шаг в анализе – это проверка гипотезы о значимости модели. Гипотеза  : : 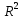 =0 – модель не значима: =0 – модель не значима:
Задаем уровень значимости: α= 0,1
Находим эмпирическое значение по формуле (6): 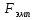 = 2,437 = 2,437
Находим критическое значение по формуле (7): 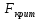 = 2,309 = 2,309
Сравниваем: 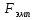 > >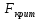 => =>  - отвергается, логарифмическая модель с - отвергается, логарифмическая модель с  значима при α= 0,1. значима при α= 0,1.
Эластичность при 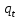 равна 0,733, а при равна 0,733, а при  равна 0,230. То есть изменение объема в данный период и изменение объема в предыдущем периоде не оказывает большого влияния на изменение равновесных цен электроэнергии. равна 0,230. То есть изменение объема в данный период и изменение объема в предыдущем периоде не оказывает большого влияния на изменение равновесных цен электроэнергии.
Таким образом, анализ показал, что логарифмическая модель с  значима, а также статистическую значимость значима, а также статистическую значимость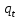 и статистическую не значимость и статистическую не значимость  параметров уравнения регрессии. Однако, теснота логарифмической связи не достаточна, чтобы признать данную модель приемлемой, а тем более хорошей. параметров уравнения регрессии. Однако, теснота логарифмической связи не достаточна, чтобы признать данную модель приемлемой, а тем более хорошей.
В общей модели по формуле (1) параметры модели равны: 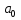 = -4,482 = -4,482 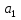 = 1,076, = 1,076, 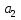 = 0,014. Следовательно, модель выглядит следующим образом: = 0,014. Следовательно, модель выглядит следующим образом: 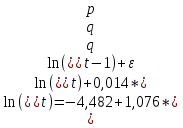 . С помощью этой модели находим новую цену и остатки (прил. 9). . С помощью этой модели находим новую цену и остатки (прил. 9).
В нашей модели коэффициент детерминации равен всего 5,6%, на столько процентов вариация равновесных объёмов объясняется вариацией равновесных цен.
Далее осуществим проверку гипотезы о значимости регрессора, с помощью т – статистики. Путь гипотеза  – регрессор не значим: – регрессор не значим:
Задаем уровень значимости: α= 0,1
Найдем t наблюдаемое по формуле (3): 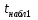 = 6,650, = 6,650,  = 0,085 = 0,085
Найдем t критическое по формуле (4): 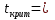 1,645 1,645
Сравниваем: 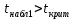 => гипотеза => гипотеза  – отвергается, для – отвергается, для 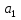 при α= 0,1 => регрессор при α= 0,1 => регрессор 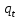 – значим. – значим.  < <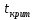 => гипотеза => гипотеза  – принимается, для – принимается, для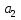 при α= 0,1 => регрессоры при α= 0,1 => регрессоры  – не значим. – не значим.
Последний шаг в анализе – это проверка гипотезы о значимости модели. Гипотеза  : : 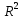 =0 – модель не значима: =0 – модель не значима:
Задаем уровень значимости: α= 0,01
Находим эмпирическое значение по формуле (6): 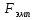 = 75,625 = 75,625
Находим критическое значение по формуле (7): 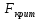 = 4,629 = 4,629
Сравниваем: 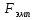 > >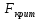 => =>  - отвергается, логарифмическая модель с - отвергается, логарифмическая модель с  значима при α= 0,01. значима при α= 0,01.
Эластичность при 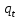 равна 1,076, а при равна 1,076, а при  равна 0,014. То есть изменение объема в данный период оказывает влияние на изменение равновесных цен электроэнергии, а изменение объема в предыдущем периоде не оказывает большого влияния на изменение равновесных цен электроэнергии. равна 0,014. То есть изменение объема в данный период оказывает влияние на изменение равновесных цен электроэнергии, а изменение объема в предыдущем периоде не оказывает большого влияния на изменение равновесных цен электроэнергии.
Таким образом, анализ показал, что логарифмическая модель с  значима, а также статистическую значимость значима, а также статистическую значимость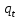 и статистическую не значимость и статистическую не значимость  параметров уравнения регрессии. Однако, теснота логарифмической связи не достаточна, чтобы признать данную модель приемлемой, а тем более хорошей. параметров уравнения регрессии. Однако, теснота логарифмической связи не достаточна, чтобы признать данную модель приемлемой, а тем более хорошей. |
 Скачать 0.5 Mb.
Скачать 0.5 Mb.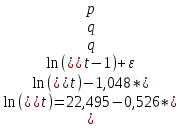 . С помощью этой модели находим новую цену и остатки (прил. 9).
. С помощью этой модели находим новую цену и остатки (прил. 9). 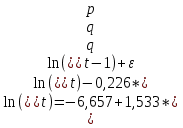 . С помощью этой модели находим новую цену и остатки (прил. 9).
. С помощью этой модели находим новую цену и остатки (прил. 9). 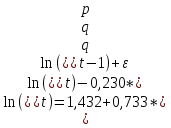 . С помощью этой модели находим новую цену и остатки (прил. 9).
. С помощью этой модели находим новую цену и остатки (прил. 9). 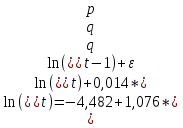 . С помощью этой модели находим новую цену и остатки (прил. 9).
. С помощью этой модели находим новую цену и остатки (прил. 9). 