СБОРНИК ПРАКТИЧЕСКИХ РАБОТ по дисциплине «КОМПЬЮТЕРНОЕ МОДЕЛИРОВ. Братский целлюлознобумажный колледж федерального государственного бюджетного образовательного учреждения
 Скачать 2.25 Mb. Скачать 2.25 Mb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ БРАТСКИЙ ЦЕЛЛЮЛОЗНО-БУМАЖНЫЙ КОЛЛЕДЖ ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО БЮДЖЕТНОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ ВЫСШЕГО ОБРАЗОВАНИЯ «БРАТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ» Специальность 15. 02.07 Автоматизация технологических процессов и производств (по отраслям) СБОРНИК ПРАКТИЧЕСКИХ РАБОТ по дисциплине «КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ» Братск 2017 Составила (разработала) Усанина Н.Ю., преподаватель кафедры ИСПиА Рассмотрено на заседании кафедры ИСПиА «_____»_____________20__г. _______________________ Одобрено и утверждено редакционным советом ____________________ «_____»_____________20__г. №_____________________ Содержание Ведение 4 1 Математическое моделирование 5 1.1 Практическая работа № 1 5 1.2 Практическая работа № 2 8 1.3 Практическая работа № 3 15 1.4 Практическая работа № 4 22 1.5 Практическая работа № 5 25 1.6 Практическая работа № 6 26 1.7 Практическая работа № 7 34 2 Графическое моделирование 38 2.1 Практическая работа № 8 38 2.2 Практическая работа № 9 50 2.3 Практическая работа № 10 54 2.4 Практическая работа № 11 60 2.5 Практическая работа № 12 68 Заключение 73 Список использованных источников 74 Введение Сборник практических работ по дисциплине «Компьютерное моделирование» разрабатывалось на основе требований ФГОС СПО с опорой на научные принципы формирования содержания образования. Данное пособие отражает актуальные направления подготовки специалистов по специальности «15.02.07 Автоматизация технологический процессов и производств (по отраслям)» в области трехмерного компьютерного моделирования в Компас–3D и решения задач оптимизационного и имитационного моделирования в MS Excel. В практических работах, приведенных в пособии, содержатся как задания с подробными указаниями к выполнению, так и задания без алгоритма работы. Таким образом, предлагаемые практические работы можно использовать как для индивидуальной работы студентов на занятиях под руководством преподавателя, так и для самостоятельной работы обучающихся. Сборник содержатся задания для освоения основных приемов работы с программой Компас-3D: работа с интерфейсом системы, создание графических примитивов, работа с видами чертежа, построение сопряжений, работа с массивом элементов, разработка и редактирование трехмерных моделей различных тел. Используя данные методические указания Microsoft Excel и имеющиеся навыки работы, пользователь может создать шаблон, являющийся в итоге электронной моделью реального социально-экономического процесса. Материал изложен в соответствии с этапами экономико-математического моделирования, то есть сначала идет экономическая формулировка задачи, затем ее математическая формализация, затем компьютерная модель, затем интерпретация полученных результатов. 1 Математическое моделирование 1.1 Практическая работа 1 Оптимизационное моделирование в Excel Цель урока: построить информационную, математическую и компьютерную модели экономической задачи. Оборудование: персональный компьютер (ПК), программное обеспечение (ПО) Порядок выполнения и форма отчетности Рассмотрим пример. Фирма производит две модели А и В сборных книжных полок. Их производство ограничено наличием сырья (высококачественных досок) и временем машинной обработки. Для каждого изделия модели А требуется 3 м2 досок, а для изделия модели В – 4 м2. Фирма может получать от своих поставщиков до 1700 м2 досок в неделю. Для каждого изделия модели А требуется 12 мин машинного времени, а для изделия модели В – 30 мин. В неделю можно использовать 160 ч машинного времени. Сколько изделий каждой модели следует выпускать фирме в неделю, еcли каждое изделие модели А приносит 2 долл. прибыли, а каждое изделие модели В – 4 долл. прибыли? Компьютерная модель. Решение задачи в Excel. 1. Создайте новую рабочую книгу, сохраните ее под именем Chll.xls в своей папке. 2. Дайте первому листу имя "Полки". 3. Введите в ячейки рабочего листа информацию (рисунок 1). Ячейкам В2 и ВЗ присвойте имена х и у. В ячейках С6, С9 и С10 представлены формулы, занесенные в соответствующие ячейки столбца В. 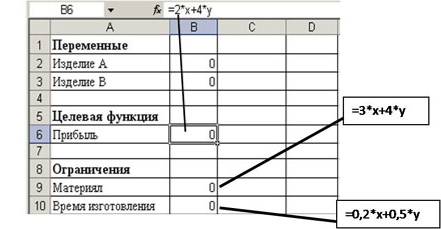 Рисунок 1 – Создание таблицы и заполнение ее формулами 4. выделите ячейку (B6), в которой вычисляется целевая функция, и вызовите Решатель ("Сервис/ Поиск решения"). В диалоговом окне в поле ввода "Установить целевую ячейку:" уже содержится адрес ячейки с целевой функцией $В$6. 5. Установите переключатель: "Равной максимальному значению"; 6. Перейдите к полю ввода "Изменяя ячейки:". В нашем случае достаточно щелкнуть кнопку "Предположить" и в поле ввода появится адрес блока $В$2:$В$3. 7. Перейдите к вводу ограничений. Щелкнем кнопку "Добавить". Появится диалоговое окно "Добавление ограничения". 8. Поле ввода "Ссылка на ячейку:" укажите $В$9. 9. Правее расположен выпадающий список с условными операторами (раскройте его и посмотрите). Выберем условие <=; 10. В поле ввода "Ограничение:" введите число 1700. (Рисунок 2) 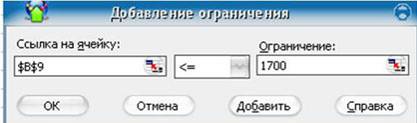 Рисунок 2 – Ввод ограничений 11. Есть еще одно ограничение, поэтому, не выходя из этого диалогового окна, щелкнем кнопку "Добавить"(в соответствии с рисунком 3) и введем ограничение $В$10<=160. 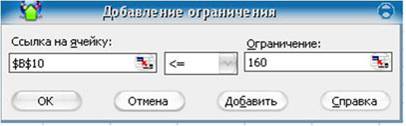 Рисунок 3 –Добавление ограничений 12. Ввод ограничений закончен, поэтому нажмем "ОК". 13. Вновь окажемся в диалоговом окне "Поиск решения". Увидим введенные ограничения $В$10<=160 и $В$9<=1700. Справа имеются кнопки "Изменить" и "Удалить". С их помощью можем изменить ограничение или стереть его в соответствии с рисунком 4. 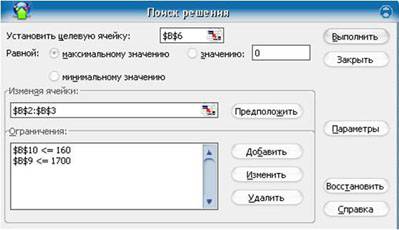 Рисунок 4 –Поиск решения 14. Щелкните кнопку "Параметры". Окажемся в диалоговом окне "Параметры поиска решения". Чтобы узнать назначение полей ввода этого окна, щелкнем кнопку "Справка". Менять ничего не будем, только установим два флажка: "Линейная модель" (так как наши ограничения и целевая функция являются линейными по переменным х и у) и "Неотрицательные значения" (для переменных х и у). Щелкнем "ОК" и окажемся в исходном окне. Самостоятельно добавьте ограничения, что переменная X и Y – целые Одним из таких инструментов является Поиск решения, который особенно удобен для решения так называемых "задач оптимизации". Если Вы раньше не использовали Поиск решения, то Вам потребуется установить соответствующую надстройку; 15. Полностью подготовив задачу оптимизации. Нажимаем кнопку "Выполнить". 16. Появляется диалоговое окно "Результаты поиска решения". В нем читаем сообщение "Решение найдено. Все ограничения и условия оптимальности выполнены." На выбор предлагаются варианты: "Сохранить найденное решение" или "Восстановить исходные значения". Выбираем первое. Можно также вывести отчеты: по результатам, по устойчивости, по пределам. Выделим их все, чтобы иметь представление о том, какая информация в них размещена. 17. После нажатия "ОК." вид таблицы меняется: в ячейках х и у появляются оптимальные значения. Числовые данные примера специально подобраны, поэтому в ответе получились круглые цифры: изделие А нужно выпускать в количестве 300 штук в неделю, а изделие В – 200 штук. Соответственно пересчитываются все формулы. Целевая функция достигает значения 1400, как показано на рисунке 5. 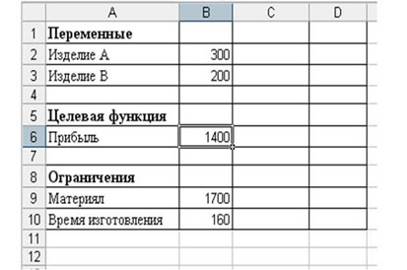 Рисунок 5 –Значение целевой функции Содержание отчета: название работы; цель работы; задание; результаты выполнения; вывод по работе. 1.2 Практическая работа 2 Оптимизационное моделирование в Excel Цель урока: закрепить алгоритм моделирования на примере построения компьютерной модели реальной экономической задачи “Штатное расписание больницы ”. Оборудование: персональный компьютер (ПК), программное обеспечение (ПО) Порядок выполнения и форма отчетности Оптимизационное моделирование – это поиск оптимального, т.е. наилучшего решения конкретной задачи при выполнении некоторых заданных условий. Критерием оптимальности могут быть различные параметры, например, максимальное количество выпускаемой продукции, максимальная прибыль фирмы, минимальные затраты производства. При решении задач оптимизационного моделирования на компьютере рекомендуется руководствоваться следующим алгоритмом: разобрать условие задачи; на основе исходных данных построить математическую модель задачи: определить изменяемые (поисковые) переменные; задать ограничения; выбрать целевую функцию (критерий оптимизации). решить задачу на компьютере с помощью программы MS Excel; проанализировать полученные данные. Перед началом работы в MS Excel необходимо убедиться, что надстройка «Поиск решения» установлена. В Excel 2003: в меню «Сервис» имеется пункт «Поиск решения». Если его нет, нужно установить эту надстройку: в меню «Сервис» – «Надстройки» – устанавливаем флажок «Поиск решения». В Excel 2007: «Данные» - «Анализ» - «Поиск решения». Если его нет, нужно установить. Чтобы активизировать ее в Excel 2007, щелкните значок Кнопка Microsoft Office , щелкните Параметры Excel, а затем выберите категорию Надстройки. В поле Управление выберите значение Надстройки Excel и нажмите кнопку Перейти. В поле Доступные надстройки установите флажок рядом с пунктом Поиск решения и нажмите кнопку ОК. Рассмотрим решение задачи на оптимизацию на конкретном примере. Задача. Цех молокозавода выпускает эскимо и другой вид мороженого (назовем его просто «мороженое»). Эскимо в 2 раза дороже мороженого. За одну минуту выпускается 90 порций мороженого или 30 порций эскимо, возможен одновременный выпуск двух видов продукции. Из-за ограничения срока реализации продукции и недостаточного объема холодильных камер в течение часа на хранение может быть принято не более 3600 шт. изделий. Определить наибольшую стоимость выпускаемой продукции (прибыль) и оптимальный план выпуска мороженого и эскимо за одну минуту. Построим математическую модель решения данной задачи. Пусть одновременно выпускается 2 вида продукции. Обозначим число выпускаемых за 1 мин. эскимо – х, мороженого – у. Пусть: t1 – время, необходимое для производства одного эскимо, t2 - время, необходимое для производства одного мороженого. Из условия задачи следует, что за 1 мин. производится 90 порций мороженого или 30 порций эскимо, т.о. времени на производство одного эскимо затрачивается в 3 раза больше, чем на производство одного мороженого: t1=3 t2 За 1 мин. соотношение времени при одновременном выпуске каждого из двух видов продукции х и у составит: t1х + t2у≤1 или, подставляя t1=3 t2 получим 3t2х + t2у≤1 вынесем t2 за скобки и разделим на него левую и правую части уравнения, т.о. 3х+у≤1/t2 Но величина 1/t2 – это максимальный выпуск мороженого за 1 мин., т.е. она равна 90. Итак, возможности производства определяет условие: 3х+у≤ 90 Еще одно условие - ограниченная емкость холодильника. В течение 1 часа холодильник может принять 3600 шт. продукции, т.е. за одну минуту 3600/60=60 порций: х+у≤60 Обозначив цену 1 эскимо - с1 (руб), а цену мороженого – с2 (руб), можно записать в соответствии с условием задачи следующее соотношение цен на продукцию с1=2с2 Общая стоимость продукции, выпускаемой цехом за 1 минуту: S= с1х+ с2у, заменяя с1=2с2 получим S=2с2х+ с2у= с2(2х+у) Поскольку с2 – заданная положительная константа, то для упрощения задачи можно принять с2=1. По условию задачи необходимо найти наибольшую возможную стоимость выпускаемой продукции. Т.о. следует добиваться максимального значения целевой функции S=2х+у. Обязательным условием решения задачи является условие неотрицательности величин х и у. Следует также подчеркнуть, что в целом ряде задач, в т.ч. и нашей, необходимо ввести еще одно ограничение: решение должно быть целочисленным. Итак, учитывая все условия задачи, приходим к ее математической модели: среди целочисленных решений системы линейных неравенств 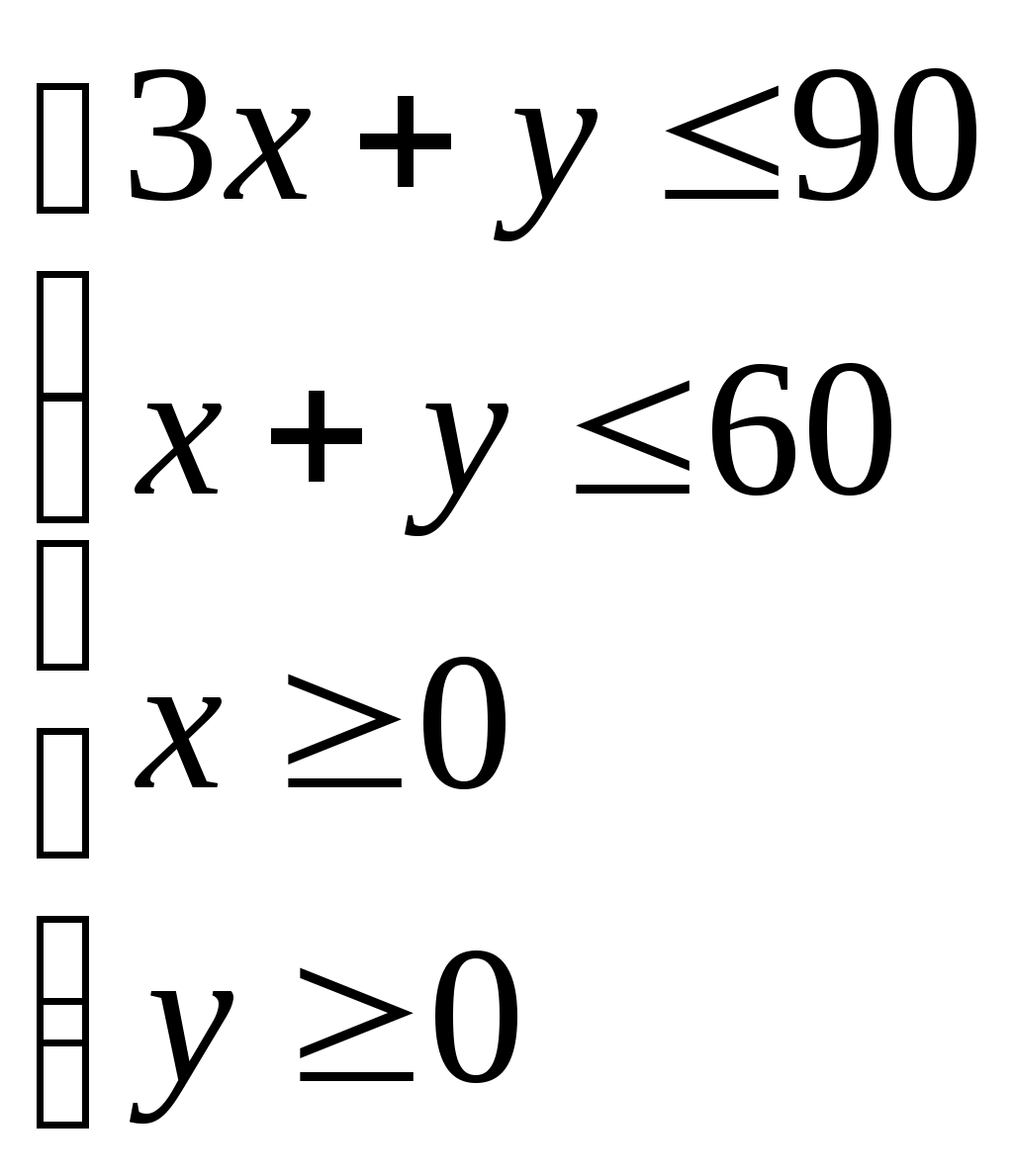 найти такое, при котором достигается максимизация линейной функции: S=2х+у. Решение задачи на компьютере: Запустите MS Excel. В 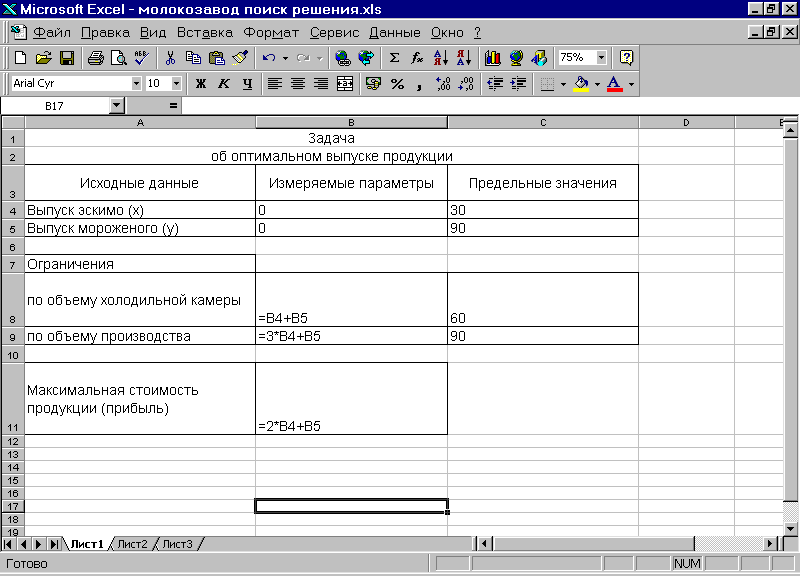 новой рабочей книге оформите лист в соответствии с рисунком 6. Рисунок 6 –Оформление листа в соответствии с задачей В описанной модели необходимо максимизировать значение в ячейке В11. В качестве начальных значений х и у принимаются нули. Ограничения задачи представлены в таблице 1. Таблица 1– Условия ограничений на значение
Дальнейшее решение задачи будем осуществлять с помощью надстройки «Поиск решения». Выделите ячейку с оптимизируемым значением В11. Выберите надстройку Поиск решения. Загрузится надстройка и появляется диалоговое окно «Поиск решения» (рисунок 7). 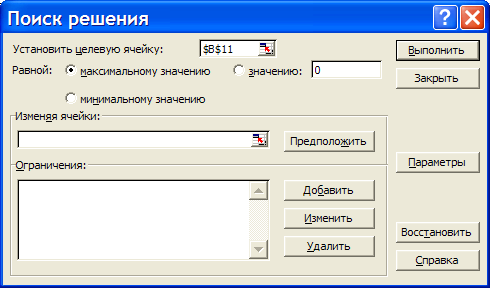 Рисунок 7 – Поиск решения В поле «Установить целевую ячейку» уже находится ссылка на выделенную на предыдущем шаге ячейку (при необходимости эту ссылку можно изменить). Установить переключатель «Равной» максимальному значению (ищется максимальное значение целевой ячейки В11). Перейдите в поле «Изменяя ячейки:» и укажите диапазон ячеек, которые должны изменяться в процессе поиска наилучшего решения. В данном примере это ячейки $B$4:$B$5. Щелкните по кнопке «Добавить», чтобы ввести первое ограничение задачи. Откроется диалоговое окно «Добавление ограничения» (рисунок 8). 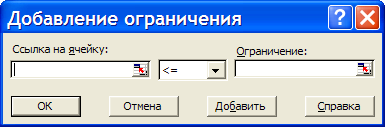 Рисунок 8 –Диалоговое окно «Добавления ограничения» Введите первое ограничение $B$4:$B$5>=0. Щелкните по кнопке «Добавить», введите следующее ограничение и т.д. из таблицы на предыдущей странице. Примечание: для задания целочисленности значений ячеек В4 и В5 из второго раскрывающегося списка выберите «цел», при этом в поле «Ограничение» автоматически появится «целое». После ввода последнего ограничения нажмите ОК. Окно поиск решения примет вид (рисунок 9) 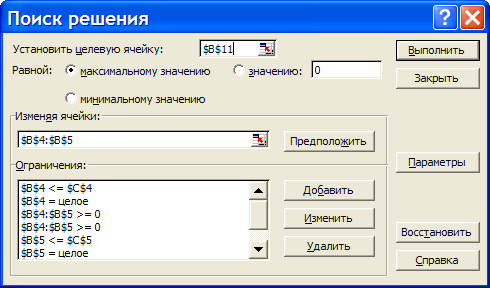 Рисунок 9 – Окно «Поиск решения» Нажав на кнопку «Параметры можно проверить, и при необходимости, изменить условия и варианты поиска решения, что в нашей задаче не требуется. Нажмите кнопку «Выполнить». По окончании поиска решения появится диалоговое окно результатов (рисунок 10). 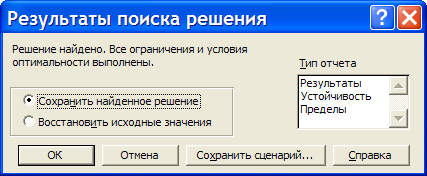 Рисунок 10 – Диалоговое окно «Результаты поиска решения» Установите переключатель «Сохранить найденное решение», чтобы сохранить предложенные значения. С помощью этого диалогового окна можно также сформировать отчет; Н 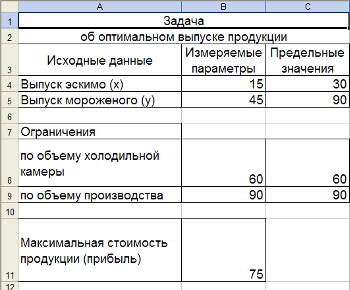 ажмите ОК. Получится решение, представленное на рисунке 11. Рисунок 11 – Результат поиска решения Сохраните решение задачи в своей папке под именем МОЛОКОЗАВОД. Дополнительные задания к этой задаче: предположим, что цех получил дополнительную холодильную установку, холодильник может принять не 60, а 110 порций продукции за 1 минуту. Определите, поможет ли ликвидация этого «узкого места» увеличить прибыль; увеличить прибыль можно ничего не изменяя в организации производства, а просто увеличив цены на продукцию. Например, пусть цена эскимо будет не в два, а в 2,5 раза больше, чем цена мороженого. Предполагаемая прибыль увеличится, но найдет ли спрос более дорогая продукция? Задача №1. Представьте, что вас выбрали директором завода и вы, изучив спрос, решили организовать участок для производства двух товаров широкого потребления – мясорубки и скороварки (А и Б). Допустим, что вам удалось заключить договор со смежниками на поставку ресурсов (металла, электроэнергии и т.п.) и выделить определенное число рабочих. Чтобы обеспечить рентабельность участка, Совет трудового коллектива установил план по реализации, указывающий минимальные объемы производства для каждого изделия. Всякий хороший директор стремиться к тому, чтобы прибыль была наибольшей. Условие задачи. На участке работает 20 человек, каждый из них в среднем за год работает 1800 часов. Выделенные ресурсы: 32 т металла, 54 тыс. квт.ч. электроэнергии. План по реализации: не менее 2 тыс. изделий А и не менее 3 тыс. изделий Б. На выпуск 1 тыс. изд. А затрачивается 3 т металла, 3 тыс. квт.ч. электроэнергии и 3 тыс. часов рабочего времени. На выпуск 1 тыс. изд. Б - 1 т металла, 6 тыс. квт.ч. электроэнергии и 3 тыс. часов рабочего времени. От реализации 1 тыс. изд. А завод получает прибыль 50 тыс. руб., а от реализации 1 тыс. изд. Б – 70 тыс. руб. Выпуск какого количества изделий А и Б (в тыс. шт.) надо запланировать, чтобы прибыль от их реализации была наибольшей. Математическая модель данной задачи.. Пусть х – планируемое количество изделий А (тыс. шт.) у – планируемое количество изделий Б(тыс. шт.). План по реализации: х≥2 и у≥3 Общий расход металла: 3х+у ≤ 32 Общий расход электроэнергии х+6у ≤ 54 Ограничение на ресурсы рабочего времени 3х+3у ≤ 36 Прибыль от реализации 50х+70у ЗАДАНИЕ Запустите MS Excel. На основе разработанной математической модели введите в новой рабочей книге все необходимые данные. С помощью команды Сервис – Поиск решения загрузите надстройку. С помощью диалогового окна «Поиск решения» получите требуемые результаты и сохраните найденное решение. Сохраните решение задачи в своей папке под именем УЧАСТОК. Задача №2. Какие размеры должен иметь бак объемом V=abh=2000 см3, чтобы на его изготовление пошло как можно меньше материала? Сторона а должна быть не меньше 10 см. Самостоятельно разработайте математическую модель данной задачи. Запустите MS Excel. На основе разработанной математической модели введите в новой рабочей книге все необходимые данные. С помощью команды Сервис – Поиск решения загрузите надстройку. С помощью диалогового окна «Поиск решения» получите требуемые результаты и сохраните найденное решение. Сохраните решение задачи в своей папке под именем БАК Задача №3. Фирма производит две модели А и Б сборных книжных полок. Их производство ограничено наличием сырья (высококачественных досок) и временем машинной обработки. Для каждого изделия модели А требуется 3 м2 досок, а для изделия модели Б – 4 м2. Фирма может получать от своих поставщиков до 1700 м2 досок в неделю. Для каждого изделия модели А требуется 12 мин. машинного времени, а для изделия модели Б – 30 мин. В неделю можно использовать 160 ч машинного времени. Сколько изделий каждой модели следует выпускать фирме в неделю, если каждое изделие модели А приносит 2$ прибыли, а каждое изделие модели Б – 4$ прибыли? Самостоятельно разработайте математическую модель данной задачи. Запустите MS Excel. На основе разработанной математической модели введите в новой рабочей книге все необходимые данные. С помощью команды Сервис – Поиск решения загрузите надстройку. С помощью диалогового окна «Поиск решения» получите требуемые результаты и сохраните найденное решение. Сохраните решение задачи в своей папке под именем ПОЛКИ. |
