теория цифровой экономики. вся теория3. Цифровое государство цифровое и электронное государство, электронное правительство
 Скачать 7.61 Mb.
|
|
3.4. Решение задач машинного обучения Задача классификации сводится к распределению объектов выборки по n категориям на основании набора признаков. Следует отметить, что множество объектов, классовая принадлежность которых заранее известна, называется обучающей выборкой. Решением задачи классификации называют построение алгоритма, способного классифицировать произвольный объект на основании множества признаков, классовая принадлежность которого заранее неизвестна. Примером задачи классификации может служить категоризация набора данных видов растений и животных на основании знаний, извлеченных из обучающей выборки. Задача регрессии представляет собой прогнозирование некоторого числового значения, на основании набора признаков. Перед алгоритмом ставится задача построения функции f: Rn R. Принципиальное отличие этого класса задач от задачи классификации заключается в типе прогнозируемой переменной. Примерами задач регрессии являются прогнозирование цен акций на бирже ценных бумаг и прогнозирование выручки торговой точки в следующем периоде. Задача кластеризации представляет собой распределение объектов выборки на основании набора признаков по n категориям, которые ранее не были определены. При решении задачи кластеризации алгоритм обрабатывает неразмеченный набор данных, разбивая выборку на непересекающиеся группы (кластеры). Примером задачи кластеризации может служить категоризация потребителей по степени заинтересованности группами товаров. Задача выявления аномалий сводится к просмотру набора признаков, описывающих объекты выборки на предмет выявления нетипичного значения/сочетания значений одного или нескольких признаков. Примером задачи выявления аномалий являются задачи связанные с мониторингом состояния оборудования, подозрительной активности, связанной с нетипичными финансовыми операциями банковского счета. Уменьшение размерности – это уменьшение числа признаков, описывающих объекты выборки. Согласно литературным данным, в некоторых случаях анализ данных, такой как регрессия или классификация, может быть осуществлён в редуцированном пространстве более точно, чем в исходном пространстве. Для решения вышеперечисленных задач применяются различные аналитические алгоритмы: Деревья принятия решений, случайный лес, KNN (метод k ближайших соседей), линейная и логистическая регрессии, метод опорных векторов, PCA (метод главных компонент), ICA (анализ независимых компонент), сингулярное разложение, CART и многие другие. Методы машинного обучения «с учителем» Алгоритмы машинного обучения «с учителем» решают аналитические задачи, которые подразумевают необходимость наличия обучающей выборки. Обучающей выборкой в данном случае является размеченный набора данных, для которого заранее известна целевая переменная (прогнозируемый параметр). Задача обучения «с учителем» сводится к задаче ассоциации некоторого «ввода» с некоторыми вариантами «вывода». Примером такой задачи может служить задача построения модели классификации растений, обученной на основании обучающей выборки, в которой каждый случай измерений заранее ассоциирован с конкретным видом растения. Методы машинного обучения «без учителя» Алгоритмы машинного обучения «без учителя» решают аналитические задачи, связанные с изучением структуры и свойств собранного набора данных. Такой набор данных является неразмеченным, другими словами, в нем отсутствуют данные о целевой переменной. Деревья принятия решений 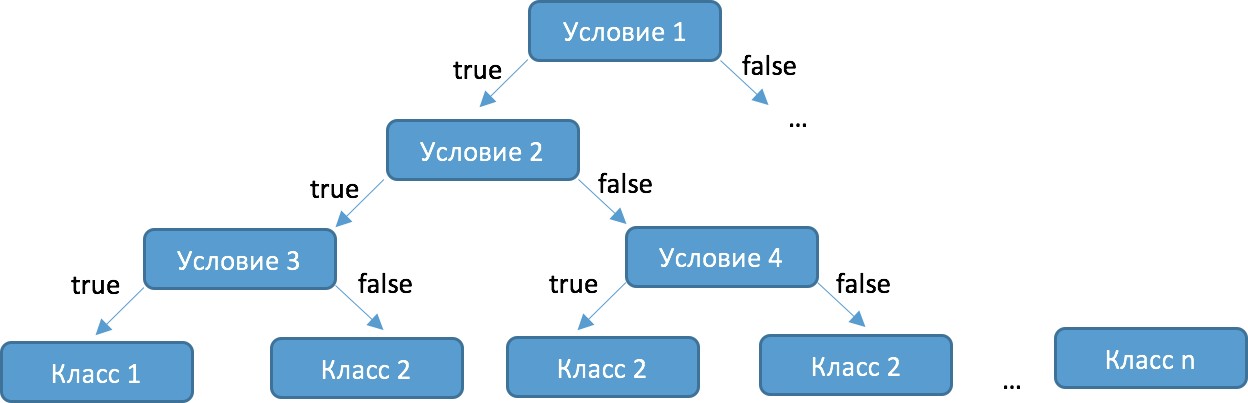 Деревья принятия решений представляют собой логические схемы, которые позволяют получить конечный результат классификации объекта с помощью набора ответов на иерархически организованную систему вопросов. Структура дерева решений содержит 2 класса объектов: листья и ветви. Листья дерева решений содержат в себе условия для значений переменных, описывающих отдельный объект классификации. Листья дерева решений могут быть внутренними и терминальными. Внутренние вершины содержат предикаты, позволяющие направить объект классификации по соответствующей ветви. Терминальные вершины содержат в себе конечную метку класса. Пример решающего дерева представлен на риc. 3.7.Риc. 3.7. Структура решающего дерева Информационная энтропия представляет собой меру неопределённости некоторой системы (в статистической физике или теории информации), в частности непредсказуемости появления какого–либо символа алфавита. В последнем случае уровень энтропии численно равен количеству информации на символ передаваемого сообщения. Функция энтропии Шеннона имеет вид:  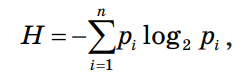 Где: pi – это вероятность нахождения системы в i–ом состоянии. Следует отметить, что чем выше уровень энтропии H, тем ниже уровень упорядоченности в системе. Таким образом, перед аналитическими алгоритмами ставится задача минимизации функции энтропии. При прогнозировании качественного признака (задача классификации) алгоритм построения дерева решений включает в себя следующие шаги: – расчёт уровня энтропии исходной выборки; – перебор возможных условий первого листа дерева решений (для каждого элемента выборки необходимо перебрать все его атрибуты и сгенерировать предикат, способный разделить выборку); – расчёт нового уровня энтропии системы при разделении выборки на основании каждого предиката; – выбор предиката, при котором будет наблюдаться максимальное снижение уровня энтропии; – повторение предыдущих шагов рекурсивно до тех пор, пока в каждой из–под выборок не окажутся объекты одного класса. В случае прогнозирования количественного признака (задачи регрессии) используется другая метрика оценки прироста упорядоченности при разбиении выборки, так называемая дисперсия вокруг среднего: 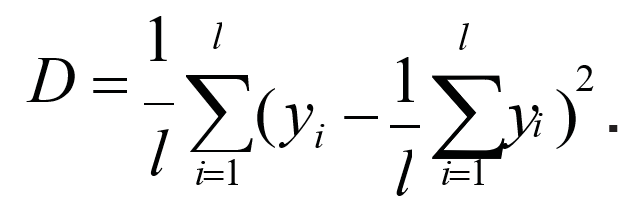 Таким образом, алгоритм построения дерева решений при решении задачи регрессии будет выполняться до того момента, пока в каждой из–под выборок не окажутся объекты со значением целевой переменной в допустимом диапазоне. Пример расчёта уровня энтропии системы и построения дерева решений Построим дерево решений (рис. 3.8). 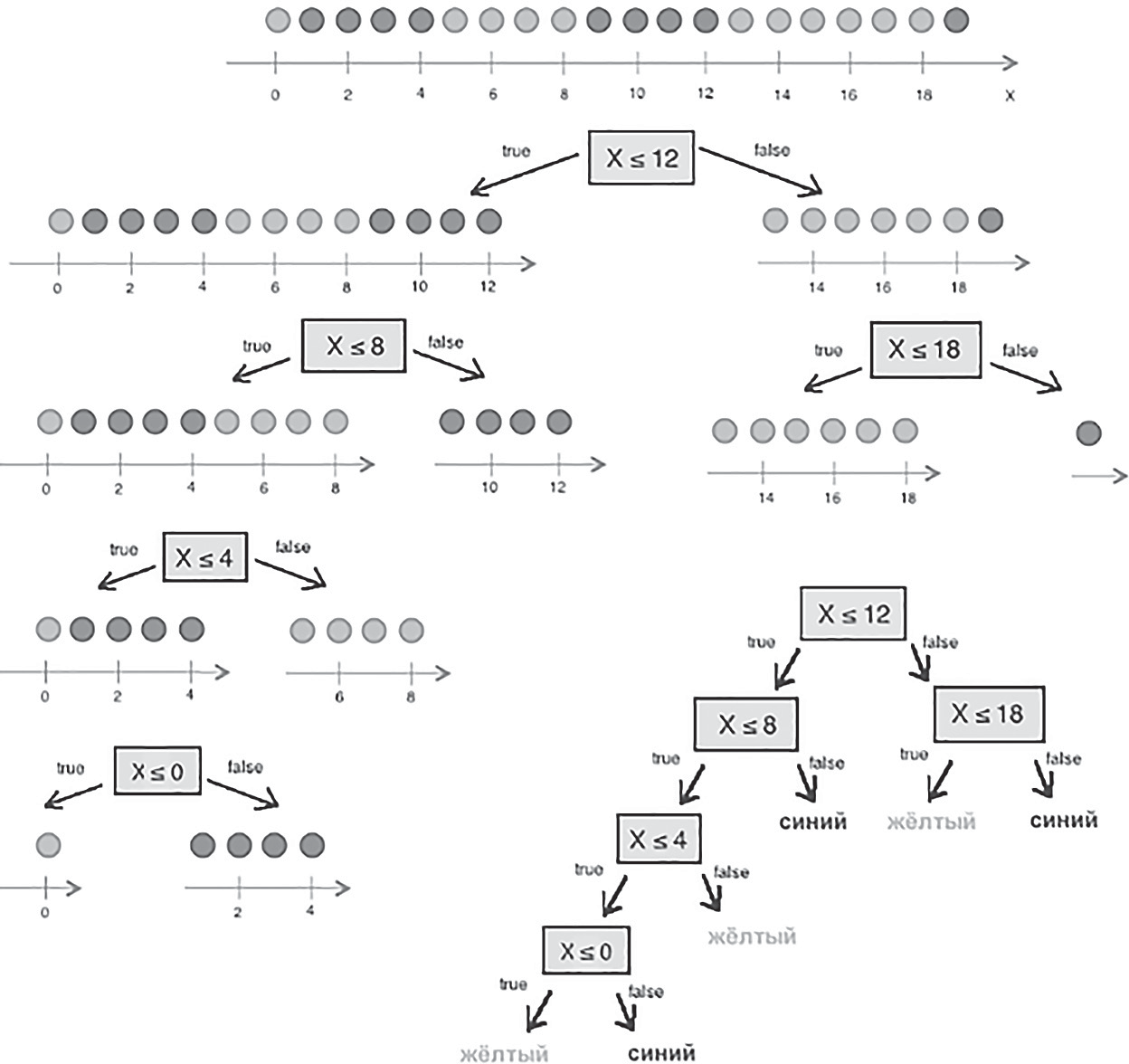 Риc. 3.8. Дерево решений KNN (Метод k ближайших соседей) Метод k ближайших соседей – это алгоритм, который применяется в решении задач классификации и регрессии. KNN основывается на гипотезе компактности. Гипотеза компактности – это предположение о том, что схожие объекты гораздо чаще лежат в одном классе, чем в разных; или, другими словами, что классы образуют компактно локализованные подмножества в пространстве объектов. Из вышесказанного также можно сделать вывод, что граница между классами имеет достаточно простую форму. Пусть задана обучающая выборка пар «объект–ответ» 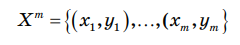 Пусть на множестве объектов задана функция расстояния p (x, xm). Задачей этой функции является отображение степени сходства/различия между объектами выборки. Таким образом, значение функции расстояния между объектами обратно пропорционально степени схожести объектов выборки. Первым этапом реализации метода ближайших соседей является выбор адекватной задаче метрики расстояния и расчёт расстояний между объектами выборки. Для расчёта меры расстояния между объектами выборки используют следующие метрики: евклидово расстояние, квадрат евклидова расстояния, манхэттенское расстояние, степенное расстояние и др. Евклидово расстояние d (p, q) для точек p = (p1, …, pn) и q = (q1, …, qn) рассчитывается по формуле: 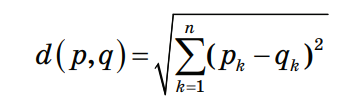 Квадрат евклидова расстояния: 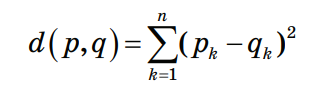 Манхэттенское расстояние: 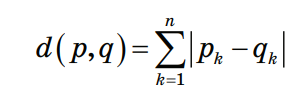 Степенное расстояние: 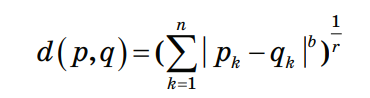 Где: b и r это параметры настройки модели, определяемые пользователем. После выбора метрики и расчёта расстояний необходимо отсортировать объекты выборки по возрастанию значения функции расстояния p (x, xm) до классифицируемого объекта. Таким образом, алгоритм классификации KNN включает в себя следующие шаги: – нормализация данных; – вычисление расстояний между объектами выборки; – сортировка объектов выборки по убыванию значения функции расстояния p (x, xm); – присвоение анализируемому объекту класс, наиболее часто встречающийся среди k соседей. Одним из механизмов настройки работы алгоритма классификации KNN является перебор параметра k (количество k соседей). При k = 1 алгоритм ближайшего соседа является неустойчивым к шумовым выбросам. При k = m, степень устойчивости предельно растет и результат работы алгоритма превращается в константу. Учитывая вышеперечисленное, можно сделать вывод о том, что оптимальное значение параметра k отличается от крайних значений k = 1 и k = m, где m количество элементов выборки. Для подбора оптимального параметра k используют алгоритм кросс–валидации. Кросс–валидация – это группа методов оценки качества предиктивной модели, которые основываются на перекрестном разбиении первичной выборки на обучающие и тестовые наборы данных и получении усредненного результата по всем случаям разбиения. Схема перекрестного разбиения набора данных представлена на рисунке 3.9. 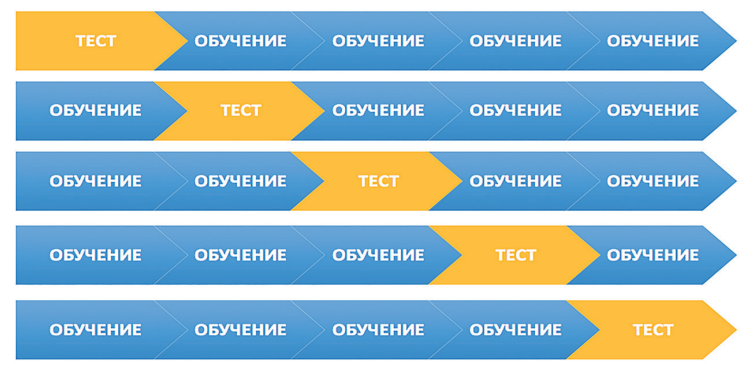 Рис 3.9. Схема кросс–валидации Кросс–валидация позволяет осуществлять более взвешенный выбор архитектуры модели анализа данных, однако является ресурсоемкой операцией, сложность которой резко возрастает с увеличением объема, анализируемых данных. Нормализация данных является необходимым этапом подготовки данных в тех случаях, когда поля различных признаков содержат данные в разных единицах измерения. Если не производить нормализацию данных, признаки, значения которых находятся в диапазоне от 0 до 100, окажут большее влияние на целевую переменную, чем признаки, значения которых находятся в диапазоне от 0 до 10. Нормализация величины xj производится по формуле: 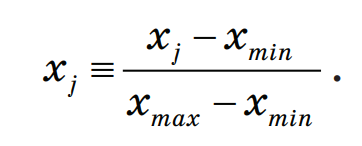 Результатом нормализации является набор данных, значения признаков которого варьируются в диапазоне от 0 до 1 и таким образом содержит относительные величины вместо абсолютных. Вышеописанная операция позволяет нивелировать влияние признаков. Пример нормализации данных и классификации нового наблюдения методом k ближайших соседей. В таблице представлен классифицированный (размеченный) набор данных о наблюдениях, собранных по двум признакам, значения которых варьируются от 0 до 1000 для первого признака и от 0 до 10 для второго. Проведем классификацию Наблюдения 19 со значениями признаков: Признак 1 – 90 Признак 2 – 1,3
Шаг 1. Нормализация данных Произведем нормализацию набора данных, после чего значения признаков будут варьироваться в диапазоне от 0 до 1 и таким образом содержать относительные величины вместо абсолютных. Нормализация значений признаков наблюдения 1: Нормализация признака 1: 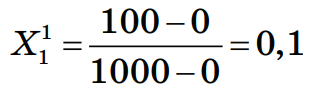 Нормализация признака 2: 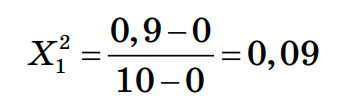 Нормализованные значения признаков запишем в таблицу:
Шаг 2. Нормализация значений признаков нового наблюдения Произведем нормализацию значений признаков нового наблюдения согласно их диапазонам. Нормализация значений признаков наблюдения 19: Нормализация признака 1: 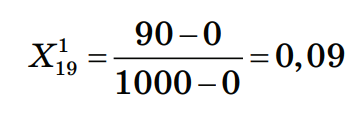 Нормализация признака 2: 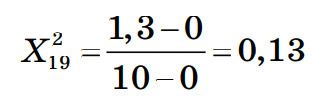 Шаг 3. Сортировка объектов выборки по убыванию значения функции расстояния Ниже приведён расчёт расстояния между Наблюдением 1 и Наблюдением 19: 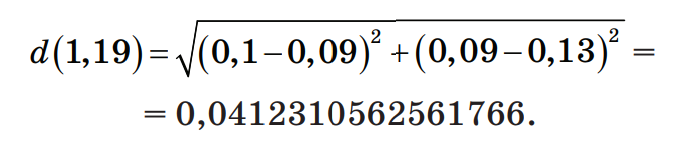 Рассчитаем расстояния до других наблюдений и запишем их в таблицу, округлив до 4–х знаков после запятой, а затем отсортируем получившийся массив по возрастанию расстояния до классифицируемого наблюдения:
Шаг 4. Определение числа k соседей На этом шаге необходимо выбрать число соседей и определить, к какому классу принадлежит большинство из них. Если k = 1, то ближайшим соседом будет Наблюдение 10 и результатом классификации будет Класс 2. Если k = 2, то Наблюдение 19 будет классифицировано в Класс 2 и Класс 1 с равной долей вероятности. При k = 4 результатом классификации является Класс 2. Таким образом, очевидно, что результат классификации сильно зависит от значения параметра k. При выборе слишком малого значения k присутствует риск того, что ближайшими соседями классифицируемого наблюдения окажутся выбросы. В таком случае результат классификации окажется неверным. Существует возможность минимизировать подобный риск ограниченным увеличением числа соседей. В случае, когда выбрано максимальное количество соседей k = N, где N это общее количество наблюдений выборки, классифицируемому объекту будет присваиваться наиболее часто встречающийся класс, результат алгоритма превратится в константу для данной выборки. Обычно значение параметра k может варьироваться от 3 до 10 и часто оказывается близким к квадратному корню от числа всех наблюдений выборки. Оптимизация числа соседей достигается перебором значений параметра k на тестовых выборках при кросс–валидации. Метрики качества Для сравнения эффективности применения различных алгоритмов машинного обучения существует необходимость определения метрики качества, которые могут выступить в качестве индекса производительности P для задач класса T. Классическими метриками качества для задач регрессии являются средняя абсолютная (Mean Absolute Error, MAE) и средняя квадратичная ошибки (Mean Squared Error, MSE). 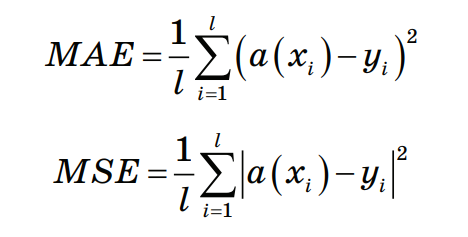 Описание метрик качества для задач классификации требует представления следующей концепции для описания этих метрик в терминах ошибок классификации, которые в англоязычной литературе именуются как confusion matrix (матрица неточностей). Рассмотрим пример: допустим, что у нас есть два класса и алгоритм, предсказывающий принадлежность каждого объекта одному из классов, тогда матрица ошибок классификации будет выглядеть следующим образом:
Здесь ŷ – это ответ алгоритма для данного объекта, а y – истинная метка класса на этом объекте; TP – True Positive – доля правильных прогнозов «попадание»; TN – True Negative – доля случаев, при которых модель разумно проигнорировала объекты выборки; FP – False Positive – доля ложных прогнозов «лож– ная тревога»; FN – False Negative – доля случаев, при которых модель проигнорировала объекты, действительно относя– щиеся к искомому классу «пропуск цели». Точность (Preceision): 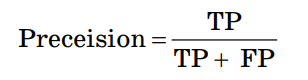 Точностью работы алгоритма в данном случае является доля правильно классифицированных объектов выборки от общего числа случаев классификации. Полнота (Recall): 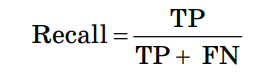 Полнотой работы алгоритма является доля правильно классифицированных объектов выборки от общего числа объектов, действительно находящихся в целевом классе. F–мера (F–measure): 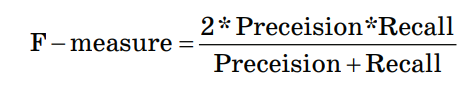 F–мера является гармоническим средним показателей точности и полноты. Accuracy: 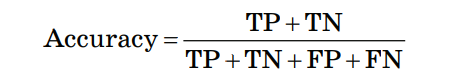 Мера Accuracy представляет собой консолидированный показатель точности работы модели по всем классам. Пример расчета качества работы алгоритма классификации Пусть из 10100 единиц эксплуатируемого оборудования откажет 100 единиц и есть алгоритм, правильно предсказывающий 90 отказов. Построим матрицу неточностей:
Точность (Preceision) Preceision = 90 = 0,9 90 + 30 Полнота (Recall) Recall = 90 = 0,9 90 + 30 F–мера (F–measure) F – measure = 2*0,9*0,9 = 0,9 0,9 + 0,9 Accuracy Accuracy = 90+9950 = 0,95 90 + 9950 + 30 + 30 |