Ответы на Вопросы моделирование. Дайте определение основным понятиям и терминам моделирования хим тех процессов. (модель хтп, хтс, моделирование, классификации моделей, традукция мат модели )

• Название: Дайте определение основным понятиям и терминам моделирования хим тех процессов. (модель хтп, хтс, моделирование, классификации моделей, традукция мат модели )
• Дата: 26.04.2023
• Размер: 1.49 Mb.
• Имя файла: Ответы на Вопросы моделирование.docx
• Тип: Документы; #1091330
• страница: 3 из 4

Основы математического моделирования элементов ХТС на примере модуля смесителя. (Схема, матер. и тепловой балансы, допущения при моделировании)

В соответствии с исходной задачей, два потока вещества, имеющие расходы G₁ и G₂(моль/сек), температуры T₁ и T₂ (град.К), составы X_1i и X_2i (мольные доли), теплоту Q₁ и Q₂(Вт) подаются в смеситель, откуда выходит один поток с расходом G₃, температурой T₃, составом Х_3i и теплотой Q₃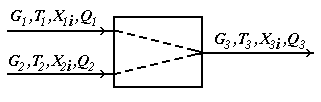



Обычно при составлении упрощенной детерминированной модели принимаются некоторые допущения. Для смесителя, допущения будут следующие:

1. 
   Структура потока в аппарате соответствует режиму идеального смешения; В противном случае, поток на выходе смесителя будет не полностью перемешанный, и, в таком случае необходимо будет либо усложнять модель с учетом коэффициента перемешивания, либо усложнять модель с учетом гидродинамики потоков в аппарате. Это может быть не оправдано по удельным затратам времени на разработку модели, а при неполном учете в модели всех протекающих физико-химических явлений приводить к значительным ошибкам.
   
2. 
   Процесс смешения – адиабатический, не учитывается теплота смешения; В противном случае необходимо учитывать процессы подвода и отвода теплоты, а также теплоту смешения, выделяющуюся при смешении веществ (в особых случаях, в тепловом балансе смесителя требуется учитывать теплоту смешения).
   
3. 
   Все потоки имеют одно фазовое состояние; В противном случае модель нужно будет значительно усложнить, т.к. необходимо использовать смеситель, имеющий 2 или 3 выходных потока (газ, жидкость и твердое), т.к. одним потоком невозможно одновременно выразить различные фазовые состояния, будет необходимо учитывать фазовое равновесие в системе твердое-жидкость-газ, и условия его установления, а также тепловой баланс процессов установления фазового равновесия.
   
4. 
   Давление входных и выходных потоков – одинаковое; При изменении давления могут возникнуть условия, приводящие к изменению фазового состояния
   

Общее уравнение материального баланса запишется: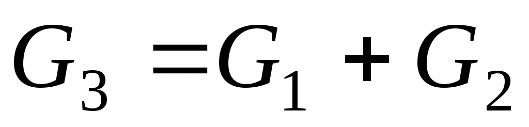



С использованием уравнения материального баланса для вещества можно рассчитать состав выходного потока: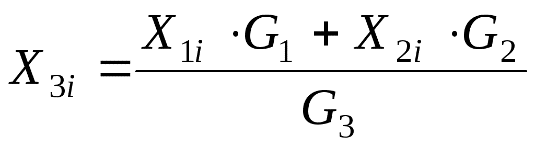



Общее уравнение теплового баланса запишется:



Температура выходного потока рассчитывается методом итераций: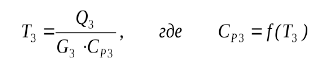

10. 
    Основы математического моделирования элементов ХТС на примере модуля делителя. (Схема, матер. и тепловой балансы, допущения при моделировании)
    

Модуль делителя является одним из наиболее простых модулей. В соответствии с исходной задачей, поток вещества, имеющий расход G₁ (моль/сек), температуру T₁ (град.К), составы X_1i (мольные доли) и теплоту Q₁ (Вт) подается в делитель, откуда выходят два потока с расходами G₂ иG₃, температурами T₂ и T₃, составами X_2i и Х_3i и теплотой Q₂ и Q₃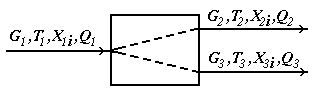



Для делителя, допущения будут следующие:

1. 
   Состав, температура и давление выходных потоков равны составу, температуре и давлению входного потока;
   
2. 
   Все потоки имеют одно фазовое состояние.
   

Известно два способа деления потока. Для ПЕРВОГО способа требуется знать расход первого выходящего потока, а для ВТОРОГО – коэффициент деления потока. В зависимости от типа связанного с делителем оборудования, применяться могут оба способа, однако ПЕРВЫЙ способ имеет ограничения, которые заключаются в том, что используются абсолютные значения, а не относительные. Например, в процессе расчетов, расход входящего потока будет меньше заданного расхода первого выходящего потока, т.е. второй выходящий поток будет иметь отрицательный расход, что невозможно. ВТОРОЙ способ более стабильный в расчетах, т.к. используются относительные значения, однако, в зависимости от типа связанного с делителем оборудования, использование фиксированного коэффициента деления может не соответствовать реальной ХТС.

Для реализации ПЕРВОГО способа необходимо знать: расход G₁ (моль/сек), температура T₁ (град.К), состав X_1i (мольные доли) и теплота Q₁ (Вт), также расход первого выходящего потока G₂.

Основное уравнение материального баланса запишется:



Исходя из допущения, состав выходных потоков будет равен составу входного потока:

10. 
    Основы математического моделирования элементов ХТС на примере модуля теплообменника. (Схема, виды теплообменников, матер. и тепловой балансы, основные формулы при расчете параметров теплообменника – алгоритм решения)
    

В отличие от модулей смесителя и делителя, модуль теплообменника не является столь простым, т.к. при изменении температуры потоков возможно изменение их фазового состояния, а, следовательно, при расчете необходимо учитывать такие изменения. В связи с этим, например, только для систем газ-газ, жидкость-жидкость и газ-жидкость различают следующие модели теплообменников:

1. 
   Теплообменник газ-газ или жидкость-жидкость без фазовых переходов (нагреватели и холодильники);
   
2. 
   Теплообменник газ-газ или жидкость-жидкость с фазовым переходом (для системы газ-газ он называется конденсатор, а для системы жидкость-жидкость – испаритель, также существует более сложный вариант, когда тепло от конденсирующегося газа используется для испарения жидкости);
   

Кроме того, так как на процесс расчета теплообменника оказывает влияние его конструкция, то для каждого указанного выше типа теплообменников различают следующие модели:

1. 
   Противоточный ("холодный" и "горячий" агенты идут навстречу друг другу, т.е. противотоком);
   
2. 
   Прямоточный ("холодный" и "горячий" агенты идут параллельно, т.е. прямотоком);
   
3. 
   Перекрестноточный (промежуточный вариант между указанными выше);
   
4. 
   Одноходовой или многоходовой теплообменники (в многоходовых теплообменниках часть труб работает в режиме противотока, а часть – в режиме прямотока, или в многоходовом перекрестноточном теплообменнике жидкость или газ по трубам может двигаться по ходу или против хода потока в межтрубном пространстве);
   
5. 
   Варианты, когда один из агентов (или оба агента) движется за счет естественной конвекции, которые, по интенсивности перемешивания потока за счет естественной конвекции, в свою очередь делятся на горизонтальные и вертикальные;
   
6. 
   Теплообменники смешения ("холодный" и "горячий" агенты непосредственно контактируют друг с другом, например, в аппарате с насадкой).
   

И, наконец, теплообменники, различающиеся по режиму работы на:

1. 
   периодические;
   
2. 
   непрерывные.
   

В качестве примера рассмотрим проверочный расчет теплообменника-подогревателя для системы газ-газ, жидкость-жидкость или газ-жидкость с учетом следующих допущений:

• 
  Одноходовой кожухотрубный теплообменник в стационарном режиме;
  
• 
  Теплопередача не сопровождается изменением агрегатного состояния;
  
• 
  Коэффициенты теплоотдачи для "холодного" и "горячего" потоков рассчитывается при начальных температурах теплоносителей;
  
• 
  Схема движения потоков – противоточная;
  
• 
  Потери теплоты отсутствуют.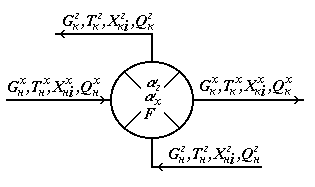
  

10. 
    Методы поиска оптимума целевой функции. (назвать и рассказать какие основные методы существуют, подробнее остановиться на численных методах: оптимизация перебором, сканирование, метод золотого сечения).
    

Метод множителей Лагранжа  Здесь вместо решения системы конечных уравнений для отыскания оптимума необходимо интегрировать систему диф-ференциальных уравнений. Множители Лагранжа используют так же в качестве вспомога-тельного средства при решении задач с ограничением типа равенств в вариационном исчи-слении и динамическом программировании. Следует особо подчеркнуть, что метод множи-теля Лагранжа позволяют найти лишь необходимые условия существования условного экс-тремума для непрерывных функций, имеющих к тому же непрерывные производные.

Полученные в результате решения значения неизвестных X_i должны быть проверены на экстремум с помощью анализа производных более высокого порядка или другими методами.

Методы вариационного исчисления Оптимальные задачи, когда решение представляется не как совокупность значения конечного числа переменных, а как совокупность функции, вид которых заранее не известен, составляют сущность вариационного исчисления. Вариационное исчисление применяется для оптимизации математически описанных процессов.

При статистической оптимизации процессов с распределенными параметрами или в задах динамических оптимизации. Вариационные методы позволяют в этом случае свести решение оптимальной задачи к интегрированию системы дифференциальных уравнений Эйлера.

Методы детерминированного и случайного поиска. их можно классифицировать на методы и пассивного и направлен-ного поиска. Последние, в свою очередь, делятся на одноэтапные (градиентные, случайного поиска) и многоэтапные (метод поочерёдного изменения переменных). В основу градиентных методов поиска положены вычисление и анализ произ-водных целевой функции R(х). Если зависимость R(х) нельзя записать в явном или анали-тическом виде, то единственным способом определения производных R(х) является приме-нение численного метода.

Метод релаксации заключаются в отыскании осевого направления, вдоль которого функция цели изменяется наиболее быстро. Осевому направлению соответствует наибольшая по модулю производная. В случае минимизации движение совпадает с направлением оси (знак производной отрицательный) и шаги делаются до тех пор, пока не будет получено минимальное значение по выбранному осевому направлению. После чего вновь определя-ются производные по всем переменным за исключением той, по которой осуществляется

спуск, и снова выбирается осевое направление скорейшего убывания функции цели, по которому производятся дальнейшие шаги. Критерием окончания поиска оптимума является достижение такой точки, из которой по любому осевому направлению дальнейшего убывания функции цели не происходит (рис.4.5). Хотя метод релаксации обладает определенными достоинствами перед методом градиента, поскольку при спуске вдоль выбранного осевого направления не требуется вычисления производных, однако движение происходит все же не в оптимальном направлении, т.к. градиент в данном случае не совпадает с осевым направле-нием.

В методе наискорейшего спуска нашло сочетание основных идей и методов релак-сации и градиента. Суть метода заключается в том, что после определения в начальной точке градиента оптимизируемой функцией направление движения поиска сохраняется неизмен-ным до тех пор, пока в этом направлении не будет найден минимум. После чего вычисляется градиент и определяется новое направление поиска. Данный метод является более выгодным из-за сокращения объема вычисления, особенно вдали от оптимума. Вблизи оптимума на-

правление градиента меняется резко, поэтому указанный метод автоматически переходит в метод градиента. Важной особенностью наискорейшего спуска (рис.4.6) является то, что при его применении каждое новое направление движения к оптимуму ортогонально предшест-вующему.

Метод "тяжелого шарика" в отличие от ранее рассмотренных может быть исполь-зован в задачах с целевыми функциями, имеющими несколько локальных экстремумов и характеризуется в этом смысле как метод поиска глобального экстремума.

К недостаткам градиентных методов следует отнести то, что для определения

направления движения требуется вычислить значение производной от функции по каждому параметру.

Вычисление производных может быть неточным из-за разнородности параметров, по которым выполняется оптимизация. Поэтому все параметры приводят к безразмерному виду. Поверхность отклика может оказаться такой, что придется часто изменять направление движения, а это приводит к значительным затратам времени при обращении к математиче-ской модели

Безградиентные методы детерминированного поиска используют процесс

поиска информации, получаемую не при анализе производных, а от сравнения величины критерия оптимальности в результате выполнения очередного шага.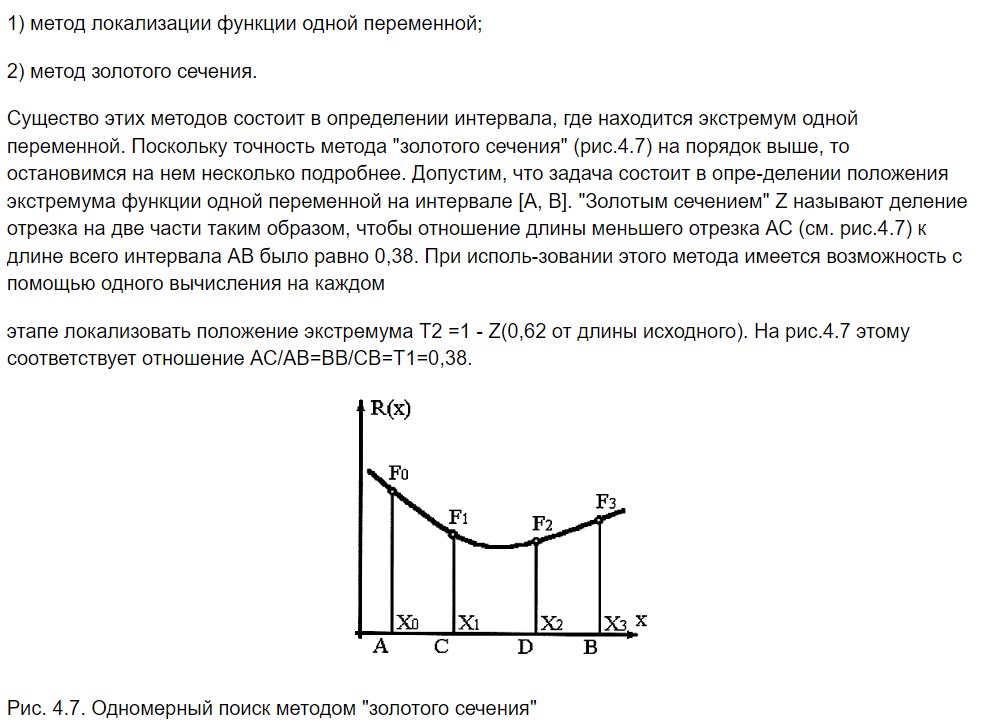



Метод поочерёдного изменения переменных, называемый также методом Гаусса- Зейделя, относится к методам многоэтапного направленного поиска и по существу аналогичен методу релаксации. Отличие в том, что не определяется новое направление с помощью производных, а поочередно изменяются независимые переменные, чтобы по каждой из них достигалось экстремальное значение целевой функции. Стратегия поиска минимума по каждой перемен-ной может быть любая, целесообразно использовать здесь и методы поиска экстремума

функции одной переменной. Простота и сравнительно небольшой объём вычислений, необ-ходимых для его реализации, обусловили его распространение в системах автоматического поиска оптимума функции цели

10. 
    Структурный и эмпирический подходы к описанию ХТС. (в чем заключаются оба подхода, различии, в каких случаях применяются, привести примеры)
    

Существует два подхода к описанию системы. Первый подход можно назвать структурным. Суть его заключается в следующем. Для создания математической модели системы прежде всего исследуем ее структуру – составляющие систему элементы и характер их взаимодействия. Применительно к технологическому процессу это означает расшифровку его механизма. В результате получается схема процесса – его мысленная модель. Для химико-технологического процесса мысленная модель на физическом языке содержит прежде всего представления о механизмах реакций, характере движения потоков, процессах переноса тепла и вещества и о взаимном влиянии химизма, гидравлики, тепло- и массопереноса. Записав эту схему на языке математики, получаем некую систему уравнений, описывающих процесс. Обычно на этом этапе уравнения получаются в общем виде – в них входят некоторые пока неизвестные коэффициенты (константы скоростей реакций, коэффициенты тепло- и массоотдачи и др.). Эти коэффициенты называют параметрами модели. Для определения параметров ставится эксперимент (на моделях, а иногда и на оригинале, если таковой имеется), результаты которого позволяют получить математическое описание в полном виде, со всеми коэффициентами. Второй подход к описанию системы – эмпирический. Другое его распространенное название – метод черного ящика. Предположим, что структура интересующей нас системы скрыта от нас (как бы заключена в «черный ящик»). Это не означает, что системой нельзя управлять. Как бы черен ни был ящик, у системы есть важные контакты, которыми можно воспользоваться для ее анализа и управления ею. Эти контакты – входы и выходы системы. Будем изменять значения входов и определять, как при этом изменяется отклик. Каждый такой акт – изменение входов и определение отклика – есть не что иное, как эксперимент. Проведя определенное число экспериментов, опишем их результаты эмпирическим уравнением или системой эмпирических уравнений. Эти уравнения и будут математической моделью, которой можно воспользоваться для моделирования данной системы.

Любое эмпирическое описание отражает, хотя и в неявной форме, механизм процесса. Иногда это отражение оказывается настолько характерным и точным, что анализ эмпирического уравнения прямо приводит к раскрытию механизма. Эмпирическое уравнение обязательно содержит в себе структуру, но только структуру нерасшифрованную. Поэтому четкое противопоставление обоих подходов носит характер методический, а не прикладной. В практических задачах наблюдаются самые разнообразные соотношения между уровнями структурности и эмпиричности применяемых методов. Главное достоинство эмпирического подхода – простота. Особенно существенно оно сказывается при изучении очень сложных процессов. Главная его слабость – малая надежность экстраполяции. В пределах изменения переменных, изученных в опытах, предсказание поведения процесса (интерполяция) обычно может проводиться достаточно точно. Но закон изменения функций отклика за изученными пределами нам неизвестен и можно допустить серьезную ошибку, полагая, что процесс по-прежнему обязательно будет подчиняться выведенным эмпирическим уравнениям.

В практике моделирования одним из важнейших случаев экстраполяции является масштабирование: предсказание того, как изменятся параметры процесса при переходе от малой модели к большому оригиналу. На основе эмпирических зависимостей эта задача, как правило, решается гораздо хуже, чем при структурном подходе. Главное достоинство данных, полученных на основе структурного подхода, – их большая прогностическая мощность. Зная достаточно полно механизм какого-либо процесса, можно с большой степенью достоверности предсказывать ее поведение в самых разнообразных условиях. Поэтому, как гласит известный афоризм, «нет ничего практичнее хорошей теории». Слабое место подхода – трудность создания хорошей теории сложных процессов. Если выделить лишь один элемент химико-технологического процесса – его гидродинамику, то приходится считаться с отсутствием на сегодня сколько-нибудь удовлетворительной общей теории турбулентности. Далее, современная химия охватывает сотни тысяч веществ, и если задаться целью всерьез расшифровать механизмы реакций получения всех этих веществ, то вряд ли удастся достичь этой цели в обозримый срок. Подобные затруднения встречаются на каждом шагу. Понятно, что рассчитать эмпирические уравнения, как правило, бывает проще, чем получить информацию, достаточную для расшифровки механизма процесса.