Ответы на Вопросы моделирование. Дайте определение основным понятиям и терминам моделирования хим тех процессов. (модель хтп, хтс, моделирование, классификации моделей, традукция мат модели )

Название	Дайте определение основным понятиям и терминам моделирования хим тех процессов. (модель хтп, хтс, моделирование, классификации моделей, традукция мат модели )
Дата	26.04.2023
Размер	1.49 Mb.
Формат файла
Имя файла	Ответы на Вопросы моделирование.docx
Тип	Документы #1091330
страница	2 из 4

1 2 3 4

План эксперимента устанавливает численные значения факторов и условия проведения опытов.

Критерии оптимальности планов и способы организации активного эксперимента можно разделить на три группы.

К I-й группе относят критерии, связанные с точностью оценок коэффициентов регрессии.

Ортогональность позволяет оценивать все коэффициенты регрессии независимо друг от друга и упрощать или усложнять модели, исключая или добавляя новые коэффициенты без пересчета уже найденных. Ортогональность плана эксперимента обеспечивает минимальное число вычислений.

Д-оптимальность обеспечивает минимум обобщенной дисперсии всех оценок коэффициентов. При составлении планов, обеспечивающих минимум обобщенной дисперсии только части оценок коэффициентов, план называется усеченным Д-оптимальным.

А-оптимальность обеспечивает минимум средней дисперсии оценок коэффициентов.

Е-оптимальность не дает возможности некоторым оценкам коэффициентов иметь слишком большие дисперсии.

Ко II-ой группе относят критерии, которые определяют точность предсказания отклика с помощью построенной модели.

Ротатабельность планов обеспечивает одинаковую точность предсказания для точек, равно удаленных от центра плана по любому направлению.

G-оптимальные планы гарантируют отсутствие в области эксперимента точек, имеющих слишком низкую точность оценки отклика.

Q-оптимальные планы минимизируют среднюю дисперсию предсказания.

К III-ей группе относят критерии, связанные со стратегией эксперимента.

Насыщенность плана обеспечивает минимум числа опытов. Минимум задается числом коэффициентов модели. Приближение к нему служит мерой насыщенности плана.

Основные требования, предъявляемые к процессу моделирования. Теория подобия объекта и модели.

1. Модель должна строиться исходя из цели исследования системы (явления, процесса) и соответствия цели точности результатов моделирования.

2. Соответствие целям исследования для решения конкретного класса задач, исходя из которых выбираются существенные свойства системы.

Попытки создания универсальной модели, нацеленной на решение большого числа разнообразных задач, приводят к такому усложнению, что она оказывается практически непригодной. Строить модель, приближающуюся по сложности к реальной системе не имеет смысла.

3. Абстрагирования от второстепенных деталей - упрощение при сохранении существенных свойств системы. Детализация модели определяется необходимой точностью решения задачи для достижения цели исследования.

Модель должна быть в некоторых отношениях проще прототипа и соответствовать реальной системе по уровню сложности исходя из выбранного множества свойств - игнорируются менее существенные свойства, не оказывающие влияния на решение поставленной задачи, детально рассматриваются основные исследуемые свойства.

4. Блочная структура модели и минимальные связи между блоками с учетом разделения модели по этапам и режимам функционирования системы.

Это дает возможность использования накопленного опыта в процессе отработки модели и многовариантной реализации блоков, отличающихся по точности и сложности, - построения ансамбля моделей.

Подобными явлениями называются такие физические явления, которые одинаковы качественно по форме и по содержанию, т.е. имеют одну физическую природу, развиваются под действием одинаковых сил и описываются одинаковыми по форме дифференциальными уравнениями и краевыми условиями.

Обязательным условием подобия физических явлений должно быть геометрическое подобие систем, где эти явления протекают. Два физических явления будут подобны лишь в том случае, если будут подобны все величины, которые характеризуют их.

Для всех подобных систем существуют безразмерные комплексы величин, которые называются критериями или числами подобия.

Основные положения теории подобия формулируют в виде 3-х теорем подобия.

1 теорема: Подобные явления имеют одинаковые числа подобия.

2 теорема: Любая зависимость между переменными, характеризующая какие-либо явления, может быть представлена, в виде зависимости между числами подобия, составленными из этих переменных. Эта зависимость называется критериальным уравнением.

3 теорема: Подобны те явления, условия однозначности которых подобны, и числа подобия, составленные из условий однозначности, численно равны.

Числа подобия, составленные из величин, входящих в условия однозначности называются определяющими. Числа подобия, в которые входят искомые величины, называются определяемыми.

Метод наименьших квадратов. (где используется в мат. моделировании, как с помощью этого метода найти параметры модели, )

Сущность метода наименьших квадратов заключается в отыскании параметров модели тренда, которая лучше всего описывает тенденцию развития какого-либо случайного явления во времени или в пространстве Задача метода наименьших квадратов (сокращенно – МНК) сводится к нахождению не просто какой-то модели тренда, а к нахождению лучшей или оптимальной модели. В свою очередь, модель будет оптимальной, если сумма квадратических отклонений между наблюдаемыми фактическими величинами и соответствующими им расчетными величинами тренда будет минимальной (наименьшей).

Задача определения параметров уравнения регрессии сводится практически к определению минимума функции многих переменных. Процедура метода наименьших квадратов позволяет с высокой точностью определить значения коэффициентов линейного уравнения.

С помощью метода наименьших квадратов можно обрабатывать любые экспериментальные данные, однако, надо отметить, что оптимальность данного метода доказывается только для нормального распределения.

К достоинствам методов МНК и можно отнести следующее: позволяют получать коэффициенты приближенной регрессии, позволяют работать с нелинейными моделями, минимизируют ошибку. Наряду с этим надо отметить и недостатки, а именно: не все модели могут быть приведены к линейному виду, методы дают большую погрешность, когда функция отклика существенно изменяется в выбранном интервале.

Проверка адекватности эмпирической модели.

Адекватность полученного математического описания (уравнения регрессии)– соответствие модели (отклонение данных модели от экспериментальных данных) экспериментальным данным по заданному критерию.

Количественная оценка адекватности может проводиться двумя методами.

Путем определения средней ошибки аппроксимации по формуле:

где N – количество опытных данных, используемых для получения коэффициентов в уравнении регрессии;

Y_м(i) – значение зависимого параметра, рассчитанного по уравнению регрессии;

Y_о(i)- значение зависимого параметра, полученного в эксперименте.

Путем статистической оценки результатов на основе критерия Фишера

Проверка гипотезы адекватности осуществляется путем сравнения дисперсии опытных данных относительно уравнения регрессии S_ост и дисперсии случайной ошибки измерений. Считается, что уравнение регрессии адекватно описывает исследуемый объект, если остаточная дисперсия S_ост исходной величины не превышает погрешности опыта.

Однако, для оценки дисперсии опыта, необходимо иметь несколько значений исходного параметра, полученных при одинаковых условиях.

Если параллельные опыты провести не удается, то проводится оценка качества аппроксимации полученных данных принятому математическому описанию. В этом случае сравнивают дисперсию относительно среднего значения опытных данных S_y и остаточную дисперсию.

Уравнение регрессии имеет смысл, если дисперсия относительного среднего S_y существенно больше, чем остаточная дисперсия S_ост. Для этого исчисляется критерий Фишера F_р, а потом находят его табличное значение F_T(f₁,f₂).

f₁- число степеней свободы числителя - f₁=N-1;

f₂- число степеней свободы знаменателя - f₂=N-n-1;

Степень свободы – число экспериментальных точек, которые можно использовать для оценки дисперсии.

N - количество опытных данных;

n - количество независимых переменных в уравнении регрессии.

Если F_расч< F_крит, то принимается гипотеза об адекватности построенной модели результатам эксперимента.

Если F_расч> F_крит, то линейная модель не является адекватной. В этом случае она дополняется нелинейными членами или переходят к построению планов второго порядка и т.д.

Прямые методы решения систем линейных уравнений. Метод обратной матрицы, метод Гаусса, метод простых итераций.

Итерационные методы решения систем линейных алгебраических уравнений.

Типовые технологические операторы. (4 основных и 3 вспомогательных технологических оператора, изобразить и рассказать про каждый оператор, любой пример)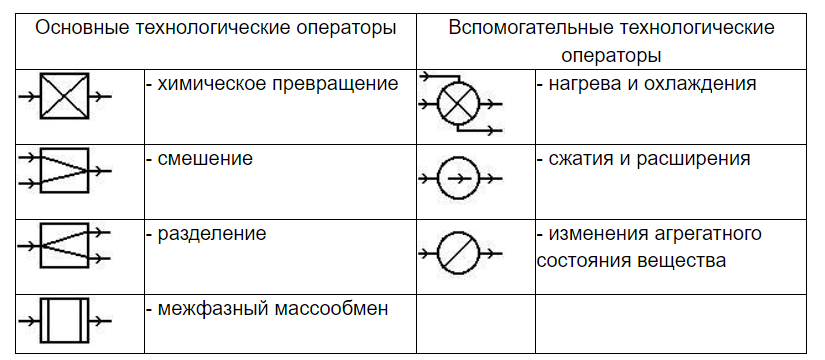

Различия между основными и вспомогательными операторами заключаются в том, что основные технологические операторы обеспечивают функционирование ХТС в требуемом целевом направлении, а вспомогательные – повышают эффективность функционирования системы путем изменения ее энергетического и фазового состояний.

Например, подогреватель, в котором происходит химическая реакция разложения компонентов входного потока, представляет собой совокупность двух типовых технологических операторов – нагрева и химического превращения. Ректификационная колонна непрерывного действия может быть представлена совокупностью двух операторов межфазного массообмена, соответствующих верхней и нижней частям колонны, и оператором смешения. Последний отражает процесс смешения потоков флегмы и исходной смеси на питающей тарелке.

Математическое и физическое моделирование. ( достоинства и недостатки каждого вида моделирования., в каких случаях применяется)

Физическое моделирование - это изучение того или иного явления на нем самом, путем воспроизведения его в уменьшенных масштабах и анализа влияния на него физических особенностей реализации и геометрических размеров. Этот вид моделирования основан на применении принципа подобия объектов и процессов. Подобие объектов характеризуется постоянством отношения основных геометрических размеров.

физическое моделирование сводится к воспроизведению постоянства определяющих критериев геометрического и физического подобия в модели и исследуемом объекте. Этот подход оправдан лишь при изучении сравнительно несложных процессов (гидродинамических или тепловых с одномерным потоком). При исследовании систем, характеризующихся комплексом гидродинамических, тепловых, массообменных и химических процессов (гетерогенная химическая реакция в трубчатом реакторе) физическое моделирование может привести к большому набору критериев подобия, которые часто оказываются несовместимыми (равенство одних исключает равенство других). В настоящее время методы физического моделирования используются для нахождения доверительных интервалов изменения коэффициентов, входящих в уравнения математических моделей (например, констант скорости химических реакций), т.е. для оценки адекватности математических моделей объектам исследования.

Математическое моделирование - это представление закономерностей поведения объекта исследования в виде математических соотношений. Математической моделью называют систему уравнений и неравенств, которые включают наиболее значимые характеристики исследуемого объекта или процесса и упрощенно отражают взаимосвязи между ними. Математическая модель позволяет определить значения выходных и внутренних характеристик объекта или процесса по известным значениям входных характеристик с учетом возмущающих и управляющих воздействий без экспериментальных исследований (в том числе и при отсутствии самого объекта).

Например, для кожухотрубчатого теплообменника входными параметрами могут быть требуемая тепловая нагрузка, виды теплоносителей, их начальные температуры; выходными параметрами - диаметр и длина корпуса, толщина стенки, число труб, конечные температуры теплоносителей; возмущающими воздействиями - наличие застойных зон, “проскока” теплоносителей, загрязнение поверхности теплообмена, управлениями - расходы теплоносителей.

Преимущества математических моделей перед физическими: а) существенно меньшие затраты времени на моделирование; б) не требуют затрат материалов, сырья, энергоресурсов; в) за одинаковое время позволяют провести много большее количество «экспериментов» (пуск, изменения режима работы, останов модельной установки требуют значительных затрат времени); г) пригодны для описания целого класса подобных объектов. Недостаток: учесть и описать математически все явления, присущие объекту, невозможно. Области практического использования математических моделей: - изучение закономерностей протекания природных и производственных процессов (научные исследования); - воспроизведение условий протекания процессов по известным результатам (косвенные измерения, медицинская диагностика); - прогнозирование хода процессов и их результатов (автоматическое управление, метеорология, социология, военное дело); - решение оптимизационных задач (оптимальное управление, оптимальное планирование, оптимальное конструирование).

Понятие системы в химической технологии. Принцип иерархичности и соподчинённости структуры системы. (определение, виды систем, иерархия подсистем, классификация входов системы)

химико-технологическая система (ХТС) - совокупность аппаратов, связанных между собой потоками и функционирующих как единое целое. В каждом аппарате или элементе по терминологии теории систем, происходит преобразование потока (смешение) разделение, измельчение, нагрев, преобразование энергии, сжатие, расширение, химическое превращение, испарение и т.д.). Потоки, или связи no терминологии систем, обеспечивают передачу вещества или энергии между аппаратами (элементами системы) и могут быть материальными, тепловыми, энергетическими. Функционирование ХТС характеризуют состояние ХТС т.е. показателями всех потоков и аппаратов . Показатели потоков называют параметрами которые разделяются на параметры состояния и параметры свойств. К первым относятся расход и концентрация компонентов в потоке, температура, давление и др., ко вторым – теплоемкость, вязкость, плотность. Показателями аппарата (элемента) являются параметры выходящих и входящих потоков, показатели управляющих воздействий, некоторые параметры состояния этого элемента, определяющие его функционирование в данный момент времени и существование для оценки состояния ХТС в целом (активность катализатора, максимальная температура в аппарате и др.).

Обычно различают четыре основных уровня иерархии элементов (подсистем) ХТС:

1. Типовые ХТП и их совокупность в масштабах машин и аппаратов;

2. Агрегаты и комплексы, представляющие совокупность типовых процессов в масштабах производств и их отдельных участков;

3. Совокупность производств в масштабе выпуска товарной продукции;

4. Химическое предприятие в целом.

Иерархическая структура ХТС позволяет на каждом этапе сократить размерность исследуемой задачи (т.е. число одновременно учитываемых элементов и процессов), а результаты изучения подсистемы одного производства использовать в исследованиях другого. Иерархическую структуру масштабных подсистем можно представить также для функциональных подсистем.

По функциональному признаку, наиболее часто используемому технологами, выделяют следующие подсистемы ХТС:

- подсистема подготовки сырья;

- подсистема химического превращения;

- подсистема выделения целевого продукта;

- подсистема обработки технического продукта;

- энергетическая подсистема;

- экологическая подсистема.

Подсистема химического превращения является главной подсистемой ХТС, здесь происходит получение целевого продукта.

Подсистему подготовки сырья вводят в том случае, если сырье по своим характеристикам не соответствует требованиям главной подсистемы. Операторами этой подсистемы являются хранение и транспортировка сырья, нагрев и охлаждение, испарение, плавление, растворение, сушка, измельчение и др.

Подсистема выделения целевого продукта предназначена для разделения реакционной смеси на отдельные компоненты. Операторы подсистемы – ректификация, экстракция, фильтрация и др.

Подсистема обработки технического продукта имеет целью доведение целевого продукта до заданного уровня качества и придания ему товарного вида. В эту подсистему могут быть включены операторы расфасовки, укупорки, маркировки, транспорта, хранения и др.

Энергетическая подсистема включает в себя подсистемы производства энергии, рекуперации энергии и водоподготовки.

Экологическая подсистема предназначена для рекуперации сырья, очистки сточных вод и газовых выбросов.

В состав ХТС кроме элементов включаются еще связи. Связь - это физический канал, по которому происходит обмен веществом, энергией или информацией между элементами (внутренние связи) и между отдельными системами (внешние связи). По физическому смыслу связи бывают материальные, энергетические и информационные.

1 2 3 4