ДИПЛОМ2.doc Окладникова. Дипломнаяработа по специальности 031200 педагогика и методика начального образования
 Скачать 1.4 Mb. Скачать 1.4 Mb.
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Классы | Сравнение | |||
| Низкий уровень | Ниже среднего | Средний уровень | Высокий уровень | |
| Экспериментальный | 4 ученика 20% | 4 ученика 20% | 7 ученика 35% | 5 учеников 25% |
| Контрольный | 2 ученика 10% | 3 ученика 15% | 8 учеников 40% | 7 ученика 35% |
Таблица 2
Выявление уровня владения операцией классификации у младших школьников
| Классы | Классификация | |||
| Низкий уровень | Ниже среднего | Средний уровень | Высокий уровень | |
| Экспериментальный | 4 ученика 20% | 7 ученика 35% | 6 учеников 30% | 3 ученика 15% |
| Контрольный | 3 ученика 15% | 5 учеников 25% | 7 ученика 35% | 5 учеников 25% |
Анализ результатов таблиц позволяет сделать предварительный вывод о слабой сформированности логических операций сравнения и классификации у младших школьников.
Экспериментальный и контрольный классы имеют примерно одинаковый уровень владения операциями сравнения и классификации, причем этот уровень в целом ниже среднего.
Для наглядности представим цифровые данные педагогического эксперимента в графической форме (диаграмма 1,2).
Д
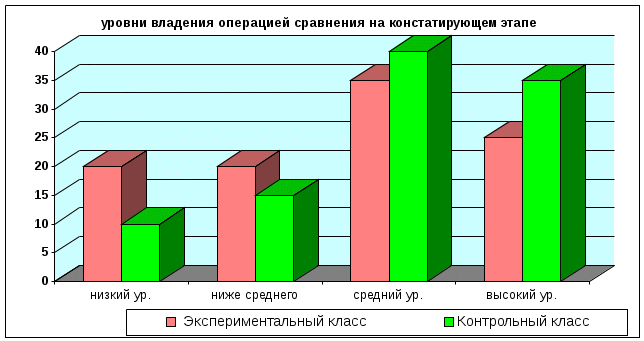
иаграмма 1
Д
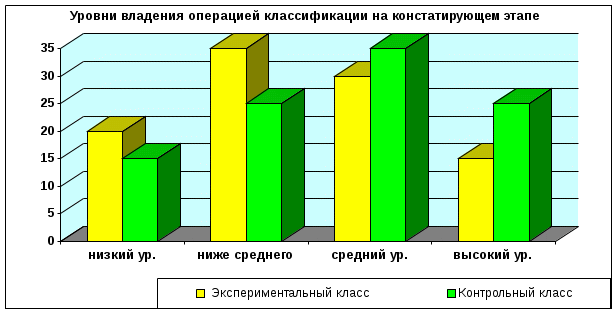
иаграмма 2
Итак, результаты констатирующего этапа эксперимента выявили низкий уровень развития логического мышления у младших школьников, а именно недостаточное владение операциями сравнения и классификации.
3.2. Формирующий этап эксперимента
Для того, чтобы повысить этот показатель, нами был разработан комплекс заданий направленный на развитие операций сравнения и классификации (см. Приложение 4).
Эти задания мы применяли в экспериментальном классе на формирующем этапе эксперимента, который проходил в течение двух месяцев. На формирующем этапе эксперимента участвовали дети 1 «а» класса.
Разработанные нами уроки относились к теме «Числа второго десятка». Данную тему обычно выделяют в отдельный концентр по следующим основаниям.
Здесь учащиеся знакомятся с новой счетной единицей-десятком и с важнейшим понятием десятичной системы счисления - понятием разряда. Усвоение принципов образования, называния и записи двухзначных чисел - основа для усвоения устной и письменной нумерации чисел за пределами сотки.
Изучая арифметические действия над числами второго десятка, учащиеся овладевают основными приемами устных вычислений и одновременно усваивают лежащие в их основе свойства действий, связи между результатами и компонентами, учатся сравнивать и классифицировать. Таким образом, это важная ступень в формировании у детей знаний об арифметических действиях и вычислительных навыков.
Здесь учащиеся начинают усваивать наизусть таблицу сложения и таблицу умножения (запоминают результаты действий над однозначными числами). Прочное усвоение таблиц сложения и умножения - это база для овладения в дальнейшем не только устными и письменными вычислениями с многозначными числами, но и с операциями логического мышления: сравнения и классификации.
В тесной связи с изучением нумерации и арифметических действий формируется понятие о величинах и их измерении, ведется работа над простыми и составными задачами, рассматриваются числовые равенства и неравенства, простейшие уравнения и неравенства с одной переменной. Учащиеся знакомятся с буквой как символом переменной, начинают оперировать буквенными выражениями. Продолжается работа над геометрическим материалом: вводится прямой угол, прямоугольник, обозначение буквами точек, отрезков, углов, многоугольников, рассматривается ломаная, длина ломаной, периметр многоугольника, решаются задачи с геометрическим содержанием. Всё это способствует овладению ими операцией сравнения и классификации.
Задача учителя при изучении этой темы - научить детей считать до 20, показать, как образуются числа из десятков и единиц, научить, читать и записывать двузначные числа на основе твердого знания о том, что единицы пишутся на первом, а десятки - на втором месте, считая справа налево. Необходимо также добиться усвоения учащимися новых понятий и терминов: единицы первого и второго разряда, разрядное число, сумма разрядных слагаемых, однозначное и двухзначное число, сформировать оперативное умение сравнивать и классифицировать.
В изучении нумерации выделяются две ступени: сначала изучается нумерация чисел 11 - 20. При написании только чисел второго десятка порядок называния составляющих их разрядных чисел и порядок записи не совпадает: сначала называются единицы (тринадцать), а пишется первым десяток (13). Эти особенности нумерации требуют того, чтобы числа второго десятка были рассмотрены отдельно.
Подготовительная работа к изучению нумерации чисел второго десятка проводится при повторении материала по теме «Десяток». С этой целью включаются упражнения в счете предметов с выходом за десяток к примеру, сколько учеников в первом ряду, во втором ряду? Так, например, можно предложить детям упражнения на развитие операции классификации и закрепления материала по теме «Десяток»: посмотрите на рисунок и определить общие признаки и свойства изображённых на нём предметах, чтобы получилось верным действие сложения.
рис. 1
Изучение устной нумерации чисел второго десятка начинается с формирования у детей понятия о десятке. Отсчитывая по 10 палочек и завязывая их в пучки, учащиеся узнают, что десять единиц образуют десяток. Затем, выполняя упражнения в счете десятков палочек, сложении и вычитании десятков с использованием палочек, дети убеждаются, что десятки можно считать, складывать и вычитать как простые единицы.
Далее рассматривается образование чисел от 11 до 20 из десятков и единиц и поясняются их названия.
Например, упражнение: глядя на рис. 2, классифицировать по общему признаку изображённые на нём предметы: по цвету, форме, размеру.
 Рис. 2
Рис. 2Мы предлагали учащимся положить 1 палочку на пучок-десяток палочек и посчитать, сколько всего палочек стало. Затем, опираясь на иллюстрацию, дети устанавливали десятичный состав полученного числа. Далее вспоминали, как получить следующее число, присоединяли к 11 палочкам еще 1 палочку и объясняли, что «две на десять» — это двенадцать, что число 12 состоит из 1 десятка и 2 единиц.
Так же мы рассматривали образование и название других чисел второго десятка и одновременно порядок их следования при счете.
Помимо палочек, в качестве наглядного пособия мы использовали полоски, на каждой из которых по 10 кружков (десятки), и полоски с 1, 2, 3, …, 9 кружками (единицы). При этом мы сравнивали их и классифицировали.
Натуральное следование чисел удобно иллюстрировать с помощью самодельных бумажных полосок длиной 20 см. Используя «ленту двадцати», дети устанавливают, какое число за каким следует, какому предшествует, между какими числами находится. Это формирует у них операцию сравнения. Например, каждый раз мы предлагали детям сравнить пучок-десяток и одну палочку с одиннадцатью отдельными палочками (двенадцатью, тринадцатью и т.д.).
Для закрепления знаний десятичного состава и натурального следования чисел в пределах 20 предлагают учащимся - сначала с опорой на наглядные пособия, а потом без них - такие упражнения: «Отсчитайте 15 палочек; узнайте, сколько это составляет десятков палочек и сколько отдельных палочек; возьмите 1 десяток палочек и еще 4 палочки. Сколько всего палочек взяли? Сколько десятков и единиц в числе 17? Какое число состоит из 1 десятка и 9 единиц? Положите 13 палочек, придвигайте теперь по одной палочке и называйте, сколько палочек становится (до 20—25); положите 17 палочек; откладывайте в сторону по одной и называйте, сколько палочек остается (до 7—8); начиная с числа 10 присчитывайте по одному и называйте полученные числа; отсчитывайте от 20 по одному, пока не получится 10».
Далее учащиеся знакомятся со второй единицей длины - дециметром как десятком сантиметров. Включаются упражнения в черчении и измерении отрезков, длина которых выражается как в единицах одного наименования (12 см, 15 см и т. п.), так и в единицах двух наименований (1 дм 5 см, 1 дм 8 см и т. п.). Опираясь на сравнение отрезков, дети постепенно овладевают умениями заменять крупные единицы мелкими (1 дм 3 см =13 см) и обратно (20 см =2 дм). При этом закрепляются знания десятичного состава. Например, 1 дм 3 см надо выразить в сантиметрах. Сравнивая, ученик рассуждает так: 1 дм—это 1 десяток сантиметров; 1 десяток и 3 см составляют 13см. Аналогично выражая 15см в дециметрах и сантиметрах, в числе 15 см выделяют 1 десяток сантиметров (т.е. 1 дм) и 5 см. подобные приёмы проводились нами на каждом уроке при изучении нового числа в пределах 20.
На следующем этапе приступают к изучению письменной нумерации. Чтобы раскрыть поместный принцип записи двузначных чисел, используют абак-таблицу с двумя рядами карманов: один ряд – 6 для палочек, другой - для разрезных цифр. Знакомя с пособием, учитель показывает, как ставят в верхних карманах палочки, когда их 5, 9, 10, 14 штук. Затем ученикам предлагают разложить в карманы, например, 15, 17 палочек.
Переходя к обозначению чисел, обязательно выясняют десятичный состав каждого числа и, опираясь на него, записывают, цифрами, сколько в этом числе десятков и сколько, кроме того, единиц. Сразу закрепляют полученные знания о принципе записи двузначных чисел: что обозначает цифра 7, которая стоит в записи числа 17 на первом месте справа, и что обозначает цифра 1, которая стоит на втором месте справа.
Аналогично рассматривают еще несколько чисел, а затем дети записывают числа в своих тетрадях в таблицах с надписями «десятки» и «единицы» и объясняют значение каждой цифры.
Особо рассматривается запись чисел 10 и 20: цифра 1 (2) показывает, что в числе содержится 1 десяток (2 десятка), цифра 0 - в числе отсутствуют единицы.
Упражняясь в записи чисел, учащиеся закрепляют знания десятичного состава и натурального следования чисел в пределах 20. Например, учитель предлагает записать число, которое состоит и:) 1 десятка и 9 единиц; записать число, которое следует при счете за числом 19 (предшествует числу 11); которое больше (меньше) на 1 числа 15; решить примеры 12+1, 18-1 и записать ответы. Дети записывают ответы и объясняют, почему они записали то или иное число. Так, выполняя последнее задание, учащиеся поясняют: к 12 прибавить 1, получится 13, потому что, прибавляя к числу 1, получаем число, которое следует за ним при счете.
Опираясь на наглядные пособия, учащиеся знакомятся со случаями сложения и вычитания вида: 10+5, 15-5, 15-10. Выполняя такие вычисления, учащиеся закрепляют знания десятичного состава чисел: например, 10+5, десять - это 1 десяток, 1 десяток и 5 единиц составляют число 15; 15 - 10, пятнадцать - это 1 десяток и 5 единиц, вычтем 10, или 1 десяток, получится 5 единиц.
Сопоставляя и сравнивая числа, учащиеся устанавливают, что для записи числа, состоящего из единиц, требуется одна цифра (один знак); для записи числа, состоящего из десятков или десятков и единиц, требуется две цифры (два знака). Вводятся термины «однозначные» и «двузначные» числа. Дети приводят примеры однозначных и двузначных чисел, выполняют упражнения на различение однозначных и двузначных чисел, например: «Выпишите из ряда чисел сначала однозначные, а потом двузначные числа: 2, 13, 8, 17» 15, 6, 11, 10; запишите 4 любых однозначных числа и увеличьте каждое на 10. Какие числа у вас получились, как можно их назвать?
С целью систематизации знаний по нумерации полезно в конце работы над темой включать задания по характеристике заданных чисел. Характеризуя, например, число 13, учащиеся могут назвать его десятичный состав (в этом числе 1 дес. и 3 ед., или 1 ед. II разряда и 3 ед. I разряда), сказать о месте этого числа в натуральной последовательности (число 13 называют при счете после 12 и перед 14). Также полезно проводить задания на сравнение этих чисел с рисунками, изображенные на которых предметы соответствуют этому числу.
В результате изучения темы «Сложение и вычитание» учащиеся должны научиться осознанно выполнять сложение и вычитание любых чисел в пределах 100, твердо усвоить табличные случаи сложения и вычитания с переходом через десяток, а также ряд теоретических вопросов.
Как и при изучении первого десятка, приемы сложения и вычитания в пределах 20 раскрываются в органической связи с изучением теоретического материала. При таком подходе лучше усваиваются вопросы теории, так как они находят применение, и быстрее формируются более осознанные вычислительные навыки.
Анализ приемов сложения и вычитания чисел в пределах 20 показывает, что для их осознанного выполнения учащиеся должны хорошо знать нумерацию чисел в пределах 20, твердо знать таблицу сложения и соответствующие случаи вычитания в пределах 10 и, кроме того, усвоить следующие свойства действий сложения и вычитания: прибавление числа к сумме, вычитание числа из суммы, прибавление суммы к числу, вычитание суммы из числа, прибавление суммы к сумме и вычитание суммы из суммы.
Сложение и вычитание рассматриваются в таком порядке.
Рассмотрим подробнее методику изучения свойств и вычислительных приемов.
На двух-трех уроках, ученики проговаривают объяснение вслух, а затем про себя. В результате упражнений у учащихся постепенно вырабатывается навык.
Введению свойства прибавления числа к сумме должна предшествовать специальная подготовительная работа, в результате которой учащиеся знакомятся с математическими выражениями «сумма чисел...» и «разность чисел...», учатся читать и записывать выражения со скобками, заменять двузначные неразрядные числа суммой их разрядных слагаемых. Эти вопросы рассматриваются при изучении сложения и вычитания чисел в пределах 10 и нумерации чисел в пределах 20.
Изучение каждого свойства строится примерно по одному плану: сначала, используя наглядные пособия, надо раскрыть суть самого свойства, затем научить детей применять его при выполнении различных упражнений учебного характера, и, наконец, научить, пользуясь знанием свойства, находить рациональные приемы вычислений с учетом особенностей каждого конкретного случая.
Рассмотрим, как можно провести ознакомление детей со свойством прибавления числа к сумме.
Раскрывая суть свойства, надо показать детям, что число к сумме можно прибавлять различными способами: можно вычислить сумму и к полученному результату прибавить число, можно прибавить число к первому слагаемому и к полученному результату прибавить второе слагаемое, а можно прибавить число ко второму слагаемому и полученный результат сложить с первым слагаемым. Везде при этом у первоклассников формируется операции сравнения нового числа с другим, ранее изученным.
Покажем, как это можно сделать.
Учитель. Пишет на доске выражение (5+3)+2. Прочитайте пример. (К сумме чисел 5 и 3 прибавить 2.) Назовите сумму. (5 плюс 3.) Назовите первое слагаемое этой суммы. (5.) Назовите второе слагаемое. (3.) Назовите число, которое надо прибавить к этой сумме. (2.) Как найти результат? (Вычислю сумму, получится 8; прибавлю 2, получится 10.)
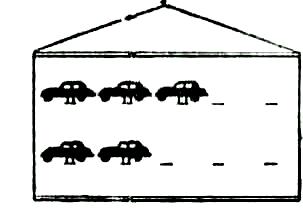
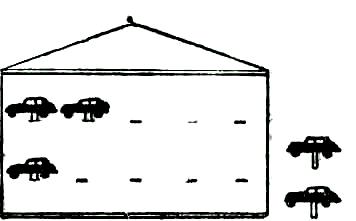
рис.3.
На доске запись: (5+3)+2=8+2=10.
Сегодня вы научитесь прибавлять число к сумме и другими способами.
Учитель. (Вывешивает на доске рисунки двух гаражей и предлагает ученикам приготовить прямоугольники голубого, зеленого и красного цветов, вырезанные из бумаги). Это гаражи. Число машин в первом гараже будет изображать первое слагаемое. Сколько машин надо поставить в первый гараж? (5.)
Учитель. (Вставляет в прорези 5 машин голубого цвета, вырезанные из картона, а учащиеся раскладывают на партах 5 голубых прямоугольников). Число машин во втором гараже будет изображать второе слагаемое. Сколько машин поставим во второй гараж? (3.)
Учитель (ставит во второй гараж 3 зеленые машины, а дети раскладывают на партах 3 зеленых прямоугольника). Приехали еще две машины (прикрепляют к доске две красные машины, а учащиеся кладут на парту два красных прямоугольника).
На доске располагаются рисунки (рис. 1).
Учитель. Красные машины надо поставить в гараж. В какой гараж их можно поставить? (В первый или во второй), доставим их в первый гараж. (Учитель «ставит» машины в первый гараж, а дети придвигают красные прямоугольники к голубым). Как теперь узнаем, сколько всего машин?
Дети. К 5 прибавить 2, получится 7, и еще прибавить 3, получится 10.
Учитель. Да, число 2 мы прибавили к 5, первому слагаемому, потом к полученному результату, к 7, прибавили второе слагаемое 3. Сравните ответы.
Дети. Получилось тоже 10.
Учитель. Если получилось столько же, сколько при решении первым способом, значит, можно прибавлять число к сумме и таким способом. Кто расскажет, как мы сейчас прибавляли число к сумме?
Дети. (рассказывают.)
Аналогичным образом с использованием тех же пособий раскрывается еще один способ: можно прибавить число ко второму слагаемому - к 3 и полученный результат сложить с первым слагаемым - с 5.
Учитель. Сколько способов прибавления числа к сумме мы рассмотрели?
Дети. Три.
Учитель. Да, три способа: можно решить пример так, как и раньше это делали - вычислить сумму чисел 5 и 3 и к результату, к 8, прибавить число 2; можно прибавить число 2 к первому слагаемому, к 5, и к полученному результату, к 7, прибавить второе слагаемое 3; а можно прибавить число 2 ко второму слагаемому, к 3, и полученный результат, 5, сложить с первым слагаемым - с 5.
Далее так же рассматривается решение тремя способами еще одного примера на прибавление числа к сумме. При этом используется то же наглядное пособие.
При раскрытии свойства можно использовать и другие пособия, например: в ведра вливать воду литрами, в конверты вкладывать открытки, в тарелки раскладывать фрукты и т. п.
На следующем уроке, рассматривая три способа прибавления числа к сумме, одновременно с использованием наглядных пособий выполняют развернутую запись. Эту запись учитель выполняет на доске или на плакате, а учащиеся в тетрадях. Например, решение тремя способами примера (4+2)+8 следует записать следующим образом:
1) (4+2)+3=6+3=9;
2) (4+2)+3= (4+3)+2=7+2=9;
3) (4+2)+3=4+(2+3)=4+5=9.
Выполнение каждой записи учащиеся сопровождают объяснением сначала под руководством учителя, а потом самостоятельно. На этом этапе не следует требовать от детей обобщенной формулировки правила прибавления числа к сумме, достаточно, чтобы они умели объяснять решение различными способами данных конкретных примеров.
Для подготовки учащихся к приему вычитания, основанному на знании таблицы сложения, надо включать специальные упражнения, направленные на усвоение состава чисел второго десятка. Так, пользуясь составленной таблицей, учащиеся называют, суммой каких двух однозначных чисел является, например, число 11 (12, 13, ..., 18), и записывают 11=9+2, 11=8+3 и т.д.
После изучения свойства вычитания суммы из числа по той же методике, как и другие свойства, рассматривают вычитание вида 12-5.
Для этого случая вычитания целесообразно рассмотреть три приема: первый основывается на использовании свойства вычитания суммы из числа, второй - на использовании свойства вычитания числа из суммы, а третий - на знании состава чисел второго десятка и связи между суммой и слагаемыми.
Подготовкой к введению первого приема будет решение удобным способом примеров вида 13-(3+2). При ознакомлении с приемом используется то же наборное полотно, которое применялось при раскрытии приема сложения вида 9+5 (см. рис. 2).
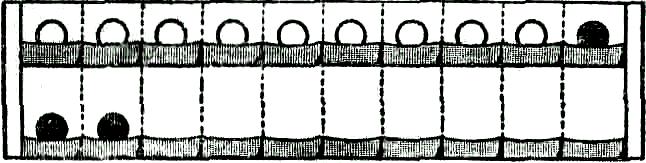
Предлагается решить пример 12-5. Каждый ученик у себя на парте, а один из них на доске, откладывает на наборном полотне 12 «кружков. Учитель спрашивает, как удобнее вычесть 5 из 12. Ученики предложат вычесть сначала 2 (вынимают 2 кружка), а потом еще 3 (вынимают 3 кружка). Выясняется, что число 5 заменили суммой удобных слагаемых 2 и 3, вычли сначала одно слагаемое, а потом из полученного результата другое.
Запись: 12-5= 12-(2+3) =(12-2)-3=7.
При этом ученик ведет объяснение, используя операцию сравнения руководствуясь ранее данным планом: «Заменю число 5 суммой удобных слагаемых 2 и 3; получился пример: из 12 вычесть сумму чисел 2 и 3; удобнее сначала вычесть 2, первое слагаемое, а из полученного результата, из 10, вычесть 3, второе слагаемое, получится 7».
Не исключено, что сами дети предложат прием замены уменьшаемого суммой разрядных слагаемых: 12-5= (10+2)-5= (10-5)+2=7
В этом случае после коллективного разбора надо сказать детям, что можно пользоваться и таким способом. Если ученики сами не придут к этому способу, то учителю следует ввести его, но несколько позднее.
В качестве подготовки к приему, основанному на знании состава чисел второго десятка, надо повторить аналогичный прием с числами первого десятка, больше уделить внимания работе над составом чисел второго десятка и провести ряд специальных упражнений на нахождение результатов вычитания по соответствующему результату сложения (например, найти результаты второго и третьего примеров по результату первого: 7+5, 12-7, 12-5). После такой подготовки учащиеся сами находят для случая вида 14—5 третий прием: 14 - это сумма чисел 5 и 9; если из 14 вычесть 5, получится 9.
После введения приемов, как и в других случаях, ведется работа по формированию вычислительных навыков.
Как показал опыт, в это время учащиеся смешивают приемы для случаев: 13-4 и 14-3, т. е. прием, основанный на свойстве вычитания суммы из числа, и прием, основанный на свойстве вычитания числа из суммы. Чтобы предупредить ошибки такого рода, полезно рассмотреть эти случаи вычитания в противопоставлении, выяснив, чем главным отличаются приемы (в первом случае из 13 вычли 3 и из результата вычли 1, а во втором случае из 4 вычли 3 и результат (1) прибавили к 10).
В целях предупреждения ошибок в вычислениях необходимо научить детей выполнять проверку сложения и вычитания и, что очень важно, воспитать у них привычку проверять решение постоянно. При изучении рассматриваемой темы надо ознакомить детей со способом проверки, который основывается на связи между компонентами и результатом действий сложения и вычитания: для проверки сложения вычитают из полученной суммы одно из слагаемых; если получится другое слагаемое, то можно считать, что пример решен правильно; для проверки вычитания надо к полученной разности прибавить вычитаемое; если пример решен правильно, то получится уменьшаемое, или надо из уменьшаемого вычесть полученную разность, тогда, если пример решен правильно, получится вычитаемое. Кроме этого способа, как и при сложении и вычитании чисел первого десятка, надо использовать способ прикидки результата (сравнивать полученный результат с компонентами). Для ряда случаев можно выполнять проверку путем решения примеров разными способами: если при решении разными способами получатся одинаковые результаты, то можно считать, что пример решен правильно.
Итак, при использовании специальных заданий на уроках математики, в которых детей знакомят с составляющими действиями операций сравнения и классификации, повышается уровень владения этими операциями.
3.3. Контрольный этап эксперимента
Цель контрольного этапа состояла в выявлении эффективности проведённых упражнений и заданий на классификацию и сравнение.
Д

 ля выявления эффективности разработанной нами методики по истечению вышеуказанного срока был проведен контрольный срез №2 на третьем этапе эксперимента.
ля выявления эффективности разработанной нами методики по истечению вышеуказанного срока был проведен контрольный срез №2 на третьем этапе эксперимента.1



 .Сравни: а)
.Сравни: а)б) 6 + 4 и 6
в) 7 + 2 = 9 и 7 + 3 = 10
2


 .Разложи фигуры (и укажи номера) на две группы:
.Разложи фигуры (и укажи номера) на две группы:а


 )
)  1 2 3 4 5 6 7
1 2 3 4 5 6 7б
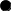
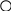
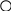
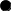

 )
) Испытуемым предлагались задания, аналогичные заданиям, используемым на констатирующем этапе эксперимента: сохранилась формулировка, но изменились объекты, с которыми оперируют учащиеся.
Результаты отражены в таблице 3, 4.
Таблица 3
Выявление уровня сформированности операции сравнения
| классы | Констатирующий этап | Контрольный этап | ||||||
| Низкий | Ниже среднего | средний | высокий | Низкий | Ниже среднего | средний | высокий | |
| экспериментальный | 20% | 20% | 35% | 25% | 15% | 10% | 45% | 30% |
| контрольный | 10% | 15% | 40% | 35% | 10% | 30% | 35% | 25% |
Таблица 4


 Если фигуры правильно разделены по группам – 2 балла
Если фигуры правильно разделены по группам – 2 балла