8-15 дәріс тезистері (1). Дріс жоспары Тжірибелік деректер сипаты

• Название: Дріс жоспары Тжірибелік деректер сипаты
• Дата: 19.05.2022
• Размер: 1.65 Mb.
• Имя файла: 8-15 дәріс тезистері (1).docx
• Тип: Документы; #538787
• страница: 7 из 7

Тақырып №15. Дербес туындылармен теңдеулер. Айырымдық схемалар теориясының элементтері.

Дәріс жоспары:

1. 
   Кіріспе ескертулер
   
2. 
   Айырымдық схемалар құру туралы
   
3. 
   Жинақтылық. Аппроксимация. Тұрақтылық.
   

1. Бастапқы ескертулер. Бұл бөлім дербес туындылары бар теңдеулер үшін есептерді шешудің сандық әдістеріне арналған. Бұл қазіргі уақытта дербес туындылары бар теңдеулермен модельделген қолданбалы есептер шешілетін әдістердің негізгі класы. Сандық әдістер жоғары қуатты компьютерлердің болуын талап етеді, яғни.үлкен жады және жоғары есептеу жылдамдығы бар.

Сандық әдістердің ішінде айырымдық әдістер кең таралған. Қарапайым дифференциалдық теңдеулер сияқты, олар қарастырылатын аймақта кейбір айырымдық торды енгізуге негізделген. Туынды мәндері, бастапқы және шекаралық шарттар тор түйіндеріндегі функциялардың мәндері арқылы өрнектеледі, нәтижесінде айырымдық схема деп аталатын алгебралық теңдеулер жүйесі пайда болады. Осы теңдеулер жүйесін шеше отырып, тордың түйіндерінен қажетті функциялардың мәндеріне жуық деп саналатын торлық функциялардың мәндерін табуға болады.

Осы бөлімде көрсетілген сандық әдістер әртүрлі есептерге қолданылады. Біз туындыларға қатысты сызықтық бірінші және екінші ретті теңдеулер үшін жеткілікті тар есептер класын қарастырамыз. (Еске салайық, дифференциалдық теңдеудің реті ең үлкен туындының реті бойынша анықталады.) Екі тәуелсіз айнымалы х, у жағдайында бұл теңдеулерді келесі түрде жазуға болады:

(1)

Мұнда u = u(х,у) — iзделiніп отырған функция. а, b, с, d, e, f коэффициенттері және g оң жақ бөлігі, жалпы айтқанда, х, у айнымалыларынан және iзделiніп отырған функциядан тәуелді болуы мүмкін. Осыған орай теңдеу (8.1) төмендегідей болуы мүмкін: а) тұрақты коэффициенттермен; б) сызықты, егер g u-дан сызықты тәуелдi болса, ал коэффициенттер тек қана х,у тәуелдi болса; в) егер коэффициенттер u -ден тәуелдi болса квазисызықты, бұл (8.1) теңдеудiң ең жалпы көрiнiсi.

Коэффициенттер арасындағы қатынастан тәуелді теңдеулердiң әр түрлi түрлерi болады. Олардың кейбірін қарастырайық.

a = b = c = f = = 0, мұнда бiрiншi ретті теңдеудің



тасымалдау теңдеуі деп аталатын түрі пайда болады. Бұл теңдеу тәжірибе жүзiнде айнымалылардың бірі t уақыты бола алады. Онда оны эволюциялық теңдеу деп те атайды.

Егер а,в,с - ның коэффициенттерінiң бiрi, нөлден айырмашылығы болса, онда (8.1 ) екiншi реттi теңдеу болып табылады. Дискриминант D = b² — ас таңбасына байланысты - ол үш түрлердiң бiрiне жатуы мүмкін: гиперболалық (D > 0), параболалық (D = 0) немесе эллипстік (D < 0).

Екiншi ретті дербес туындыларыбар теңдеулерiге мысалдар келтiрейік:

толқындық теңдеу (гиперболалық):



жылуөткiзу немесе диффузия теңдеуi (параболалық)



Лаплас теңдеуі (эллиптикалық)



Егер соңғы теңдеудiң оң бөлiгi нөлден айырмасы болса, онда ол Пуассонның теңдеуi деп аталады. Келтiрiлген теңдеулер математикалық физика теңдеулерідеп аталады. Олардың шешiмiне көп қолданбалы есептердi жатқызуға болады. Көрcетiлген теңдеулердiң шешiмiнiң сандық әдiстерiн талқыламастан бұрын, айырма схемалардың құрастыруының негiзгi мәселелерiн қарап шығамыз.

2. Айырымдық схемаларды құру туралы. Жоғарыда айтылғандай, дербес туындылары бар теңдеулерді шешудің айырымдық схемаларын құру қарастырылып отырған кеңістікте торды енгізуге негізделген. Тор түйіндері-есептеу нүктелері.

Екі өлшемді жағдайда Г шекарасы бар қарапайым тікбұрышты G(x, y) облсының мысалы 8.1 -суретте көрсетілген. а ≤ х ≤ b, с ≤ у ≤ d тіктөртбұрышының жақтары x_i = а + ih₁ (i = 0,1,..., I) және y_j = с + jh₂ (j = 0,1,..., J) нүктелерімен элементар кесінділерге бөлінеді. Осы нүктелер арқылы тікбұрышты ұяшықтары бар торды құрайтын, x = const және у = const координаталық түзулердің екі тобы жүзеге асырылады. Нөмірі (i, j) болатын, оның кез келген түйіні [x_i, y_j] координаттарымен анықталады. Себебі 8.1-суретте көрсетілген тордың барлық ұяшықтары бірдей, мұндай тор теңөлшемді деп аталады.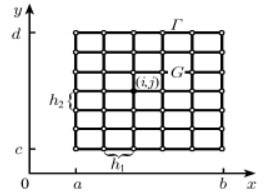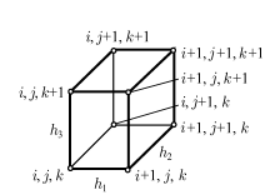



8.1-сурет. Тікбұрышты тор 8.2-сурет. Тор элементі

Сол сияқты, екіден артық өлшемі бар көп өлшемді облыстар үшін торлар енгізіледі. 8.2-суретте үш өлшемді облыс үшін тікбұрышты параллелепипед түрінде тор элементі көрсетілген.Тікбұрышты торлар есептеу алгоритмін ұйымдастыруда ең ыңғайлы. Сонымен қатар, кейбір тізбектер күрделі пішінді ұяшықтары бар торларды пайдаланады: үшбұрышты, төртбұрышты (тікбұрышты емес), алтыбұрышты және т. б.

G облысының Г шекарасында орналасқан тор түйіндері шекаралық түйіндер деп аталады. Барлық қалған түйіндер ішкі болып табылады. Есепті қою кезіндегі бастапқы және шекаралық шарттар есептеу облысының шекарасында тұжырымдалғандықтан, оларды тордың шекаралық түйіндерінде берілген деп санауға болады.

Айырымдық схеманы құру үшін, кәдімгі дифференциалдық теңдеулер сияқты, теңдеудегі дербес туындылар белгілі бір шаблон бойынша ақырлы-айырымдық қатынастармен ауыстырылады (3-т.§1). Бұл жағдайда қалаған функцияның нақты мәндері айырымдық тор түйіндеріндегі тор функциясының мәндерімен ауыстырылады.

Мысал ретінде берілген бастапқы және шекаралық шарттарда жылу өткізгіштік теңдеуін шешу үшін кейбір айырымдық схемаларды құрайық. Аралас шектік есепті келесі түрде жазамыз: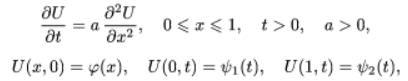

(8.2)

мұнда φ(х) — U температурасының бастапқы таралуы (t = 0 кезінде); ψ₁(t), ψ₂ (t) — t уақыттың кез келген сәтінде қарастырылатын (х = 0, 1) кесіндінің ұштарындағы температураның таралуы. Бастапқы және шекаралық шарттар келісілуі тиіс, яғни U(0,0) = φ (0) = ψ₁ (0), U(1,0) = φ (1) = ψ₂ (0).

x_i = ih (i = 0,1,..., I), t_j = jτ (j = 0,1,...) координаталық сызықтарының көмегімен теңөлшемді тік бұрышты торды енгіземіз; h және τ — х және t бағыттары бойынша сәйкес тор қадамдары. арқылы тор түйіндеріндегі функция мәндерін белгілейміз. Бұл мәндер айырымдық схеманы құрайтын теңдеулерді қанағаттандыратын, тор функциясының тиісті мәндерімен алмастырылады. ¹⁾.

¹⁾ Часто верхний индекс заключают в скобки, чтобы не путать его с показателем степени. Здесь и далее скобки для краткости опущены.

(8.2) бастапқы теңдеуде шекті айырымдық қатынастары көмегімен, қажетті функцияның дербес туындыларын алмастыра отырып, біз келесі айырымдық схеманы аламыз: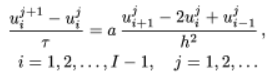

(8.3)

Осы схеманың жазбасында әр түйін үшін 8.4, а -суретте көрсетілген шаблон қолданылады.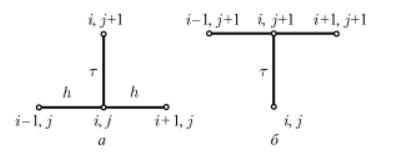



8.4 -сурет. Шаблондар

Шекаралық түйіндердегі мәндер шекаралық шарттардан табылады

(8.5)

t = const кезіндегі түйіндердің жиынтығы, яғни бекітілген j мәні кезінде қабат деп аталады (немесе t айнымалысы уақытқа сәйкес болғандықтан, уақыт қабаты). (3) схемасы және j-ші қабаттағы сәйкес мәндері арқылы (j+1)-ші қабаттағы (i = 1, 2,...,I-1) мәндерін тізбекті түрде табуға мүмкіндік береді. Мұндай схемалар айқын деп аталады..

j = 1 кезінде (3) схема бойынша есептеуді бастау үшін j = 0 кезінде бастапқы қабаттағы шешімді білу қажет. Ол (2) бастапқы шартпен анықталады, ол келесі түрде жазылады

(8.6)

Қарастырылған мысалда біз екі қабатты схемаларды аламыз, әр айырымдық теңдеуге екі қабаттан тұратын функцияның мәндері кіреді: төменгі, онда шешім табылған және жоғарғы, оның түйіндерінде шешім ізделеді.

Айырымдық схемаларды құрудың қарастырылып отырған әдісін қолдана отырып, теңдеуге кіретін жеке дербес туындылар тор функциясы үшін (немесе торлық өрнектер) шекті айырымдық қатынастармен алмастырылған кезде, көп қабатты схемалар, сондай-ақ жоғары дәлдіктегі схемалар құрылуы мүмкін.

Айырымдық теңдеулерді алудың бұл әдісі ең қарапайым, сондықтан сандық әдістерді жасауда кеңінен қолданылатынына қарамастан, айырымдық схемаларды құрудың басқа тәсілдері де бар.