Е. М. Четыркин финансовая математика
 Скачать 4.63 Mb. Скачать 4.63 Mb.
|
Ничего принципиально не меняется, если взнос производится не разовым платежом, а в рассрочку. Пусть предусматривается пожизненная выплата пенсий и рассрочка взносов в течение к лет. Изменение резерва во времени изображено на рис. 17.6. Общий срок действия страхового полиса в этом случае можно разбить на три периода. В первом, в возрасте от х до х + к, осуществляются взносы и происходит ускоренное накопление, во втором, от х + к и до возраста L, сумма резерва увеличивается только за счет процентов, в третьем средства расходуются на выплату пенсий, причем на остаток средств начисляются проценты. В "финальном" возрасте со после выплаты пенсии резерв равен нулю. Аналогичное можно сказать и относительно динамики средств на персональном счете, кроме момента полного исчерпания средств, который происходит в возрасте (А < ш). 372 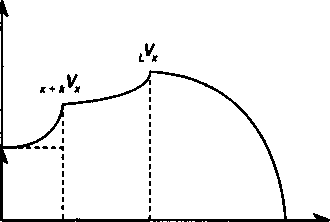 Резерв Р* хx-i-fr L оВозраст Рис 17.6 Ограничимся случаем, когда пенсии и взносы выплачиваются раз в году пренумерандо и не учитывается дополнительный инвестиционный доход, выплата которого предусматривается в некоторых пенсионных фондах. Запишем в общем виде формулу величины резерва в момент х + г. где Ax¥t— современная стоимость пенсионных выплат, производимых после возраста х + /, ax^t— стоимость немедленного ограниченного страхового аннуитета пренумерандо в возрасте х + / лет, Рх— годовой размер премии, установленный в возрасте х лет. Формула (17.31), как видим, предполагает определение будущих (ожидаемых) поступлений. Ее результат представляет собой "чистые" обязательства страховщика перед участником в возрасте х + / лет. Подобный способ получил название прямой метод определения резерва. Определим резерв для случая, когда пенсия пожизненная, R = 1, нетто-премия равна Рхв расчете на денежную единицу пенсии, пенсия и премии выплачиваются пренумерандо. В этом случае для первого периода (/ < к) находим / К * n-t\dx Рх х йх:Щ><17-32) где п = L — х — временной интервал от х до L лет, ^^ах— стоимость отложенного пожизненного страхового аннуитета пренумерандо, dx.jzji — стоимость немедленного ограниченного аннуитета. 373 Величина Рхнаходится на основе принципа эквивалентности обязательств страховщика и страхователя. Если R = 1, то из равенства этих обязательств следует, что 0VX= 0 и нетто-пре-мия находится как соотношение двух страховых аннуитетов — отложенного пожизненного и немедленного ограниченного, а именно: В свою очередь /^ = -7^4 (17.33) йх:к] NL. Ц-*и Л D' ax:k]D х х Подставив в (17.32) приведенные формулы для страховых аннуитетов и нетто-премии, получим для первого периода у_ "lnl^ *u*U _ ^x+tNx"" ^х+к^x+t (17.34) ^L Л ^x+t ^х+к &x+t \ Nx Nx+k Для второго периода (к < t < п) находим "l ux+t Наконец, для третьего периода (t > n) получим NxH .V^-f-.(17.36) Приведенные выше методы расчета резерва, разумеется, не охватывают весь спектр возможных способов выплат премий и пенсий. Однако ничего принципиально не меняется, если скажем, вместо пенсий пренумерандо выплачиваются пенсии пост-нумерандо, а вместо годовых пенсий или взносов — ежемесячные, вместо пожизненных пенсий выплачиваются ограничен- 374 ные и т.д. Разумеется, в этих случаях несколько изменяется техника расчетов, общие принципы расчетов остаются без изменений. ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
ПРИЛОЖЕНИЕ Таблицы
Таблица 1 Порядковые номера дней в году
|
