Е. М. Четыркин финансовая математика

• Название: Е. М. Четыркин финансовая математика
• Анкор: chetyrkin_e_m_finansovaya_matematika.doc
• Дата: 22.04.2017
• Размер: 4.63 Mb.
• Имя файла: chetyrkin_e_m_finansovaya_matematika.doc
• Тип: Учебник; #4971
• страница: 29 из 58

§17.6. Страховые резервы в личном страховании

Важнейшим фактором, обеспечивающим надежность в рабо­те страховых организаций, является определение размеров ре­зервов как для отдельных застрахованных, так и для их групп и в целом по всем полисам страховой организации.

Под резервом понимается современная стоимость "чистых" обязательств страховой организации. Сумму резерва можно оп­ределить двумя методами — прямым (или проспективным) и обратным (ретроспективным). Оба метода дают одинаковые ре­зультаты. При прямом методе резерв равен современной стоимо­сти выплат, которые обязан осуществить страховщик, за выче­том современной стоимости ожидаемых взносов страхователя.

В связи с термином "резерв" необходимо сделать отступле­ние от обсуждения основной проблемы главы. Дело в том, что этот термин, трактуемый как чистые обязательства страховщи­ка, является узко профессиональным. Он уже более века как за­креплен в отечественном и западном (reserve) страховании.

Главное, на что надо здесь обратить внимание, — это то, что резерв в указанном выше смысле означает обязательства, а не реальные накопления (активы). Резерв — важный аналитиче­ский показатель: для того, чтобы обязательства перед страхова­телями были выполнены, резерву должны соответствовать не­которые активы, равные или превышающие размеры резерва. Формирование таких активов является обязательной, нормаль­ной функцией страховщика и не связано с покрытием расходов в каких-либо чрезвычайных обстоятельствах

Вместе с тем, в экономической да и других областях деятель­ности, применяется иное понимание термина резерв — как не­которого запаса или фонда, денежного или вещественного, предназначенного для покрытия расходов или иных потребно­стей в непредвиденных ситуациях. Например, продовольствен­ный резерв, резерв мощности двигателя, резерв главного ко­мандования и т.д. Иначе говоря, такие резервы не являются обязательствами.

Как видим, существует кардинальное различие в понимании обсуждаемого термина. Смешение понятий, которое несомнен­но мешает практической работе, отразилось на текстах соответ­ствующих российских законов. Во всех законах о страховой де­ятельности резерв трактуется не в специальном страховом, а в широком понимании, как реальные накопления, активы. На-

365

пример, в одном из законов читаем: "Страховщик вправе инве­стировать или иным способом размещать страховые резервы...". Однако обязательства нельзя инвестировать.

Возникла в некотором роде тупиковая ситуация. Для того чтобы устранить указанное смешение понятий, назовем мате­матическим резервом, или кратко резервом, величину, получае­мую по приведенному выше определению. В свою очередь под страховым резервом будем понимать активы, предназначенные для выполнения обязательств страховщика.

Перейдем к методу расчета резерва. Резерв можно опреде­лить на любой момент действия страхового контракта. Для на­чала определим его на начало действия договора до первой вы­платы премии. В случае, когда предусматриваются ежегодные пожизненные взносы пренумерандо в размере Р_х, получим по определению для прямого метода

0^Ух = ^Ах ^Рх^хйх = °>О⁷-¹⁶)

где ₀V_X— размер резерва для застрахованного в возрасте х лет, А_х— современная стоимость каких-либо страховых обяза­тельств.

Если резерв определяется для тех же условий, но на момент / после начала страхования, то

Л-^l-^^xM- <¹⁷-¹⁷)

Страхование на дожитие. Приведенное выше определение ре­зерва можно конкретизировать применительно к различным ус­ловиям и применяемым схемам страхования. Как и при обсуж­дении других проблем начнем с частного случая личного стра­хования — определения резерва при страховании на дожитие. В этом виде страхования предусматривается только единовремен­ная премия. Соответствующая сумма зачисляется на счет участ­ника и служит первоначальным резервом, в связи с чем форму­ла (17.17) упрощается до

Положим, что страховая сумма равна единице, R = 1, тогда

Л - 4*, - "Г" * *" " д^ ^(Ш9)-

*x+t ^ux+t

366

Нетрудно убедиться в том, что современная стоимость обя­зательств в данном виде страхования увеличивается во времени, так как по мере роста / знаменатель уменьшается.

В некоторых видах личного страхования, например пенсион­ном, оговаривается необходимость ведения персональных сче­тов застрахованных. Как будет показано ниже, средства, накоп­ленные на персональном счете отдельного застрахованного, не идентичны резерву. В связи с этим необходимо отчетливо пред­ставлять разницу между этими понятиями. В чисто иллюстра­тивных целях проследим, как изменяется во времени сумма на воображаемом (в данном виде страхования такие счета не ве­дутся) персональном счете застрахованного (величина S) и ре­зерв (_tV_x) при страховании на дожитие.

На сумму единовременного взноса наращиваются проценты за соответствующий срок. В итоге при R = 1 на счете участни­ка в момент / находится сумма S_t:

где _пЕ_х— размер премии по страхованию на дожитие (см. (17.1)).

Для момента / > О имеем S_f < _tV_x. Таким образом, наращен­ная сумма на персональном счете застрахованного меньше резерва на один и тот же момент времени, за исключением начального.

Из соотношения _tV_xи S_tтакже следует, что

D_xxv<l_x1

_{Л-*г^—-$*-f--$*-r-'} ⁽¹⁷_'^2,)

где _tp_x— вероятность дожития лица в возрасте х лет до возрас­та X + /.

На рис. 17.4 отражена динамика указанных величин в зави­симости от срока /. Чем ближе момент оценки резерва ко вре­мени погашения обязательства, тем больше разность между суммой на счете и резервом.

Важно понять причину расхождения между полученными выше показателями. Дело в том, что резерв увеличивается не только за счет накопленных процентов (на персональном сче­те), но и в силу солидарной ответственности застрахованных, т.е. за счет тех участников, которые не дожили до возраста х +

367

+ и Из сказанного следует, что общий размер резерва для дожив­ших до возраста х + / равен сумме средств на персональных сче­тах всех участников — доживших и не доживших до этого воз­раста.




S₀ "ям

накопления

Возраст

ПРИМЕР 17.10. Мужчина в возрасте 50 лет страхуется на дожи­тие до 60 лет, страховая сумма Я = 1000 денежных единиц. Пусть коммутационные функции определены для 9% и условий, учтен­ных в табл.12 Приложения. В этом случае сумма взноса и резерв на начало срока составит

060 389,17

Ъ - 10^50 = ЮОО-^ = 1000^^-= 345,98. Спустя один год на счете окажется наращенная сумма

S, = 345,98 х 1,09 = 377,12. В то же время резерв составит

60
,1^ = 1000-^ = 1000

'51

389,17

1017,4

= 382.51

или по формуле (17.21)

1 'so 83 640

,1^0= 377,12 х = 377,12 х = 377.12 х


82 461
^{1 ю} iPso '

= 382,51.

Таким образом, прирост резерва за один год за счет солидар­ности застрахованных равен 382,51 - 377,12 = 5,39. Динамика средств на счете и размеров резерва показана в следующей таб­лице.

368

t	0	5	10
s, У*>	345.98 345.98	532,33 625.77	819,06 1000.00

Как видим, на индивидуальном счете к концу срока страхова­ния средств меньше необходимых 1000 единиц. Однако следует учесть, что из 100 застрахованных в указанном возрасте соглас­но таблице смертности доживут до 60 лет только 82 человека, по­этому накопленные средства всех застрахованных окажутся дос­таточными для них.

Интересно выделить влияние факторов на размер резерва. Для этого найдем отношение размеров резерва для двух первых лет накопления для страхования на дожитие:


А

где р_х— вероятность прожить один год после возраста х лет. Аналогичным образом определим динамику резерва за / лет:



х+п

^ух+\

х+п

'х+\

lv^x

X

/.

,JC+I

*x+V

= -7(1 + 0,

Рх

Л 1

(17.22)

_Y ⁼ _"7^{(1 + /y}_-

0 ^Ух/Рх

Из сказанного выше следует, что размеры резерва можно оп­ределять и последовательно как

(17.23)

Как следует из полученного соотношения, резерв увеличива­ется быстрее, чем идет наращение за счет процентов, так как _tp_x< 1. Причем рост процентной ставки ускоряет накопление резерва, а увеличение вероятности дожития сокращает его.

Математический резерв при страховании жизни в случае, ко­гда это страхование оплачивается разовым взносом, формиру­ется аналогично тому, как было показано выше для страхова­ния на дожитие.

Страхование пенсии. Кратко остановимся на определении ре­зерва для еще одного вида личного страхования — индивиду­ального страхования пожизненной пенсии с единовременной

369

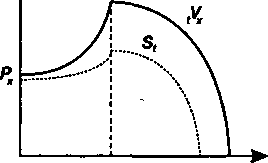
выплатой взноса. Динамика резерва для этого случая показана на рис 17.5. Обозначения на нем имеют следующее содержание:

Р_х— размер единовременного взноса, L — возраст выхода на пенсию,

h — возраст, в котором исчерпываются средства на персо­нальном счете застрахованного, со — предельный возраст.

Резерв, накопления



хL /?о) Возраст

Рис. 17.5

Весь период от возраста х до предельного возраста можно разделить на два временных отрезка. В первом, до начала вы­плат пенсии, происходит накопление резерва, во втором — на­копление сопровождается расходованием средств. На начало страхования (сразу после взноса премии) резерв равен актуар­ной стоимости страховых выплат, которая в свою очередь рав­на величине единовременного взноса Р_х. Если принять, что раз­мер годовой пенсии равен R и она выплачивается в начале го­да, то

о^к*-4г^ж-дГ^Л <¹⁷-²⁴>

Размер резерва в первом периоде (х + t < L)

^NL

Л = -7Г*. (17.25)

С увеличением возраста знаменатель уменьшается и соответ­ственно растет резерв. Во втором периоде (х + t ъ L) динамика резерва иная. Она определяется как

370

Л - "J²* (17.26)

Размеры резерва можно получить и последовательно. Для первого периода он определяется формулой (17.19). Во втором периоде, когда выплачиваются пенсии, получаем

,₊Л = Л*Т--(1+0-Л (17.27)

В свою очередь движение средств на персональном счете (S₍) на каждом шаге во времени рассчитывается в первом периоде как

S,= P_xx(\+/)', (17.28)

а во втором как

5_Ж = 5, х (1 + 0-Л (17.29)

Важно отметить, что поскольку на персональном счете средств меньше, чем сумма резерва, то через некоторый отрезок времени (в возрасте h лет) они полностью исчерпываются (см. рис. 17.5).

ПРИМЕР 17.11. Исходные данные: мужчина, х = 50, L = 60, Я = = 1000 , / = 9%. Размер единовременной премии (коммутацион­ные функции из табл. 12 Приложения):

Мет 3082,2

оЧю - Ъ - дг* ⁼ ТТЙГ^{1000 = 2740}'^2,

Динамика средств на персональном счете и резерва характе­ризуется следующими данными.

x + t	50	55	60	65	00
	2740 2740	4216 4579	6486 7919	4582 7120	1000

Полностью сумма на персональном счете будет исчерпана спустя 10 лет после начала выплат пенсии. Теоретическая нехват­ка средств на индивидуальном счете застрахованного компенси­руется, как и в предыдущем примере, за счет действия принципа солидарности застрахованных.

371

Динамика резерва в рассматриваемом виде страхования раз­личается по периодам. В первом, до начала выплаты пенсии, она описывается формулой (17.23). Что касается второго, то здесь искомая зависимость более сложная. Найдем соотноше­ние двух последовательных показателей резерва:

V N Н-1 Yx _ nx+t+\ V П t ух^jc+z+I	nx+t _ nx+t+\ "x+t "x+t	1 x Px+t
Таким образом,
	"x+t+\

f+l ^rx r x

^Nx+t ^x Px+t

(1 + 0.

(17.30)

Очевидно, что, если второй сомножитель в правой части ра­венства (17.30) меньше множителя наращения (1 +0» то резерв уменьшается с каждым шагом во времени.

ПРИМЕР17.12. Продолжим пример 17.11. Найдем величину ре­зерва для мужчины в возрасте 61 год, применив формулу (17.30):

Чл 2693

11^50 ⁼ lo^so ^х Т; ^х 1.09 = 7919 х———ГТГГГ-х 1,09 =

и 50 ю 50 Л/gQ х р₆₁ 3082 х 0,9692

= 7781, что меньше резерва для 60 лет (см. пример 17.10).