Е. М. Четыркин финансовая математика

• Название: Е. М. Четыркин финансовая математика
• Анкор: chetyrkin_e_m_finansovaya_matematika.doc
• Дата: 22.04.2017
• Размер: 4.63 Mb.
• Имя файла: chetyrkin_e_m_finansovaya_matematika.doc
• Тип: Учебник; #4971
• страница: 25 из 58

§15.3. Модель Блека—Шоулза

Опционы представляют определенный интерес не только в практическом плане, но и в теоретическом — с позиции коли­чественного анализа, который осуществляется с помощью раз­работки специальных моделей (option models), описывающих взаимосвязи основных параметров опционов. Следует, однако,

327

заметить, что теоретические цены опционов, полученные по моделям, в силу неполноты учета экономических условий и их изменчивости, условности входящих статистических данных, как правило, отличаются от рыночных. Вместе с тем, принято считать, что если рыночная цена опциона сильно занижена от­носительно теоретической цены, то есть основание для его по­купки.

Детальное рассмотрение моделей опционов неосуществимо в рамках учебника. Поэтому ограничимся только краткой харак­теристикой наиболее известной из них — модели Блека—Шоул-за (Black—Scholes). Модель Блека—Шоулза разработана в раз­личных модификациях для некоторых видов опционов. Остано­вимся на одной, самой простой модификации, — опцион колл цен обыкновенной акции, при условии, что дивиденды по ак­ции не выплачиваются до дня исполнения.

Выше уже говорилось о том, что цены опционов определя­ются на рынке и зависят от ряда известных и неизвестных на момент его покупки параметров. К основным параметрам мож­но отнести:

• 
  уровень цены исполнения,
  
• 
  текущая цена базового инструмента,
  
• 
  распределение вероятностей рыночной цены базового ин­струмента,
  
• 
  размер процентной ставки,
  
• 
  срок исполнения опциона.
  

Все названные факторы учитываются в формуле Блека—Шо­улза. Для ее записи введем обозначения:

с — цена опциона,

S — текущая цена акции,

Е — цена исполнения,

е⁴** — дисконтный множитель на срок / по непрерывной

ставке б, / — срок до даты исполнения, S — непрерывная процентная ставка (сила роста), принятая

для дисконтирования, N(d_x) и N(d₂) — функции нормального распределения, о²— дисперсия доходности акции (доходность измеряется в

виде ставки непрерывных процентов). Находим

с = S х #Ц) - Е х е^ых N(d₂).(15.3)

328

ПРИМ вестнь года),

rs*

II ф _к ОЙ СЛ

u5io

II s =1

ОЛОЖИ епара 0,09,

°* £ 2

II Ф "

°3 1

1ь Е °

т СП ш

ю II 2

§ Ш1

|"^5

II Э

« " о

т\

«к- - *

g ^ S

I II О

X 2 S

rou ьээ ено

^1з

s °° 2

f?o^

СЛ 1

1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 о — То "ы 4^ "Ln Ъ\ Vj Ъо чо "о — to *u> 4^ Vi Ъ\ "•<* Ьо so	«J
оооооооооооооооооооо _ — —ооооооооооооооооо UiU-SOOOONU»^UWW---000000	N(d)
о о о о о о о о о о о о о о о о о о о о bo^j^^^ul^To^—o^o^-tol^^^^sVibovo	*•
о р о о о о р р о о р р р р о р р о р р 0000Ui-Uivl\O\£)\0OOOOt4)t00^NJ-^ — OvlUi^^OWOOVOO- Гч)^ — Q\ Ui Ы О SO -	N(d)
OO^bNUlVt^NJ^O^boVl^st^V^'rO — OSO	4
p p p p p p p p p p p p p p p p p p p ° ^C ^P ^C ^P ^C -sO vO SO SO SO vp sO vp vO vO vp oo bo oo oo SDSOSOsOsDOOOOOO«g>JO>Ui$U-*0000>^>-N]C\LAW-'SOOSK>N)»*^UUlWSOWA^-*Lft	W)

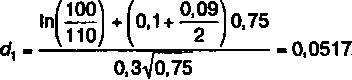
d₂-0,0517-0,3>/0J5 - -0,208.

По таблице плотности нормального распределения находим:

Л/(0,05) = 0,5199,

Л/(-0,2) = 0,4207. Таким образом,

с = 100 х 0,5199 - 110 х е"⁰'¹ * °«⁷⁵ х 0,4207 = 9,06.

При сравнении формул (15.2) и (15.1) легко заметить, что в обеих формулах определяется разность величин S и Е. Однако, в (15.2) эти величины подвергаются взвешиванию, в качестве весов выступают вероятности. Причем N(d₂) можно трактовать как вероятность исполнения опциона на момент истечения срока.

ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА

1. 
   Шарп У.Ф., Александер ГДж,. БейлиДж. В. Инвестиции. Пер. с англ. М: Ин-фра-М, 1997. Гл. 20.
   
2. 
   Браун СДж., Кришмен ММ. и др. Количественные методы финансового ана­лиза. Пер. с англ. М.: Инфра-М, 1996. Гл. 5.
   
3. 
   Хостинге Н., Пикок Дж. Справочник по статистическим распределениям. Пер. с англ. М: Статистика, 1980.
   

Глава 16 СТРАХОВЫЕ АННУИТЕТЫ

§16.1. Финансовая эквивалентность в страховании

В преобладающем числе областей финансовой деятельности объектами приложения методов количественного анализа явля­ются детерминированные процессы, описываемые верными рентами. Однако в страховании и при анализе некоторых инве­стиционных проектов возникает необходимость в использова­нии условных рент (contingent annuity), в которых важную роль играют вероятности наступления соответствующих событий (поступлений или выплат денег). Обсудим методы работы с та­кими рентами, причем для конкретности ограничимся страхо­ванием. Выплата члена ренты в страховании зависит от насту­пления страхового события. Назовем такие ренты страховыми аннуитетами. Заранее число платежей в страховых аннуитетах, а часто и их срок, остаются неизвестными.

Согласно договору страхования страхователь уплачивает впе­ред страховщику некоторую сумму — премию {premium). В свою очередь он (или иной выгодоприобретатель) имеет право полу­чить страховую сумму S после наступления страхового события. Если вероятность наступления этого события q заранее извест­на (на основании прошлого опыта, по аналогии и т.д.), то тео­ретически, без учета всех прочих факторов (в том числе и фак­тора времени), премия Р определяется как

P=Sq.

Приведенное равенство лишь иллюстрирует принцип финан­совой эквивалентности обязательств страхователя и страховщи­ка. Покажем в общем виде, как реализуется этот принцип при расчете страховой нетто-премии, под которой понимается тео­ретическая цена страхования.

331

На практике премия, которая поступает страховой организа­ции, обычно превышает величину нетто-премии, так как вклю­чает помимо нетто-премии и так называемую нагрузку (loading), последняя охватывает все расходы по ведению дела и некото­рую прибыль страховой организации. Определение брутто-пре-мии (нетто-премия плюс нагрузка) является чисто арифметиче­ской задачей, поэтому далее речь пойдет только о нетто-пре­мии.

Пусть Р — размер премии, q_n— вероятность страхового со­бытия (например, смерть застрахованного через п лет после на­чала страхования). Если страховое событие произойдет на пер­вом году страхования, то страховщик получит сумму Р (пусть премия выплачивается в начале года), если же это событие на­ступит во втором году, то сумма премий равна 2Р и т.д. Мате­матическое ожидание такого ряда премий составит:

Pq_{+ 2Pq₂+ ... + nPq_n.

Полученная величина хотя и обобщает все взносы застрахо­ванного с учетом вероятностей их выплат, однако при сумми­ровании соответствующих величин не принимается во внима­ние, что премии выплачиваются в разные моменты времени. С учетом этого фактора (с помощью дисконтирования сумм пла­тежей) находим математическое ожидание современной стои­мости (актуарная стоимость) взносов:

Е(А) = P[q_x+ (1 + v)q₂+ (1 + v + v²)^ + ... +

+ (1 + v + ... + v"-Xb

где v — дисконтный множитель по ставке /.

Обратимся теперь к выплате страховой суммы. Положим, что она выплачивается в конце года, в котором имел место страховой случай. Тогда математическое ожидание выплаты в первом году составит Sq_vво втором году Sq₂и т.д. Математи­ческое ожидание с учетом фактора времени (актуарная стои­мость) выплат, очевидно, можно определить как

E(S) = S(vq_x+ v²^ + ... + V^).

Исходя из принципа эквивалентности обязательств страхов­щика и страхователя, теперь можно написать равенство

332

E(S) = E(A),

которое позволяет найти искомое значение нетто-премии Р. Та­ков в общем виде теоретический подход к методу расчета нет­то-премии, принятый в личном страховании.

Пусть теперь речь идет об имущественном страховании. Если можно полагать, что вероятности наступления страхового случая постоянны, то актуарная стоимость премий за п лет составит

Е(А) = P[q + (1 + v)q + ... + (1 + v + ... + V^^x)q] = PqK,

где К -ai+]?(ai-/)v'.

В свою очередь актуарная стоимость выплат страховых сумм находится как

£(5)-512*

Из равенства актуарных стоимостей взносов и выплат нахо­дим искомый размер нетто-премии.

В практике страховых, или как их часто называют, актуар­ных расчетов разработаны специальные приемы формирования упомянутых выше потоков платежей (страховых аннуитетов) и расчета их актуарных стоимостей.

До обсуждения проблем формирования страховых аннуите­тов, связанных с жизнью людей {life annuity) и их использова­ния для расчетов премий и страховых резервов необходимо оз­накомиться с методикой определения необходимых вероятно­стей и ряда вспомогательных величин, с помощью которых су­щественно упрощается решение соответствующих задач. Речь пойдет о таблицах смертности и коммутационных функциях.

§16.2. Таблицы смертности и страховые вероятности

Таблицы смертности. Для осуществления актуарных расчетов, в том числе расчетов стоимостей страховых аннуитетов, необ­ходимы исходные данные, характеризующие совокупность за­страхованных по полу и возрасту, а также система нормативных демографических показателей, отражающих статистические за-

ззз

кономерности дожития до того или иного возраста. Последние содержатся в таблицах смертности (mortality tables).

Таблица смертности представляет собой числовую модель про­цесса вымирания по возрастам некоторой абстрактной совокуп­ности людей. Такая таблица показывает, как последовательно с увеличением возраста уменьшается эта совокупность, достигая нуля сразу после предельного возраста со. Она является обобще­нием данных демографической статистики за некоторый пери­од времени.

В России таблицы смертности разрабатываются статистиче­скими органами для страны в целом, а также для крупных эконо­мических районов и областей, как для всего, так и отдельно для городского и сельского населения раздельно для каждого пола¹.

Прежде чем приступить к описанию таблицы смертности и актуарных методов анализа необходимо сказать несколько слов о применяемых в актуарных расчетах обозначениях. Актуарная символика в личном страховании сложна, своеобразна и с этим приходится мириться, так как обозначения унифицированы на международном уровне. Одна из отличительных особенностей этой символики — множество нижних и верхних индексов, ко­торые приписываются как справа, так и слева от основной пе­ременной. Например, л , je^i и т.д.

Основной показатель таблицы смертности — число людей 1_Х в возрасте ровно х лет, оставшихся в живых из первоначальной совокупности /₀, обычно равной 100 тыс. человек. Заметим, что и начальный возраст и первоначальное количество людей в таб­лице могут быть любыми — выбор того или иного начального возраста не влияет на результаты актуарных расчетов. Для акту­арных расчетов применяют полные таблицы смертности, в ко­торых возраст показан с интервалом в 1 год.

Величины 1_Х(кроме /₀) определяются расчетным путем на ос­нове заданных вероятностей смерти (q_x), или, что реже, коли­чества умерших (d_x). В современных таблицах смертности ис­ходным показателем обычно служит вероятность смерти, т.е до­ля умерших в возрасте от х до jc -I- 1 лет из числа доживших до возраста х лет. Указанные вероятности получают на основе дан­ных статистики населения с последующим их усреднением и сглаживанием.

¹ Подробные методики разработки таблиц смертности, включая приемы вы­равнивания данных, рассматриваются в курсах демографии. Некоторые перво­начальные сведения по данной проблеме можно получить в "Статистическом словаре". М.: Финансы и статистика, 1989.

334

Помимо показателей 1_Хтаблица смертности содержит число умерших за год в каждой возрастной группе (d_x). Никакие иные факторы выбытия, кроме повозрастных вероятностей умереть, при разработке таблицы во внимание не принимаются.

В качестве иллюстрации приведем фрагмент таблицы смерт­ности для мужчин, в которой начальный возраст — 18 лет¹.

Таблица 16.1 Фрагмент таблицы смертности

лс	'/	Ь	*:
19 20	100 000 99 851 99 678	0,00149 0,00173 0,00196	149 173 195
30	96 991	0,00381	370
35	94 951	0,00487	462
40	92 327	0,00708	654
50	83 640	0,01409	1178
60	68 505	0,02871	1967
70	45 654	0,05691	2598
80	19 760	0,11672	2306

* Округлено до целых чисел.

Показанные в таблице величины 1_Хи d_xсами по себе не име­ют смысла. Они приобретают его лишь при сравнении в рамках таблицы смертности.

Показатели таблицы смертности связаны очевидными соот­ношениями²:

¹ Полная таблица содержится в Приложении (см. табл. 12). Показатели таб­
лицы получены на основе вероятностей q_xиз таблицы смертности населения
СССР за 1984—1985 гг. (журнал "Вестник статистики''. 1987, JSfe 3).

² В таблицах, непосредственно применяемых в страховых расчетах, значе­
ния 1_Хи d_xдля повышения точности расчетов, особенно в старших возрастах,
не округляют до целых чисел.

335


'х+1 'х "х> "х 'х ^х Ч_х\ Ч_х = 1 - Рх = 1 -

Таблица смертности, фрагмент которой приведен выше, яв­ляется минимальной по набору показателей. Она достаточна для простых видов личного страхования — страхования на до­житие и страхования жизни. На практике применяют и более полные таблицы. В частности, в групповом пенсионном и ме­дицинском страховании применяют таблицы выбытия (decre­ment tables), в которых помимо смертности учитываются и дру­гие причины сокращения числа участников страхования.

Страховые вероятности. На основе данных таблицы смертно­сти нетрудно получить систему вероятностей дожития, необхо­димую для расчета соответствующих страховых показателей. Рассмотрим наиболее важные из таких вероятностей.

Вероятность прожить от возраста х до х + п:

пРх = ^Т-06.1)

Вероятность прожить еще один год после возраста х лет:

d_x(c+i

'х 1_Х'

Рх = ^, Чх = ^! - "Т =

ПРИМЕР 16.1. Вероятность мужчине в возрасте 30 лет прожить еще 10 лет составит¹:

/до 92 327 «лРол = — - ***** = 0,95191. ¹°^Рз° /до 96 991 ^u'*⁰¹*'-

По данным таблицы смертности находят и вероятности смерти в определенных возрастах. Например, вероятность уме­реть в возрасте от jc до х + п:

¹ Во всех примерах данного параграфа используется таблица смертности на­селения СССР 1984—1985 гг.

336

Wx-l-^x-^y^-f Ydj.(16.2)

ПРИМЕР 16.2. Вероятность для мужчины в возрасте 30 лет уме­реть в течение 10 следующих лет определяется как

ю^зо ^{= 1} " ю^зо ^{= 1} " 0,95191 = 0,04809.

Вероятность умереть через т лет (на протяжении года т + 1) для лица в возрасте х лет составит:

ХТЩJCt/Я Хт/Пi\C *>\

niflx ⁼тРх ^х Ях+т ⁼Г * 1⁼ Т'⁽ '

х х+т х

В свою очередь вероятность для лица в возрасте х лет уме­реть в возрастном интервале от jc + /и до Jt + m + л лет опреде­лим следующим путем:

	m\rflx	х+т	х+т+п	- =	х+т *х	*х+т	х+т+п х+т
Из	последнего выражения			вытекает,		что
			т\гпх	тгх	х fflx+n	г*

(16.4)

Иначе говоря, искомая вероятность равна произведению ве­роятности дожить до возраста х + т и вероятности умереть в следующие п лет.

ПРИМЕР 16.3. Найдем для мужчины в возрасте 30 лет вероят­ность умереть в течение двух лет после достижения им 33 лет. Находим

_п^Ч^ 95 821-94 951
31^30-—j— geg^ -0,00897.

В некоторых актуарных расчетах (например, в пенсионном страховании) необходимы вероятности дожития супружеских пар. Эти вероятности также рассчитываются по таблицам смертности. Пусть речь идет о супругах в возрасте х и у лет и необходимо оценить вероятности прожить еще п лет для каждо-

337

го из них. Обозначим эти вероятности как _пр_х\ _пр . Определим их следующим образом:

_ ^х+п— у*^п

пРх i ' пРу [ >
ху

где l_x, I — числа доживших до соответствующих возрастов (бе­рутся из таблиц смертности для мужчин и женщин).

В свою очередь вероятности умереть для каждого из супру­гов составят:

rflx nPx⁹ rfly пРу

Рассчитаем еще две вероятности. Однако предварительно примем две рабочие гипотезы:

• 
  оба супруга достигают возрастов хи^в один день;
  
• 
  смерть одного супруга — страховое событие, независимое от смерти другого супруга.
  

Вероятность прожить супругам вместе еще п лет (вероят­ность "сохранения" супружеской пары) рассчитывается как произведение вероятностей двух независимых событий:

(у+я *у+п*х+я ^Х'у+п_/t, <-_ч

пРху⁼_ПРх*пРу = -у-*1=/ _х/ ' ^(1б-⁵⁾

х у х у

В актуарной практике фигурирующие в формуле произве­дения чисел доживших принято обозначать следующим обра­зом:

(к ^Х у *ху ^И (к+я ^х *у+п (яу+я*

Формулу (16.5) теперь можно записать:

ху+п

„Pv = "f• 06.6)

ху

Найдем теперь вероятность того, что супруг (заключивший договор страхования в возрасте х лет, когда его супруге было у лет) не доживет до jc + п лет, а супруга, напротив, доживет до у + п лет. Искомая вероятность (обозначим ее как _пр_х\_у) равна произведению вероятностей:

338

пРЛу - пЯх* пРу- О пР_Х)пРу - пРу - пРх ^х пРу -
У*У

ПРИМЕР 16.4. Пусть возраст супругов 50 и 45 лет. По таблицам смертности находим:

для мужчины /cq = 83640, /« = 77007,

для женщины 1^ = 96261, /^ = 94348.

Вероятность того, что оба супруга проживут следующие 5 лет, составит:

77007 94348

₅Р50;45 = 5%) * 5*>45 = £^ * "эЙбГ ⁼ °*^{92070 Х} °*^{98013 =}

= 0,9024.

Вероятность того, что супруг не проживет 5 лет, а супруга про­живет (см.(16.7)):

505OI45 = И - ₅Р50>5Р45 = О 0.9207) х 0,98013 = 0,007772.