Е. М. Четыркин финансовая математика

• Название: Е. М. Четыркин финансовая математика
• Анкор: chetyrkin_e_m_finansovaya_matematika.doc
• Дата: 22.04.2017
• Размер: 4.63 Mb.
• Имя файла: chetyrkin_e_m_finansovaya_matematika.doc
• Тип: Учебник; #4971
• страница: 21 из 58

§13.2. Схемы погашения задолженности по лизинговому контракту

Количественный анализ лизинговой операции обычно пред­назначен, по крайней мере теоретически, для решения двух за­дач. Для арендатора важно определиться — покупать или арен­довать производственное имущество (если, разумеется, он по своим финансовым возможностям может ставить этот вопрос). Для лизингодателя необходимо определить размер лизинговых платежей и финансовую эффективность сделки.

Назначение лизинговых платежей — полное покрытие издер­жек лизингодателя, связанных с выполнением условий арендно­го контракта, включая расходы по закупке оборудования, креди­тованию и страхованию, а также обеспечение лизингодателю не­которой прибыли и комиссионных. Последние покрывают рас­ходы по подготовке контракта и посреднической деятельности.

Погашение задолженности по лизинговым контрактам мо­жет осуществляться на основе различных схем (способов опла­ты). Лизингополучатель и лизингодатель выбирают и согласо­вывают наиболее удобный для них по срокам и размерам пла­тежей способ.

Задолженность по лизингу погашается следующими видами платежей:

• 
  авансовый платеж,
  
• 
  периодические лизинговые платежи,
  
• 
  выкупная сумма.
  

Основными здесь являются периодические выплаты. Отме­тим лишь несколько признаков, по которым они различаются:

292

• 
  по размеру платежей: постоянные и переменные;
  

• 
  по применяемой процентной ставке: сложная, а иногда (при очень коротких сроках) простая, постоянная или пе­ременная;
  
• 
  по моменту производства платежей: в начале или конце периодов (пренумерандо и постнумерандо);
  
• 
  по периодичности выплат (обычно лизинг предусматрива­ет ежемесячные платежи, редко ежеквартальные или по­лугодовые).
  

Приведенная классификация охватывает большинство из возможных способов погашения задолженности, однако на практике могут иметь место и другие, согласованные участвую­щими сторонами варианты, например, выплаты с удвоенным первым взносом и т.д.

Как правило, финансовый лизинг является средне- или дол­госрочной операцией. Однако в российской практике встреча­ются и краткосрочные, например, на 2 года.

Система основных схем выплат периодических лизинговых платежей представлена на рис. 13.2.

Различие между схемами А и Б платежей заключается в по­следовательности расчетов:

• 
  по схеме А сначала определяется величина лизинговых платежей в целом, далее она распределяется на процент­ные платежи и суммы погашения долга;
  
• 
  по схеме Б сначала рассчитываются размеры процентных платежей и суммы погашения долга (амортизация задол­женности), затем определяется общая величина лизинго­вых платежей.
  

Периодические

платежи

по лизингу

I

Нерегулярные

i

Регулярные

i

Постоянные

С постоянным темпом
изменения

Рис. 13.2

293

Регулярные платежи — лизинговые платежи, производимые через равные интервалы времени в конце или в начале перио­дов. Величина лизинговых платежей не обязательно должна быть постоянной, она может изменяться (увеличение или уменьшение платежей) в ходе погашения задолженности, на­пример, с постоянным темпом.

Нерегулярные платежи — лизинговые платежи, производи­мые по согласованному с лизингодателем графику, содержа­щему суммы платежей и их сроки

Для того чтобы сущность финансового лизинга и влияния условий контракта на размеры платежей были понятны, приве­дем простой пример с последовательными усложнениями усло­вий лизинга. Во всех вариантах стоимость оборудования равна 1000, а срок лизинга составляет 36 месяцев, платежи постнуме-рандо. В вариантах 1—3 предусматривается полное погашение стоимости оборудования, в вариантах 4—5 оборудование выку­пается по остаточной стоимости, равной 200. Соответствующие расчеты приведены в примере 13.1.

Вариант 1. Платежи по 39,23 в конце каждого месяца.

Сумма платежей за весь срок аренды составит 1412,38. Таким образом, общая сумма прибыли лизингодателя за три года рав­на 412,38, или 2% в месяц (24% номинальных процентов в год) от инвестированных средств. Если платежи указанного размера будут вноситься в начале каждого месяца, то это принесет 2,13% в месяц.

Вариант 2. Предусматривается удвоенный взнос в первом периоде и освобождение от взноса в последнем.

При условии, что инвестиции должны принести 2% в месяц, первый взнос должен составить 76,98, остальные — по 38,49.

Вариант 3. Согласно контракту в начале срока лизинга про­изводится авансовый платеж в сумме 100. Аванс 100, остальные платежи по 35,31.

Вариант 4. Арендатор имеет право выкупить имущество в конце срока по цене 200. В этой ситуации — периодические платежи по 35,39 и выкупная цена 200.

Вариант 5. Аванс и право выкупа. Платежи арендатора: аванс 100, платежи по 31,46, выкупная цена 200.

294

§13.3. Методы расчета лизинговых платежей

Для всех лизинговых схем исходным требованием является равенство современной стоимости потока лизинговых платежей затратам на приобретение оборудования, т.е. предусматривается финансовая эквивалентность обязательств обеих сторон конт­ракта. В общем виде требование финансовой эквивалентности обязательств можно записать в виде следующего равенства:

K=PV{R),(13.1)

где К — стоимость имущества для лизингодателя (с учетом та­моженных сборов, страховых расходов и т.д.), PV — оператор определения современной стоимости, Rj — платежи по лизин­гу.

Формула (13.1) конкретизируется с учетом условий лизин­га. В обсуждаемых методиках предполагается, что как при формировании потока платежей, так и при определении сто­имости оборудования в них учитываются все налоговые вы­платы.

Регулярные постоянные платежи, сложные проценты (схема

А). В преобладающем числе случаев поток лизинговых плате­жей представляет собой постоянную ренту. Соответственно ме­тоды расчетов периодических лизинговых платежей базируются на теории постоянных финансовых рент.

Для записи формул примем следующие обозначения:

R — размер постоянного платежа;

п — срок лизинга в месяцах, кварталах, годах (общее число платежей); как правило, в лизинговом контракте число платежей равно числу начислений процентов;

i — процентная ставка за период (норма доходности); если указана годовая номинальная ставка у, то в формулах вместо / используется величина j/m, где т — количество начислений процентов в году;

s — доля остаточной стоимости в первоначальной стоимости оборудования;

a_n;i— коэффициент приведения постоянной ренты постну-мерандо.

295

Если платежи постоянны во времени и погашают всю стои­мость имущества, то, развернув формулу (13.1), получим при выплатах постнумерандо

K=Ra_mP

откуда

Л = . (13.2)

В некоторых схемах для упрощения расчетов размеров пла­тежей во многих случаях можно применить коэффициенты рас­срочки платежей, определяющие долю стоимости оборудова­ния, погашаемую при каждой выплате.

Коэффициент рассрочки для постоянных рент постнумеран­до при условии, что применяются сложные проценты, равен

'■-.-(/и-/)-»- ^<13J)

В свою очередь коэффициент рассрочки для выплат прену-мерандо составит

*2 = 0/%)v, (13.4)

где v — дисконтный множитель по ставке /.

Размеры лизинговых платежей определяются элементарно — путем умножения показателя стоимости имущества на коэффи­циент рассрочки:

Л= Кха_{{2).(13.5)

Значения коэффициентов рассрочки при равных платежах для некоторых сроков лизинга (измеряемых в месяцах и годах) приведены в табл. 10—11 Приложения.

Несколько усложним схему лизинговых платежей. Пусть те­перь первый платеж будет в к раз больше остальных (удвоен или утроен), причем соответственно сокращается число осталь­ных платежей. Тогда условие финансовой эквивалентности обя­зательств удовлетворяется следующими равенствами:

для выплат постнумерандо

К={к- l)*v+&*„_*+!;/ 296

и для платежей пренумерандо

*=<*-1)Л+Л^1;/<¹⁺0.

На основе этих равенств легко найти необходимые значения лизинговых платежей, а именно:

^{Л =} Т—ГТ /, ■ ч- О³-⁷)

*-1 + *„-*+!;/О +0

Теперь примем во внимание выплату аванса (обозначим его как А). Для лизинговых платежей постнумерандо и пренумеран­до соответственно получим следующие уравнения эквивалент­ности:

К=А + Ra_ni9K=A+ Ra_n;i(l + /).

Для расчета R применим коэффициенты рассрочки. После чего

R=(K-A)a_H2).(13.8)

Если лизинговый контракт предусматривает выкуп имущест­ва по остаточной стоимости, доля которой в стоимости имуще­ства равна 5, то уравнение эквивалентности при платежах пост­нумерандо имеет вид

К= Ra_n;i+ Ksvⁿ, откуда

R « —* ^L- К{\ - svⁿ)a_v(13.9)

^an;i

Аналогично для платежей пренумерандо получим К(\ — svⁿ)

*=ТаГГо"«¹-"•>'>■ <^шо>

Закончим обсуждение метода расчета суммы платежа вари­антом, в котором одновременно учитывается авансовый платеж

297

и выкуп имущества. В этом случае для последовательностей платежей постнумерандо и пренумерандо имеем

К(1 - sv") = А + Ra_nj, К(\ - sv") = А + Яа_я1(1 + /).

Соответственно, получим

„ [АГ(1 - sv") - А]

R = -^L-^{1 L},(13.11)

„ [K(l - sv") - А]

" s.o + 0 • ^(l3,2>

ПРИМЕР 13.1. В §13.2 приведены различные варианты условий лизинга. Рассчитаем для них значения лизинговых платежей, ис­пользуя приведенные выше формулы.

Общие исходные данные: К= 1000, п= 36 месяцев, / = 2% в месяц, выплаты постнумерандо.

Вариант 1. Находим по (13.3) коэффициент рассрочки (плате­жи в конце периодов) и затем размер ежемесячного платежа

а₁ ш ₁ .У^-зб = 0,03923; Я = 1000 х 0,03923 = 39,23.

Если платежи вносятся в начале каждого месяца, то согласно (13.4)

а₂ = 0,039233 х1,02"¹ = 0,038464 и R = 38,46.

Вариант 2. Удвоенный взнос в первом месяце (к - 2). Для взносов в конце периодов получим по (13.6)

1000
Я = _{Qr1 +а} = 38,49 и первый взнос 2Я = 76,98.

Вариант3. А= 100. На основе (13.8) находим

Я = 900x0,03923 = 35,31.

Вариант 4. В этом варианте $ = 0,2. Таким образом, Ks'= = 1000 х0,2 = 200 и согласно (13.9) получим

Я = 1000(1 - 0,2 х 1,02"³⁶) х 0,03923 = 35,39.

298

Вариант 5. А= 100, s = 0,2. По формуле (13.11) находим R = [1000 х (1 - 0,2 х 1.02-³⁶) - 100] х 0,03923 = 31,46.

Перейдем ко второй задаче — делению суммы платежа по лизингу (R) на сумму амортизации долга и выплату процентов. Сумма, идущая на погашение основного долга, находится как разность лизингового платежа и процентов на остаток задол­женности.

1. Платежи постнумерандо

d_t= R- Z)_M x/, /= 1,...,л, (13.13)

где d_t— сумма погашения основного долга в периоде /, D_t__x— остаток долга на конец периода / — 1, D₀= К.

В первом периоде

d_{ = R- KL

Остаток задолженности последовательно определяется как

D_t=D,__x-d_r(13.14)

2. Платежи пренумерандо

4 = Л,
d₂= R- Ki,
d_t= R--Z)_Mi. (13.15)

ПРИМЕР 13.2. К = 100, п - 5 лет, / = 10% годовых, платежи в конце периодов, полное погашение стоимости оборудования (s = = 0). По формуле (13.2) получим

* = ¹⁰° * ₁ .₍Д¹₀₁₎-5 = ¹⁰° * °»²⁶³⁸ = ²⁶»³⁸-

(Табличное значение коэффициента рассрочки равно 0,263797 (см. табл. 11 Приложения).)

Если контракт предусматривает платежи в начале каждого го­да, то коэффициент рассрочки определим по (13.4):

299

^я - ^iooi-(i°;¹o,i)-s* tttw - ^1о°* °-²³⁹⁸² -^2з-⁹⁸²-

Проценты за первый год 100 х 0,1 = 10, сумма погашения дол­га 26,38 - 10 = 16,38. График погашения задолженности при вы­платах постнумерандо приведен в табл. 13.1.

Таблица 13.1

t	Остаток долга	%	Погашение	Лизинговые
	на конец периода		долга	платежи
1	100,000	10.000	16,380	26,38
2	83,620	8,362	18,018	26,38
3	65,602	6,560	19,820	26,38
4	45,782	4,578	21,802	26,38
5	23,980	2,398	23,980	26,38

Как видно из таблицы, суммы, предназначенные для погаше­ния основного долга, увеличиваются, в то время как процентные платежи сокращаются.

Если в условиях данного примера предусматривается остаточ­ная стоимость в размере 10% от первоначальной стоимости обо­рудования {$ = 0,1), то размер лизингового платежа (выплаты по­стнумерандо) составит согласно (13.9)

Я = 100(1 - 0,1 х1,1-5) х0,2638 = 24,742.

График выплат представлен в табл. 13.2.

Таблица 13.2

t	Остаток долга	%	Погашение	Лизинговые
	на конец периода		долга	платежи
1	100,000	10,000	14,742	24,742
2	85,258	8,526	16,215	24,742
3	69,043	6,904	17,837	24,742
4	51,205	5,121	19,621	24,742
5	31.584	3,158	21,584	24,742

Проверка: остаточная стоимость 3>,584 - 21,584 = 10,000.

Размер платежа по лизингу зависит от ряда параметров, часть из которых определяется в ходе разработки лизингового контракта. Такие величины, как срок и процентная ставка,

300

можно рассматривать как управляющие параметры, поскольку, изменяя их размер, достигают необходимого компромисса, удо­влетворяющего участвующие стороны. В связи со сказанным, проследим влияние указанных параметров на величину коэф­фициента рассрочки.

Очевидно, что с увеличением срока коэффициент рассрочки уменьшается. В пределе при п -*» получим а_х= /(см. рис. 13.3).

Как видим, увеличение срока лизинга заметно сказывается в начале шкалы сроков и уменьшается при больших сроках. Ска­занное иллюстрируется следующими данными, подсчитанными для / = 5%:

п	4	8	16	20
а	0,28201	0,15472	0,09227	0,08024

0,05

Что касается процентной ставки, то очевидно, — чем она выше, тем больше коэффициент рассрочки, причем при / =* 0 имеем а_х= \/п (см. рис. 13.4). Влияние ставки усиливается вме­сте с ростом размера ставки. Так, для п = 12 находим следую­щие результаты:

0,08333

5 0,11283

10 0,14676

15 0,18448

Если имущество куплено за собственные средства лизинго­дателя, то процентная ставка / характеризует доходность от их инвестиций. Если имущество полностью приобретено за счет привлеченных средств, причем за кредит выплачиваются про­центы по ставке г, то доходность от предпринимательской дея­тельности лизингодателя составит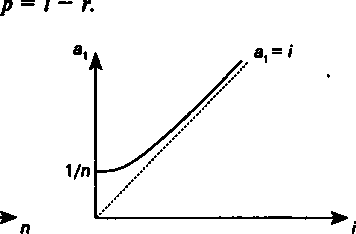

Рис* 13.3

Рис. 13.4

301

Таким образом, обязательным условием операции является /> г.

Два слова о влиянии остаточной стоимости. При заданных размерах процентной ставки и срока лизинга увеличение доли остаточной стоимости линейно уменьшает величину коэффи­циента рассрочки.

Регулярные постоянные платежи (схема Б). Исходное требо­вание: величина платежа определяется размером сумм погаше­ния основного долга и выплат процентов. Расчет выполняется по схеме погашение задолженности равными долями (суммами) (си. § 9.3). Для схемы с полным погашением стоимости

_J К

d= — = const. п

Платежи по лизингу в конце периода t находятся как

Л,= />_м х /+
где R_t— размер лизингового платежа в периоде t

Остаток долга на конец периода последовательно находится как разность

/>,= />_М-Л (13.17)

ПРИМЕР 13.3. Исходные данные: К= 100, л = 5, / = 10%, плате­жи постнумерандо. Основной долг погашается полностью равны­ми суммами (см. табл. 13.3).

Таблица 13.3

t	Остаток долга	%	Погашение	Лизинговые
	на конец периода		долга	платежи
1	100	10	20	30
2	80	8	20	28
3	60	6	20	26
4	40	4	20	24
5	20	2	20	22

Как видим, этот вариант погашения задолженности отличает­ся более крупными платежами в начале действия контракта.

302

Нерегулярные платежи (схема А). Задается график лизинго­вых платежей (сроки и суммы). Сбалансированность выплат и задолженности достигается при определении размера последней выплаты. Исходное равенство

где R_v n_t— сумма и срок /-го платежа, R_k, n_k— сумма и срок последнего платежа.

Деление суммы платежа на проценты за кредит и суммы, по­гашающие основной долг, производится последовательно по формуле

4-4-Ям*'-

ПРИМЕР 13.4. К= 100, л = 5, / = 10%, платежи постнумерандо. Задан график четырех последовательных выплат (см табл. 13.4). 4 Сумма дисконтированных платежей равна УЯ,у"'-96,242. Размер последнего платежа: Я5 = (100 - 96,242) / v5 = 6,054. Таблица 13.4
t	Срок	Лизинговые платежи	Остаток долга на конец периода	%	Погашение I долга
1 2 3 4 5	0.5 1.0 2.0 2.5 5.0	50 40 10 5 6.054	100.000 54,881 17,560 9,316 4,771	4,881 2,019 1,756 0,455 1,283	45.119 37.321 8.224 4.545 4.771
		111.054			100.0

Нерегулярные платежи (схема Б). Задается график погашения основного долга. Проценты за кредит последовательно начис­ляются на остаток задолженности.

ПРИМЕР 13.5. К= 100, п= 5, / = 10%, $ = 0, платежи в конце года. Расчет лизинговых платежей см в табл. 13.5.

303

Таблица 13.5

t	Погашение	Остаток долга	%	Лизинговые
	долга	на конец года		платежи
1	10	100	10	20
2	30	90	9	39
3	30	60	6	36
4	20	30	3	23
5	10	10	1	11
	100	—	29	129

ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА

1. 
   Четыркин Е.М. Финансовый анализ производственных инвестиций. М.: Де­ло, 1999. § 7.3.
   
2. 
   Четыркин Е.М. Методы финансовых и коммерческих расчетов. М.: Дело, 1995. §12.5.
   
3. 
   Leasing Finance. 2-ed. Euromoney Books, 1990.
   

Глава 14 ФОРФЕЙТНАЯ ОПЕРАЦИЯ