Е. М. Четыркин финансовая математика

• Название: Е. М. Четыркин финансовая математика
• Анкор: chetyrkin_e_m_finansovaya_matematika.doc
• Дата: 22.04.2017
• Размер: 4.63 Mb.
• Имя файла: chetyrkin_e_m_finansovaya_matematika.doc
• Тип: Учебник; #4971
• страница: 19 из 58

§12.5. Срок окупаемости

Срок окупаемости, как уже отмечено выше, определяется в двух вариантах — на основе дисконтированных членов потока платежей и без дисконтирования. Обозначим первый как я_ок, второй как т. Величина п_окхарактеризует число лет, которое необходимо для того, чтобы сумма дисконтированных на мо­мент окончания инвестиций чистых доходов была равна разме­ру инвестиций (барьерная точка для срока). Иначе говоря, это расчетное время, необходимое для полной компенсации инве­стиций поступающими доходами с дисконтированием обоих потоков по ставке приведения. Второй показатель в общем смысле аналогичен первому, но время получения доходов не учитывается и доходы не дисконтируются.

В предельно простом случае срок окупаемости т определя­ется как отношение суммы инвестиций к средней ожидаемой величине поступаемых доходов:

К т =

Такой расчет, очевидно, имеет смысл при относительно не­значительных колебаниях годовых доходов относительно сред­ней. В финансовом отношении более обоснованным является дисконтный срок окупаемости м_ок.

Пусть размеры капитальных вложений к концу срока инве­стирования составляют величину К. Доходы поступают в виде

273

нерегулярного потока платежей R_rНеобходимо найти такой срок, при котором будет выполнено равенство

£/?/ - К.(12.13)

/-I

ПРИМЕР 12.6. Найдем сроки окупаемости (величины ти л_ок) для потока платежей примера 12.1 (вариант Л). Напомним, что поток состоит из следующих членов: -100; -150; 50; 150; 200; 200. Об­щая сумма капитальных вложений равна 250. Суммируем доходы за первые два и часть третьего года и приравняем полученную сумму к размеру инвестиций:

50+ 150 + 200х = 250,

где х— доля годового дохода.

Отсюда х= 50 : 200 = 0,25 и т= 2 + 0,25 = 2,25. Для вари­анта Бтого же примера получим т= 3,5 года.

Для определения дисконтного срока окупаемости установим размер ставки приведения: / = 10%. Сумма капиталовложений с наращенными процентами к концу второго года равна 260. Сов­ременная стоимость поступлений за первые два года, рассчитан­ная на момент начала отдачи, составит 169,4 для варианта А, т.е. меньше 260, а за три года поступлений — 319,7, т.е. больше этой суммы. Отсюда срок окупаемости примерно равен

л^ = 2 + (260 - 169,4) : (200 х 1,1"³) = 2,6 года после завер­шения инвестиций. Для варианта Бнаходим п - 4.

Остановимся на ситуации, когда капиталовложения заданы одной суммой, а поток доходов постоянен и дискретен (посто­янная ограниченная рента). Тогда из условия полной окупаемо­сти за срок п_окпри заданной процентной ставке / и ежегодных поступлений постнумерандо следует:

l-fw/p

К -Л—1 1 .

/

Отсюда

1п(1 + /)

(12.14)

274

ПРИМЕР 12.7. Определим дисконтный срок окупаемости для данных примера 12.5 при условии, что поступления дохода про­исходят: 1) равномерно в пределах года, 2) раз в конце года. Ди­сконтирование осуществим по ставке 10%.

1. Припишем суммы годовых доходов к серединам годовых ин­тервалов. После чего применим формулу (12.14) с небольшим уточнением, вызванным тем, что выплаты производятся не в кон­це каждого года, а в середине:

-^|п(¹ - я(ТТ»Г^/)

^п°* 1п(1 + I)

_-^,п₍¹ _-^п^Н

2. По (12.14) находим: п_ок = 8,89 года.

Для сравнения заметим, что без учета времени поступления доходов срок окупаемости составит всего т= 5,71 года.

Заметим, что дисконтный срок окупаемости существует, ес­ли не нарушаются определенные соотношения между доходами и размером инвестиций, а именно: если постоянные доходы по­ступают ежегодно, то R > НС. Это вытекает из формулы (12.14). Можно получить аналогичные по содержанию соотношения и для других видов регулярных потоков дохода. Так, при поступ­лении доходов в виде /ьсрочной ренты соотношение имеет вид R > р[(\ + i)V^p— 1]AT; аналогично при непрерывном поступле­нии доходов R > 1п(1 + i)K или R > 6К.

Приведенные неравенства, вероятно, окажутся полезными для быстрой оценки сложившейся ситуации. Если указанные требования не выполняются, то инвестиции при принятом уровне процентной ставки не окупаются. В то же время срок окупаемости, подсчитанный без учета фактора времени, в лю­бом случае будет иметь некоторое положительное значение.

ПРИМЕР 12.8. Пусть сделаны разовые инвестиции К= 4, ожида­емая постоянная годовая отдача равна 0,2. Если / = 10%, то име­ем R = 0,2 < 0,1 х 4. Таким образом, при заданном уровне посту­плений и принятой ставке приведения условие окупаемости не выполняется. Однако упрощенный способ определения срока оку­паемости говорит об обратном: т = 4/0,2 = 20 лет.

275

Влияние факторов и взаимосвязь сроков окупаемости. На ве­личину дисконтного срока окупаемости влияют два фактора — распределение поступлений во времени ("профиль" доходов) и ставка, принятая для дисконтирования (ставка приведения). Влияние первого фактора очевидно — концентрация отдач к концу срока проекта, да и вообще любая отсрочка поступлений доходов увеличивает срок окупаемости. Что касается второго фактора, то его влияние столь же понятно — с увеличением ставки приведения срок окупаемости растет.

Коль скоро оба рассмотренных срока окупаемости характе­ризуют одно и тоже свойство инвестиционного процесса, то ме­жду ними, очевидно, должна существовать некоторая зависи­мость, которая в значительной мере определяется видом рас­пределения доходов во времени. Аналитически можно просле­дить эту зависимость для случая с поступлениями дохода в ви­де постоянной дискретной ренты. Определим оба показателя срока окупаемости через размер инвестиций и постоянные еже­годные поступления:

К

R " I

Откуда следует, что

_ -ln(l - mi) ^П°^к" 1п(1 + /)

(12.15)

При mi > 1 инвестиции не окупаются. Графическая иллюст­рация зависимости двух видов сроков окупаемости от отноше­ния K/R представлена на рис. 12.7.

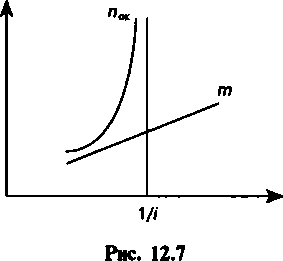
Л7, П₀

K/R

276

§12.6. Индекс доходности

Рентабельность инвестиций также может быть измерена дву­мя способами: бухгалтерским и с учетом фактора времени (с дисконтированием членов потока платежей). В обоих случаях доход сопоставляется с размером инвестиций. На основе бух­галтерского метода получим два варианта индекса доходности:

2я. 2/?.-* 2л.

j j j

и = —— или и = - = —z 1.

В последней записи этот индекс совпадает с принятым у нас показателем рентабельности.

Интересно проследить влияние взаимозависимости бухгал­терских срока окупаемости и показателя рентабельности. Для этого обратимся к случаю, когда доходы постоянны во време­ни. Упомянутые показатели определяются на основе следую­щих равенств:

К Rn

^{т =} 7^{им =} Т"

Таким образом,

п и = —. т

Рентабельность и срок окупаемости находятся, как видим, в обратной зависимости.

При дисконтировании членов потока платежей индекс до­ходности определяется следующим образом: если капиталовло­жения приведены к одной сумме К, то

2/?_yv

# = ^у-. (12.16)

Если же капитальные затраты распределены во времени, то имеем

J ^RJ^yJ+ni
U^J . (12.17)

277

ПРИМЕР 12.9. По данным примера 12.1 приведенные к началу срока инвестиционного проекта капиталовложения для варианта А составили 214,9, доход 377,1, а для варианта Б соответственно 223,1 и 386,2. На основе этих данных получим следующие пока­затели рентабельности:

377,1 386,2

Если поток доходов представляет собой постоянную ренту постнумерандо, а капиталовложения мгновенны, то

"=-£*„;,. (12.18)

ПРИМЕР 12.10. Поток доходов и остальные условия инвестиро­вания показаны в примере 12.5. Определим индекс доходности в случае, когда дисконтирование производится по ставке 10%:

0,7 U--t"*io;io-1-183.

Аналогичным путем можно определить рентабельность и для иных видов распределения доходов во времени.

§12.7. Соотношения относительных измерителей эффективности

Относительные финансовые показатели эффективности ин­вестиций, на которых мы останавливались выше, имеют сход­ную задачу и базируются, в конечном счете, на одной методи­ке — сопоставлении доходов и затрат. Однако каждый из них решает задачу под своим углом зрения. Можно ожидать, что подобные измерители взаимосвязаны, причем в общем дина­мика одного показателя не пропорциональна изменению дру­гого. Знакомство с некоторыми из таких зависимостей, вероят­но, окажется полезным для лучшего понимания существа рас­смотренных показателей и их применения в практических си­туациях.

Зависимости между попарно взятыми показателями эффек­тивности легко выявить аналитическим путем для случаев, ко­гда поток доходов может быть представлен в виде дискретной

278

финансовой ренты, а капиталовложения мгновенны. Ограни­чимся только двумя наиболее интересными соотношениями. Начнем с взаимосвязи чистого приведенного дохода и внутрен­ней нормы доходности. На основе формул (12.1) и (12.2) нахо­дим следующую зависимость:

N=R(a_n;i-a_n.J).

Здесь / — ставка, которая применяется при определении чисто­го приведенного дохода N. Как видим, величина N оказывается положительной, если / < У. Графическая иллюстрация данной зависимости представлена на рис. 12.8.

Зависимость внутренней нормы доходности и дисконтиро­ванного срока окупаемости определяется следующим образом¹:

_{-4-7 ['-Mil}

"-— ifrnj—•

(12.19)

График этой зависимости представлен на рис. 12.9.

Приведенные выше соотношения, напомним, получены для частного случая, когда капиталовложения мгновенны, а отдача от них представляет собой ограниченную постоянную ренту по-стнумерандо. В действительности поток доходов далеко не все­гда следует указанной закономерности. В силу этого наблюда­ются отклонения от найденных соотношений.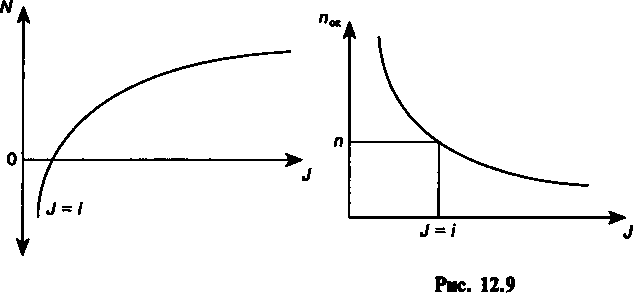

Рис. 12.8







¹ См. Математическое приложение к главе.

279

§12.8. Сравнение результатов оценки эффективности

Применяемые при сравнении нескольких инвестиционных проектов показатели могут и часто дают разные результаты по их предпочтительности. Нельзя забывать и то, что дисконтные показатели эффективности (кроме J) зависят от принятой в расчетах процентной ставки. Неоднозначность результатов объ­ясняет, почему многие инвесторы для повышения надежности выбора применяют несколько критериев. Для того чтобы ска­занное было более наглядным, приведем следующую иллюстра­цию. Сравним по шести критериям шесть проектов (см. табл. 12.3). В таблице выделены наиболее привлекательные варианты по каждому из критериев. Два первых проекта одинаковы по общей сумме капиталовложений и отдач, но их распределения во времени имеют существенные различия. Проект В отличает­ся от Б только тремя дополнительными годами поступления до­хода. Аналогичное с вариантом Б распределение поступлений и у варианта Д. Однако, начало поступлений дохода здесь запаз­дывает на один год. Наконец, вариант Г отличается от Б тем, что на восьмом году реализации проекта предусматривается мо­дернизация производства (в связи с этим текущие расходы пре­вышают доходы) с последующим увеличением срока поступле­ний дохода.

Перейдем к результатам оценивания эффективности данных вариантов. Соответствующие показатели приведены в нижних строках табл. 12.3. Сравним варианты А и Б. По всем критери­ям за исключением и первый вариант предпочтительней второ­го. Объясняется это только различием распределений во време­ни как капиталовложений, так и доходов. При сравнении вари­антов Б и В находим, что продление срока поступлений улуч­шает все показатели, кроме сроков окупаемости — на них до­полнительные годы отдачи не отражаются. В свою очередь ва­риант Д отличается заметным ухудшением всех показателей (кроме и), что объясняется запаздыванием поступлений доходов всего лишь на один год. У этого варианта самая низкая внут­ренняя норма доходности. Вариант Г, отличающийся от В наи­большим сроком поступлений и их объемом, имеет лучший по­казатель чистого приведенного дохода, но не внутренней нор­мы доходности.

280

Таблица 12.3

t	1 A 1	Б	В	Г	Д
1	-100	-200	-200	-200	-200
2	-150	-50	-50	-50	-50
3	50	50	50	50	0
4	150	100	100	100	50
5	200	100	100	100	100
6	200	200	200	200	100
7	50	200	200	200	200
8			100	-150	200
9			100	150	100
10			100	150	100
11				150	100
12				150
13				100
14				100
15				100
2*	-250	-250	-250	-400	-250
Xr	650	650	950	1150	950
m	2,25	3,0	3,0	4,0	4,0
и	2,6	2,6	3,8	2,9	3,8
N	187,9	160,3	288,0	391,4	241,5
J	32,9	25,3	30,5	30,5	24,5
"ok	2,6	4,0	4,0	5,1	4,0
и	1,87	1,72	2,29	2,09	1,91