Е. М. Четыркин финансовая математика
 Скачать 4.63 Mb.
|
§11.2. Измерение доходности облигацийу/ i = ( g НИМ' ( i,V  ПРИМЕР 11.1. Вечная рента, приносящая 4,5% дохода, куплена по курсу 90. Какова финансовая эффективность инвестиции при условии, что проценты выплачиваются раз в году, поквартально (Р = 4)?( 0,05 У = 0,05; / = 1 +-^Ч - 1 =0,С 0,045 / = /f = -^—100 = 0,05; / = |1+^т=-| -1=0,0509. Облигации без выплаты процентов. Данный вид облигации обеспечивает ее владельцу в качестве дохода разность между номиналом и ценой приобретения. Курс такой облигации всегда меньше 100. Для определения ставки помещения приравняем современную стоимость номинала цене приобретения: ж, РК Nvn= " или Vя = — = лгу р или v N10(), где п — срок до выкупа облигации. После чего получим 1 '(П.4) ПРИМЕР 11.2. Корпорация X выпустила облигации с нулевым купоном с погашением через 5 лет. Курс реализации 45. Доходность облигации на дату погашения /•-4— -1-0,1731$ V100 т.е. облигация обеспечивает инвестору 17,316% годового дохода. Облигации с выплатой процентов и номинала в конце срока. Проценты здесь начисляются за весь срок и выплачиваются одной суммой (lump sum) вместе с номиналом. Купонного дохода 235 Из последней формулы следует /-ilL-i. (11.5) "'100 10( Если курс облигации меньше 100, то / > g.  ПРИМЕР 11.3. Облигация, приносящая 10% годовых относительно номинала, куплена по курсу 65, срок до погашения 3 года. Если номинал и проценты выплачиваются в конце срока, то полная доходность для инвестора составит«0,26956, или 26,956%. Облигации с периодической выплатой процентов и погашением номинала в конце срока. Этот вид облигаций получил наибольшее распространение в современной практике. Для такой облигации можно получить все три показателя доходности — купонную, текущую и полную. Текущая доходность рассчитывается по полученной выше формуле (11.2). Что касается полной доходности, то для ее определения необходимо современную стоимость всех поступлений приравнять цене облигации. Поскольку поступления по купонам представляют собой постоянную ренту постну-мерандо, то член такой ренты равен gN9а современная ее стоимость составит gNan.nесли купоны оплачиваются ежегодно, и gN(№.rесли эти выплаты поизводятся р раз в году, каждый раз по ставке g/p. Дисконтированная величина номинала равна Nvn. В итогб получим следующие равенства. Для облигации с годовыми купонами Р « Nvn +gN^v* « Nvn+ gNan.h(11.6) l 236 In /2 / « gN+(C-P)l n (C + P) /1 8\N 100 N 100 (11.14) Ставка помещения для серийных облигаций. Общий принцип определения полной доходности и в этом случае не изменяется: рыночная цена приравнивается к сумме членов потока платежей, дисконтированных по неизвестной ставке помещения. Однако число этих членов меняется от серии к серии. В связи со сказанным в расчет обычно берется то число членов потока, которое находится в интервале от начала до среднего ее срока, метод расчета последнего рассмотрен в § 11.4 (см. (11.19)). Сравнение показателей доходности облигаций. Нетрудно установить, что соотношения между характеристиками доходности зависят от курса облигации. Так, для облигаций, у которых К < < 100, находим g < it < i < /', и наоборот, если К > 100, то g > > /, > / > Г. Наконец, если курс равен 100, то все показатели доходности равны купонному доходу при ежегодной его выплате. Динамика показателей доходности в зависимости от курса показана на рис. 11.1 Доходность к 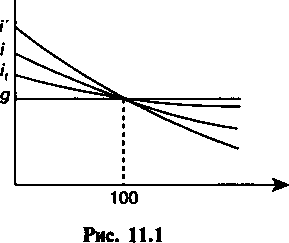 КурсДоходность облигаций с учетом налогов. До сих пор мы не принимали во внимание налоги на доходы, которые приносят облигации. Отсутствие развитого пакета законов о налогообложении доходов от ценных бумаг не позволяет при обсуждении этой проблемы исходить из отечественной практики. Во многих странах ставки налога на доход дифференцированы по видам 240
Существует метод, который позволяет приближенно оценить полную доходность с учетом налоговых выплат, если известна ставка помещения без учета налогов: У-*(!-/) +('-*)(!-«). (И.17) ПРИМЕР 11.6. Для данных примера 11.5 получим у- 8(1 - 0,2) + (19,62 - 8)(1 - 0,28) = 14,77%. Напомним, что точное значение равно 15,53%. Все приведенные здесь расчеты предполагали, что уплата налогов по времени совпадает с получением доходов по облигации. Отсрочка в выплате налогов, естественно, увеличивает ставку помещения. §11.4. Характеристики сроков поступлений средств и измерение риска Для обоснованного выбора облигации недостаточно располагать данными об их доходности. Необходимо как-то оценить и риск. Последний, очевидно, связан со сроком облигации — чем больше срок, тем выше риск. Однако непосредственное сравнение сроков не приведет к правильным выводам, посколь- 242 ку при этом не учитываются особенности распределения доходов во времени ("профиль" поступлений доходов). Ясно, что облигации с нулевым купоном более рискованны, чем облигации с периодическим выплатами процентов при одном и том же их сроке, так как все поступления происходят в конце срока. Для характеристики облигаций под этим углом зрения применяют два вида средних сроков платежей. Обе средних являются взвешенными арифметическими. Отличие — в методе взвешивания. Назовем первую среднюю средним арифметическим сроком (average life), вторую, для того чтобы отличить от первой, назовем средним сроком дисконтированных платежей (duration). Рассмотрим обе средние. Средний арифметический срок. Этот показатель обобщает сроки всех видов выплат по облигации в виде средней взвешенной арифметической величины. В качестве весов берутся размеры выплат. Иначе говоря, чем больше сумма выплаты, тем большее влияние на среднюю оказывает соответствующий срок. Для облигаций с ежегодной оплатой купонов и погашением номинала в конце срока получим 1>ф. gNlttj+nN Г'^Г° j ' где Т — средний срок, t — сроки платежей по купонам в годах, Sj — сумма платежа, g — купонная норма процента, л — общий срок облигации. Известно, что для t,= 1,2, ..., п Г' 2 ' поэтому вместо (11.18) можно применить *(* + О , j Г= Очевидно, что Т<п.Уоблигаций с нулевым купоном Т = п. Нетрудно понять, что чем больше купонный процент, тем меньше средний срок. 243  ПРИМЕР 11.7. Найдем средний арифметический срок для двух облигаций с выплатами по купонам 5 и 10% от номинала, срок облигаций 10 лет. По формуле (11.19) получим0,05 х 11 t 1 0,1 х 11 t 1 г1=—5js—=8'5: т* =—м— = 7'75г°да- Пусть теперь купоны оплачиваются р раз в году, например, по полугодиям или ежеквартально, тогда необходимая нам сумма сроков платежей находится как у пр(п + 1 / р) Теперь вместо (11.19) имеем !<я+1//»+1 Т= — . (11.20) g+ 1 / п Очевидно, что переход от годовой выплаты процентов к выплатам по полугодиям или по кварталам несколько снижает средний арифметический срок облигации. Чем меньше средний арифметический срок, тем скорее получает отдачу от облигации ее владелец и, следовательно, меньше риск. Несколько слов о содержании полученной средней. Предварительно вспомним понятие "кредитная услуга", под которой обычно понимают произведение суммы кредита на срок ("руб-ле-годы"). В числителе формулы (11.18) показан полный размер кредитной услуги по облигации — все ожидаемые поступления умножены на соответствующие сроки. Средний арифметический срок указывает на момент в сроке облигации, который уравнивает размеры кредитных услуг в том смысле, что сумма кредитной услуги до среднего срока равна кредитной услуге после этого момента: ЯМ-*'**»<»-21> где Ау, гк — временные интервалы от даты платежа до среднего срока (/ — платежи, производимые до среднего срока, к — после этого срока). 244 Для иллюстрации обратимся к облигации из примера 11.4 со сроком 5 лет. Ее средний срок равен 4,43 года. Размер кредитной услуги на эту дату равен примерно 62. Кредитная услуга для оставшегося срока равна такой же величине. Механический аналог среднего срока — точка равновесия платежей во времени. Средний срок дисконтированных платежей. Обсуждаемый показатель также представляет собой среднюю взвешенную величину срока платежей, однако взвешивание здесь более "тонкое", учитывающее временную ценность денег. В качестве такого показателя, который, кстати, вытесняет в современной практике средний арифметический срок, применяют так называемый средний срок дисконтированных платежей. Обозначим эту величину как D. Пусть проценты выплачиваются ежегодно, тогда имеем (11.22) Знаменатель формулы по определению равен рыночной цене облигации (см. (11.6)). После ряда преобразований получим gyt,vJ+v" D-Z^ ,/,= 1,2,...,/!. (11.23) АГ/100 Jv ' Дисконтирование здесь производится по ставке помещения.
245 Находим 268 D = -£jj- = 4,12 года. Напомним, что средний арифметический срок для этой облигации равен 4,43 года. Очевидно, что для облигации с нулевым купоном D = Т = п. В остальных случаях D < Т < л. На рис. 11.2 иллюстрируется зависимость среднего взвешенного срока платежей от общего ее срока (/ — облигации с нулевым купоном, 2 — купленные по номиналу, 3 — купленные с дисконтом, 4 — купленные с премией; по облигациям вида 2—4 предусматривается выплата купонного дохода). Рассматриваемый показатель увеличивается при сокращении купонного дохода, а также с падением средней ставки на рынке и ростом общего срока. Из определения D и приведенных формул следует, что этот показатель учитывает особенности потока платежей — отдаленные платежи имеют меньший вес, чем более близкие к моменту оценки. Заметим, что эту величину можно трактовать и как срок эквивалентной облигации с нулевым купоном. °t ' X 2 у/у^ 3 >^O^^Z- 4 Рис. 11.2 В примере 11.8 средний срок платежей по облигации составил 4,12 года. Это означает, что она эквивалентна займу без текущей выплаты процентов с аналогичной нормой доходности (19,62%) при условии, что его срок равен 4,12 года. Модифицированный средний срок дисконтированных платежей. Средний срок дисконтированных платежей, о котором 246  только что шла речь, едва бы привлек внимание финансистов-аналитиков, будь он только обобщенным измерителем срока платежей. Ценность этого показателя состоит в том, что его можно использовать как меру чувствительности цены облигации к незначительной динамике уровня процентной ставки на рынке. Для решения этой задачи, строго говоря, применяется не величина Д а ее модификация, обозначим ее как MD {modified duration), которую для краткости назовем модифицированная средняя. Этот показатель часто называют средней Макколея:MD = —^-T,(11.24) 1 + -Р где / — полная доходность облигации, р — количество выплат процентов в году. Можно доказать, что MD представляет собой показатель эластичности цены облигации по рыночной процентной ставке. Иначе говоря, MD = -^х^-100, А А/ где ЬК, Ai — изменения в цене и рыночной процентной ставке в%. Из приведенного выражения следует Д*=-0,0ШЯх КхМ.(11.25) Формула (11.25) применяется в практике для оценивания колебаний в цене облигаций при незначительных (до 1%) изменениях рыночной процентной ставки. ПРИМЕР 11.9. Для облигации примера 11.4 было найдено: D = 4,12 года, / = 19,62%. Откуда 4,12 Используем полученный параметр для оценки влияния на цену облигации ожидаемого повышения рыночного процента с 19,62 до 20%. Находим 247  ЛК = -0,01 х 3,44 х 65 х 0,38 = -0,85,т.е. при указанном повышении ставки курс облигации составит 65-0,85 = 64,15. §11.5. Оценивание займов и облигаций Методы оценивания. Оценивание займов представляет собой один из важнейших видов количественного финансового анализа, имеющего различные практические приложения. Поскольку займы часто реализуются посредством выпуска облигаций, то метод их оценивания обсудим применительно к облигациям, причем оценивание рассмотрим с позиции инвестора. Оценивание заключается в определении капитализированной суммы доходов от облигации (или другого вида займа), т.е. суммы денег, которая в финансовом отношении эквивалентна этим доходам с учетом сроков их выплат. Эта сумма равна современной стоимости доходов при некоторой заданной величине процентной ставки. В зависимости от постановки задачи — это существующая или ожидаемая ставка денежного рынка, или, наконец, ставка помещения. Нетрудно убедиться в том, что оценивание облигаций является задачей, обратной определению их полной доходности. Конкретные методы оценивания различных видов облигаций рассмотрим в той последовательности, которая была принята при определении их доходности. Облигации без обязательного погашения с периодической выплатой процентов. Напомним, что процесс выплаты процентов здесь можно рассматривать как вечную ренту. Современная стоимость такой ренты определена в гл. 5. Согласно этой формуле имеем: р-^и лг=4юо. Таким образом, курс такой облигации прямо пропорционален норме купонного дохода и обратно пропорционален рыночной ставке. Если доход выплачивается р раз в году, то О— £ JT = S. 1ЛЛ 248   ПРИМЕР 11.10. Пусть некоторый источник дохода постоянно приносит 8% годовых. Каков расчетный курс данных инвестиций при условии, что доход будет поступать достаточно продолжительное время, а ставка помещения берется на уровне 12%? Получим8 К=—100 = 66,67. Для того чтобы обеспечить доходность на заданном уровне, курс должен быть равен расчетной величине. Облигации без выплаты процентов (с нулевым купоном). Напомним, что здесь один источник дохода — разность между ценой приобретения и номиналом, если облигация погашается по номиналу. По определению Р= Nvn, K= Vя 100. Очевидно, что курс уменьшается вместе с ростом рыночной ставки и срока облигации. Облигации с выплатой процентов и номинала в конце срока. Общая сумма, которую получает владелец облигации при ее погашении, равна N(\ + g)n. Соответственно расчетная цена и курс при ставке помещения / составят (I + g\n (I + g\n Из последней формулы следует, что курс определяется тремя параметрами, причем влияние срока зависит от соотношения ставок g и /. Если g > /, то, как видим, с увеличением срока курс экспоненциально растет. ПРИМЕР 11.11. Пусть текущий доход от облигации выплачивается вместе с номиналом в конце срока; п = 5, д= 8% (начисление процентов поквартальное), / = 12%. В этом случае /(1 +0,08/4)4\5 «- Облигации с периодической выплатой процентов и погашением номинала в конце срока. Напомним, что доход от таких облига- 249 ций имеет два источника — периодически получаемые проценты и разность между ценой приобретения и выкупной ценой. Необходимые равенства для определения цены и курса таких облигаций были найдены выше (см. (11.6)—(11.10)).
Для определения расчетного курса по формулам (11.7) и (11.9) можно применить программу ПЗ пакета Excel (см. с. 110—111). Влияние факторов. Посмотрим, как влияют различные факторы на курс облигации. Для этого вернемся к равенству (11.7): Очевидно, что изменение купонной процентной ставки влияет только на второе слагаемое. Так, рост этой ставки увеличивает данное слагаемое и курс в целом, причем это увеличение линейно: чем больше рыночная ставка, тем это влияние меньше при всех прочих равных условиях. Что касается влияния рыночной ставки процента или ставки помещения, учитываемой в расчете, то повышение этой ставки приводит к сокращению обоих слагаемых курса облигации. Зависимость курса от размера рыночной ставки показана на рис. 11.3, на основе которого можно сделать один важный в практическом отношении вывод: чем больше срок облигации, тем чувствительней курс к изменению рыночной ставки (круче кривая). Сказанное объясняет тактику поведения инвесторов на рынке облигаций. Так, если ожидается повышение рыночной ставки, то инвесторы стремятся заменить долгосрочные облигации на облигации с меньшим сроком. При ожидании снижения ставки происходит обратное. 250 Степень влияния уровня рыночной ставки на курс облигации зависит и от размера купонной нормы дохода — чем она выше, тем меньше влияет изменение ставки. Указанная зависимость лежит в основе следующего правила поведения инвесторов: при ожидании повышения рыночной ставки для инвестора предпочтительней покупать облигации с высокой купонной доходностью и, наоборот, при понижении ставки для инвестора целесообразно вкладывать деньги в облигации с низкой купонной доходностью. 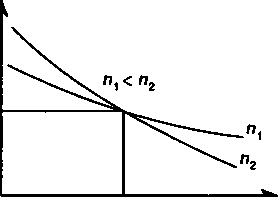 100 к Рис. 11.3 Перейдем к влиянию срока облигации. С увеличением срока величина первого слагаемого курса падает, второго растет при всех прочих равных условиях. Суммарный результат зависит от того, в каком соотношении находятся норма купонного дохода и рыночная ставка процента (см. рис. 11.4). На этом рисунке показано, что при g > i сокращение первого слагаемого перекрывается ростом второго. При равенстве нормы купонного дохода рыночной ставке изменения слагаемых курса полностью компенсируют друг друга. 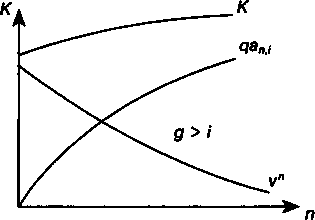 Рис. 11.4 251 Проблема оценивания облигаций существует не только тогда, когда облигация покупается или продается на рынке, но и когда она находится у владельца. В общем случае ее цена изменяется во времени даже в такой крайне редкой ситуации, когда рыночная процентная ставка остается постоянной и уж тем более, если эта ставка изменяется. С приближением даты погашения увеличивается современная стоимость суммы, получаемой при погашении облигации, одновременно уменьшается современная стоимость будущих поступлений по купонам. Какой бы ни была цена до погашения, в конце срока цена облигации равна номиналу или некоторой заранее фиксированной выкупной цене. ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
