Е. М. Четыркин финансовая математика

• Название: Е. М. Четыркин финансовая математика
• Анкор: chetyrkin_e_m_finansovaya_matematika.doc
• Дата: 22.04.2017
• Размер: 4.63 Mb.
• Имя файла: chetyrkin_e_m_finansovaya_matematika.doc
• Тип: Учебник; #4971
• страница: 13 из 58

§9.4. Льготные займы и кредиты

Грант-элемент. Предмет обсуждения в данном параграфе также связан с долгосрочными займами. Однако здесь они рас­сматриваются под другим углом зрения. Дело в том, что в ряде случаев долгосрочные займы и кредиты выдаются по тем или иным причинам (иногда политическим) под льготные для заем­щика условия. Низкая (относительно ставки на рынке креди­тов) процентная ставка в сочетании с большим его сроком и льготным периодом дают должнику существенную выгоду, ко­торую можно рассматривать как субсидию. Кредитор в этих ус­ловиях несет некоторые потери, так как он мог бы инвестиро­вать деньги на более выгодных условиях.

Проблема определения размера такого рода помощи обсуж­далась в международных организациях и экономической лите­ратуре главным образом с позиции межстрановых сопоставле­ний — для сравнения размеров финансовой помощи, оказыва­емой ряду развивающихся стран. Однако проблема оценки по­следствий выдачи льготных займов имеет более общее значе­ние, так как льготные займы предоставляют и внутри страны.

Грант-элемент (grant-element) — это условная потеря заимо­давца, которая связана с применением более низкой процент­ной ставки, чем существующие ставки кредитного рынка. Грант-элемент определяется в двух видах: в виде абсолютной и относительной величин.

Абсолютный фант-элемент рассчитывается как разность но­минальной суммы займа и современной величины платежей по погашению займов, рассчитанной по рыночной ставке. Проб­лема, как видим, сводится к выбору надлежащей ставки про­цента для расчета современной величины. Рекомендации по выбору конкретного значения этой ставки весьма расплывчаты. Обычно используют превалирующую на рынке долгосрочных кредитов ставку.

Размер абсолютного грант-элемента находим следующим об­разом:

W=D-G,(9.13)

где W'— абсолютный грант-элемент, D — сумма займа, G — со­временная величина платежей, поступающих в счет погашения займа, рассчитанная по реальной ставке кредитного рынка.

196

Относительный грант-элемент характеризует отношение аб­солютного грант-элемента к сумме займа:

W G

"-Т"¹-^' ^(9Л4)

w — относительный грант-элемент.

Как видим, все переменные приведенных формул определя­ются условиями выдачи и погашения займа.

Выведем рабочие формулы для расчета W и w при условии, что долг и проценты выплачиваются в виде постоянных сроч­ных уплат. Для анализа последствий выдачи льготных займов этого достаточно.

Пусть заем выдан на п лет и предусматривает выплату про­центов по льготной ставке g. На денежном рынке аналогичные по сроку и величине займы выдаются по ставке /. В этом слу­чае при отсутствии льготного периода срочная уплата составит:

Г=-Г", (9.15)

а современная величина всех выплат должника очевидно равна Кяг„._;. В итоге

n\i

а Л

(9.16)

W=D- Ya_ni=D\\-

°n\g I

w-1-7*4 (9.17)

где а .,, а_ио— коэффициенты приведения постоянных годовых рент постнумерандо, определенные для процентных ставок / и

ПРИМЕР 9.10. Льготный заем выдан на 10 лет под 3,8%. Предус­матривается погашение долга равными срочными уплатами. Из­вестно, что обычная рыночная ставка для такого срока займа рав­на 8%. В этом случае

^аю;8 . *-,<_ллв 0,038

* 10,3,8 ■ " 1,038
IV = 1 - -^- = 1 - 6,71008 х ₄ \ _мо__ю= 0,1809.

197

Допустим, исходная сумма займа равна 10 млн руб. Тогда аб­солютный грант-элемент или условная сумма потерь для кредито­ра и, соответственно, выгода для должника, составят

W = 10 х 0,1809 = 1,809 млн руб.

Наличие льготного периода увеличивает фант-элемент. Ес­ли в льготном периоде должник выплачивает проценты, то со­временная величина поступлений по долгу определяется как сумма двух элементов — современных величин процентных платежей в льготном периоде и срочных уплат в оставшееся время. Таким образом,

G= Dgxa_Li+Yxa_n__L;ixv^L,(9.18)

где п - L — продолжительность периода погашения задолжен­ности; L — продолжительность льготного периода.

После ряда преобразований (9.14) получим¹

G W-1---1-

Ь^-^ ⁺ *^xfld" (9.19)

V ^Un-L;g)

Здесь а_п-щ , ^„-t^ — коэффициенты приведения постоянных рент со сроком п — L и ставками / и g; v^L— дисконтный мно­житель по ставке /.

Обсудим еще один возможный вариант. Пусть в льготном периоде проценты начисляются, но не выплачиваются. Они присоединяются к основному долгу, который погашается в те­чение п — L лет. Условия такого займа более льготны для долж­ника, чем при последовательной выплате процентов.

Срочные уплаты и их современная величина в данном слу­чае равны:

D^+Jt _r-Yп На основе этих выражений получим

w = 1 - — = 1 - — х _t .

D^an-L* I 1 + I

См. Математическое приложение к главе.

198

ПРИМЕР 9.11. Пусть заем в примере 9.10 предусматривает трехлетний льготный период, в течение которого выплачиваются проценты. Для расчета относительного грант-элемента находим: а₇₈ = 5,20637, а₇₃₈ = 6,04667, а₃₈ = 2,5771, v³= 1.08"³ = = 0,79383;

w= 1 -

(5,20637

^6,04667

0,79383 + 0,038 х 2,5771 = 0,2185

Если проценты в льготном периоде не выплачиваются, а при­соединяются к основной сумме долга, то

_а5,20637 |Ч038^з
w = 1 - | _л_ | = 0,2356.

6,04667 1 1,08

Грант-элемент, как было продемонстрировано выше, — ус­ловная обобщающая характеристика льготности займа (потерь заимодавца и выигрыша должника). Сумма, которая равна грант-элементу, существенно зависит от принятой при ее оп­ределении процентной ставки. График зависимости относи­тельных потерь от соотношения процентных ставок показан на рис. 9.1 для сроков займа 5 и 10 лет без льготного периода, £=5%.

л = 10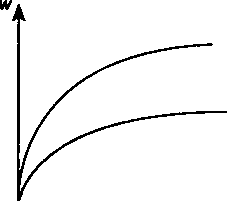

2 3

Рис. 9.1

л = 5

i/9

Предельным случаем льготного займа является беспроцент­ный заем. Выдача такого займа связана с потерями, которые оп­ределим, полагая, что соответствующие средства можно было бы разместить под проценты по рыночной ставке /. Например, уже при пятнадцатилетнем сроке беспроцентного займа и рыночной ставке 10% кредитор теряет почти 50% от суммы долга.

199

§9.5. Реструктурирование займа

Под реструктурированием займа (restructuring loan) понимают пересмотр условий действующего обязательства по погашению задолженности в связи с резким ухудшением финансового по­ложения должника — для кредитора, очевидно, лучше потерять кое-что, чем все.

При реструктурировании применяются разные приемы, ос­новными из которых являются:

• 
  прямое сокращение суммы долга,
  
• 
  уменьшение размера процентной ставки,
  
• 
  пересмотр сроков и порядка выплат процентов и сумм по­гашения основного долга.
  

На практике одновременно применяют несколько из указан­ных способов. Например, известны случаи, когда к одной час­ти обязательства применяли сокращение суммы основного дол­га, к другой — снижение процентной ставки, снижение про­центной ставки иногда сопровождается увеличением льготного периода и т.п.

В России регламентированы способы реструктурирования задолженности в бюджетную систему и в государственные вне­бюджетные фонды. В частности, предусматриваются нормати­вы для срока погашения в зависимости от отношения размера долга к общей стоимости имущества должника. Так, если долг не превышает 10% стоимости, то предусматривается минималь­ный срок, если долг составляет 45-50%, то производится рас­срочка погашения до 10 лет.

Какой бы способ реструктурирования ни был принят, обыч­ным ее следствием является уменьшение современной стоимо­сти выплат и снижение процентной ставки за задолженность. В силу того, что при реструктурировании изменяются многие ус­ловия погашения задолженности, точные финансовые послед­ствия этих изменений неочевидны. Поэтому выбор варианта реструктурирования и оценка финансовых последствий заклю­чаются в сравнении соответствующих расчетных параметров. Для получения последних необходимо сформировать варианты потоков платежей от должника. Далее на основе принятой для дисконтирования процентной ставки (превалирующая для дан­ного срока кредита рыночная ставка) рассчитать современную стоимость поступлений.

200

Что касается фактической доходности для кредитора новых условий займа, то здесь ограничимся лишь очевидным замеча­нием, что она будет ниже, чем до реструктурирования. Методи­ка расчета размера процентной ставки на основе показателей потока платежей обсуждалась в гл. 5.

ПРИМЕР 9.12. Реструктурируется долг в сумме 1000 ден. ед., срок 5 лет, без льготного периода, погашение задолженности по методу постоянных срочных уплат, выплаты постнумерандо, про­центы за кредит по ставке 12% годовых. Обсуждается два вари­анта:

• 
  увеличение срока до 8 лет, снижение платы за кредит до 11,5%;
  
• 
  увеличение срока до 10 лет, введение льготного периода 3 года, снижение платы за кредит до 11,75%.
  

При сравнении вариантов реструктуризации следует учесть, что на денежном рынке кредиты на аналогичные сроки и с близ­кой степенью надежности открывают по 12%. Предпочтительным для должника, естественно, является вариант с наименьшей сов­ременной стоимостью выплат. Для первого варианта находим:

D 1000

^/1" W ^А<" ^{У< к а8:,1:5 =} ^i7^{x 4}'^{96764 = 982Д}

Для второго варианта получим (см. (9.15)):

D

/о =

^а10-3;11,75

А₂= Dg₂х а_3;12 + У₂х a₁₀__3:i₂ ^х ^^{3 = 100}° ^х 0,1175 х 2,401831 + 1000

4,600164

х 4,563756 х 1,12"³ = 988,4;

А_А < А₂ < 1000.

§9.6. Ипотечные ссуды

Ссуды под залог недвижимости или ипотеки (mortgage) полу­чили широкое распространение в странах с развитой рыночной экономикой как один из важных источников долгосрочного финансирования. В такой сделке владелец имущества (mort­gagor) получает ссуду у залогодержателя (mortgagee) и в качестве

201

обеспечения возврата долга передает последнему право на пре­имущественное удовлетворение своего требования из стоимости заложенного имущества в случае отказа от погашения или не­полного погашения задолженности. Сумма ссуды обычно не­сколько меньше оценочной стоимости закладываемого имуще­ства. Наиболее распространенными объектами залога являются жилые дома, фермы, земля, другие виды недвижимости. Хара­ктерной особенностью ипотечных ссуд является длительный срок погашения.

Ипотечные ссуды выдаются коммерческими и специальны­ми ипотечными банками (например, земельными), различными ссудно-сберегательными ассоциациями. Ипотечный кредит для приобретения жилья начали практиковать и в России. Первой в этом отношении стала Москва. В 1999 г. этот вид кредита ста­ли открывать четыре кредитные организации. По условиям Ин-вестсбербанка и Собинбанка заемщик оплачивает 30% стоимо­сти квартиры, а на остальную сумму получает кредит на 10 лет по ставке 10% в валюте.

Существует несколько видов ипотечных ссуд, различающих­ся в основном методами погашения задолженности. Большин­ство видов являются вариантами стандартной или типовой ипотечной ссуды. Суть ее сводится к следующему. Заемщик по­лучает от залогодержателя (кредитора) некоторую сумму под за­лог недвижимости (например, при покупке или строительстве дома). Далее он погашает долг вместе с процентами равными, обычно ежемесячными, взносами.

Модификации стандартной схемы ипотеки нацелены на повышении ее гибкости в учете потребностей как должника, так и кредитора. Так, некоторые из них имеет целью снизить расходы должника на начальных этапах погашения долга, пе­ренося основную их тяжесть на более поздние этапы. Такие ипотеки привлекают тех клиентов, которые ожидают рост своих доходов в будущем, например, начинающих предприни­мателей и фермеров. Привлекательна такая ипотека и для мо­лодых семей при строительстве или покупке жилья. В других схемах тем или иным путем в большей мере учитывается про­центный риск. Кратко охарактеризуем некоторые схемы ипо­тек.

Ссуды с ростом платежей {graduated mortgage, GPM). Данный вид ссуды предусматривает постоянный рост расходов по об­служиванию долга в первые годы. В оставшееся время погаше-

202

ние производится постоянными взносами. Вариантом такой ипотеки является ссуда, погашение которой происходит по со­гласованному графику: каждые 3—5 лет увеличивается сумма взносов.

Ссуда с льготным периодом. В условиях ипотеки предпола­гается наличие льготного периода, в течение которого выпла­чиваются только проценты по долгу. Такая схема в наиболь­шей мере сдвигает во времени финансовую нагрузку долж­ника.

В последние два десятилетия в практику вошли и более сложные схемы погашения долга по ипотеке, преследующие в конечном счете те же цели — быть более гибкими и удобными для клиентов.

Как уже отмечалось, ипотечные ссуды выдаются на дли­тельные сроки. Даже в стабильной экономике это связано с определенным риском, в частности, риском изменения про­центной ставки на рынке кредитов. Некоторую страховку от такого риска обеспечивают условия ссуд, относящиеся к уровню процентной ставки. К таким ипотекам относятся сле­дующие.

Ссуды с периодическим изменением процентной ставки (rollover mortgage, RM). Схема этой ссуды предполагает, что стороны ка­ждые 3—5 лет пересматривают уровень процентной ставки. Та­ким образом, происходит периодически возобновляемое сред­несрочное кредитование при долгосрочном погашении всей за­долженности. Этим самым создается возможность для некото­рой, конечно неполной, адаптации к изменяющимся условиям рынка.

Ипотека с переменной процентной ставкой (variable-rate mort­gage, VRM). Уровень ставки здесь "привязывается" к какому-либо распространенному финансовому показателю или индек­су. Пересмотр ставки обычно осуществляется по полугодиям. Чтобы изменения ставок не были очень резкими, предусматри­ваются верхняя и нижняя границы разовых коррективов (на­пример, не более 2%).

Основной задачей при анализе ипотек является разработка планов погашения долга. Важно также уметь определить сумму остатка задолженности на любой момент процесса погашения. Ниже обсуждаются методы решения этих проблем для трех ипотечных схем.

203

§9.7. Расчеты по ипотечным ссудам

Наиболее распространенной является ипотечная ссуда, усло­вия которой предполагают равные взносы должника, взносы ежемесячные постнумерандо или пренумерандо. В договоре обычно устанавливается ежемесячная ставка процента, реже го­довая номинальная.

В осуществлении ипотеки при покупке (строительстве) объ­екта залога участвует три агента: продавец, покупатель (долж­ник), заимодавец (кредитор). Взаимосвязи между ними показа­ны на блок-схеме (см. рис. 9.2).

		ПРОДАВЕЦ
	ИМУЩЕСТ1 120	30 | ОПЛАТА J 100 + 20 V I
КРЕДИТОР	ССУДА 100	ПОКУПАТЕЛЬ
	ЗАЛОГ 100
	^
t_	ПОГАШЕНИЕ ДОЛГА	Я

Рис. 9.2

Продавец получает от покупателя за некоторое имущество полную его стоимость (120). Для этого покупатель получает ссу­ду под залог этого имущества (100) и добавляет собственные средства (20). Задача заключается в определении размера еже­месячных погасительных платежей R и остатка задолженности на момент очередного ее погашения вплоть до полной оплаты долга.

Поскольку погасительные платежи (взносы) представляют собой постоянную ренту, при решении поставленной задачи применим тот же принцип, что и при разработке плана погаше­ния долгосрочного долга равными срочными уплатами. Для этого приравняем современную величину срочных уплат сумме ссуды. Для месячных взносов постнумерандо находим:

/)= Ra

УУ;/>

где D — сумма ссуды; УУ— общее число платежей, N= Yin (n — срок погашения в годах); / — месячная ставка процента; R — ме-

204

сячная сумма взносов; a_N.. — коэффициент приведения посто­янной ренты.

Искомая величина взноса составит

Л =

^aw

= Dc.

(9.20)

В рамках решаемой проблемы величину с = \/a_N;iможно на­звать коэффициентом рассрочки. Для рент пренумерандо получим

R = —-(1+/).

(9.21)

Найденная по формуле (9.20) или (9.21) величина срочной уплаты является базой для разработки плана погашения долга. Согласно общепринятому правилу из этой суммы прежде всего выплачиваются проценты, а остаток идет на погашение долга.

ПРИМЕР 9.13. Под залог недвижимости выдана на 10 лет ссуда в размере 100 млн руб. Погашение ежемесячное постнумерандо, на долг начисляются проценты по номинальной годовой ставке 12%. Таким образом, N = 120, / = 0,01; находим: а_120;1 = 69,70052. Для этих условий ежемесячные расходы должника равны

Я =

100 000 69,70052

= 1434,709 тыс. руб.

Проценты за первый месяц равны 100 000 х 0,01 = = 1000 тыс. руб., на погашение долга остается. 1434,71 — 1000 = = 434,71 тыс. руб. План погашения долга представлен в таблице.

Месяц	Остаток долга на начало месяца	Взнос	Проценты	Погашение долга
1 2 3	100000,00 99565,29 99126,23	1434,71 1434,71 1434,71	1000,00 995,65 991,26	434,71 439,06 443,45
37 38 39	81274,07 80652,10 80017,63	1434,71 1434,71 1434,71	812,74 806,52 800,24	621,97 628,19 634,47
118 119 120	4219,35 2826,94 1420,50	1434,71 1434,71 1434,71	42,20 28,27 14,21	1392,5 1406,44 1420,50

205

Как показано в таблице, в первом месяце расходы на выплату процентов и погашение основного долга соотносятся как 1000:434,71; в последнем месяце — уже как 14,21:1420,5.

Перейдем к другой проблеме. При выдаче ссуды под залог для обеих сторон важно знать сумму погашенного долга и его остаток на любой промежуточный момент (необходимость в этом возникает, например, при прекращении договора или его пересмотре). С этой проблемой мы уже встречались выше при обсуждении метода погашения долга равными срочными упла­тами. Применительно к условиям стандартной ипотеки нахо­дим следующие соотношения:

d_t= м,

где d_t— сумма погашения долга, / — порядковый номер меся­ца, / — месячная ставка процента.

Остаток долга на начало месяца

Z),_+l = D_t- d_nt = l, ..., 12л.

Последовательные суммы погашения долга представляют со­бой геометрическую прогрессию с первым членом d_xи знаме­нателем (1+0, причем

d_{ = R- Di.(9.22)

Сумму членов этой прогрессии от начала погашения до / включительно найдем следующим образом:

^= <⁹-²³>

где s_ti— коэффициент наращения постоянной ренты постну-мерандо.

Остаток долга на начало месяца находим как разность

4+1 = ^1- ^Wr (9.24)

ПРИМЕР 9.14. По условиям ипотечного займа примера 9.13 най­дем остаток долга на начало, скажем, 118-го месяца:

206

D₁₁₈ = D, - W_U7\ IV₁₁₇ = cf_ts₁₁₇ = 434,71 x 220,3329 = 95780,65, откуда

D₁₁₈ = 100 000 - 95780,65 = 4219,35 тыс. руб.

Стандартная ипотека с неполным погашением задолженности и выплатой в конце срока остатка долга (balloon mortgage). Условия такой ипотеки позволяют уменьшить размеры периодических взносов и (или) сократить срок ссуды. Срочные уплаты рассчи­тываются таким образом, что они не покрывают всей задолжен­ности, остаток (balloon), обозначим его как /?, выплачивается в конце срока. Уравнение, балансирующее условия ипотеки, име­ет вид

D= Ra_Ni+ Bv^N.

Баланс достигается одним из следующих способов:

а) задается размер срочных уплат, определяется величина В:

Я=(1 +i)^N(D-Ra_Ni)-

б) задается /?, определяется размер срочных уплат:

Z). - Bv^N
R = — .

^aNj

Далее расчет ведется по уже рассмотренной схеме.

Ссуда с периодическим увеличением взносов. В этом варианте ипотеки задается последовательность размеров взносов. Пусть увеличение взносов происходит через равные интервалы време­ни т. В пределах каждого интервала взносы постоянны. Оче­видно, что для полной сбалансированности схемы размер пос­леднего взноса не задается, он определяется по сумме остатка задолженности.

Пусть /?,,..., R_k— размеры взносов. Определим размер пос­леднего взноса. Для этого найдем на начало операции сумму современных стоимостей взносов от первого до к - 1. Обозна­чим ее как Q:

1

207

Современная стоимость непокрытой взносами задолженно­сти на начало последнего периода

W= D- Q,

откуда размер взносов в последнем периоде ипотеки

W

Математическое приложение к главе

Доказательство формулы (9.19) Исходное равенство

„-,-!.

Современная стоимость поступлений по рыночной ставке / равна

G=Dgxa_L;i+ Ya_n__L;y.

По определению

Г =

⁴n-L%

откуда

_i=^s_°«⁺_T-°-«*^L_-

'n-L*

Таким образом,

\^a"-L;g

w-1-

ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА

Четыркин Е.М. Методы финансовых и коммерческих расчетов. М: Дело, 1995. Гл. 7,8.

Глава 10 ИЗМЕРЕНИЕ ДОХОДНОСТИ