Е. М. Четыркин финансовая математика

• Название: Е. М. Четыркин финансовая математика
• Анкор: chetyrkin_e_m_finansovaya_matematika.doc
• Дата: 22.04.2017
• Размер: 4.63 Mb.
• Имя файла: chetyrkin_e_m_finansovaya_matematika.doc
• Тип: Учебник; #4971
• страница: 10 из 58

Глава 7

ОПРЕДЕЛЕНИЕ

БАРЬЕРНЫХ ЗНАЧЕНИЙ

ЭКОНОМИЧЕСКИХ ПОКАЗАТЕЛЕЙ

§7.1. Общая постановка задачи. Линейная модель

В практике финансово-экономического анализа довольно часто возникает необходимость определить барьерное (порого­вое, критическое, предельно допустимое) значение некоторо­го параметра. Под барьерным значением параметра понимает­ся такая его величина, превышение которой приводит к поло­жительному или, наоборот, отрицательному конечному эконо­мическому результату в рамках некоторой производственной или финансовой системы. Например, если речь идет об опре­делении объема производства какого-то продукта, то порого­вым его значением является такой объем выпуска, при кото­ром полученная прибыль равна нулю. Превышение этого объ­ема дает прибыль, производство в меньшем объеме оказывает­ся убыточным. Подобная и многие другие, сходные по общей постановке, задачи решаются с помощью метода барьерной или критической точки (break-even point). Метод барьерной точки широко используется в финансовом проектировании, при раз­работке бизнес-планов и при решении разнообразных проб­лем: при определении порогового значения процентной став­ки, цены товара, срока выполнения финансовой операции и т.д.

Наиболее простая постановка задачи осуществляется с помо­щью линейной модели, которая и рассматривается в данном па­раграфе. Разумеется, такая постановка не является единственно возможной. Некоторые пути для дальнейшего развития метода предлагаются в следующих парафафах главы. Причем часть из рассмотренных здесь проблем, например барьерные точки для налоговых ставок и барьерные точки в условиях неопределен­ности, до сих пор не обсуждались в финансовой литературе.

149

Заметим, что до недавнего времени метод барьерной точки применялся, так сказать, в статике. Экономические показатели рассматривались в рамках одного, сравнительно короткого пе­риода. В последнее время этот метод распространяется и на по­токи платежей, охватывающих ряд последовательных времен­ных интервалов. В этих случаях с помощью дисконтирования стал учитываться важнейший фактор — время (а именно, сро­ки инвестирования и сроки отдачи от инвестиций).

Для начала рассмотрим наиболее простой и весьма условный вариант статической постановки задачи, к которому обычно прибегают при объяснении сути метода. Пусть необходимо най­ти пороговый объем производства одного вида продукта при ус­ловии, что все необходимые для анализа количественные зави­симости описываются линейными выражениями, иначе говоря, применяется линейная модель.

Для записи такой модели примем обозначения:

Q — объем производства (в натуральном или условно-нату­ральном измерении);

F — постоянные производственные затраты, затраты, не за­висящие от объема выпуска;

с — переменные, или пропорциональные затраты (в расчете на единицу продукции);

р — цена единицы продукции;

S — общая сумма затрат;

V — стоимость выпущенной продукции;

Р — размер прибыли до уплаты налогов.

Переменные Q, F, S, V, Р определяются в расчете на одина­ковый интервал времени, обычно на один год.

Для начала найдем стоимость выпущенной продукции и со­ответствующую сумму затрат:

V=_PQ,(7.1)

S=F+cQ.(7.2)

Искомый критический объем производства или барьерную точку получим на основе равенства стоимости выпущенной продукции и суммы затрат: V- S. Именно равенство двух раз­нородных экономических показателей, каждый из которых яв­ляется функцией одной управляющей переменной (в рассматри-

150

ваемом случае — объема производства), лежит в основе метода барьерной точки.

Обозначим барьерный объем производства как Q_k, тогда, ис­пользуя (7.1) и (7.2), получим

_PQ_k = cQ_k+ F.

Таким образом,

Как видим, чем выше размер постоянных и переменных за­трат, тем больше критический объем производства.

Прибыль (до выплаты налогов) по определению составит

Р= V- S=(p-c)Q- F.(7.4)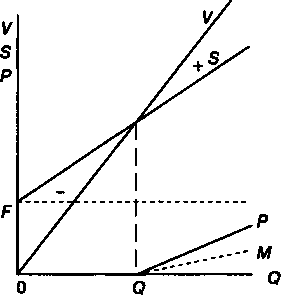





Рис, 7Л

151

Графическая иллюстрация постановки задачи и ее решения приведена на рис. 7.1. Решение находится в точке пересечения двух линий, одна из которых характеризует динамику затрат (5), другая — изменение дохода (У) по мере увеличения выпуска. Объемы производства, которые меньше критического Q_k, при­ведут к убыткам. Превышение этого объема дает прибыль. Чем выше размер постоянных и переменных затрат, тем больше критический объем производства. Чистая прибыль после упла­ты налогов (пропорциональных прибыли) характеризуется на рис. 7.1 линией Л/.

ПРИМЕР 7.1. Ожидается, что р = 50, с = 30, F = 100. Находим

100 °^к= 50 - 30 ^{= 5}' ^{Р= (5}° " ³⁰⁾° " ¹°°-

Графическое изображение условий задачи и ее решение пред­ставлено на рис. 7.2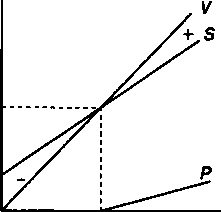

250

V S

100

0 5 I

Рис. 7.2

Рассмотренный метод базируется на реальных данных бух­галтерского учета или ожидаемых их величинах. Капиталовло­жения учитываются посредством включения в затраты аморти­зационных отчислений.

Заметим, что все участвующие в расчете параметры рассма­триваются как константы. Между тем, с течением времени они безусловно изменяются и найденная для одного момента вре­мени критическая точка не окажется таковой для другого мо­мента. Важно также подчеркнуть, что время, как важнейший финансовый фактор, не принимается здесь во внимание. Такой подход вполне оправдан, если капиталовложения уже осущест­влены и встает вопрос только о выборе видов производимой продукции и их объемов.

Сказаное выше позволяет сформулировать общее определе­ние для обсуждаемого метода, как способа расчета барьерного значения управляющей переменной исходя из равенства двух "кон­курирующих" функций этой переменной. Содержание управляю­щего параметра и функций, как видим, определяется конкрет­ными условиями решаемой задачи. В рассмотренном выше примере управляющей переменной является объем производст­ва, "конкурирующими" функциями — доход (выручка) и затра­ты.

152

§7.2. Нелинейные модели

Линейная модель во многих случаях дает практически прие­млемое описание ситуации. Однако могут иметь место ситуа­ции, когда процесс формирования затрат и/или стоимости про­дукции более адекватно описывается нелинейными функциями и имеются достаточно надежные данные для получения соот­ветствующих кривых. Вид и параметры таких кривых могут быть установлены, например, в ходе статистического анализа или их можно задать экспертно.

Барьерный выпуск продукции. Вернемся к задаче по опреде­лению критического объема продукции, но в условиях, когда одна или обе "конкурирующих" функции являются нелиней­ными. Ограничимся двумя из возможных постановок задачи. Пусть для начала стоимость продукции — линейная функция выпуска, а затраты на производство описываются нелинейной, монотонно растущей функцией. Иначе говоря, предполагает­ся, что удельные затраты сокращаются по мере роста масшта­бов производства, а цена единицы продукции не изменяется. Такое сочетание затрат и стоимости продукции представлено на рис. 7.3.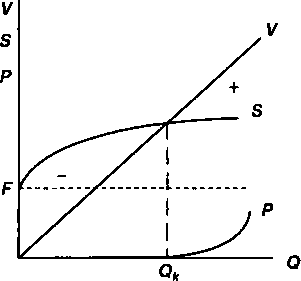



Рис, 7,3

Задача, как и выше, заключается в определении барьерного уровня выпуска продукции. Стоимость продукции находится по формуле (7.1), а сумма переменных затрат описывается, допус­тим, степенной функцией cQ^h, причем 0 < А < 1. В этом случае общая сумма затрат составит

153

5= F+ cQ^h

Разность "конкурирующих" функций в барьерной точке рав­на нулю:

pQ_kcQ\- F=0.

Решение, как видим, сводится к нахождению корня этого уравнения.

ПРИМЕР 7.2. Исходные данные: F Соответственно имеем		= 100, p =		50, с = 40, h	= 0,5.
	50Qk- 40Q°'5 -	- 100	= 0.
Найдем корни этого уравнения. квадратное, положив О = z2. После		Для чего	этого преобразуем получим		его в
*«-■	50z2 - 40z -	100 =	= 0,
	-(-40)±^40)2 27	-4х! 50	50 х(-	-юо)
Положительный = 1,862 = 3,46.	корень равен	1,86.	Таким образом,		°*=

Перейдем к сочетанию двух нелинейных зависимостей. На­пример, пусть обе функции являются параболами второй степе­ни (см. рис. 7.4). Тогда

V= aQ²+ bQ, S=cQ² + dQ +F,

где a, b, c, d — параметры парабол.

Прибыль в зависимости от уровня выпуска составит

Р = {а - c)Q² + {b-d)Q- F(7.5)

Барьерный объем выпуска находится как корень квадратно­го уравнения

(a-c)Q²_k + (b-d)Q_k-F=0. 154



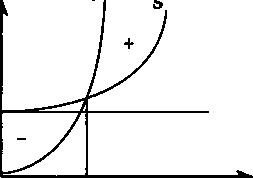
v, s

F

O_k 0

Рис. 7.4

Добавим, что при некоторых условиях можно рассчитать объем выпуска, максимизирующего размер прибыли (обозначим его как Q_m). Для этого, как известно, достаточно найти произ­водную функции прибыли и приравнять ее нулю. В случае, ко­гда прибыль описывается выражением (7.S), находим

^g»-t^t- <⁷-⁶>

Как видим, положение точки максимума полностью опреде­ляется параметрами соответствующих парабол. Причем необхо­димым условием существования максимума являются следую­щие соотношения: d>b, a>c . Если же b>d и а>с, то прибыль монотонно растет вместе с увеличением выпуска.

Нелинейную модель можно представить и в неформализо­ванном виде — как таблицу данных, характеризующих затраты и стоимость продукции в зависимости от размера выпуска (см. пример 7.3).

ПРИМЕР 7.3. В приведенной ниже таблице и на диаграмме со­держатся данные о затратах, стоимости продукции и ожидаемой прибыли.

о	F	с	Р	S	V	Р
0	100	—	—	100	—	—
5	100	30	50	250	250	0
10	100	27	50	370	500	130
15	100	22	45	430	675	145
20	100	20	40	500	800	300
25	100	20	30	600	750	150

155

V, S, P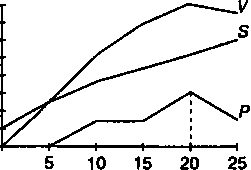

800

700-

600-

500-

400

300-

200

100-

0

Рис, 7,5

Наибольшая прибыль, как видим, приходится на выпуск, рав­ный 20.

§7.3. Барьерные показатели в финансовом анализе

Сравнение денежных сумм. Начнем с решения простой зада­чи, иллюстрирующей возможности метода при решении неко­торых проблем финансов и кредита. Допустим, необходимо вы­брать один из двух вариантов поступлений денежных средств, различающихся суммами и сроками: 5,, S₂со сроками л,, л₂, причем S₂> 5,, п₂ > п_х(иначе задача не имеет экономического смысла). Логически оправданно выбор обосновать на сравне­нии современных стоимостей поступлений. Таким образом, ре­зультат выбора зависит от ожидаемого рыночного уровня про­центной ставки. Барьерной в рассматриваемой задачей являет­ся ставка, при которой оба варианта оказываются эквивалент­ными.

Рассмотрим метод решения для двух вариантов расчета сов­ременных стоимостей: по простой и сложной процентным став­кам. Для простой ставки имеем следующее равенство современ­ных стоимостей:

i + V* i + «A' ⁽⁷'⁷⁾

а для сложной ставки:

*i(l + '*P -S₂(l + '*P- (7.8)

156

В обоих равенствах i_kозначает величину барьерной ставки. Решив уравнение (7.7) относительно искомой ставки, получим

. s₂-s_x

^к5.л, - Д,я,

'1"2

^J2"\

(7.9)

Из последнего выражения следует необходимое условие для существования барьерной ставки

S_{n₂ > S₂n_xили S_{> Sj—.

^П2

Графическая иллюстрация решения представлена на рис. 7.6. ^рA ^p2_t



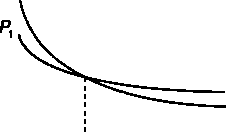
Рис- 7,6

Как видно из рисунка, если ожидаемый уровень ставки меньше барьерного, то для получателя денег предпочтителен вариант S₂, если же рыночная ставка больше барьерной, то сле­дует остановиться на альтернативном варианте.

ПРИМЕР 7.4. Сравним два варианта платежей с параметрами: S₁ = 1; S₂ = 1,15; n_t = 7; п₂= 12 (сроки платежей указаны в ме­сяцах). Сначала проверим: если

S_t > 1,15 х —i следовательно, решение существует. Далее по­лучим

115-1
/; = т£ у- = 0,4557, или 45,6%.

1Х--1.15*-

Таким образом, при рыночной ставке, которая меньше чем 45,6%, для получателя денег предпочтительней более отдаленная выплата при всех прочих равных условиях.

157

Перейдем к определению барьерного значения сложной ставки. На основе (7.8) находим

Откуда

HS₂ I 5,)

hi + <*) = -^-^--

В итоге

/* = ал/!п(1 + i_k)- 1. (7.10)

ПРИМЕР 7.5. Возможны два варианта оплаты товара при его по­ставке. Стоимость и сроки поставки: S₁ = 1; S₂ = 1,4; п₁ = 1; п₂= 2,5 (сроки измерены в годах). Покупателю необходимо вы­брать вариант покупки при условии, что срок не имеет решающе­го значения, иными словами, он должен ориентироваться только на величину выплат.

Находим величину барьерной ставки, при которой дисконтиро­ванные размеры затрат окажутся одинаковыми:

1п(1 +/_я) = "7у-= 1.22431;

i_k = ant In 0,22431 - 1 =0,251.

Итак, если рыночная ставка будет меньше 25,1%, то для поку­пателя окажется предпочтительней второй вариант.

Выбор варианта депозита. Метод определения барьерной точ­ки с использованием кривой доходности при выборе варианта депозита с наибольшей доходностью рассмотрен в гл. 4, пример 4.21. Поэтому на этой проблеме больше останавливаться не бу­дем. Дополнительные примеры применения метода барьерной точки в финансовом анализе будут рассмотрены в других главах.