Е. М. Четыркин финансовая математика

• Название: Е. М. Четыркин финансовая математика
• Анкор: chetyrkin_e_m_finansovaya_matematika.doc
• Дата: 22.04.2017
• Размер: 4.63 Mb.
• Имя файла: chetyrkin_e_m_finansovaya_matematika.doc
• Тип: Учебник; #4971
• страница: 8 из 58

§5.3. Современная стоимость постоянной ренты постнумерандо

Годовая рента. Напомним, что под современной стоимостью потока платежей понимают сумму дисконтированных членов этого потока на некоторый предшествующий момент времени. Вместо термина "современная стоимость" (современная вели­чина) потока платежей в зависимости от контекста употребля­ют термины капитализированная стоимость или приведенная ее-личина. Как было показано выше, современная стоимость пото­ка платежей эквивалентна в финансовом смысле всем плате­жам, которые охватывает поток. В связи с этим данный показа­тель находит широкое применение в разнообразных финансо­вых расчетах (планирование погашения долгосрочных займов, реструктурирование долга, оценка и сравнение эффективности производственных инвестиций и т.д.). В общем виде метод оп­ределения современной величины потока платежей (метод пря­мого счета) рассмотрен в § 5.1. Здесь же объектом анализа яв­ляется постоянная финансовая рента постнумерандо.

Методы расчета современных стоимостей финансовых рент обсудим в том же порядке, что и методы наращения рент и поч­ти столь же детально. Начнем с самого простого случая — го­довой ренты постнумерандо, член которой равен R, срок ренты — п, ежегодное дисконтирование. Рента немедленная. В этих условиях дисконтированная величина первого платежа равна Rv, второго — Rv², последнего — Rv". Как видим, эти величи­ны образуют ряд, соответствующий геометрической профессии с первым членом Rv и знаменателем v. Обозначим сумму чле­нов этой профессии через А:

A-Ryv' = Rv- --R—^V--

h v-i

/ х- (5-14)

1- (l + i)

I

Назовем множитель, на который умножается R, коэффициен­том приведения ренты, он обозначен как а_пЧ(в литературе встречается обозначение a_n,j). Этот коэффициент характеризует современную стоимость ренты с членом, равным 1. Значения a_n;iтабулированы (см. табл. 7 Приложения).

107

Поскольку рассматриваемый параметр часто применяется в финансовых расчетах, полезно, обратить внимание на некоторые его свойства. Очевидно, что чем выше значение /', тем меньше величина коэффициента. Нетрудно показать, что при / = О

%=о ^{= Л}-

При увеличении срока ренты величина а_пЛстремится к не­которому пределу. При п = » предельное значение коэффици­ента составит

lim

!-(!♦«)-

(5.15)

Полученное выражение применяется при расчете современ­ной стоимости вечной ренты, о чем пойдет речь в § 5.5.

График зависимости а_пЧот п показан на рис. 5.2.

Воспользуемся формулой (5.14) для определения взаимосвя­зи коэффициентов приведения ограниченной и вечной рент:

"„;/ =

1

(1 + /Г" 1 1

_{. =7 " °} ⁺ _°"^х _у ⁼ _{° "} ^уМ)а_*^т

В последней записи искомый коэффициент приведения оп­ределен как доля коэффициента приведения вечной ренты, за­висящая от срока ренты.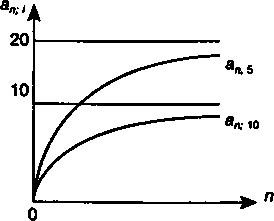



Рис. 5.2

ПРИМЕР 5.9. Годовая рента постнумерандо характеризуется па­раметрами: Я = 4 млн руб, п = 5. При дисконтировании по слож­ной ставке процента, равной 18,5 % годовых, получим

108

1 - 1.185"^5
А= 4a*iRs = ^{4 х} ГТ^ = ^{4 х} 3,092 = 12,368 млн руб.

5,18,5 о,185

Таким образом, все будущие платежи оцениваются в настоя­щий момент в сумме 12,368 млн руб. Иначе говоря, 12,368 млн руб., размещенных под 18,5% годовых, обеспечивают ежегодную выплату по 4 млн руб. в течение 5 лет.

Заметим, что формула (5.14) может быть применена и для определения современной стоимости /ьсрочной ренты. В этом случае переменная п означает число периодов ренты, а / — став­ку за один период (но не годовую).

Коэффициент приведения ренты за срок п = л, + п₂опреде­ляется следующим образом:

^ан;1 - Я*,;/

+ в|.₂У¹- (5.16)

Годовая рента, начисление процентов т раз в году. Не будем выводить формулу для этого случая, а просто заменим в форму­ле (5.14) дисконтный множитель (1 + /)^/| на эквивалентную ве­личину (1 + j/m)^mn, соответственно, / заменим на (1 + j/m)^m-— 1, после чего имеем:

1 -(1 +7/тГ'™

Л = R _/л, .. _чт — = Ra_mn._i/m.(5.17)

(1 +у//и)^т - 1 ^mnj/m

Рента /^-срочная (т = 1). Если платежи производятся не один, а р раз в году, то коэффициенты приведения находятся так же, как это было сделано для годовой ренты. Только теперь размер платежа равен R/p, а число членов составит пр. Сумма дисконтированных платежей в этом случае равна

А - - ? v^t/p- R _r¹"'^1+l' - Ra^{p). (5.18)

ПРИМЕР 5.10. В первой главе упоминалась авария на химиче­ском заводе в Бхопале (Индия). Корпорация "Юнион Карбайд" предложила в качестве компенсации пострадавшим 200 млн долл., выплачиваемых в течение 35 лет. Предложение было от­клонено ("За рубежом". 1985. № 11). Предложенная компенсация

109

эквивалентна 57,5 млн долл., выплаченных единовременно. Пока­жем, как была рассчитана эта сумма.

Если выплаты производятся помесячно на протяжении 35 лет равными суммами, то данный ряд платежей представляет собой постоянную ренту (р = 12) с годовой суммой выплат 200/35 = = 5,714 млн долл. в год. Допустим, это рента постнумерандо. То­гда согласно (5.18), положив / = 10% , получим

1 - 1,1-35 А= 5,714 _{1 11/12} _ = 57,59 млн долл.

Иначе говоря, капитал в сумме всего 57,59 млн долл. при на­числении 10% годовых достаточен для выполнения обязательства.

Рента ^-срочная (р = /и). Число членов ренты здесь равно числу начислений процентов; величина члена ренты составляет R/m . В итоге

R 1 -(1 +7/w)-"^w 1 -(1 +у/тГ™

А = х = R : . (5.19)

т j/m j

Этот же результат можно получить и по формуле (5.14) и при этом воспользоваться таблицей коэффициентов приведения по­стоянных рент. В этом случае вместо числа лет берется количе­ство периодов ренты, процентная ставка и величина члена рен­ты определяются соответствующим образом.

Для расчета современной стоимости платежей ренты с усло­вием р = т можно воспользоваться программой ПЗ (PV) паке­та Excel, которая определяет величину А с учетом единовремен­ного взноса в конце срока. Расчет производится по формуле

А = R х a_n;i+ БС х (1 + /Г^Л,

где R — член ренты, БС — единовременный взнос, a_n;i— коэф­фициент приведения постоянной ренты, п — число'периодов выплаты ренты и начисления процентов, / — процентная став­ка за период.

Последовательность действий при использовании программы ПЗ

1. 
   Последовательно вызвать: £, "финансовые функции", ПЗ.
   
2. 
   Показать в строках окошка условия выплаты ренты, размер единовременного платежа и порядок начисления процентов:
   

по

Норма — ставка начисляемых процентов за период, Клер — число периодов,

Выплата — член ренты; показывается с отрицательным знаком,

БС — единовременный взнос в конце срока, показывает­ся с отрицательным знаком. Если эта величина не указы­вается, то результат — современная стоимость постоянной ренты,

Тип — вид ренты, указать 0 для ренты постнумерандо и 1 — для ренты пренумерандо. Если вид ренты не указывает­ся, то расчет ведется для ренты постнумерандо.

После выполнения действий 1—2 в итоговой строке Значе­ние автоматически показывается расчетная величина. После на­жатия кнопки ОК эта величина показывается в выделенной ячейке таблицы Excel.

ПРИМЕР 5.11. Параметры ренты пренумерандо: R = 100 (годо­вая выплата), п= 5, р = т= 2. Общее число платежей — 10, ставка за полугодие 6%. Введем параметры в окошко програм­мы ПЗ:

Норма: 6%, Кпер: 10, Выплата: -50, Тип: 1, Ответ: 390,085.

Рента /ьсрочная (р * т). Сумма членов соответствующей прогрессии составит

Л ⁼ а _г/, , .. _Чт/я — - &^а .и• (5.20)

Ренты с непрерывным начислением процентов. Пусть, как и выше, ряд состоит из ежегодных платежей, равных Л, однако проценты начисляются непрерывно, сила роста равна 6. При дисконтировании по этой ставке всех членов ряда получим геометрическую прогрессию с первым членом R и знаменате­лем ё^ь. Сумма членов прогрессии находится следующим об­разом:

1 - е"^6я
A-R-j—^-Ra^.(5.21)

ill

Если имеет место р-срочная рента с непрерывным начисле­нием процентов, то

1 — е^Ьп
А = R—TJTn—77 = Л!^ (5.22)

ПРИМЕР 5.12. Для условий примера 5.9 при 6 = 0,185 находим

1 _ _е-0,185х5
^{А= 4} о,185 - ^{= 11} »^{878 МЛН Р}У^б>

Сравнение современных стоимостей рент постнумерандо с раз­ными условиями. Как следует из приведенных примеров, вели­чина современной стоимости заметно зависит от условий нара­щения процентов (точнее, дисконтирования) и частоты выплат в пределах года. Ниже приводятся соотношения современных стоимостей соответствующих рент. Современные стоимости обозначены как А(р;т), причем запись А(\;1)означает годовую ренту с ежегодным начислением процентов, А(р; ») относится к /ьсрочной ренте с непрерывным начислением процентов.

Для одних и тех же годовых сумм выплат и процентных ста­вок (/ =у =6) получим следующие неравенства:

А( 1;») < А( 1 ;/и) < Л( 1; 1) < А(р;*>) < А{р\т) < А{р\т) < А(р\т) < А(р; 1).

т>р>\ р=т>1 р>т>\

Из приведенных неравенств, в частности, следует, что рента с условиями р = 4 и т = 2 имеет меньшую современную стои­мость, чем рента с/; = 2и/и = 4.

Зависимость между наращенной и современной стоимостью ренты. В § 5.2 была показана зависимость между А и S произ­вольного потока платежей (см (5.3)). Для годовых и р-срочных постоянных рент постнумерандо с ежегодным начислением процентов находим

1 - (1 + /Г" (1 + 0^я - 1
А(\ + /)^л = R ———0 + 0^я = Я¹ : = S. (5.23)

Аналогичным образом получим

Svⁿ= A.

112

Для рент с начислением процентов т раз в году имеем

А{\ +j/m)^mn = 5, (5.24)

S(l +j/my^mn = A.(5.25)

Нетрудно догадаться, что в аналогичной зависимости нахо­дятся и коэффициенты наращения и приведения. В частности,

a_n;i(\ + 0- = 5_Л;/, s_n;iv» = а_п._г

ПРИМЕР 5.13. Найдем современную стоимость для варианта ренты р = т= 4, взяв за основу S = 31,785 (см. пример 5.6). По формуле (5.24) получим

/ 0,185 V²⁰ А= 31,785 1 + —_А— = 12,868 млн руб.

§5.4. Определение параметров постоянных рент постнумерандо

Как было показано выше, постоянная рента описывается на­бором основных параметров — R, п, / и дополнительными па­раметрами р, /и. Однако при разработке контрактов и условий финансовых операций могут возникнуть случаи, когда задается одна из двух обобщающих характеристик — S или А, и необхо­димо рассчитать значение недостающего параметра.

Определение размера члена ренты. Исходные условия: задает­ся S или А и набор параметров, кроме Л. Например, за обусло­вленное число лет необходимо создать фонд в сумме S путем систематических постоянных взносов. Если рента годовая, по­стнумерандо, с ежегодным начислением процентов, то, обра­тившись к (5.6), получим

R = -^-. (5.26)

^Sn;i

Пусть теперь условиями договора задана современная стои­мость ренты. Если рента годовая (т = 1), то из (5.14) следует

R = —. (5.27)

113

Таким образом, если ставится задача накопить за определен­ный срок некоторую сумму 5, то прибегают к формуле (5.26), если же речь идет о погашении задолженности в сумме А, то следует воспользоваться (5.27).

Аналогичным образом можно определить R и для других ус­ловий ренты.

ПРИМЕР 5.14. Известно, что принц Чарльз при разводе с Диа­ной выплатил последней 17 млн ф.ст. Как сообщалось, эта сумма была определена в расчете на то, что принцесса проживет еще 50 лет (увы, это не сбылось). Указанную сумму можно рассматривать как современную стоимость постоянной ренты. Определим раз­мер члена этой ренты при условии, что процентная ставка равна 10%, а выплаты производятся помесячно.

По условиям задачи А= 17 млн ф.ст., п= 50, р = 12, / = 10%. Для ренты постнумерандо с указанными параметрами можно за­писать

1 - 1 1"⁵⁰ 17 000 = ЛЦ*_Ю= ^я₁₂(1,11Ла-₁₎¹'^1,/12-

Ежемесячная выплата составит Я/12 = 135,6 тыс. ф.ст.

Расчет срока ренты. При разработке условий контракта ино­гда возникает необходимость в определении срока ренты и, со­ответственно, числа членов ренты. Решая полученные выше выражения, определяющие S или А, относительно л, получим искомые величины. Так, для годовой ренты постнумерандо с ежегодным начислением процентов находим

_{-(И _±i$L}

^П1п(1 +0 ' ^л 1п(1 + 0 •

Аналогичным образом определим сроки и для других видов рент. Сводка формул, полученных для различных рент постну­мерандо с дискретным начислением процентов, приведена в табл. 5.1.

Все приведенные выше формулы для определения я, разуме­ется, пригодны и в случаях, когда заданными являются коэф­фициенты приведения или наращения рент, поскольку а_пЧ= = A/R, s_n;i= S/R и т.д.

При расчете срока ренты необходимо принять во внимание следующие моменты.

114

Формулы для расчета срока постоянных рен

Количество	Количество начислений		Исходны
платежей		S
	от = 1 от > 1	1пф+П	(5.28)
/> = i		" 1п(1 + /)
		ln{jl(l+j/mr-l) + l}	(5.30)
		от1п(1 + у/от)
	от= 1 т= р т * р	1п{^[(1 + О'/" - 1] + 1}	(5.32)
Р>\		1п(1 + /)
		1пф+1)	(5.34)
		/nln(l +у/от)
		ln{^p[(l+y/m)^-l] + l}	• (5.36)
		/nln(l + j/m)

1. 
   Расчетные значения срока будут, как правило, дробные. В этих случаях для годовой ренты в качестве п часто удобно при­нять ближайшее целое число лет. У /ьсрочной ренты результат округляется до ближайшего целого число периодов пр. Напри­мер, пусть для квартальной ренты получено п = 6,28 лет, отку­да пр = 25,12 кварталов. Округляем до 25, в этом случае п = 6,25 лет.
   
2. 
   Если округление расчетного срока производится до мень­шего целого числа, то наращенная сумма или современная сто­имость ренты с таким сроком оказывается меньше заданных размеров. Возникает необходимость в соответствующей ком­пенсации. Например, если речь идет о погашении задолженно­сти путем выплаты постоянной ренты, то компенсация может быть осуществлена соответствующим платежом в начале или конце срока, или с помощью повышения суммы члена ренты.
   

Обсудим еще одну проблему, связанную со сроком ренты. Пусть А — текущее значение долга. Если он погашается с по­мощью постоянной ренты, то из (5.14) следует, что долг может быть погашен за конечное число лет только при условии, что R > AL Аналогичные неравенства можно найти и для других ви­дов рент. Если условия ренты таковы, что имеет место равенст­во, например, R = Ai₉то п = оо₉т.е. рента окажется вечной и долг практически не может быть погашен.

ПРИМЕР 5.15. Какой необходим срок для накопления 100 млн руб. при условии, что ежемесячно вносится по 1 млн руб, а на накопле­ния начисляются проценты по ставке 25% годовых? Имеем Я = 12, / = 25%. По формуле (5.32) находим

In п= —

-^-12(1,25¹/i2- 1) + 1

1п1,25

= 4,7356 года.

Если срок округляется до 5 лет, то необходимо несколько уменьшить размер члена ренты, т.е. найти член ренты для п= 5. В этом случае ежемесячный взнос должен составить 914,79 тыс. руб. (см. (5.26)).

Определение размера процентной ставки. Необходимость в определении величины процентной ставки возникает всякий раз, когда речь идет о выяснении эффективности (доходности) соответствующей финансово-банковской или коммерческой операции. Заметим, что расчет процентной ставки по осталь-

116

ным параметрам ренты не так прост, как это может показать­ся на первый взгляд. В простейшем случае задача ставится сле­дующим образом: решить уравнения (5.4) или (5.14) относи­тельно /. Нетрудно убедиться в том, что алгебраического реше­ния нет. Для получения искомой величины раньше прибегали к линейной интерполяции или какому-либо итерационному методу. В современных условиях для определения ставки по за­данным параметрам постоянной ренты удобно воспользовать­ся пакетом Excel — программа НОРМА (Rate). Однако эта про­грамма не позволяет определить ставку для переменных и не­прерывных рент, в связи с чем для решения задачи следует прибегнуть к методу Ньютона—Рафсона или методу секущей (см. Математическое приложение к гл. 6). Что касается обще­го потока платежей, то в пакете Excel имеется программа рас­чета ставки для произвольного потока с равными интервалами между платежами постнумерандо. Эту программу мы приме­ним в гл. 12 при расчете внутренней нормы доходности ВНДОХ (IRR).

В методических целях, вероятно, целесообразно начать с линейной интерполяции. По заданным R и 5, или R и А, на­ходят значения коэффициентов наращения или приведения ренты:

s_n;i=S/R; а_пи = А/Я.

Для оценки / применяется следующая интерполяционная формула:

/=//+ ^Vjifr-fr (5.38)

где a_dи a_i— табличные значения коэффициентов наращения или приведения рент для верхнего и нижнего уровня ставок (/^ /,), а — значение коэффициента наращения или приведения, для которого определяется размер ставки.

На рис. 5.3 и 5.4 изображены зависимости соответствующих коэффициентов от размера процентной ставки, а также интер­поляционные оценки и точные ее значения. Первые обозначе­ны как /, вторые как /".

Как видно из рисунков, оценки размера процентной ставки несколько отличаются от точных значений этой величины, при­чем, если за основу взят коэффициент приведения, то оценка оказывается завышенной. В свою очередь оценка / по коэффи-

117













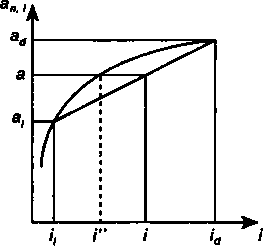
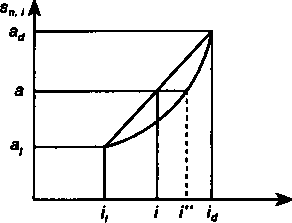
Рис. 5.3

Рис. 5.4

циенту наращения меньше точного значения. Чем меньше диа­пазон /_;+ /^ тем точнее оценка процентной ставки.

Применим теперь для расчета ставки программу НОРМА (Rate) пакета Excel.

Последовательность действий при использовании программы НОРМА

1. 
   Вызвать: £, "финансовые функции", НОРМА.
   
2. 
   Ввести данные, характеризующие ренту: в строке Клер — число периодов,
   

в строке Выплата — размер члена ренты с отрицательным

знаком,

в строке НЗ — современную стоимость ренты (Aили

в строке ВС показать наращенную сумму ренты в конце ее

срока (S>Rn),

в строке Тип указать вид ренты: 0 — для ренты постнуме-

рандо и 1 — для ренты пренумерандо. Если вид ренты не

указывается, то расчет ведется для ренты постнумерандо.

После выполнения действий 1—2 в итоговой строке Значе­ние автоматически показывается расчетная величина ставки за период в виде десятичной дроби. После нажатия кнопки ОК эта величина показывается в процентах в выделенной ячейке таб­лицы Excel.

ПРИМЕР 5.16. Допустим, предполагается путем ежегодных взно­сов постнумерандо по 100 млн руб. в течение 7 лет создать фонд в размере 1 млрд руб. Какова должна быть годовая процентная ставка?

118

Определим исходный коэффициент наращения: s_7;/ = 1000/100 = = 10. Для начала предположим, что искомая процентная ставка на­ходится в интервале 11—12%. Для этих значений ставки находим коэффициенты наращения: a_d= s^g = 10,08901; a,= s_TU= 9,78327. Откуда

10 - 9,78327 ' = 0,11 + _4ЛМП£%< r.-,onr*-,(0,12 - 0,11) = 0,11709, 10,08901 - 9,78327

или 11,709%.

Проверка: по формуле (5.5) находим: s_7;11709 = 9,999. Таким образом, найденное значение ставки обеспечивает выполнение поставленных условий почти точно. Если точность ответа не уст­раивает, то следует сузить интервал между ставками /, и i_d.

Решим теперь эту же задачу, но с помощью Excel.

После вызова программы НОРМА вводим в окошко значения:

Кпер: 7,

Выплата: -100,

БС: 1000,

Тип: 0,

Ответ: 0,117121443.

§5.5. Наращенные суммы и современные стоимости других видов постоянных рент

Кратко рассмотрим методики расчета наращенных сумм и современных стоимостей для некоторых разновидностей дис­кретных постоянных рент. Постоянные ренты с непрерывным поступлением платежей рассматриваются в гл. 6.

Ренты пренумерандо и ренты с выплатами в середине периодов.

Напомним, что под рентой пренумерандо понимается рента с платежами в начале периодов. Легко понять, что каждый член такой ренты "работает" на один период больше, чем в ренте по-стнумерандо. Отсюда наращенная сумма ренты пренумерандо, обозначим ее здесь как 5, больше в (1 + /) раз аналогичной рен­ты постнумерандо:

S = 5(1 + 0. Коэффициент наращения годовой ренты пренумерандо

119

Аналогичным путем получим для годовой ренты с начисле­нием процентов т раз в году

5=5(1 +j/m)^m.

Для р-срочных рент, у которых т = 1 и т * р, получим:

5=5(1 + 04

5= 5(1 +j/m)^m/P.

Точно такая же зависимость наблюдается и между современ­ными стоимостями и коэффициентами приведения рент пост-нумерандо и пренумерандо:

А = А(1 + 0; d_n;i= a_n;i{\ + /) и т.д.

Важной для практики является рента с платежами в середи­не периодов. Например, в случаях, когда поступления от произ­водственных инвестиций распределяются более или менее рав­номерно, применение рент пренумерандо или постнумерандо для описания таких потоков может привести к некоторым сме­щениям в значении получаемых показателей. В таких ситуациях для уменьшения погрешности рекомендуется суммы поступле­ний за период относить к середине периодов. Наращенные сум­мы и современные стоимости таких рент находим умножением соответствующих обобщающих характеристик рент постнуме­рандо на множитель наращения за половину периода. Так, для современных стоимостей находим следующие соотношения:

А_{/2= А{\ + О¹/² при р = 1, т = 1,

А_1/2= А(\ + О¹'²' при р > 1, т = 1,

А_{/2= A(l +j/m)^m'²при р = 1, т > 1,

^А\/2 ⁼ Л(1 +j/m)^m/2pпри р > 1, т > 1.

ПРИМЕР 5.17. Определим поправочный множитель, необходи­мый для расчета современной стоимости ренты с платежами в середине периодов. Условия ренты постнумерандо: р = 12, т= 1, / = 10%. Искомый множитель 1,1¹'^2х12 = 1,00398.

120

Отложенные ренты. Начало выплат у отложенной (отсрочен­ной) ренты сдвинуто вперед относительно некоторого момента времени. Например, погашение задолженности планируется на­чать спустя обусловленный срок (льготный период). Очевидно, что сдвиг во времени никак не отражается на величине нара­щенной суммы. Иное дело современная стоимость ренты.

Пусть рента выплачивается спустя /лет после некоторого на­чального момента времени. Современная стоимость ренты на начало выплат (современная стоимость немедленной ренты) равна А. Современная стоимость на начало периода отсрочки в t лет очевидно равна дисконтированной на этот срок величине современной стоимости немедленной ренты. Для годовой рен­ты находим

_tA = Av* = Яа„.у,(5.40)

где _tA — современная стоимость отложенной на /лет ренты.

ПРИМЕР 5.18. Пусть в примере 5.9 рента выплачивается не сра­зу, а спустя 1,5 года после момента оценки. Современная стои­мость отложенной ренты составит

12,368 х 1.185"¹'⁵ = 9,588 млн руб.

Современная стоимость отложенной ренты используется при решении целого ряда задач, чаще всего в расчетах, связанных с выплатами различного рода накоплений. Для иллюстрации об­судим одну из подобных задач. Пусть годовая ограниченная рента постнумерандо делится во времени между двумя участни­ками (например, речь идет о передаче собственности). Рента имеет параметры: R, п. Условия деления: а) каждый участник получает 50% капитализированной стоимости ренты; б) рента выплачивается последовательно — сначала первому участнику, затем второму.

Решение задачи сводится к расчету срока получения ренты первым участником, обозначим его как п_{. В оставшийся срок деньги получает второй участник. Таким образом, первый уча­стник получает немедленную ренту, второй — отложенную. Из принятых условий деления ренты следует:

121

Учитывая, что п₂= п — л,, находим:

,-(и,р ■-с»)-'--¹,,,

/ /

После ряда преобразований получим

_ -1п{[1 + (1 + i)-»]/2}
^П{1п(1 + /)

Результат зависит только от общего срока ренты и процент­ной ставки, которая учитывается в расчете.

ПРИМЕР 5.19. Срок годовой ренты постнумерандо 10 лет, / = 20%. Пусть рента делится между двумя участниками на тех ус­ловиях, которые были выше приняты при выводе формулы. Тогда

Чп[(1 + 1,2¹⁰)/2] _{ОЛв4 0}
л« = " ■———- = 2,981 - 3 года.

¹ |П 1,2 ' oiUMct.

Доля второго участника — следующие 7 лет.

Вечная рента. Напомним, что под вечной рентой (perpetuity) понимается ряд платежей, количество которых не ограничено — теоретически она выплачивается в течение бесконечного числа лет. В практике иногда сталкиваются со случаями, когда есть смысл прибегнуть к такой абстракции, например, когда предполагается, что срок потока платежей очень большой и конкретно не оговаривается. Примером могут служить некото­рые виды облигаций (см. гл. 11).

Очевидно, что наращенная сумма вечной ренты равна беско­нечно большой величине. На первый взгляд представляется бессодержательным и определение современной стоимости та­кой ренты. Однако это далеко не так. Современная величина вечной ренты есть конечная величина, которая определяется весьма просто. Выше было показано (см. (5.15)), что при п -+ оо пределом для коэффициента приведения является а_ж.. = 1//. От­куда для вечной ренты находим

д. = у- <⁵-⁴¹>

122

Таким образом, современная стоимость вечной ренты зави­сит только от размера члена ренты и процентной ставки. Из (5.41) следует

R = AJ₉(5.42)

т.е. член вечной ренты равен проценту от ее капитализирован­ной стоимости.

Нетрудно убедиться в том, что отдаленные платежи оказыва­ют весьма малое влияние на величину коэффициента приведе­ния. С ростом п прирост этого показателя уменьшается (см. рис. 5.2). В силу сказанного при больших сроках ренты и высо­ком уровне ставки для определения современной стоимости можно воспользоваться формулой (5.41) без заметной потери точности. Например, для ограниченной ренты при / = 20%, п = 100 и R = 1 получим точное значение: А = 4,999999, а по формуле (5.41) находим А_х= 5.

Для других видов рент получим:

4.- _{р[(1+ 0}./,_ ,j при/>>1,«=1;

А_да = — при р = т > 1.

ПРИМЕР 5.20. Требуется выкупить вечную ренту, член которой равен 5 млн руб., выплачиваемых в конце каждого полугодия. Ка­питализированная стоимость такой ренты при условии, что для ее определения применена годовая ставка 25%, составит:

^А* ⁼ 2(1,25^- 1) ^{= 42,361 МЛН Руб}*

Рента с периодом платежей, превышающим год. В анализе производственных инвестиционных проектов иногда встреча­ются с рентами, члены которых выплачиваются с интервалами, превышающими год. Определим наращенную сумму и совре­менную стоимость таких рент.

Пусть г — временной интервал между двумя членами ренты, проценты начисляются раз в году. В этом случае современная стоимость первого платежа составит на начало ренты величину 7V^r, второго — 7V^2r, последнего члена — 7V, где Г— величи­на члена ренты, п — срок ренты, кратный г. Последователь-

123

ность дисконтированных платежей представляет собой геомет­рическую профессию с первым членом 7V^r, знаменателем v^rи числом членов п/r. Сумма членов такой прогрессии при усло­вии, что Г= 1, равна:

^{** - v—ггг - (i} _{+ /}^{y-i = v (5-43)}

Разумеется, указанное в формуле соотношение коэффициен­тов приведения и наращения можно использовать в случаях, когда г — целое число лет.

ПРИМЕР 5.21. Сравниваются два варианта строительства неко­торого объекта. Первый требует разовых вложений в сумме 6 млн руб. и капитального ремонта стоимостью 0,8 млн руб. каж­дые 5 лет. Для второго затраты на создание равны 7 млн руб., на капитальный ремонт — 0,4 млн руб. каждые 10 лет. Временной го­ризонт, учитываемый в расчете, — 50 лет.

Капитализированная сумма затрат при условии, что / = 10 %, оценивается для каждого варианта в следующих размерах:

А_А= 6 + ^№- = 7,3 млн руб.,

^S5;10

А₂= 7 + ^^ = 7,25 млн руб.

^S10;10

Таким образом, в финансовом отношении варианты оказыва­ются равноценными при принятом уровне процентной ставки. Чем ставка выше, тем меньше влияют на результат затраты на ремонт. Так, если сравнение производится при ставке 20%, то получим Л₁ = 6,39, А₂= 7,05.

Переменная процентная ставка. На практике иногда сталки­ваются с потоками платежей, предполагающих применение пе­ременных во времени процентных ставок, например, при рест­руктурировании задолженности. Так, в последнем случае для облегчения положения должника применяются низкие ставки в первые годы выплат процентных платежей и более высокие в последующие (см. § 9.5).

Изменения размеров ставок могут быть какими угодно. Ес­ли же эти изменения "ступенчатые", то при определении нара­щенной суммы и современной стоимости постоянной ренты резонно применить стандартные формулы. Пусть для постоян-

124

ной ренты постнумерандо со сроком 10 лет предусматриваются два уровня процентной ставки, применяемые по пятилетиям. В этом случае

А - Ra_s._A+ *fl_5;/2(l + /|) •

ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА

1. 
   Четыркин ЕМ. Методы финансовых и коммерческих расчетов. М.: Дело, 1995. Гл. 4, 5.
   
2. 
   Четыркин Е.М., Васильева Н.Е. Финансово-экономические расчеты. М.: Фи­нансы и статистика, 1990. Гл. 3, 4.
   
3. 
   Cartledge P. Financial arithmetic. A practitioners guide. Euromoney Books, 1993.