Е. М. Четыркин финансовая математика

• Название: Е. М. Четыркин финансовая математика
• Анкор: chetyrkin_e_m_finansovaya_matematika.doc
• Дата: 22.04.2017
• Размер: 4.63 Mb.
• Имя файла: chetyrkin_e_m_finansovaya_matematika.doc
• Тип: Учебник; #4971
• страница: 4 из 58

§2.3. Наращение процентов в потребительском кредите

В потребительском кредите проценты, как правило, начис­ляются на всю сумму кредита и присоединяются к основ­ному долгу уже в момент открытия кредита (flatrateofinterest, add-oninterest). Условие, прямо скажем, весьма жесткое для должника.

Погашение долга с процентами производится частями, обычно равными суммами на протяжении всего срока кредита. Из сказанного следует, что наращенная сумма долга равна

5= Р(\ + ш), а величина разового погасительного платежа составит

/? = "£-, (2.10)

пт

где п — срок кредита в годах, т — число платежей в году.

В связи с тем что проценты здесь начисляются на первона­чальную сумму долга, а его фактическая величина систематиче­ски уменьшается во времени, действительная стоимость креди­та заметно превышает договорную процентную ставку. Подроб­нее об этом см. гл. 9, в которой, кроме того, обсуждается про­блема разбиения платежей на проценты и суммы погашения ос­новного долга. Необходимость в таком разбиении возникает при досрочном погашении задолженности.

ПРИМЕР 2.8. Кредит для покупки товара на сумму 1млн руб. от­крыт на три года, процентная ставка — 15% годовых, выплаты в конце каждого месяца. Сумма долга с процентами

S = 1(1 + 3 х 0,15) = 1,45 млн руб.

Ежемесячные платежи:

1450 Я = ₃'^₂ = 40,278 тыс. руб.

30

§2.4. Дисконтирование

по простым процентным ставкам.

Наращение по учетной ставке

В финансовой практике часто сталкиваются с задачей, об­ратной наращению процентов: по заданной сумме S, которую следует уплатить через некоторое время п, необходимо опреде­лить сумму полученной ссуды Р. Такая ситуация может возник­нуть, например, при разработке условий контракта. Расчет Р по Sнеобходим и тогда, когда проценты с суммы Sудерживаются вперед, т.е. непосредственно при выдаче кредита, ссуды. В этих случаях говорят, что сумма S дисконтируется или учитывается, сам процесс начисления процентов и их удержание называют учетом, а удержанные проценты — дисконтом (discount) или скидкой. Необходимость дисконтирования возникает, напри­мер, при покупке краткосрочных обязательств, оплата которых должником произойдет в будущем.

Термин "дисконтирование" употребляется и в более широ­ком смысле — как средство определения любой стоимостной величины, относящейся к будущему, на более ранний момент времени. Такой прием часто называют приведением стоимостно­го показателя к некоторому, обычно начальному, моменту вре­мени. (Приведение может быть осуществлено на любой, в том числе промежуточный, момент времени.)

Величину Р, найденную с помощью дисконтирования, назы­вают современной стоимостью, или современной величиной (pre­sentvalue), будущего платежа S, а иногда — текущей, или капи­тализированной, стоимостью. Современная величина суммы де­нег является одним из важнейших понятий в количественном анализе финансовых операций. В большинстве случаев именно с помощью дисконтирования, а не наращения, удобно учиты­вать такой фактор, как время. Как будет показано далее, боль­шинство аналитических методов основывается на определении современной величины платежей.

В зависимости от вида процентной ставки применяют два метода дисконтирования — математическое дисконтирование и банковский (коммерческий) учет. В первом случае применяется ставка наращения, во втором — учетная ставка.

Математическое дисконтирование. Математическое дискон­тирование представляет собой решение задачи, обратной нара­щению первоначальной суммы ссуды. Задача в этом случае

31

формулируется так: какую первоначальную сумму ссуды надо выдать в долг, чтобы получить в конце срока сумму S, при ус­ловии, что на долг начисляются проценты по ставке /? Решив (2.1) относительно Р, находим

'-ТТы- ⁽²">

Напомним, что п = t/K — срок ссуды в годах.

Установленная таким путем величина Р является современ­ной величиной суммы S, которая будет выплачена спустя п лет. Дробь 1/(1 + ni) называют дисконтным, или дисконтирующим, множителем. Этот множитель показывает, какую долю состав­ляет первоначальная величина долга в окончательной его сумме.

ПРИМЕР 2.9. Через 180 дней после подписания договора долж­ник уплатит 310 тыс. руб. Кредит выдан под 16% годовых. Какова первоначальная сумма долга при условии, что временная база равна 365 дням? Согласно (2.11) находим

р₌ 310000 ₌ 287328,59 руб.

Разность S — Р можно рассматривать не только как процен­ты, начисленные на Р, но и как дисконт с суммы S.

Банковский учет (учет векселей). Суть операции заключается в следующем. Банк или другое финансовое учреждение до на­ступления срока платежа (dateofmaturity) по векселю или ино­му платежному обязательству приобретает его у владельца по цене, которая меньше суммы, указанной на векселе, т.е. поку­пает (учитывает) его с дисконтом. Получив при наступлении срока векселя деньги, банк реализует процентный доход в виде дисконта. В свою очередь владелец векселя с помощью его уче­та имеет возможность получить деньги хотя и не в полном объ­еме, однако ранее указанного на нем срока.

При учете векселя применяется банковский, или коммерче­ский, учет. Согласно этому методу проценты за пользование ссудой в виде дисконта начисляются на сумму, подлежащую уп­лате в конце срока (maturityvalue). При этом применяется учет­ная ставка d.

32

Размер дисконта, или суммы учета, очевидно равен Snd; ес­ли d— годовая учетная ставка, то п измеряется в годах. Таким образом,

Р= S- Snd= S(l- nd),(2,12)

где п — срок от момента учета до даты погашения векселя.

Дисконтный множитель здесь равен (1 — nd). Из формулы (2.12) вытекает, что при п > \/dвеличина дисконтного множи­теля и, следовательно, суммы Р станет отрицательной. Иначе говоря, при относительно большом сроке векселя учет может привести к нулевой или даже отрицательной сумме Р, что ли­шено смысла. Например, при d= 20% уже пятилетний срок до­статочен для того, чтобы владелец векселя ничего не получил при его учете.

Учет посредством учетной ставки чаще всего осуществляет­ся при временной базе К = 360 дней, число дней ссуды обычно берется точным, АСТ/360.

ПРИМЕР 2.10. Тратта (переводной вексель) выдан на сумму 1 млн руб. с уплатой 17.11.2000. Владелец векселя учел его в банке 23.09.2000 по учетной ставке 20% (АСТ/360). Оставшийся до конца срока период равен 55 дням. Полученная при учете сум­ма (без уплаты комиссионных) равна

Р= 1000000(1 - -^Цг 0,2) = 969444,4 руб.

Дисконт составит 30555,6 руб.

Дополним условия примера. Пусть на всю сумму долга теперь начисляются проценты по ставке простых процентов / = 20,5% го­довых. В этом случае, очевидно, надо решить две задачи: опре­делить наращенную сумму долга и сумму, получаемую при учете. Оба последовательных действия можно представить в одной фор­муле

Р" = Р(1 + л/)(1 -n'd),

где п— общий срок обязательства, п' — срок от момента учета до погашения.

Пусть в данном примере п= 120/360, тогда

Р" = 1 000 000(1 + -^=£- 0,205)(1 - -^г 0,2) = 1 035 690 руб.
Зои Зои

33

Разумеется, дисконт, как скидка с конечной суммы долга, необязательно определяется через ту или иную процентную ставку, он может быть установлен по соглашению сторон и в виде фиксированной величины для всего срока. Однако, размер ставки неявно всегда имеется ввиду.

Наращение по учетной ставке. Простая учетная ставка иногда применяется и при расчете наращенной суммы. В частности, в этом возникает необходимость при определении суммы, кото­рую надо проставить в векселе, если задана текущая сумма дол­га. Наращенная сумма в этом случае

Множитель наращения здесь равен 1/(1 — nd). Наращение не пропорционально ни сроку, ни ставке. Заметим, что при п> \/dрасчет лишен смысла, так как наращенная сумма становится бесконечно большим числом. Такая ситуация не возникает при математическом дисконтировании: при любом сроке современ­ная величина платежа больше нуля.

ПРИМЕР 2.11. По данным примера 2.2 определим наращенную сумму при условии, что проценты начисляются по простой учет­ной ставке d= 18%:

S = 1 000 000 — = 1148105,62 руб.

1 -Ц|0,18 360

§2.5. Прямые и обратные задачи

при начислении процентов

и дисконтировании по простым ставкам

Как было показано выше, оба вида ставок (наращения и дисконтирования) применяются для решения сходных задач. Однако для ставки наращения прямой задачей является опреде­ление наращенной суммы, обратной — дисконтирование. Для учетной ставки, наоборот, прямая задача заключается в дискон­тировании, обратная — в наращении.

Очевидно, что рассмотренные два метода наращения и дис­контирования — по ставке наращения / и учетной ставке d— приводят к разным результатам даже тогда, когда / = d.

34

Ставки	Прямая задача	Обратная задача	Формулы
d	S= Р(\ + ni) Р= S(l - nd)	Р =5/(1 + ni) S= PI (I nd)	см. (2.1), (2.11) см. (2.12), (2.13)

Заметим, что учетная ставка отражает фактор времени более жестко. Влияние этого фактора усиливается при увеличении ве­личины ставки. Для иллюстрации сказанного на рис.2.5 и в табл. 2.1 приведены дисконтные множители (ДМ) для случая, когда / = d = 20%.

ДМ ^	,
1
		/
0,833		^d
0,8			->

Рис. 2.5

Таблица 2.1

Дисконтные множители, i - d » 20%

Вид			Срок в годах
ставки	1/12	1/4	1/2	1	2	10
/ d	0,9836 0,9833	0,9524 0,9500	0,9091 0,9000	0,8333 0,8000	0,7143 0,6000	0,3333

Рис. 2.6

Сравнивая формулы (2.1) и (2. 13), легко понять, что учет­ная ставка дает более быстрый рост суммы задолженности, чем такой же величины ставка наращения. Множители наращения (МН) для двух видов ставок при условии, что / = d= 20%, по­казаны на рис. 2.6 и в табл. 2.2.



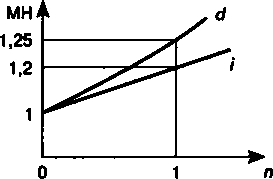
35

Таблица 2.2

	Множители		наращения,	/ = d = 20%
Вид	Срок в годах
ставки	1/12	1/4	1/2	1	2	10
d	1,0167 1,0169	1,0500 1,0526	1,1000 1,1111	1,2000 1,2500	1,4000 1,6667	3 00

Из сказанного выше следует, что выбор конкретного вида процентной ставки заметно влияет на финансовые итоги опе­рации. Однако возможен такой подбор величин ставок, при котором результаты наращения или дисконтирования будут одинаковыми. Такие ставки называются эквивалентными. Проблема эквивалентности процентных ставок рассматривает­ся в гл. 3.

§2.6. Определение срока ссуды и величины процентной ставки

При разработке условий контрактов или их анализе и срав­нении возникает необходимость в решении ряда, если так мож­но назвать, вторичных задач — определении срока ссуды и раз­мера процентной ставки в том или ином ее виде при всех про­чих заданных условиях.

Срок ссуды. Необходимые для расчета продолжительности ссуды в годах и днях формулы получим, решив (2.1) и (2.12) от­носительно п.

Срок в годах:

„ S- Р- S/ Р- 1
Pii

(2.14)


за)

(2.15)

_ S-Р„ 1 -Р/S

Sd d

Срок в днях (напомним, что п = t/K, где К — временная ба-

«- S-P


К

Pi
(2.16)


' Sd^К

(2.17)

36

ПРИМЕР 2.12. Какова должна быть продолжительность ссуды в днях для того, чтобы долг, равный 100 тыс. руб., вырос до 120 тыс. руб. при условии, что начисляются простые проценты по ставке 25% годовых (ACT/ACT)? По формуле (2.16) находим

(= 120-100 365 = 292 дня.
100 х 0.25 ^Д

Величина процентной ставки. Необходимость в расчете про­центной ставки возникает при определении финансовой эффе­ктивности операции и при сравнении контрактов по их доход­ности в случаях, когда процентные ставки в явном виде не ука­заны. Решив выражения (2.1) и (2.12) относительно / или d, по­лучим искомые формулы для сроков, измеренных в годах и

днях:

i'-^T'-^jr¹¹'<sup>(218)

d</sup>_-¹_%r-^A_ir^K_<^2|9_>

ПРИМЕР 2.13. В контракте предусматривается погашение обяза­тельства в сумме 110 тыс. руб. через 120 дней. Первоначальная сумма долга 90 тыс. руб. (АСТ/360). Как видим, здесь не огово­рен уровень процентной ставки. Необходимо определить доход­ность ссудной операции для кредитора в виде ставки процента и учетной ставки. По формулам (2.18) и (2.19) находим

' = ll°^on³⁶Q = 0,666(6), или 66,67%, 90 х 120

d= Л!?"^360 = 0,5454, или 54,54%. 110 х 120

Иногда размер дисконта фиксируется в договоре в виде про­цента скидки (общей учетной ставки) d' за весь срок ссуды. В этом случае

Р= 5(1 - d').

Имея в виду, что Р = S / (1 + /и), находим

37

d' i=

Годовая учетная ставка находится элементарно:

d=d' I n.

ПРИМЕР 2.14. Стороны договорились о том, что из суммы ссу­ды, выданной на 210 дней, удерживается дисконт в размере 12%. Необходимо определить цену кредита в виде годовой ставки про­стых процентов и учетной ставки {К= 360):

/ = _oin °'¹² = 0,23376, или 23,38%,

^-И -0,12) 360

^d= o^lL» ⁼ 0,20571, или 20,57%. 210/360

§ 2.7. Конверсия валюты и наращение процентов

Рассмотренные выше методы наращения процентов позво­ляют перейти к обсуждению более сложных и важных в прак­тическом отношении задач. Остановимся на одной из них. Речь пойдет о совмещении операций конверсии (обмена) валюты и наращения процентов.

При возможности обмена рублевых средств на СКВ и обрат­ной конверсии целесообразно сравнить доходы от непосредст­венного размещения имеющихся денежных средств в депозиты и опосредованно через другую валюту. Сказанное относится и к получению дохода от СКВ при ее обмене на рубли, депони­ровании и обратной конверсии.

Возможны четыре варианта для наращения процентов с кон­версией денежных ресурсов и без нее:

без конверсии: СКВ -* СКВ;

с конверсией: СКВ — Руб — Руб — СКВ;

без конверсии: Руб -* Руб;

с конверсией: Руб — СКВ — СКВ — Руб.

Варианты с конверсией показаны на рис.2.7.

38

Р(СКВ) /. S(CKB) Р(руб.) /. S(py6.)

_{I , t * , t}

Р(руб.) *-► S(py6.) P(CKB) '-+> S(CKB)

а б

Рис. 2.7

В операции наращения с конверсией валют существует два источника дохода — изменение курса и наращение процентов, причем, если второй из них безусловный (так как ставка про­цента фиксирована), то этого нельзя сказать о первом источни­ке. Более того, двойное конвертирование валюты (в начале и конце операции) может быть при неблагоприятных условиях убыточным. Решим в связи с этим две задачи. Определим сум­му в конце операции и ее доходность для двух вариантов опе­рации с конверсией.

Вариант СКВ -* Руб -* Руб -* СКВ. Проанализируем сначала вариант я, показанный на рис. 2.7. Примем обозначения:

P_v— сумма депозита в СКВ,

Р_г— сумма депозита в рублях,

S_v— наращенная сумма в СКВ,

S_r— наращенная сумма в рублях,

А^ — курс обмена в начале операции (курс СКВ в рублях),

К_{— курс обмена в конце операции,

п — срок депозита,

/ — ставка наращения для рублевых сумм,

j— ставка наращения для конкретного вида СКВ.

Операция предполагает три шага: обмен валюты на рубли, наращение процентов на эту сумму и, наконец, конвертирова­ние в исходную валюту. Конечная (наращенная) сумма в валю­те определяется как

S_v= />Л (1 + ni) -jL. (2.20)

Три сомножителя этой формулы соответствуют трем пере­численным выше шагам. Множитель наращения т с учетом двойного конвертирования здесь имеет вид

_m = A_(1+m)=J_^. ₍2.21)

39

Взаимодействие двух факторов роста исходной суммы в этой формуле представлено наиболее наглядно. С ростом ставки множитель наращения линейно увеличивается, в свою очередь, рост конечного курса обмена уменьшает его.

ПРИМЕР 2.15. Предполагается поместить 1000 долл. на рубле­вом депозите. Курс продажи на начало срока депозита 26,08 руб. за $1, курс покупки доллара в конце операции 26,45 руб. Про­центные ставки: / = 22%; у = 15% (360/360). Срок депозита — 3 месяца.

26,08 з 22

S„ = Ю00 х -^Г(1 + -£- _х ^) _{= 104}0,2 долл.

—■—(1 + — х -==-* = 26,45 ^v 12 100

В свою очередь прямое наращение исходной долларовой сум­мы по долларовой ставке процента дает

S_v= 1000(1 + 0,25 х 0,15) = 1037,5 долл.

Продолжим анализ и поставим перед собой вторую задачу — измерим доходность операции в целом. В качестве измерителя доходности за срок операции примем простую годовую ставку процента /_э. Эта ставка характеризует рост суммы P_vдо величи­ны 5_V:

S -Р

э

/ = у у

Л/»

Подставим в эту формулу значение S_v, полученное из (2.20). После несложных преобразований имеем

'э =

-§41 + Л0 " 1 ^А1

, т — 1

/^{Л =} —::—

Данное выражение позволяет сделать ряд заключений, кото­рые удобно получить, обратившись к графику (см. рис. 2.8). Введем величину, характеризующую отношение последнего и первого курсов валюты:

* = А

^v

С увеличением к эффективность операции падает. При к = 1 параметр /_э = /, при к > 1 параметр /_э < / (точка а на оси к), на­конец, при самой благоприятной для владельца денег ситуации (к < 1) имеем /_ > /.

40

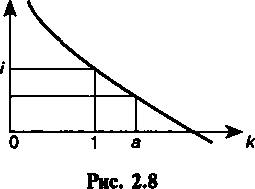
Вариант Руб -* СКВ -* СКВ -* Руб. В этом варианте (см. рис. 2.7, б) трем шагам операции соответствуют три сомножителя формулы

5_Г= A(i + _nj)K_x= Р_г{\ + _Лу)А

(2.22)

Как и в предыдущем варианте, множитель наращения ли­нейно зависит от ставки, но теперь ставки процента для СКВ. Очевидно, что зависимости этого множителя от конечного кур­са или его темпа роста также линейные.

ПРИМЕР 2.16. Допустим, необходимо поместить на валютном депозите сумму в рублях (1 млн). Остальные условия — из приме­ра 2.15. Наращенная сумма в рублях к концу срока составит:

26 45 S, = 1000 х (1 + 0,25 х 0,15)-^^- = 1052,2 тыс. руб.

20,Оо

Прямое инвестирование в рублевый депозит дает больше: S_r= 1000 х (1 + 0,25 х 0,22) = 1055 тыс. руб.

Перейдем теперь к анализу эффективности операции. До­ходность операции определяется как

откуда

S- Р '^э Р_гп '


-(*<•

+ nj) - 1 \/п = (*(1 + nj) - \)/n. (2.23)

41

Зависимость показателя эффективности от к, как видим, ли­нейная. При к = 1 /_э =j(см. рис. 2.9), при £ > 1 /_э >у , нако­нец, при Л < 1 /_э <у, в частности, если к = к' = \/(\ + лу), опе­рация не принесет никакого дохода: /_э < 0.

'.А

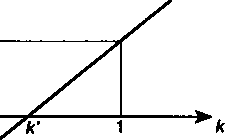
У

Рис. 2.9

ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА

1. 
   Башарин Г. П. Начала финансовой математики. М.: ИНФРА-М, 1997.
   
2. 
   Четыркин Е.М., Васильева Н. Е. Финансово-экономические расчеты. М.: Фи­нансы и статистика, 1990. Гл. 1.
   
3. 
   Ковалев В.В., Уланов В.А. Курс финансовых вычислений. М.: Финансы и ста­тистика, 1994. Гл. 5.
   
4. 
   Cartledge P. Financial arithmetic. A practitioners guide. Euromoney Books, 1993.
   

Глава 3 СЛОЖНЫЕ ПРОЦЕНТЫ

§3.1. Начисление сложных годовых процентов

Формула наращения. В средне- и долгосрочных финансово-кредитных операциях, если проценты не выплачиваются сразу после их начисления, а присоединяются к сумме долга, приме­няют сложные проценты (compoundinterest). База для начисления сложных процентов в отличие от простых не остается постоян­ной — она увеличивается с каждым шагом во времени. Абсо­лютная сумма начисляемых процентов возрастает, и процесс увеличения суммы долга происходит с ускорением. Наращение по сложным процентам можно представить как последователь­ное реинвестирование средств, вложенных под простые про­центы на один период начисления {runningperiod). Присоедине­ние начисленных процентов к сумме, которая послужила базой для их начисления, часто называют капитализацией процентов.

Найдем формулу для расчета наращенной суммы при усло­вии, что проценты начисляются и капитализируются один раз в году (годовые проценты). Для этого применяется сложная став-ка наращения. Для записи формулы наращения применим те же обозначения, что и в формуле наращения по простым про­центам:

Р — первоначальный размер долга (ссуды, кредита, капита­ла и т.д.),

S — наращенная сумма на конец срока ссуды,

п — срок, число лет наращения,

/ — уровень годовой ставки процентов, представленный де­сятичной дробью.

Очевидно, что в конце первого года проценты равны вели­чине Pi, а наращенная сумма составит Р + Pi= Р(\ + /). К кон­цу второго года она достигнет величины Р(\ + /) + Р(1 + /)/' = = Р(\ + О² и т.д. В конце л-го года наращенная сумма будет равна

43

S= P(\ + i)ⁿ.

(3.1)

Проценты за этот же срок в целом таковы:

/= S- Р = P[(l+ i)ⁿ- 1]. (3.2)