Е. М. Четыркин финансовая математика

• Название: Е. М. Четыркин финансовая математика
• Анкор: chetyrkin_e_m_finansovaya_matematika.doc
• Дата: 22.04.2017
• Размер: 4.63 Mb.
• Имя файла: chetyrkin_e_m_finansovaya_matematika.doc
• Тип: Учебник; #4971
• страница: 3 из 58

Глава 2

НАРАЩЕНИЕ И ДИСКОНТИРОВАНИЕ

ПО ПРОСТЫМ

ПРОЦЕНТНЫМ СТАВКАМ

§2.1. Формула наращения

Под наращенной суммой ссуды (долга, депозита, других видов выданных в долг или инвестированных денег) понимают перво­начальную ее сумму с начисленными процентами к концу сро­ка начисления (dateofmaturity, duedate). Наращенная сумма оп­ределяется умножением первоначальной суммы долга (principal) на множитель наращения, который показывает, во сколько раз наращенная сумма больше первоначальной. Расчетная формула зависит от вида применяемой процентной ставки и условий на­ращения.

К наращению по простым процентам обычно прибегают при выдаче краткосрочных ссуд (на срок до 1 года) или в случаях, когда проценты не присоединяются к сумме долга, а периоди­чески выплачиваются. Для записи формулы наращения про­стых процентов (simpleinterest) примем обозначения:

/ — проценты за весь срок ссуды;

Р — первоначальная сумма долга;

S— наращенная сумма, т. е. сумма в конце срока;

/ — ставка наращения процентов (десятичная дробь);

п — срок ссуды.

Если срок измеряется в годах (как это обычно и бывает), то I означает годовую процентную ставку. Соответственно каждый год приносит проценты в сумме А". Начисленные за весь срок проценты составят

/ = Pni. Наращенная сумма, таким образом, находится как

S= Р + / = Р + Pni= />(1 + #10. (2.1)

20

Выражение (2.1) называют формулой наращения по простым процентам или кратко — формулой простых процентов, а мно­житель (1 + ni) — множителем наращения простых процентов. График роста по простым процентам представлен на рис. 2.1.

Заметим, что увеличение процентной ставки или срока в к раз одинаковым образом влияет на множитель наращения. Последний увеличится в (1 + kni) / (1 + ni) раз.

S)	\			S
				Pni
р
				—►

1 2

Рис. 2.1

ПРИМЕР 2.1. Определим проценты и сумму накопленного долга, если ссуда равна 700 тыс.руб., срок 4 года, проценты простые по ставке 20% годовых (/ = 0,2):

/ = 700 х 4 х 0,2 = 560 тыс. руб.;

S = 700 + 560 = 1260 тыс. руб.

Увеличим теперь ставку в два раза. Сумма процентов при этом, естественно, удвоится. Однако наращенная сумма увеличится в

(1 + 2 х 4 х 0,2) / (1 + 4 х 0,2) = 1,444 раза.

Практика расчета процентов для краткосрочных ссуд. Пос­кольку процентная ставка, как правило, устанавливается в рас­чете за год, то при сроке ссуды менее года необходимо опреде­лить, какая часть годового процента уплачивается кредитору. Аналогичная проблема возникает и в случаях, когда срок ссуды меньше периода начисления.

Рассмотрим наиболее распространенный в практике случай — с годовыми периодами начисления. Очевидно, что срок ссу­ды необязательно равен целому числу лет. Выразим срок п в ви­де дроби

21

п = -£, (2.2)

где / — число дней ссуды, К — число дней в году, или времен­ная база начисления процентов (timebasis).

При расчете процентов применяют две временные базы: К = 360 дней (12 месяцев по 30 дней) или К= 365, 366 дней. Если К = 360, то получают обыкновенные или коммерческие про­центы (ordinaryinterest), а при использовании действительной продолжительности года (365, 366 дней) рассчитывают точные проценты (exactinterest) .

Число дней ссуды также можно измерить приближенно и точно. В первом случае продолжительность ссуды определяется из условия, согласно которому любой месяц принимается рав­ным 30 дням. В свою очередь точное число дней ссуды опреде­ляется путем подсчета числа дней между датой выдачи ссуды и датой ее погашения. День выдачи и день погашения считаются за один день. Точное число дней между двумя датами можно определить по табл. 1 Приложения.

Итак, возможны и применяются на практике три варианта расчета простых процентов.

1. 
   Точные проценты с точным числом дней ссуды. Этот вари­ант, естественно, дает самые точные результаты. Данный спо­соб применяется центральными банками многих стран и круп­ными коммерческими банками, например, в Великобритании, США. В коммерческих документах он обозначается как 365/365 или ACT/ACT.
   
2. 
   Обыкновенные проценты с точным числом дней ссуды. Этот метод, иногда называемый банковским (Banker'sRule), распро­странен в межстрановых ссудных операциях коммерческих банков, во внутристрановых — во Франции, Бельгии, Швейца­рии. Он обозначается, как 365/360 или АСТ/360. Этот вариант дает несколько больший результат, чем применение точных процентов. Заметим, что при числе дней ссуды, превышающем 360, данный способ приводит к тому, что сумма начисленных процентов будет больше, чем предусматривается годовой став­кой. Например, если / = 364, то/? = 364/360 = 1,01111. Мно­житель наращения за год при условии, что / = 20% , составит 1,20222.
   
3. 
   Обыкновенные проценты с приближенным числом дней ссуды. Такой метод применяется тогда, когда не требуется большой точности, например при промежуточных расчетах. Он принят в
   

22

практике коммерческих банков Германии, Швеции, Дании. Метод условно обозначается как 360/360.

Очевидно, что вариант расчета с точными процентами и приближенным числом дней ссуды лишен смысла и не приме­няется.

Поскольку точное число дней ссуды в большинстве случаев, но разумеется, не всегда, больше приближенного (в чем легко убедиться, определив среднее за год число дней в месяце, кото­рое равно 30,58), то метод начисления процентов с точным чис­лом дней ссуды обычно дает больший рост, чем с приближен­ным.

ПРИМЕР 2.2. Ссуда в размере 1 млн руб. выдана 20.01 до 05.10 включительно под 18% годовых. Какую сумму должен за­платить должник в конце срока при начислении простых процен­тов? При решении применим все три метода. Предварительно определим число дней ссуды: точное — 258, приближенное — 255.

1. Точные проценты с точным числом дней ссуды (365/365):

S = 1 000 000(1 + -fif-0,18) = 1 127 233 руб. 365

2. Обыкновенные проценты с точным числом дней ссуды
(360/365):

S = 1 000 000(1 + -||^-0.18) = 1 129 000 руб. ооО

3. Обыкновенные проценты с приближенным числом дней ссу­
ды (360/360):

25*5 S = 1 000 000(1 + —Ц-0,18) = 1 127 500 руб.

Если общий срок ссуды захватывает два смежных календар­ных года и есть необходимость в делении суммы процентов ме­жду ними (например, при определении годовых сумм дохода и т.д.), то общая сумма начисленных простых процентов составит сумму процентов, полученных в каждом году:

/ = /j + /₂ = Pn_xi+ Pn₂i,

здесь tijи п₂— части срока ссуды, приходящиеся на каждый ка­лендарный год.

23

Переменные ставки. В кредитных соглашениях иногда пред­усматриваются изменяющиеся во времени процентные ставки. Если это простые ставки, то наращенная на конец срока сумма определяется следующим образом:

S= Р[\ + л,/, + л₂/₂+-.+*«'«) - W^{1 +} 2 "'Ч' <²-³>

где /, — ставка простых процентов в периоде /, n_t— продолжи­тельность периода с постоянной ставкой, п = Z /?,.

ПРИМЕР 2.3. Контракт предусматривает следующий порядок на­числения процентов: первый год — 16%, в каждом последующем полугодии ставка повышается на 1%. Необходимо определить множитель наращения за 2,5 года. Находим

1 + 2п^ = 1 + 1 х 0,16 + 0,5 х 0,17 + 0,5 х 0,18 +

+ 0,5 х0,19 = 1,43.

Начисление процентов при изменении сумм депозита во време­ни. Принципиально ничего не меняется, если сумма, на кото­рую начисляются проценты, изменяет свою величину во време­ни (размер вклада на сберегательном счете, текущий счет при периодическом его пополнении или снятии денег и т.п.). В этом случае

/ = 2 Л/1/, (2.4)

где Rj— остаток средств на счете в момент jпосле очередного поступления или списания средств, /?. — срок хранения денег (в годах) до нового изменения остатка средств на счете.

В банковско-сберегательном деле обычно применяют следу­ющий способ, основанный на преобразовании (2.4). Для этого измерим интервалы между моментами изменений величины ос­татка на счете в днях, а процентную ставку выразим в процен­тах (а не в десятичных дробях как выше). После чего получим

/- уяп.1ш2*&:*-.(2.5)

у ^JJloo i^к'

24

Как и прежде К означает число дней в году, a tj— срок в днях между последовательными изменениями остатков на счете.

Величину ЛRjt_}/100 называют процентным числом (interestnumber), а делитель — процентным (или постоянным) делителем (interestdivisor).

ПРИМЕР 2.4. Движение средств на счете характеризуется следую­щими данными: 05.02 поступило 12 млн руб., 10.07 снято 4 млн руб. и 20.10 поступило 8 млн руб. Найти сумму на счете на конец года. Процентная ставка 18% годовых.

Процентный делитель составит 365 : 18 = 20,27778. Расчет суммы процентных чисел приведен в следующей таблице.

Дата	Движение средств	Остаток {Rj)	Срок Ц)	Процентное число
05.02	12	12	155	18,6
10.07	-4	8	102	8,16
20.10	8	16	72	11,52
31.12	—	16	—	—-
Итого				38,28

Сумма процентов за весь срок равна ₉Т77я ^{= 1} *®®® ^{млн ру}^'

Реинвестирование по простым ставкам. В практике при инве­стировании средств в краткосрочные депозиты иногда прибега­ют к неоднократному последовательному повторению нараще­ния по простым процентам в пределах заданного общего срока. Фактически это означает реинвестирование средств, полученных на каждом этапе наращения, с помощью постоянной или пере­менной ставок. Наращенная сумма для всего срока составит в этом случае

5= (1 + Vi)0 + *₂У-0 + *А)-. <²-^б>

где i_t— размер ставок, по которым производится реинвестиро­вание.

Если промежуточные сроки начисления и ставки не изменя­ются во времени, то вместо (2.6) имеем

5= F\\ + *,)«, где т — количество повторений реинвестирования.

(2.7)

25

ПРИМЕР 2.5. 100 млн руб. положены 1-го марта на месячный де­позит под 20% годовых. Какова наращенная сумма, если опера­ция повторяется 3 раза?

Если начислять точные проценты (365/365), то

q-i пао*

^{5 = 100(1+}Ж⁰'^{2И1 +} збГ⁰'²⁾⁽¹⁺^°'^{2) =}

= 105,013 млн руб.

Начисление обыкновенных процентов (360/360) при реинве-стированиии дает

30 S = 100(1 + -zr0,2)³ = 105,084 млн руб.

§ 2.2. Погашение задолженности частями

Контур финансовой операции. Необходимым условием фи­нансовой или кредитной операции в любой ее форме является сбалансированность вложений и отдачи. Понятие сбалансиро­ванности удобно пояснить на графике (см. рис. 2.2). Выдана ссуда на срок Т в размере Р. На протяжении этого срока в счет погашения задолженности производятся, допустим, два плате­жа Л, и Я₂, а в конце срока выплачивается остаток задолженно­сти в сумме R₃(для нас здесь не имеет значения, какая часть этой суммы идет на выплату процентов, а какая — на погаше­ние долга). Очевидно, что на интервале /, задолженность воз­растает (в силу начисления процентов) до величины Р_{. В кон­це этого периода выплачивается в счет погашения задолженно­сти сумма Л,. Долг уменьшается до К_{и т.д. Заканчивается опе­рация получением кредитором в окончательный расчет суммы R_vВ этот момент задолженность должна быть равна нулю. На­зовем такой график контуром операции (рис. 2.2, б).

Сбалансированная операция обязательно имеет замкнутый контур. Иначе говоря, последняя выплата полностью покрыва­ет остаток задолженности. В этом случае совокупность плате­жей точно соответствует условиям сделки. Контур операции бу­дет применяться ниже в методических целях при анализе ряда финансовых операций.

Частичные платежи. Краткосрочные обязательства иногда погашаются с помощью ряда промежуточных платежей. В этом

26

р 1	гг. Но h	k
а	1 l	'

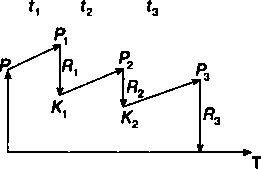Рис. 2.2

случае надо решить вопрос о том, какую сумму надо брать за базу для расчета процентов и каким путем определять остаток задолженности. Существуют два метода решения этой задачи. Первый, который применяется в основном в операциях со сро­ком более года, называют актуарным методом (Actuarialmethod). Второй метод назван правилом торговца (Merchant'sRule). Он используется коммерческими фирмами в сделках со сроком не более года. Если иное не оговорено, то при начислении про­центов в обоих методах используются обыкновенные проценты с приближенным числом дней (360/360).

Актуарный метод предполагает последовательное начисле­ние процентов на фактические суммы долга. Частичный платеж идет в первую очередь на погашение процентов, начисленных на дату платежа. Если величина платежа превышает сумму на­численных процентов, то разница (остаток) идет на погашение основной суммы долга. Непогашенным остаток долга служит базой для начисления процентов за следующий период и т.д. Если же частичный платеж меньше начисленных процентов, то никакие зачеты в сумме долга не делаются. Поступление при­плюсовывается к следующему платежу. Для случая, показанно­го на рис. 2.2, получим следующие расчетные формулы для оп­ределения остатка задолженности (К)

К_х- Р(\ + /,0 - Л,; К₂= *,20 - R_T

(2.8)

Задолженность на конец срока должна быть полностью по­гашена. Таким образом,

К₂(\ + /₃0 - Л, = 0.

27

ПРИМЕР 2.6. Имеется обязательство погасить за 1,5 года (с 12.03.1999 по 12.09.2000 г.) долг в сумме 15 млн руб. Креди­тор согласен получать частичные платежи. Проценты начисляют­ся по ставке 20% годовых. Частичные поступления характеризу­ются следующими данными (в тыс. руб.):

1999. 
      г.-500;
      
2000. 
      г.-5000; 30.06.2000 г. - 8000; 12.09.2000 г.-?
      

Решение представим в следующей последовательной записи:

12.03.1999 долг 12.06.1999 долг с процентами поступление

15 000

15 750

-500

(Поскольку поступившая сумма меньше начисленных процен-тов(750), то она присоединяется к следующему поступлению.)

12.06.2000 долг с процентами 18 750

поступления 500+5000 -5 500

Остаток долга 13 250

30.06.2000 долг с процентами 13 382,5

поступление 8000 -8 000

Остаток долга 5 382,5

12.09.2000 долг с процентами 5 597,8

Контур данной операции представлен на рис. 2.3.

15,75_

18,75

5,5 13,3825

V^l 5,5978

12.03.99

12.09.2000

Рис. 2.3

Иной подход предусматривается правилом торговца. Здесь возможны два варианта. Если срок ссуды не превышает год, то сумма долга с процентами остается неизменной до полного по­гашения. В свою очередь накапливаются частичные платежи с начисленными на них до конца срока процентами. Последний взнос должен быть равен разности этих сумм. В случае, когда срок превышает год, указанные выше расчеты делаются для го-

28

дового периода задолженности. В конце года из суммы задол­женности вычитается наращенная сумма накопленных частич­ных платежей. Остаток погашается в следующем году. Алгоритм можно записать следующим образом:

0=5- К= Р(1 +ш)-2Л,(1 + /)/,),

(2.9)

где Q— остаток долга на конец срока или года, S— наращен­ная сумма долга, К— наращенная сумма платежей, Л — сумма частичного платежа, п — общий срок ссуды, t— интервал вре­мени от момента платежа до конца срока ссуды или года.

Графическое изображение такой операции при выплате двух промежуточных платежей охватывает два параллельных контура (см. рис. 2.4). Первый характеризует наращение задолженности, второй — наращение на суммы поступлений.

Заметим, что для одних и тех же данных актуарный метод и правило торговца в общем случае дают разные результаты. Ос­таток задолженности по первому методу немного выше, чем по второму.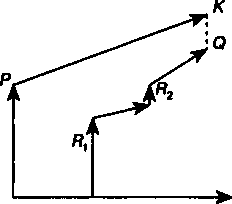



Рис. 2.4

ПРИМЕР 2.7. Обязательство (1,5 млн руб.), датированное 10.08.1999 г., должно быть погашено 10.06.2000 г. Ссуда выдана под 20% годовых. В счет погашения долга 10.12.1999 г. поступило 800 тыс. руб. Остаток долга на конец срока согласно (2.9) составит

О = 1,5(1 + ^?-0,2) - 0,8(1 + Г^-0,2) = 0,87 млн руб.

В свою очередь, при применении актуарного метода получим

О = [(1,5 + -^-0,2) - 0,8](1 + -^-0,2) = 0,88 млн руб.

29