Е. М. Четыркин финансовая математика

• Название: Е. М. Четыркин финансовая математика
• Анкор: chetyrkin_e_m_finansovaya_matematika.doc
• Дата: 22.04.2017
• Размер: 4.63 Mb.
• Имя файла: chetyrkin_e_m_finansovaya_matematika.doc
• Тип: Учебник; #4971
• страница: 6 из 58

Глава 4

ПРОИЗВОДНЫЕ

ПРОЦЕНТНЫЕ РАСЧЕТЫ.

КРИВЫЕ ДОХОДНОСТИ

§4.1. Средние процентные ставки

Если в финансовой операции размер процентной ставки из­меняется во времени, то все значения ставки можно обобщить с помощью средней. Замена всех усредняемых значений ставок на среднюю процентную ставку по определению не изменяет резуль-татов наращения или дисконтирования.

Начнем с простых ставок. Пусть за последовательные пери­оды л,, л₂,..., п_кначисляются простые проценты по ставкам /,, /₂,..., i_k. Искомые средние получим посредством приравнива­ния соответствующих множителей наращения друг к другу:

1 + N7= 1+2/1,/,.

Откуда

2/1,/,
''—JT'^(4л)

где N = Z/i, — общий срок наращения процентов.

Найденный показатель представляет собой среднюю ариф­метическую взвешенную с весами, равными продолжительно­сти отдельных периодов.

Аналогичным способом определим среднюю учетную ставку:

2лД

ПРИМЕР 4.1. Контракт предусматривает переменную по перио­дам ставку простых процентов: 20, 22 и 25 %. Продолжительность последовательных периодов начисления процентов: два, три и пять месяцев. Какой размер ставки приведет к аналогичному на­ращению исходной суммы? Находим среднюю ставку:

66

- 0,2 х 2 + 0,22 х 3 + 0,25 х 5

/ = — =0,231, или 23,1%.

Если усредняются сложные переменные во времени ставки сложных процентов, то из равенства множителей наращения

(iWf-lw/.niwJT'...

следует

/.ф₊/₁)^Л,(1 ₊ /₂)^Л2...-1. (4.3)

Средняя в этом случае вычисляется как взвешенная средняя геометрическая.

ПРИМЕР 4.2. Допустим, для первых двух лет ссуды применяется ставка, равная 15%, для следующих трех лет она составляет 20%. Средняя ставка за весь срок ссуды равна

/-Vl,15²x1,2³ -1-0,17974 или 17,974%.

Рассмотрим теперь усреднение ставок, применяемых в не­скольких однородных операциях, которые различаются сумма­ми ссуд и процентными ставками. Искомые средние ставки на­ходим из условия равенства соответствующих сумм после нара­щения процентов. Так, если применяются простые ставки и сроки этих операций одинаковы (я), то из равенства

следует

5>,(1 +л/) = 2/>,(1 + */,)

Т-(4.4)

Как видим, весами здесь являются суммы ссуд.

Перейдем к усреднению сложных ставок для однородных ссудных операций. Пусть сроки операций одинаковы (п). Из равенства соответствующих множителей наращения следует

67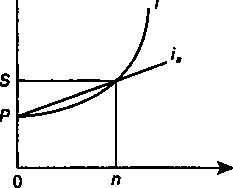

Формулы (4.4) и (4.5) получены для частных случаев, когда сроки ссуд одинаковы. В общих случаях они, разумеется, не ра­ботают. Однако решение соответствующих задач возможно, но более сложным путем.

§4.2. Эквивалентность процентных ставок

Как было показано ранее, для процедур наращения и дис­контирования могут применяться различные виды процентных ставок. Определим теперь те их значения, которые в конкрет­ных условиях приводят к одинаковым финансовым результа­там. Иначе говоря, замена одного вида ставки на другой при соблюдении принципа эквивалентности не изменяет финансо­вых отношений сторон в рамках одной операции. Для участ­вующих в сделке сторон в общем безразлично, какой вид став­ки фигурирует в контракте. Такие ставки назовем эквивалент-ними.

Проблема эквивалентности ставок уже затрагивалась в гл. 3 при определении эффективной ставки процента: сложная годо­вая ставка / эквивалентна ставке j при начислении процентов т раз в году. Рассмотрим теперь проблему эквивалентности ставок более полно и систематизированно. В принципе соот­ношение эквивалентности можно найти для любой пары раз­личного вида ставок — простых и сложных, дискретных и не­прерывных.

Формулы эквивалентности ставок во всех случаях получим исходя из равенства взятых попарно множителей наращения. Приведем простой пример. Определим соотношение эквива­лентности между простой и сложной ставками. Для этого при­равняем друг к другу соответствующие множители наращения:

(1 + ni_s) = (1 + /)",

где /₅ и / — ставки простых и сложных процентов.

Приведенное равенство предполагает, что начальные и нара­щенные суммы при применении двух видов ставок идентичны (см. рис. 4.1).

68

Сумма А

Срок




Рис. 4.1

Решение приведенного выше равенства дает следующие со­отношения эквивалентности:

_ (1 + 0^я

1,

(4.6)


/ - \1 + л/ - 1-

(4.7)

Аналогичным образом определим и другие, приведенные ни­же, соотношения эквивалентности ставок.

Эквивалентность простых процентных ставок. При выводе ис­комых соотношений между ставкой процента и учетной ставкой следует иметь в виду, что при применении этих ставок исполь­зуется временная база К= 360 или К= 365 дней. Если времен­ные базы одинаковы, то из равенства соответствующих множи­телей наращения следует:

'* \-nd:

(4.8)


^d' 1+w/

(4.9)

где п — срок в годах, /_s — ставка простых процентов, d_s— про­стая учетная ставка.

ПРИМЕР 4.3. Вексель учтен за год до даты его погашения по учетной ставке 15%. Какова доходность учетной операции в виде процентной ставки? По (4.8) находим

0,15

'^s 1-0,15

= 0,17647, или 17,647%.

69

Иначе говоря, операция учета по учетной ставке 15% за год дает тот же доход, что и наращение по ставке 17,647%.

Следует обратить внимание на то, что отношения эквива­лентности между простыми ставками i_sи d_sсущественно зави­сят от срока операции. Например, для d = 10 % находим следу­ющие размеры эквивалентных ставок:

п (в годах) 0,1 0,5 1 2 5 10

/,(%) 10,1 10,5 11,1 12,5 20 оо

Пусть срок ссуды измеряется в днях, тогда, подставив в (4.8) и (4.9) п = t/K (напомним, что / — срок наращения процентов в днях, К — временная база), получим варианты соотношений эквивалентности:

а) временные базы одинаковы и равны 360 дням:

360

'--1бо^' ^(4|0>

360/

". = 15П^ <⁴">

б) если при начислении процентов принята база К = 365, а
для учетной ставки К = 360, то

/- ³⁶⁵4 (4.2)

° 360 -td/^^Л1)

360/

ПРИМЕР 4.4. Необходимо найти величину учетной ставки, экви­валентной годовой процентной ставке 40% (К = 365) при условии, что срок учета равен 255 дням. Находим по формуле (4.13)

360 х 0,4 _{ЛОЛЛО|Г ЛЛЛ}о«,п,

^d= 365 + 255 х 0,4 ⁼ °'³⁰⁸³⁵' ^{ИШ 3}°'^835%-

70

Эквивалентность простых и сложных ставок. Рассмотрим со­отношения эквивалентности простых ставок i_sи d_s, с одной стороны, и сложных ставок / и у, с другой. Сложную учетную ставку здесь не будем принимать во внимание. Попарно при­равняв друг к другу соответствующие множители наращения, получим набор искомых соотношений.

Эквивалентность i_sи /. Формулы были получены выше (см. (4.6) и (4.7)).

(4.14) (4.15)

(4.16) (4.17)

(4.18) (4.19)

Эквивалентность i uj:

4--а	+ j/m)mn- 1 п
j -m	H/l+ >»",-1).
Эквивалентность dsи /:
4-	1 - (1 + 0я п
/ -	"J\-nds-l.
Эквивалентность dsи j:
„,=±	-(1 +j/m)mn п

j.mrⁿ^\-nd_s-l).

ПРИМЕР 4.5. Какой сложной годовой ставкой можно заменить в контракте простую ставку 18% (К= 365), не изменяя финансовых последствий? Срок операции 580 дней.

По формуле (4.7) находим эквивалентную сложную ставку:

/•.580/збф ₊ |§2₀1₈_1_₀₁₇1_{53/ или} 17,153%.

I ODD

Эквивалентность сложных ставок. Остановимся только на со­отношениях эквивалентности для ставок /, j и d. Имеем

/=(1 +j/ т)^т- 1, (4.20)

71

y-mCVuT-l). (4.21)

Эквивалентность i и d:

«"TT7- ^<4И>

Приведем еще несколько полезных соотношений, которые нетрудно получить на основе приведенных выше формул с уче­том того, что v = (1 + О""¹:

d = /v, (4.24)

v = 1 - d,(4.25)

1 - d = Id.(4.26)

Заметим, что в зависимостях (4.22)—(4.26) срок не играет никакой роли.

ПРИМЕР 4.6. При разработке условий контракта стороны дого­ворились о том, что доходность кредита должна составлять 24% годовых. Каков должен быть размер номинальной ставки при на­числении процентов ежемесячно, поквартально?

У

12(¹²Vl24 - 1) - 0,21705; j - 4(Vl24 - 1) - 0,22100.

Эквивалентность сложных дискретных и непрерывных ставок.

Теоретически можно найти соотношение эквивалентности ме­жду силой роста и любой дискретной процентной ставкой. Од­нако в этом, вероятно, нет необходимости. Ограничимся не­сколькими такими соотношениями, необходимость в которых может возникнуть в практических расчетах.

Эквивалентность 6 и i: см. формулы (3.27) и (3.28).

Эквивалентность д uj: из равенства 1 + — = е^ьследует

\ ^т)

j= _т(еЫт- 1), (4.27)

6 =/их 1п(1 + j/m).(4.28)

72

Эквивалентность б и d: из равенства (1 — d) ' = е^ьследует
6 = -lrt(l -
d = 1 - е^ь.(4.30)

ПРИМЕР 4.7. Какая непрерывная ставка заменит поквартальное начисление процентов по номинальной ставке 20%? Находим

6 = 4 х 1п(1 + 0,2) = 0,19516, или 19,516%

Формулы эквивалентности дискретных и непрерывных ста­вок позволяют расширить применение непрерывных процен­тов. Как уже говорилось выше, непрерывные проценты во мно­гих сложных расчетах позволяют существенно упростить вы­кладки. Вместе с тем такие ставки непривычны для практика, поэтому используя формулы эквивалентности, нетрудно пред­ставить полученные результаты в виде общепринятых характе­ристик.

§4.3. Финансовая эквивалентность обязательств и конверсия платежей

Финансовая эквивалентность обязательств. На практике не­редко возникают случаи, когда необходимо заменить одно де­нежное обязательство другим, например с более отдаленным сроком платежа, объединить несколько платежей в один (кон­солидировать платежи) и т.п. Ясно, что такие изменения не мо­гут быть произвольными. Неизбежно возникает вопрос о прин­ципе, на котором должны базироваться изменения условий контрактов. Таким общепринятым принципом является финан­совая эквивалентность обязательств. Эквивалентными считают­ся такие платежи, которые, будучи "приведенными" к одному моменту времени {focal date), оказываются равными. Приведе­ние осуществляется путем дисконтирования (приведение к бо­лее ранней дате) или, наоборот, наращения суммы платежа (ес­ли эта дата относится к будущему). Если при изменении усло­вий контракта принцип финансовой эквивалентности не со­блюдается, то одна из участвующих сторон терпит ущерб, раз­мер которого можно заранее определить.

73

Применение принципа финансовой эквивалентности не ог­раничено рамками задач изменения контрактов. Он лежит в ос­нове преобладающего числа методов количественного финан­сового анализа.

По существу, принцип эквивалентности в наиболее простом проявлении следует из формул наращения и дисконтирования, связывающих величины Р и S. Сумма Р эквивалентна S при принятой процентной ставке и методе ее начисления. Две сум­мы денег S_{и S₂, выплачиваемые в разные моменты времени, считаются эквивалентными, если их современные (или нара­щенные) величины, рассчитанные по одной и той же процент­ной ставке и на один момент времени, одинаковы. Замена S_{ на S₂в этих условиях формально не изменяет отношения сто­рон.

ПРИМЕР 4.8. На принципе эквивалентности основывается срав­нение разновременных платежей. Покажем это на примере. Имеются два обязательства. Условия первого: выплатить 400 тыс. руб. через 4 месяца; условия второго: выплатить 450 тыс. руб. через 8 месяцев. Можно ли считать их равноценными? Так как платежи краткосрочные, то при дисконтировании на начало срока применим простую ставку, равную, допустим, 20 %. Полу­чим

400
Р_А= = 375,00;

1+^0.2

450
Р₂ = = 397,06 тыс. руб.

^1+40-2

Как видим, сравниваемые обязательства не являются эквива­лентными при заданной ставке и в силу этого не могут адекватно заменять друг друга.

Сравнение платежей предполагает использование некоторой процентной ставки и, следовательно, его результат зависит от выбора ее размера. Однако, что практически весьма важно, та­кая зависимость не столь жестка, как это может показаться на первый взгляд. Допустим, сравниваются два платежа S_xи »У₂ со сроками л, и л₂, причем S_x < S₂и л, < л₂. Соотношение их со­временных стоимостей зависит от размера процентной ставки (см. рис. 4.2).

74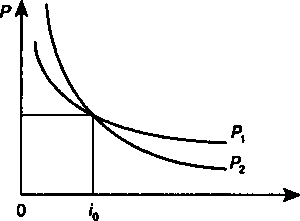







Рис. 4.2

С ростом i размеры современных стоимостей уменьшаются, причем при / = /₀ наблюдается равенство Р_х= Р_тДля любой ставки / < /₀ имеем Р_{ < Р₂. Таким образом, результат сравне­ния зависит от размера ставки, равного /₀. Назовем эту ставку критической или барьерной. Подробнее о барьерных экономиче­ских параметрах будет сказано в гл. 7. Здесь же офаничимся расчетом барьерной ставки. На основе равенства

11

1 + /i,/₀

1 + /i₂/₀

находим

i-4

'о S,

_V² _{" "'}

(4.31)



ПРИМЕР 4.9. Для данных примера 4.8 получим

400


1 -
450

'° 400 _8_ 450 ^Х 12

_4_ 12

= 0,428, или 42,8 %.

Таким образом, соотношение Р₂ > Р, справедливо при любом уровне процентной ставки, который меньше 42,8 %.

Если дисконтирование производится по сложной ставке, то критическую ставку найдем из равенства

75

$(1 + 4,)""'-s₂(u/bP.

В итоге

/о=^я-^яе-1. (4.32)

Консолидирование (объединение) задолженности. Как уже бы­ло сказано выше, принцип финансовой эквивалентности плате­жей применяется при различных изменениях условий выплат денежных сумм: их объединении, изменении сроков (досроч­ном погашении задолженности или, наоборот, пролонгирова­нии срока) и т.п. Общий метод решения подобного рода задач заключается в разработке так называемого уравнения эквива­лентности (equation of value), в котором сумма заменяемых пла­тежей, приведенных к какому-либо моменту времени, прирав­нивается к сумме платежей по новому обязательству, приведен­ных к той же дате. Для краткосрочных обязательств приведение осуществляется обычно на основе простых ставок, для средне-и долгосрочных — с помощью сложных процентных ставок. За­метим, что в простых случаях часто можно обойтись без разра­ботки и решения уравнения эквивалентности.

Одним из распространенных случаев изменения условий контрактов является консолидация (объединение) платежей. Пусть платежи S_v£₂,..., S_mсо сроками л,, я₂,—, п_тзаменяются одним в сумме S₀и сроком л₀. В этом случае возможны две по­становки задачи: если задается срок л₀, то находится сумма S₀ и наоборот, если задана сумма консолидированного платежа S₀, то определяется срок л₀. Рассмотрим обе постановки задачи.

Определение размера консолидированного платежа. При реше­нии этой задачи уравнение эквивалентности имеет простой вид. В общем случае, когда л,<л₂<...<л_т, искомую величину находим как сумму наращенных и дисконтированных платежей. Так, при применении простых процентных ставок получим

S₀= XSj(\ + tjl) + 2^(1 + t_ki)\(4.33)

j *•

где Sj — размеры объединяемых платежей со сроками л_у. < л₀, S_k— размеры платежей со сроками п_к > л₀,

/_у= До-Лу, t_k = п_к- п₀.

76

ПРИМЕР 4.10. Два платежа 1 и 0,5 млн руб. со сроками уплаты соответственно 150 и 180 дней объединяются в один со сроком 200 дней. Пусть стороны согласились на применении при конвер­сии простой ставки, равной 20%. Консолидированная сумма дол­га составит

20^=m_{02) + 500(1+}mz_l80
365 365
S₀ = 1000(1 + _ogc 0,2) + 500(1 + _ogc 0,2) =

= 1532,87 тыс. руб.

Консолидацию платежей можно осуществить и на основе сложных процентных ставок. Вместо (4.33) для общего случая (л, < п₀ < п_т) получим

So-2^sj(^l*ⁱf*2M^l+l)^k- ⁽⁴-³⁴⁾

ПРИМЕР 4.11. Платежи в 1 и 2 млн руб. и сроками уплаты через 2 и 3 года объединяются в один со сроком 2,5 года. При консоли­дации используется сложная ставка 20%. Искомая сумма составит

S₀ = 1000 х 1,2⁰-⁵ + 2000 х 1,2-°-⁵ = 2921,187 тыс. руб.

Определение срока консолидированного платежа. Если при объ­единении платежей задана величина консолидированного плате­жа S₀, то возникает проблема определения его срока л₀. В этом случае уравнение эквивалентности удобно представить в виде ра­венства современных стоимостей соответствующих платежей.

При применении простой ставки это равенство имеет вид

SoO+vr¹ =25_у(1+_Лу#г^!,

откуда

*

я₀ = - h= - 1 . (4.35)

Очевидно, что решение может быть получено при условии, что S₀> 2^.(1 + /ly/)"¹, иначе говоря, размер заменяющего пла­тежа не может быть меньше суммы современных стоимостей заменяемых платежей. Заметим также, что искомый срок про­порционален величине консолидированного платежа.

77

ПРИМЕР 4.12. Суммы в размере 10, 20 и 15 млн руб. должны быть выплачены через 50, 80 и 150 дней соответственно. Сторо­ны согласились заменить их одним платежом.

Современная стоимость заменяемых платежей (обозначим эту величину через Р) при условии, что / = 10% и К= 365, составит

Р= Ю(1 + Л- 0,1)"¹ + 20(1 + -Ц- 0,1)"¹ + 15(1 + || 0,1)-' =

43,844 млн руб. Согласно (4.35) находим

п₀= qV 43^44 " Ч ^{= 1,4}°^{4 Г0Да}' ^{ИЛИ 512 ДНвЙ}*

Продолжим пример. Пусть теперь размер заменяющего плате­жа задан в сумме 45 млн руб. Тогда срок заметно сократится и станет равным 0,264 года, или 96 дням.

Перейдем к определению срока консолидированного плате­жа на основе сложных процентных ставок. Уравнение эквива­лентности запишем следующим образом

*(|+'П-2 */(!♦')'■'•

У Для упрощения дальнейшей записи примем

с-2*_У(1+'Р.

После чего находим

_К8

^{"°=ыГ?п-<4-36>}

Как видим, решение существует, если S₀ > Q. Для частного случая, когда S₀= ZtS_J9при определении срока консолидирую­щего платежа иногда вместо (4.36) применяют средний взве­шенный срок:

"о—^ ⁽⁴-³⁷⁾

78

Привлекательность этой формулы, помимо ее простоты, со­стоит в том, что она не требует задания уровня процентной ставки. Однако надо помнить, что она дает приближенный ре­зультат, который больше точного. Чем выше ставка /, тем боль­ше погрешность решения по формуле (4.37).

ПРИМЕР 4.13. Воспользуемся данными примера 4.11 и опреде­лим срок консолидированного платежа в сумме 3 млн руб. Точное значение срока находим по (4.36). Для этого сначала рассчитаем

0= 1 х 1,2-2 +2 х 1,2"³= 1,8518.

После чего находим

N3/1,8518) _лалл ^По⁼ .Ш,2 =¹'^646г°А^а-

Приближенное решение дает 2,667 года.

§4.4. Общая постановка задачи изменения условий контракта

Обсудим теперь общие случаи изменения условий выплат, предусматриваемых в контрактах, для которых решение нельзя получить простым суммированием приведенных на некоторую дату платежей. Разумеется, и в таких случаях решение основы­вается на принципе эквивалентности платежей до и после из­менения условий. Метод решения заключается в разработке со­ответствующего уравнения эквивалентности. Если приведение платежей осуществляется на некоторую начальную дату, то по­лучим следующие уравнения эквивалентности в общем виде:

2&(1 + rijt) = 2^(1 + п_к1) — при использовании простых процентов,

Е ^J^vJ" Е ^^куПк" ^ПР^И использовании сложных процен-

j тов.

Здесь S. и л. — параметры заменяемых платежей, S_kи п_к— па­раметры заменяющих платежей.

Конкретный вид равенства определяется содержанием конт­рактов, поэтому методику разработки уравнений эквивалентно-

79

сти удобнее показать на примерах. Для этого рассмотрим три примера. В двух первых для дисконтирования применяются простые ставки, в последнем — сложные.

ПРИМЕР 4.14. Две суммы 10 и 5 млн руб. должны быть вы­плачены 1 ноября и 1 января следующего года. Стороны согласи­лись пересмотреть порядок выплат: должник 1 декабря выплачи­вает 6 млн руб. Остаток долга гасится 1 марта. Необходимо най­ти сумму остатка при условии, что пересчет осуществляется по ставке простых процентов, равной 20% (К= 365). Графическое изображение условий задачи приведено на рис. 4.3.

10 6 5 S = ?

Т ▼ V

1 н 1 д 1 я 1м

Рис. 4.3

Возьмем за базовую дату, допустим, момент выплаты 5 млн руб. Уравнение эквивалентности в этом случае выглядит следую­щим образом:

¹⁰⁽¹⁺-ik°'^{2)+ 5=6(1+} ^°-^{2)+S(1 +} -й-⁰-²)"¹-

Находим S = 9,531 млн руб.

Заметим, что изменение базовых дат приводит к некоторым, впрочем незначительным, смещениям результатов. Например, при приведении платежей к 1 марта получим следующее уравне­ние эквивалентности:

120 59 90

^{10(1 + ^°'2) + 5(1 + ^-°'2> = 6(1 + ^°»2> + S'}

Теперь S = 9,523 млн руб.

ПРИМЕР 4.15. Имеется обязательство уплатить 10 млн руб. через 4 месяца и 7 млн руб. через 8 месяцев после некоторой да­ты. По новому обязательству необходимо выплату произвести равными суммами через 3 и 9 месяцев. Изменение условий осу­ществляется с использованием простой ставки, равной 10% {К= 360). Примем в качестве базовой даты начало отсчета вре­мени. Уравнение эквивалентности в этом случае записывается следующим образом:

80

10(1 + 4/12 х 0,1)⁴ + 7(1 + 8/12 х 0.1)"¹ = = S(1 + 3/12 x O.D"¹ + S(1 + 9/12 x 0,1 Г¹. Следовательно, S = 8,521 млн руб.

Перейдем к примеру с применением сложной процентной ставки.

ПРИМЕР 4.16. Существует обязательство уплатить 100 тыс. руб. через 5 лет. Стороны согласились изменить условия погашения долга следующим образом: через два года выплачивается 30 тыс., а оставшийся долг — спустя 4 года после первой выпла­ты (см. рис .4.4). Необходимо определить сумму последнего пла­тежа.

30 100 S = ?

Y УV

0 2 5 6

Рис. 4.4

Уравнение эквивалентности составим на начало отсчета вре­мени:

100v⁵ = 30v² + Sv^e,

где v — дисконтный множитель.

Аналогичное по смыслу равенство можно составить на любую дату, например на конец шестого года. В этом случае

100(1 + I) = 30(1 + /)⁴ + S.

Данное уравнение легко получить из предыдущего, умножив его на (1 + /)⁶.

При решении любого из приведенных уравнений относительно S находим (при условии, что ставка равна 10% годовых) S = 133,233 тыс.руб. Выбор базовой даты при применении слож­ных процентов не влияет на результаты расчетов по замене пла­тежей.

81

§4.5. Налоги и инфляция

В рассмотренных выше методах определения наращенной суммы не учитывались такие важные моменты, как налоги и инфляция. Затронем эту проблему.

Налог на полученные проценты. В ряде стран полученные (юридическими, а иногда и физическими лицами) проценты облагаются налогом, что, естественно, уменьшает реальную на­ращенную сумму и доходность депозитной операции.

Обозначим, как и выше, наращенную сумму до выплаты на­логов, через 5, а с учетом их выплат как S". Пусть ставка нало­га на проценты равна g, а общая сумма налога G.

При начислении налога на проценты возможны два вариан­та: налог начисляется за весь срок сразу, т.е. на всю сумму про­центов, или последовательно по периодам, например в конце каждого года.

При начислении простых процентов за весь срок находим¹:

G = Pnig,
S" = S-(S- P)g= />[(1 + ai(1 - g)i].(4.38)

Таким образом, учет налога при определении наращенной суммы сводится к соответствующему сокращению процентной ставки — вместо ставки / фактически применяется ставка (1 — g)i. Размер налога пропорционален сроку.

Перейдем к долгосрочным операциям со сложными процен­тами. Начнем с варианта определения налога за весь срок. Его сумма равна

G = (S- P)g = />[(1 + 0- - l]g.(4.39)

Наращенная сумма после выплаты налога составит

5" = S - G = />[(1 - g)(l + tf + g].(4.40)

По второму варианту сумма налога определяется за каждый истекший год. Эта величина переменная — с ростом наращен­ной суммы растет и сумма налога. Рассчитаем налог на процен­ты за /-й год:

¹ Доказательство (4.38) см. в Математическом приложении к главе. 82

G, = (5, - S_Hl)g = />[(! + /У - (1 + /Г¹!* = ^(1 + О'"¹ ' x g-

За весь срок сумма налогов равна полученной выше величи­не¹:

Zc, = 5>(1 + 0^м' х_?= />[(1 + 0» - lfc = С. (4.41)

Иначе говоря, метод взыскания налога не влияет на общую его сумму. Однако, для плательщика налога далеко небезраз­лично, когда он его выплачивает.

ПРИМЕР 4.17. Пусть ставка налога на проценты равна 10%. Про­центная ставка — 30% годовых, срок начисления процентов — 3 года. Первоначальная сумма ссуды 1 млн руб. Определим разме­ры налога на проценты при начислении простых и сложных про­центов.

При начислении простых процентов за весь срок получим сле­дующие размеры наращенной суммы:

1900 тыс. руб. без уплаты налога,

S" = 1000[1 + 3(1 - 0,1)0,3] = 1810 тыс. руб. с учетом выпла­ты налога.

Начислим теперь сложные проценты:

2197 тыс. руб. без уплаты налога,

S" = 1000[(1 - 0,1)(1 + 0,3)³ + 0,1] = 2077,3 тыс. руб. с уче­том его выплаты за весь срок сразу. Сумма налога равна 119,7 тыс. руб.

При последовательной выплате налога:

за первый год выплачивается 1000 х 0,1 х0,3 = 30 тыс. руб., налог за второй год 1000 х 1,3 х 0,3 х 0,1 = 39. Наконец, за тре­тий год 1000 х 1,3² х 0,3 х 0,1 = 50,7. Общая сумма налога рав­на 119,7 тыс. руб.

Инфляция. В рассмотренных выше методах наращения все денежные величины измерялись по номиналу. Иначе говоря, не принималось во внимание снижение реальной покупательной способности денег за период, охватываемый операцией. Одна­ко в современных условиях инфляция в денежных отношениях играет заметную роль, и без ее учета конечные результаты час­то представляют собой условную величину.

Инфляцию необходимо учитывать по крайней мере в двух случаях: при расчете наращенной суммы денег и при измерении

¹ См. Математическое приложение к главе.

83

реальной эффективности (доходности) финансовой операции. Остановимся на этих проблемах. Введем обозначения:

S — наращенная сумма денег, измеренная по номиналу, С — наращенная сумма с учетом ее обесценения, У — индекс цен,

J_c— индекс, характеризующий изменение покупательной способности денег за период.

Очевидно, что

С=5хУ_с.

Индекс покупательной способности денег, как известно, ра­вен обратной величине индекса цен — чем выше цены, тем ни­же покупательная способность:

'■-i-

Указанные индексы, естественно, должны относиться к оди­наковым интервалам времени. Пусть, например, сегодня полу­чено 150 тыс. руб. Известно, что за два предшествующих года цены увеличились в 1,5 раза (или повышение на 50%), J_p= 1,5, индекс покупательной способности денег равен 1/1,5. Следова­тельно, реальная покупательная способность 150 тыс. руб. со­ставит 150/1,5 = 100 тыс. руб. в деньгах с покупательной спо­собностью двухлетней давности.

Нетрудно связать индекс цен и темп инфляции. Под темпом инфляции И понимается относительный прирост цен за период; обычно он измеряется в процентах и определяется как

А = 100Ц, - 1). В свою очередь

Например, если темп инфляции за период равен 30%, то это означает, что цены выросли в 1,3 раза.

Инфляция является цепным процессом. Следовательно, ин­декс цен за несколько периодов равен произведению цепных ин­дексов цен:

84

'>-ч[^,+-ш\<⁴-⁴²>

где А, — темп инфляции в периоде U

Пусть теперь речь пойдет о будущем. Если Л — постоянный ожидаемый (или прогнозируемый) темп инфляции за один пе­риод, то за п таких периодов получим

Грубейшей ошибкой, которая, к сожалению, встречается в российской практике, является суммирование (!) темпов ин­фляции отдельных периодов дня получения обобщающего по­казателя инфляции за весь срок. Что, заметим, существенно за­нижает величину получаемого показателя.

ПРИМЕР 4.18. Постоянный темп инфляции на уровне 5% в ме­сяц приводит к росту цен за год в размере

J_p= 1,05¹²= 1,796.

Таким образом, действительный годовой темп инфляции ра­вен 79,6%, а не 60% как при суммировании.

Продолжим пример. Пусть приросты цен по месяцам состави­ли: 1,5; 1,2 и 0,5%. Индекс цен за три месяца согласно (4.42) ра­вен

J_p= 1,015 х 1,012 х 1,005 = 1,0323. Темп инфляции за три месяца 3,23%.

Вернемся к проблеме обесценения денег при их наращении. Если наращение производится по простой ставке, то наращен­ная сумма с учетом покупательной способности равна

^ S „ 1 + л/ 1 + ni

р

^с"Т.-^р—Г"1—7V- ^<4-⁴⁴⁾

1 +

100

85

Как видим, увеличение наращенной суммы с учетом ее ин­фляционного обесценения имеет место только тогда, когда

1 +«/ > /„.

ПРИМЕР 4.19. На сумму 1,5 млн руб. в течение трех месяцев на­числяются простые проценты по ставке 28% годовых, наращенная сумма, следовательно, равна 1,605 млн руб. Ежемесячная инфля­ция характеризуется темпами 2,5; 2,0 и 1,8%. Индекс цен равен 1,025 х 1,02 х 1,018 = 1,06432. С учетом обесценивания наращен­ная сумма составит

1,605

- = 1,508 млн руб.

1,06432

Обратимся теперь к наращению по сложным процентам. На­ращенная сумма с учетом инфляционного обесценивания нахо­дится как

+ /

S (l ⁺ С« — -Р± <-_шр\

(4.45)

100

р

Величины, на которые умножаются Р в формулах (4.44) и (4.45), представляют собой множители наращения, учитываю­щие ожидаемый уровень инфляции. Посмотрим теперь, как со­вместно влияют сложная ставка / и темп инфляции Л на значе­ние этого множителя. Очевидно, что если среднегодовой темп инфляции равен процентной ставке, то роста реальной суммы не произойдет — наращение будет поглощаться инфляцией, и следовательно, С = Р. Если же Л/100 > /, то наблюдается "эро­зия" капитала —. его реальная сумма будет меньше первона­чальной. Только в ситуации, когда h/ЮО < /, происходит реаль­ный рост, реальное накопление (см. рис. 4.5). Очевидно, что при начислении простых процентов ставка, компенсирующая влияние инфляции, соответствует величине

п

Ставку, превышающую критическое значение /' (при начис­лении сложных процентов /' = Л), называют положительной ставкой процента.

86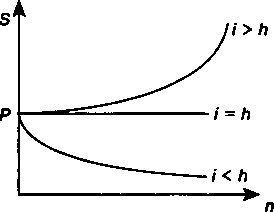

Рис. 4.5

Владельцы денег, разумеется, не могут смириться с их ин­фляционным обесценением и предпринимают различные по­пытки компенсации потерь. Наиболее распространенной явля­ется корректировка ставки процента, по которой производится наращение, т.е. увеличение ставки на величину так называемой инфляционной премии. Итоговую величину можно назвать брут-то-ставкой. (В западной финансовой литературе такую ставку иногда называют номинальной. Однако этот термин уже "за­нят" (см. номинальная и эффективная ставки в § 3.3.).

Определим брутто-ставку (обозначим ее как г) при условии полной компенсации инфляции. При наращении по сложной процентной ставке находим брутто-ставку из равенства

^,+'-^(|+/>(¹⁺Т5г)-

Откуда

г= / +

h 100

+ г

100

(4.46)

На практике скорректированную по темпу инфляции ставку часто рассчитывают проще, а именно:

г= / +

100'

(4.47)

Формула (4.46) по сравнению с (4.47) содержит один допол­нительный член, которым при незначительных величинах / и Л можно пренебречь. Если же они значительны, то ошибка (не в пользу владельца денег) станет весьма ощутимой. Например, даже при / = 5% и й = 1% "вклад" этого произведения в брут­то-ставку составит 0,005, или 0,5%. Брутто-ставка в этом случае

87

равна 15,5% (вместо 15% по формуле (4.47). Однако при годо­вой инфляции в 100% и той же исходной ставке наращения брутто-ставка увеличивается уже до 0,05 + 1 + 0,05 х 1 = 1,1, т.е. до 110%.

При наращении по простым процентам имеем

1 +лг=(1 + */)/,,

где У — индекс цен за учитываемый период.

Очевидно, что при больших темпах инфляции корректиров­ка ставки имеет смысл только для кратко- или в крайнем слу­чае среднесрочных операций.

Перейдем теперь к измерению реальной доходности финан­совой операции, т.е. доходности с учетом инфляции. Если г объявленная норма доходности (или брутто-ставка), то реаль­ный показатель доходности в виде годовой процентной ставки / можно определить при наращении сложных процентов на ос­нове (4.47):

1 + г

1+-*-100

Если брутто-ставка определяется по упрощенной формуле (4.47), то

Л

'"^г"1оо-

Аналогичный по содержанию показатель, но при начисле­нии простых процентов, находим как

1 /1 + пг \

^{■ «пМ- <4-49)}

Как видим, реальная доходность здесь зависит от срока опе­рации. Положительной простая ставка / может быть только при условии, что 1 + пг > J'

ПРИМЕР 4.20. Рассчитаем реальную годовую ставку для следу­ющих условий: годовой темп инфляции — 20%, брутто-ставка —

88

25% годовых, п= 0,5 года. Индекс цен за половину года: 1,2°'⁵= 1,0954.

Для простых процентов получим

1 /1 + 0,5 х 0,25 \

¹= ТТ Г^Гл Ч = 0,05404.

0,5 [ 1,0954 )

Изменим условия задачи. Пусть срок теперь равен 5 годам и речь идет о сложной ставке. Индекс цен за этот период 1,7. В этом случае

^«⁵VU-1«0_f11196,

1 + 0,25 '- 1+0.11106 -1-0.1241.

Компенсации инфляции можно достичь и путем индексации исходной суммы задолженности. В этом случае

С= PxJ_px(l + /)".

§4.6. Кривые доходности

Как уже говорилось выше, процентная ставка является изме­рителем доходности финансовой операции. Ее значение зави­сит от многих факторов. Для практика важно представить себе закономерность изменения величины доходности (или про­центных ставок, используемых в однородных по содержанию операциях), в зависимости от некоторых фундаментальных фа­кторов. Вероятно, наиболее важным из них является риск невоз­врата вложенных средств. Очевидно также, что подобного ро­да риск существенно зависит от срока ссуды. Так, при всех про­чих равных условиях ссуда на 5 лет более рискованна, чем, ска­жем, на 2 года. Компенсировать риск владельцу денег может повышение ожидаемой доходности, договорной процентной ставки. Таким образом, зависимость "доходность — риск" при­ближенно можно охарактеризовать с помощью зависимости "доходность — срок", получить которую для практических це­лей существенно проще. Такую зависимость, представленную в виде графика, называют кривой доходности (yield curve). На гра­фике по вертикали откладывают доходность (У), по горизонта­ли — срок (л) (см. рис. 4.6). Если график охватывает широкий

89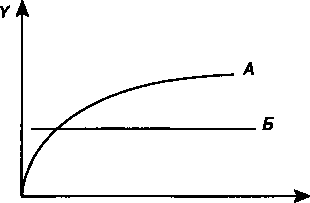



Рис. 4.6

диапазон сроков (как краткосрочные, так и долгосрочные опе­рации), что тоже практикуется, то для измерения срока приме­няют логарифмическую шкалу.

Кривые доходности обычно строятся раздельно для кратко-, средне- и долгосрочных операций и однородных кредитно-ссудных операций и финансовых инструментов. Наблюдаемые значения доходности обычно находятся около кривой или не­посредственно на ней. Конкретная кривая доходности отвечает реальной ситуации, сложившейся на денежно-кредитном рын­ке, и характерна для короткого временного периода. Изменение ситуации меняет форму кривой и ее положение на графике. В ряде западных периодических финансовых изданий регулярно приводятся такие кривые.

Для нормальных экономических условий кривая доходности имеет форму кривой А: доходность (Y) здесь растет по мере уве­личения срока. Причем каждая следующая единица прироста срока дает все меньшее увеличение доходности. Такую кривую называют положительной, или нормальной, кривой доходности (pozitive, normal yield curve). Нормальная форма кривой (не сле­дует путать с кривой нормального распределения, используемой в статистике) наблюдается в условиях, когда инвесторы в своей массе учитывают такие факторы, как рост неопределенности финансовых результатов (риска) при увеличении срока.

Кривая доходности, близкая к горизонтальной прямой (ли­ния Б), указывает на то, что инвесторы не принимают во вни­мание или в малой степени учитывают риск, связанный со сро­ком.

Иногда встречаются "отрицательные" и "сгорбленные" кри­вые (humped yield curve) доходности. Первая из названных кри­вых соответствует уменьшению доходности финансового инст­румента по мере роста срока (высокая нестабильность рынка,

90

ожидание повышения процентных ставок), вторая — падению доходности после некоторого ее роста.

Существуют несколько конкурирующих или, скорее, допол­няющих теорий, объясняющих закономерности "поведения" кривых доходности. Остановимся на двух из них: теории лик­видности (liquidity preference theory) и теории ожиданий (expecta­tions theory). Согласно первой изменения доходности связыва­ются с увеличением риска ликвидности инструмента в относи­тельно короткие сроки. Вторая из упомянутых теорий утвер­ждает, что форма кривой может рассматриваться как обобщен­ная характеристика ожиданий инвесторов, вернее, их поведе­ния в текущий момент в связи с ожиданиями изменений про­центных ставок в будущем. Однако интерпретация формы кри­вой в этом плане неоднозначна, да и не может быть иной, по­скольку приходится принимать во внимание по крайней мере действие двух факторов: риск и ожидание изменений ставок. Например, положительная кривая может интерпретироваться как указание на то, что инвесторы ожидают рост ставок в буду­щем. Иногда эта же форма кривой считается симптомом отно­сительной стабильности денежно-кредитного рынка.

Кривые доходности получили широкое распространение как инструмент анализа, помогающий при решении ряда инвести­ционных проблем, в частности, при сравнении доходности не­скольких финансовых инструментов, корректировке портфеля активов и т.д.¹

ПРИМЕР 4.21. Рассмотрим на условном примере один из про­стых способов применения кривой доходности применительно к расчету процентной ставки. Допустим, инвестор должен инвести­ровать некоторую сумму денег на 4 года. Причем в силу ряда при­чин у него есть только два варианта для этого: разместить эту сумму на депозитах сразу на весь срок или сначала на 3 года, а затем на 1 год. Пусть уровни ставок следуют нормальной кривой доходности: по трехлетним депозитам — 10%, по четырехлетним — 10,5% сложных годовых. Размер ставки для депозита на пос­ледний год в момент принятия решения, разумеется, неизвестен. Какой вариант размещения средств должен выбрать инвестор? Очевидно, что для того чтобы остановиться на втором варианте, он должен ожидать результат не хуже, чем при первом варианте. Задача, следовательно, сводится к определению того значения ставки для 4-го года, при котором оба варианта будут равноцен­ными в финансовом отношении.

¹ В гл. 7 приводится пример выбора поведения инвестора в зависимости от ожиданий размера процентной ставки.

91

Обозначим через /₃ и /₄ уровни процентных ставок для депози­тов на 3 и 4 года, а через /₀ — неизвестную ставку для годового депозита. В силу финансовой эквивалентности результатов поме­щения средств множители наращения для обоих вариантов долж­ны быть равными друг другу. Отсюда

(1+/₄)⁴ = (1 +'з>³0 + '<>>•
По данным примера находим ставку
(1+/₄)⁴ 1.Ю5⁴

>о = 7Гм7¹ "ТТ^"^{1 = 0,12}°^{14, или 12}«^014%-

I Таким образом, для того чтобы инвестор остановился на вто-j ром варианте, он должен ожидать, что через 3 года ставка по од­ногодичным депозитам будет не менее 12,014 %, т.е. уровень ставок повысится. Соответственно, если он ожидает, что ставка не достигнет этого уровня, следует выбрать первый вариант.

Математическое приложение к главе

1. Приведем доказательство формулы (4.38).
По определению

S" = S-(S- P)g, откуда

S* = (1 - g)S +flf- P(l - g)(l + ni) + Pg = P[l + n(l - g)i].

2. Докажем формулу (4.41):

G_t= (S_t- S^)g - P[(l + If - 0 + 0^M1* - Pd + ir¹ x/x«,

2c_r = p/g2(i + o^M.

Суммируются /i - 1 членов геометрической прогрессии:

Окончательно имеем

(?-/»[(! +О*-1]*.

ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА

1. 
   Четыркин Е.М. Методы финансовых и коммерческих расчетов. М.: Дело, 1995. Гл. 3.
   
2. 
   Четыркин Е.М., Васильева Н.Е. Финансово-экономические расчеты. М.: Фи­нансы и статистика, 1990. Гл. 2.
   
3. 
   Шарп Х.Ф., Александер ГДж., Бейли Дж.В. Инвестиции. М.: Инфра-М, 1997. Гл. 5, 13.
   
4. 
   Cartledge P. Financial arithmetic. A practitioners guide. Euromoney Books, 1993.