Е. М. Четыркин финансовая математика
 Скачать 4.63 Mb.
|
Часть из них получена за счет начисления процентов на проценты. Она составляет
О пOn Рис. 3.1 Рис. 3.2 Величину (1 + 0я называют множителем наращения (compoundinterestfactor) по сложным процентам. Значения этого множителя для целых чисел п приводятся в таблицах сложных процентов. Фрагмент такой таблицы приведен в табл. 2 Приложения. Точность расчета множителя в практических расчетах определяется допустимой степенью округления наращенной суммы (до последней копейки, рубля и т.д.). Время при наращении по сложной ставке обычно измеряется как ACT/ ACT. 44 ПРИМЕР 3.1. Какой величины достигнет долг, равный 1 млн руб., через 5 лет при росте по сложной ставке 15,5% годовых? По формуле (3.1) находим S= 1 000 000(1 + 0.155)5 = 2055464,22 руб. Как видим, величина множителя наращения зависит от двух параметров -/ил. Следует отметить, что при большом сроке наращения даже небольшое изменение ставки заметно влияет на величину множителя. В свою очередь очень большой срок приводит к устрашающим результатам даже при небольшой процентной ставке. Здесь уместна следующая иллюстрация. Остров Манхэттен, на котором расположена центральная часть Нью-Йорка, был куплен (а точнее выменен) за 24 долл.1 Стоимость земли этого острова 350 лет спустя оценивалась примерно в 40 млрд долл., т.е. первоначальная сумма увеличилась в 1,667 х 109 раз! Такой рост достигается при сложной ставке, равной всего 6,3 % годовых. Очевидно, что очень высокая (инфляционная) процентная ставка может быть применена только для короткого срока. В противном случае результат наращения окажется бессмысленным. Например, уже при / = 120% (а такая инфляционная ставка не столь уж давно наблюдалась в России, правда для краткосрочных ссуд) и п = 10 имеем чудовищный по размеру множитель наращения (1 + 1,2)10 = 2656. Формула наращения по сложным процентам (3.1) получена для годовой процентной ставки и срока, измеряемого в годах. Однако ее можно применять и при других периодах начисления. В этих случаях / означает ставку за один период начисления (месяц, квартал и т.д.), ая- число таких периодов. Например, если i — ставка за полугодие, то п — число полугодий и т.д. Формулы (3.1)—(3.3) предполагают, что проценты на проценты начисляются по той же ставке, что и при начислении на основную сумму долга. Усложним условия начислений процентов. Пусть проценты на основной долг начисляются по ставке /, а проценты на проценты — по ставке г * / В этом случае S= Р + А[1 + (1 + г) + (1 + г)2 +...+ (1 + г)"""1]. Ряд в квадратных скобках представляет собой геометрическую прогрессию с первым членом, равным 1, и знаменателем (1 + г). В итоге имеем (3.4) ( (I+ г)" - О S= Р 1 + /^ -1 - 1 См.: Томас Д. Воротилы финансового мира. М.: Прогресс, 1976. 45 Начисление процентов в смежных календарных периодах. Выше при начислении процентов не принималось во внимание расположение срока начисления процентов относительно календарных периодов. Вместе с тем, часто даты начала и окончания ссуды находятся в двух периодах. Ясно, что начисленные за весь срок проценты не могут быть отнесены только к последнему периоду. В бухгалтерском учете, при налогообложении, наконец, в анализе финансовой деятельности предприятия возникает задача распределения начисленных процентов по периодам. Алгоритм деления общей массы процентов легко сформулировать на основе графика, построенного для двух смежных календарных периодов (см. рис. 3.2). Общий срок ссуды делится на два периода п{и птСоответственно, /=/, + /2, где /, = />[(1 + 0*| - 1)]; /2 = Р(\ + /ц[(1 + Оъ - 1] = = />[(1 + /)« - (1 + /)/!,]. ПРИМЕР 3.2. Ссуда была выдана на два года — с 1 мая 1998 г. по 1 мая 2000 г. Размер ссуды 10 млн руб. Необходимо распределить начисленные проценты (ставка 14% ACT/ACT) по календарным годам. Получим следующие суммы процентов (в тыс. руб.): 2± за период с 1 мая до конца года (244 дня): 10 000(1,14365 - 1) = = 915,4; Л± за 1999 г.: 10 000 х 1.14365 х 0,14 = 1528,2; 1 244 наконец, с 1 января до 1 мая 2000 г. (121 день): 10 000 х 1,14 365 х 121 х (1,14365 - 1) = 552,4. Итого за весь срок — 2996 тыс. руб. Такой же результат получим для всего срока в целом: 10 000х(1,142-1) = 2996. Переменные ставки. Формула (3.1) предполагает постоянную ставку на протяжении всего срока начисления процентов. Неустойчивость кредитно-денежного рынка заставляет модернизировать "классическую" схему, например, с помощью применения плавающих ставок (floatingrate). Естественно, что расчет 46 на перспективу по таким ставкам весьма условен. Иное дело — расчет постфактум. В этом случае, а также тогда, когда изменения размеров ставок фиксируются в контракте, общий множитель наращения определяется как произведение частных, т.е. 5-/>(1 + /1)Я'(и/2)Я2...(1+/,)Л4, (3.5) где /,, /2,..., ik— последовательные значения ставок; nvя2>—> пк— периоды, в течение которых "работают" соответствующие ставки. ПРИМЕР 3.3. Срок ссуды — 5 лет, договорная базовая процентная ставка — 12% годовых плюс маржа 0,5% в первые два года и 0,75% в оставшиеся годы. Множитель наращения в этом случае составит q= (1 + 0,125)2(1 + 0.1275)3 = 1,81407. Начисление процентов при дробном числе лет. Часто срок в годах для начисления процентов не является целым числом. В правилах ряда коммерческих банков для некоторых операций проценты начисляются только за целое число лет или других периодов начисления. Дробная часть периода отбрасывается. В большинстве же случаев учитывается полный срок. При 4этом применяют два метода. Согласно первому, назовем его общим, расчет ведется непосредственно по формуле (3.1). Второй, смешанный, метод предполагает начисление процентов за целое число лет по формуле сложных процентов и за дробную часть срока по формуле простых процентов: £=/>(1 +/)<(1 + */), (3.6) где л = а + Ъ — срок ссуды, а — целое число лет, b— дробная часть года. Аналогичный метод применяется и в случаях, когда периодом начисления является полугодие, квартал или месяц. При выборе метода расчета следует иметь в виду, что множитель наращения по смешанному методу оказывается несколько больше, чем по общему, так как для п < 1 справедливо соотношение 1 + л/ > (1 + /)Л. Наибольшая разница наблюдается при Ъ = 1/2. 47  ПРИМЕР 3.4. Кредит в размере 3 млн руб. выдан на 2 года и 160160 дней (п = 3 -г^ = 3,43836 года) под 16,5% сложных годовых. 365 Сумму долга на конец срока определим по формуле (3.1): S = 3 000 000 х 1.1653'43836 = 5071935,98 руб., в свою очередь, смешанный метод дает S = 3 000 000 х 1,1653 х (1 + 0,43836 х 0,165) = 5086595,98 руб. §3.2. Сравнение роста по сложным и простым процентам Для того чтобы сопоставить результаты наращения по разным процентным ставкам, достаточно сравнить соответствующие множители наращения. Нетрудно убедиться в том, что при одинаковых уровнях процентных ставок соотношения этих множителей существенно зависят от срока. В самом деле, при условии, что временная база для начисления процентов одна и та же, находим следующие соотношения (в приведенных ниже формулах подписной индекс sпроставлен у ставки простых процентов): — для срока меньше года простые проценты больше слож ных: (1 + nis) > (1 + /)«, — для срока больше года сложные проценты больше про стых: (1 + nis) < (1 + /)«, — для срока, равного году, множители наращения равны друг другу. Заметим также, что при п > 1 с увеличением срока различие в последствиях применения простых и сложных процентов усиливается. Графическую иллюстрацию соотношения множителей наращения см. на рис. 3.3. В табл. 3.1 приведены значения множителей наращения для /5 = / = 12%, К = 365 дней. 48 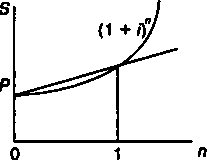 1 + ni9 Рис. 3.3 Таблица 3.1
Формулы удвоения. Наиболее наглядно влияние вида ставки можно охарактеризовать, сопоставляя числа лет, необходимые для удвоения первоначальной суммы. На основе (2.1) и (3.1) получим следующие формулы удвоения: — удвоение по простым процентам: 1 *,' п = удвоение по сложным процентам: п = 1п2 0,69315 1п(1 + /) 1п(1 + 0  ПРИМЕР 3.5. Найдем сроки удвоения для /s = / = 22,5%:1 .. In2 = 3,04. л = 1Ш.225 0,225 = 4,44; п= §3.3. Наращение процентов т раз в году. Номинальная и эффективная ставки Номинальная ставка. В современных условиях проценты капитализируются, как правило, не один, а несколько раз в году — по полугодиям, кварталам и т.д. Некоторые зарубежные коммерче- 49 ские банки практикуют даже ежедневное начисление процентов. При начислении процентов несколько раз в году можно воспользоваться формулой (3.1). Параметр п в этих условиях будет означать число периодов начисления, а под ставкой / следует понимать ставку за соответствующий период. Например, при поквартальном начислении процентов за 5 лет общее число периодов начисления составит 5 х 4 = 20. Множитель наращения по квартальной (сложной) ставке 8% равен в этом случае 1,0820 = 4,6609. На практике, как правило, в контрактах обычно фиксируется не ставка за период начисления, а годовая ставка, одновременно указывается период начисления процентов. Например, "18% годовых с поквартальным начислением" процентов. Итак, пусть годовая ставка равна у, число периодов начисления в году — /и. Каждый раз проценты начисляются по ставке j/m. Ставку у называют номинальной (nominalrate). Формулу наращения теперь можно представить следующим образом: S=p(l+AN,(3.7) где N — общее количество периодов начисления. Если N целое число (N= л/и), то в большинстве случаев для определения величины множителя наращения можно воспользоваться таблицей сложных процентов (табл. 2 Приложения). Например, при у = 20% и поквартальном начислении процентов (т = 4) в течение 5 лет отыскиваем табличное значение множителя для / = 20/4 = 5% и п = 5 х 4 = 20; находим q= 2,653298. ПРИМЕР 3.6. Изменим одно условие в примере 3.1. Пусть теперь проценты начисляются не раз в году, а поквартально. В этом случае N = 20 и S= 1 000 000| 1 + Напомним, что при ежегодном начислении процентов мы получили S= 2055464,22. Нетрудно догадаться, что чем чаще начисляются проценты, тем быстрее идет процесс наращения (цепной процесс). Для иллюстрации сказанного приведем значения множителей для J= 20% и п = 10 лет и разной частоте наращения в пределах года: 50
Как следует из приведенных данных, наибольшую "прибавку" в наращении дает переход от ежегодного начисления процентов к полугодовому, наименьший эффект — переход от ежемесячного к ежедневному. ПРИМЕР 3.7. Какова сумма долга через 25 месяцев, если его первоначальная величина 500 тыс.руб., проценты сложные, ставка 20% годовых, начисление поквартальное? По условиям задачи число периодов начисления Л/ = 25 : 3 = = 8 1/3. Применим два метода наращения — общий и смешанный (см. (3.6)). Получим 8! S « 500 OOof 1 + ^р] 3 - 75084ft04 руб., S = 500 000И + -^-)8 х И + у х -^-] = 751039,85 руб. Эффективная ставка. Введем теперь новое понятие — действительная, или эффективная ставка процента (effectiverate). Эта ставка измеряет тот реальный относительный доход, который получают в целом за год. Иначе говоря, эффективная ставка — это годовая ставка сложных процентов, которая дает тот же результат, что и m-разовое начисление процентов по ставке j/m. Обозначим эффективную ставку через /. По определению множители наращения по двум ставкам (эффективной и номинальной при m-разовом начислении) должны быть равны друг другу: Из равенства множителей наращения следует «-(l +£)"-!. (3-8) Эффективная ставка при т > 1 больше номинальной. Замена в договоре номинальной ставки jпри m-разовом начислении процентов на эффективную ставку / не изменяет финансовых обязательств участвующих сторон. Обе ставки эквива- 51  лентны в финансовом отношении. Отсюда, кстати, следует, что разные по величине номинальные ставки оказываются эквивалентными, если соответствующие им эффективные ставки имеют одну величину.ПРИМЕР 3.8. Каков размер эффективной ставки, если номинальная ставка равна 25% при помесячном начислении процентов? Имеем ,-^+^.j»., =0.280732. Для участвующих в сделке сторон безразлично применить ставку 25% при помесячном начислении процентов или годовую (эффективную) ставку 28,0732%. Для сокращения дальнейшей записи используем символ /т\ означающий размер номинальной ставки и количество начислений за год. Эквивалентная замена номинальной ставки имеет место только в том случае, когда удовлетворяется равенство 1 + А щ т, т2 1+4— Поскольку т может иметь только целые значения, то удобнее определять значение новой ставки, задаваясь величиной т? /О" г) ■>■> т2 mi1+4- щ -1  ПРИМЕР 3.9. Определим номинальную ставку /4>, которая безубыточно заменит ставку/12' = 25% в примере 3.8. Получим12 У<4» - 4 К£)4- 0,25524. 52 Таким образом, сокращение количества начислений потребует увеличения ставки с 25 до 25, 524 %. При подготовке контрактов может возникнуть необходимость в определении у по заданным значениям / и т. Находим у «/w(wVT77-l). (3.9) §3.4. Дисконтирование по сложной ставке При изучении простых процентов мы рассматривали математическое дисконтирование и банковский (коммерческий) учет. Первое заключалось в определении Р по значению S при заданной ставке процента, второе — при заданной учетной ставке. Применим первый метод и дисконтируем теперь сумму *Упо сложной ставке процентов. На основе (3.1) получим P = -^T^T=Sv",(3.10) v- = (1 + ,уп = -L (з.ц) Ч Величину v называют дисконтным, учетным, или дисконтирующим, множителем (compound discount factor). Значения этого множителя легко табулировать. В Приложении приведен фрагмент такой таблицы (см. табл. 3). Для случаев, когда проценты начисляются т раз в году, получим Р Svm\ Л™ (3.12) 1 + ^-т \*тп -И+-£| • (3.13) Напомним, что величину Р, полученную дисконтированием S, называют современной, текущей, стоимостью, или современной величиной S. Современная стоимость может быть рассчитана на любой момент до выплаты суммы S. 53  Разность S - Р, в случае, когда Р определено дисконтированием, называют дисконтом. Обозначим последний через D:Z) = 5- P= S(\ - V). ПРИМЕР 3.10. Сумма в 5 млн руб. выплачивается через 5 лет. Необходимо определить ее современную величину при условии, что применяется ставка сложных процентов, равная 12% годовых. Дисконтный множитель для данных условий составит у5= 1,12-5 = 0,56574, т.е. первоначальная сумма сократилась почти на 44%. Современная величина равна Р = 5000 х 1,12-5 = 2837,1 тыс. руб. Как уже отмечалось в гл. 2, современная величина платежа — одна из важнейших характеристик, применяемых в финансовом анализе. Кратко остановимся на некоторых ее формальных свойствах. Прежде всего отметим очевидное свойство — чем выше ставка процента, тем сильнее дисконтирование при всех прочих равных условиях (см. рис. 3.4). Например, если в примере 3.10 увеличить ставку вдвое, то дисконтный множитель снизится с 0,56574 до 0,34111. Значение дисконтного множителя уменьшается и с ростом величины т. 1 о ' Рис. 3.4 Влияние срока платежа также очевидно — с увеличением срока величина современной стоимости убывает. Отсюда следует, что при очень больших сроках она крайне незначительна. Например, если взять ставку / = 12% , то для п = 10, 50 и 100 находим следующие значения дисконтных множителей: 0,32197; 0,00346 и 0,000012. 54  Высокие, и особенно инфляционные, ставки, примененные для дисконтирования, приводят к бессмысленным результатам даже при сравнительно небольших сроках: например, для ставки 200% и сроке 5 лет дисконтный множитель равен 0,004116, т.е. близок к нулю.§3.5. Операции со сложной учетной ставкой Учет по сложной учетной ставке. В практике учетных операций иногда применяют сложную учетную ставку {compound dis-cound rate). В этих случаях процесс дисконтирования происходит с замедлением, так как каждый раз учетная ставка применяется не к первоначальной сумме (как при простой учетной ставке), а к сумме, дисконтированной на предыдущем шаге во времени. Дисконтирование по сложной учетной ставке осуществляется по формуле Р =5(1 - d)\(3.14) где d — сложная годовая учетная ставка. ПРИМЕР 3.11. Долговое обязательство на сумму 5 млн руб., срок оплаты которого наступает через 5 лет, продано с дисконтом по сложной учетной ставке 15% годовых. Каков размер полученной за долг суммы и величина дисконта (в тыс. руб.)? Имеем Р = 5000(1 - 0,15)5 = 2218,5; D = 5000 - 2218,5 = 2781,5. Если применить простую учетную ставку того же размера, то Р = 5000(1 - 5 х 0,15) = 1250; D = 5000 - 1250 = 3750. Как следует из приведенного примера, дисконтирование по сложной учетной ставке выгоднее для должника, чем по простой учетной ставке. Сказанное становится понятным при сравнении формул для дисконтных множителей: ws= (1 - nds) Hw=(l-rf)«, где ds, d — простая и сложная учетные ставки соответственно. Согласно первой из приведенных формул значение дисконтного множителя равномерно уменьшается по мере роста п и до- 55 стигает нуля при п = \/d. Согласно второй — множитель экспоненциально уменьшается и достигает нуля лишь в пределе, при п = оо. Величины дисконтных множителей при применении простой и сложной учетных ставок показаны на рис. 3.S 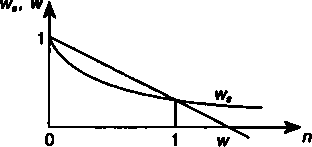 Рис. 3.5 Номинальная и эффективная учетные ставки. Дисконтирование может производиться не один, а т раз в году, т.е. каждый раз учет производится по ставке f/m . В этом случае />=£ 1 f\mn т (3.15) где/— номинальная годовая учетная ставка. Эффективная учетная ставка (d) характеризует степень дисконтирования за год. Определим ее на основе равенства дисконтных множителей: откуда f \mn (1-^ = |1-^| d = 1 т  В свою очередь/-m(l-*VT^f). Эффективная учетная ставка во всех случаях, когда т > 1, меньше номинальной. ПРИМЕР 3.12. По данным примера 3.11 определим сумму, полученную при поквартальном учете по номинальной учетной ставке 15%, и эффективную учетную ставку. Имеем f = 0,15; т= 4; тп= 20; 56  ,(,-*5f- P = 5000 1 - -^— = 2328,0 тыс. руб. Эффективная учетная ставка составит -^)'.w ( 0,15^4 d=1- 1--T— = 0.14177, или 14,177%. Наращение по сложной учетной ставке. Иногда наращенную сумму получают и с помощью сложной учетной ставки. Из формул (3.14) и (3.15) следует: *-7П^г <3|6> т Множитель наращения при использовании сложной ставки d равен (1 - d)n. §3.6. Сравнение интенсивности процессов наращения и дисконтирования по разным видам процентных ставок Выше для наращения и дисконтирования использовались ставки is, i,j, ds, d,f. Заметим, что даже в одинаковых исходных условиях применение этих ставок приводит к различным результатам. В связи с этим представляет практический интерес сравнение результатов наращения и дисконтирования по различным ставкам. Для этого достаточно сопоставить соответствующие множители наращения. Аналогичное можно проделать и с дисконтными множителями. Проблема сопоставления скорости роста при наращении по простой и сложной ставкам была затронута в § 3.2. Опустив формальные доказательства, запишем сразу необходимые соотношения при условии, что размеры ставок одинаковые. Варианты со ставками у и /рассматривать не будем, так как результат зависит и от значения /и. 57 Множители наращения соотносятся между собой следующим образом: (1+,Г<1+Я/,<-Г^Г<7]-Г^Г при 0 < Ж 1, 1 + /=1 + /;<т 1 - d при п = 1, 1+Ч<о + о-<7гг^г<—^ "ри«>1. Как видим, соотношения множителей зависят от сроков наращения процентов. Так, для срока, превышающего год, наибольший рост дает простая учетная ставка, наименьший — ставка простых процентов. В табл. 3.2 приведены значения множителей наращения для разных видов ставок при условии, что их размеры одинаковы — 20%. Таблица 3.2
Аналогичным образом получим соотношения для дисконтных множителей: (1-4я<1-ч<т^<7Г"Ьг' при0<я<ь ld=ld'<TTT3SlT7 прия = 1> >-Ч<(1-^<тгТо;г<-П^ ПРИЛ>1- 58 Для срока более года наиболее сильно дисконтирование проявляется при применении простой ставки процента и в наименьшей степени — при использовании простой учетной ставки. §3.7. Определение срока ссуды и размера процентной ставки При разработке условий финансовых операций часто сталкиваются с необходимостью решения обратных задач — расчетом продолжительности ссуды или уровня процентной ставки. Для простых процентов эти задачи рассмотрены в гл. 2. Обратимся к операциям со сложными ставками и решим уравнения, связывающие Р и S, относительно интересующих нас величин. Полученные формулы приводятся без доказательств, поскольку вывод их элементарен. Срок ссуды. Приведем формулы расчета п для различных условий наращения процентов и дисконтирования. При наращении по сложной годовой ставке / и по номинальной ставке у на основе формул (3.1) и (3.7) имеем ""togd+O* (ЗЛ8) \QS(S/P) п- '. -Г.(3.19) т х log 1 + — При дисконтировании по сложной годовой учетной ставке d и по номинальной учетной ставке/получим ШР/S) "=log(l-(320) ШР/S)„„, т х log я= ;—. (3.21) ПРИМЕР 3.13. За какой срок в годах сумма, равная 75 млн руб., достигнет 200 млн руб. при начислении процентов по сложной 59   ставке 15% раз в году и поквартально? По формулам (3.18) и (3.19) получим следующие сроки:log(200/75) 7л^о П= Юд1.1Б =7-0178ro«a- log(200/75) e еел, п= 2— ^ = 6,6607 года. 4 ж,og 1 + 0^i Величина процентной ставни. Приведем формулы для расчета ставок /, j, d, /для различных условий наращения процентов и дисконтирования. Они получены при решении уравнений, связывающих S и Р. При наращении по сложной годовой ставке процентов / и по номинальной ставке j получим / - n4s I P - 1, (3.22) j = m^nyjI7P-l).(3.23) При дисконтировании по сложным учетным ставкам d и / d « 1 - fjp 1S,(3.24) /«m(l-*V^7?). (3.25) ПРИМЕР 3.14. Сберегательный сертификат куплен за 100 тыс. руб., выкупная его сумма 160 тыс. руб., срок 2,5 года. Каков уровень доходности инвестиций в виде годовой ставки сложных процентов? По формуле (3.23) находим /.2^6 _1.0,20684. ПРИМЕР 3.15. Срок до погашения векселя равен 2 годам. Дисконт при его учете составил 30%. Какой сложной годовой учетной ставке соответствует этот дисконт? Применим формулу (3.24). По данным задачи P/S=0,7, откуда d-1-Voj «0,16334 60 §3.8. Непрерывное наращение и дисконтирование. Непрерывные проценты В практических финансово-кредитных операциях непрерывное наращение, т.е. наращение за бесконечно малые отрезки времени, применяется крайне редко. Существенно большее значение непрерывное наращение имеет в анализе сложных финансовых проблем, например при обосновании и выборе инвестиционных решений, в финансовом проектировании. С помощью непрерывных процентов удается учесть сложные закономерности процесса наращения, например использовать изменяющиеся по определенному закону процентные ставки. При непрерывном наращении процентов применяют особый вид процентной ставки — силу роста (force of interest). Сила роста характеризует относительный прирост наращенной суммы за бесконечно малый промежуток времени. Она может быть постоянной или изменяться во времени. Постоянная сила роста. Как было показано выше, при дискретном начислении процентов т раз в году по номинальной ставке j наращенная сумма находится как 5= Р w1 т Чем больше /и, тем меньше промежуток между моментами начисления процентов. В пределе при т -» » имеем 5= /Mim 1 +-Ч ВАЛ где е — основание натуральных логарифмов. Для того чтобы отличить непрерывную ставку от дискретной, обозначим силу роста как 6. Теперь можно записать S = РеЬп.(3.26) Итак, при непрерывном наращении процентов наращенная :умма равна конечной величине, зависящей от первоначальной :уммы, срока наращения и силы роста. Последняя представляет собой номинальную ставку сложных процентов при т -**> 61   Легко показать, что дискретные и непрерывные ставки наращения находятся в функциональной зависимости. Из равенства множителей наращения(1 + 0я = еЬп следует: 6 = 1п(1 + 0, (3.27) /=€*-!. (3.28) ПРИМЕР 3.16. Сумма, на которую начисляются непрерывные проценты, равна 2 млн руб., сила роста 10%, срок 5 лет. Наращенная сумма составит S = 2 000 000 х е0'1*5 = 3297744,25 руб. Непрерывное наращение по ставке = 10% равнозначно наращению за тот же срок дискретных сложных процентов по годовой ставке. Находим /zzeo1 - 1 =0,10517. В итоге получим S = 2 000 000(1 + 0.10517)5 = 3297744,25 руб. Дисконтный можитель на основе силы роста (математическое дисконтирование) находится элементарно, для этого решим (3.26) относительно Р: Р = Se-*n.(3.29) Дисконтный множитель, как видим, равен е"*". ПРИМЕР 3.17. Определим современную стоимость платежа из примера 3.11 при условии, что дисконтирование производится по силе роста 12% и по дискретной сложной учетной ставке такого же размера. Получим в тыс. руб.: Р = 5000е-°'12х5 = 2744, Р = 5000(1 -0,12)5 = 2639. Переменная сила роста. Пусть сила роста изменяется во времени, следуя некоторому закону, представленному в виде не- 62 прерывной функции времени: 6, = /(*). Тогда наращенная сумма и современная величина определяются как S - Ре9; /> « 5е • . Функция времени может быть самого различного вида. Рассмотрим только два ее варианта — линейную и экспоненциальную. Начнем с линейной функции: 6,-6 + at, где 6 — начальное значение силы роста, а — прирост силы роста в единицу времени. Нетрудно доказать, что an Т J&tdt -|(б + д/)л - 8л + о о Таким образом, множитель наращения находится как  6Я 4Я - е 2 . (3.30) ПРИМЕР 3.18. Пусть начальное значение силы роста равно 8%, процентная ставка непрерывно и линейно изменяется, прирост за год составляет 2% (а = 0,02). Срок наращения 5 лет. Для расчета множителя наращения (3.30) найдем его степень: 0,02 х 52 0,08 х 5 + -*— = 0,65. Искомый множитель составит q = е0,65 = 1,91554. Продолжим пример. Предположим, что сила роста линейно уменьшается (пусть а = -0,02). В этом случае степень множителя равна 0,15 и соответственно q = е015 = 1,16183. Рассмотрим ситуацию, когда сила роста изменяется экспоненциально (по геометрической прогрессии): &, = 6я<, где б — начальное значение силы роста, а — постоянный темп роста. 63  В этом случае степень множителя равнао lnfl' а сам множитель находится как1 Я-*]па[ ■(3.31) ПРИМЕР 3.19. Начальный уровень силы роста 8%, процентная ставка непрерывно и экспоненциально увеличивается (годовой прирост 20%t a = 1,2), срок наращения 5 лет. Необходимо определить множитель наращения. Степень этого множителя за весь срок равна 0,8 -j^y(1f25 - 1) = 0,65305, соответственно q = в065305 = 1,92139. Срок ссуды и размер силы роста. Срок ссуды при постоянной силе роста найдем на основе (3.26): я=г- При наращении с изменяющейся силой роста (с постоянным темпом роста а) на основе (3.31) получим In п = — lngx ln(5/ Р) В свою очередь при наращении с постоянной силой роста \n(S/ P) 6 = п При наращении с изменяющейся с постоянным темпом силой роста lngx ln(5/ P) 6 ап - 1 1 См. Математическое приложение к главе. 64 Математическое приложение к главе Доказательство формулы (3.31) fba'dt Определим степень множителя наращения q « e°  ГЬа'Ш «6 —i\na о I Ina Inaj lna\I ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
