Финансовая математика. Тема Простые проценты

• Название: Тема Простые проценты
• Дата: 30.10.2022
• Размер: 0.99 Mb.
• Имя файла: Финансовая математика.docx
• Тип: Документы; #761756
• страница: 1 из 6

Тема 1. Простые проценты

Вопрос 1. Время как фактор стоимости в финансовых и коммерческих расчетах и его учет с помощью процентных ставок. Формула наращения по простым процентам. Простые проценты и процентные ставки. Практика начисления простых процентов.

В финансовых операциях одним из основных факторов? определяющих её результат, является фактор времени, который можно сформулировать как принцип неравноценности денег. Смысл этого принципа состоит в том, что одинаковые суммы сегодня и через любой промежуток времени неравноценны. Введем ряд переменных и определим основные понятия.

Под наращением начальной суммы будем понимать процесс её увеличения путем присоединения к ней начисленных процентов. Сумму, найденную наращиванием, называют наращенной суммой. Проценты, или процентные деньги – это абсолютная величина дохода от предоставления денег в долг на определенное время.

Используем следующие обозначения:

·     n – срок долга (в годах) или количество периодов начисления процентов;

·     P – первоначальная сумма, предоставленная в долг;

·     S – наращенная сумма;

·     i– процентная ставка (наращения);

·     d – учетная ставка.

Процентная ставка i за период начисления – это отношение дохода (разности между наращенной суммой и первоначальной суммой) к сумме вложенных средств: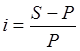 

.           (1) 

Если период начисления измеряется в годах, то i – годовая процентная ставка. Иначе она определяется периодом начисления (квартал, месяц, неделя, день и т.д.).

Из соотношения (1) можно выразить наращенную сумму S: 

.                  (2) 

Наращенную сумму можно также представить в виде первоначальной суммы и суммы процентов: 

.            (3) 

,               (4)

где

I– сумма начисленных процентов.

Процентная ставка называется простой, если в каждом периоде база для начисления процентов остается постоянной.

Пусть в момент размещения суммы P на банковском счете, единица измерения времени составила 1 год. И как следует из (4), проценты за первый год вклада равны I₁=i×P.

Согласно определению простой процентной ставки, проценты за каждый год вклада одинаковы и равны: 

.                (5) 

Накопленные проценты за весь срок вклада n лет составят: 

.            (6) 

Тогда наращенная сумма вклада через n лет станет равной: 

, 

или 

.           (7) 

В случае, если n не является целым числом, то нормальная коммерческая практика по отношению к дробным периодам года заключается в платеже процентов на пропорциональной основе. Это позволяет рассматривать выражения (6) и (7) как применимые ко всем неотрицательным значениям n. Ставка процентов обычно устанавливается в расчете за год, поэтому при продолжительности ссуды менее года необходимо выяснить, какую часть годовой процентной ставки следует выплатить. Для этого величину n выражают в виде дроби: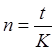 

,                (8) 

где

t – продолжительность финансовой операции (ссуды) в днях;

К– число дней в году (временная база).

Возможно несколько вариантов расчета процентов, различающихся выбором временной базы K и способом измерения срока пользования ссудой. Обычно за базу измерения времени берут год, условно состоящий из 360 дней (12 месяцев по 30 дней в каждом). В этом случае говорят, что вычисляют обыкновенный или коммерческий процент. В отличие от него точный процент получают, когда за базу берут действительное число дней в году: 365 или 366.

Определение числа дней также может быть точным или приближенным. В первом случае вычисляют фактическое число дней между двумя датами, во втором – продолжительность ссуды определяется числом месяцев и дней ссуды, приближенно считая все месяцы равными, содержащими по 30 дней. В обоих случаях дата выдачи и дата погашения долга считается за один день. Для подсчета точного числа дней между двумя датами можно воспользоваться специальной таблицей, в которой представлены порядковые номера дат в году.

Комбинируя различные варианты временной базы и методов подсчета дней ссуды, получаем три способа расчета процентов, применяемые на практике:

1.  (365/365) точные проценты с точным числом дней ссуды – британский;

2.  (365/360) обыкновенные проценты с точным числом дней ссуды – французский;

3.  (360/360) обыкновенные проценты с приближенным числом дней ссуды – германский.

Вопрос 2. Простые переменные ставки. Реинвестирование по простым процентам. Дисконтирование и учет по простым ставкам. Сопоставление ставки наращения и учетной ставки.

Из формулы (7) наращивания по простой процентной ставке можно определить величину множителя наращения: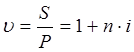 

.          (9) 

Множитель наращения (множитель накопления) - это число, показывающее во сколько раз наращенная сумма больше начальной суммы.

Процентные ставки, как правило, не остаются неизменными во времени, поэтому в кредитных соглашениях могут предусматриваться дискретно изменяющиеся во времени процентные ставки.

В этом случае формула расчета наращенной суммы принимает следующий вид: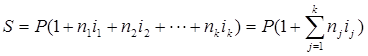 

.          (10) 

Дисконтирование и учет по простым ставкам.

В практике часто приходится решать задачу обратную наращению процентов, когда по заданной сумме S, соответствующей концу финансовой операции, требуется найти исходную сумму P. Расчет P по S называется дисконтированием суммы S. Величину P, найденную дисконтированием, называют современной величиной (текущей стоимостью) суммы S.

Разность в виде: 

,           (11) 

называют дисконтом или скидкой. Процесс начисления и удержания процентов вперед (в виде дисконта) называют учетом. Дисконт как скидка с конечной суммы долга может определяться через процентную ставку или в виде абсолютной величины.

В финансовых контрактах фактор времени чаще всего учитывается с помощью операции дисконтирования. Величина P эквивалентна сумме S в том смысле, что через определенный период времени и при заданной ставке процентов величина P в результате наращения станет равной S. Поэтому операцию дисконтирования называют также приведением. Однако понятие приведения несколько шире, чем дисконтирование.

Приведение – это вычисление некоторой стоимостной величины на заданный момент времени. Если некоторая сумма приводится к более ранней дате, чем текущая, то применяется дисконтирование, если же речь идет о более поздней дате, то – наращение. Имеет место также два вида дисконтирования: математическое дисконтирование и банковский (коммерческий) учет.

Математическое дисконтирование. Этот вид дисконтирования представляет собой решение задачи, обратной наращению. Если в прямой задаче наращенная сумма равна:

,            

то в обратной задаче: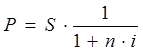

.                 

Дробь в правой части равенства при величине S называется дисконтным множителем. Этот множитель показывает, какую долю составляет начальная сумма в наращенной сумме. Дисконт определяется из соотношения (11).

Банковский или коммерческий учет. Операция учета (например: учета векселей) заключается в том, что кредитное учреждение (банк) до наступления срока платежа по векселю или другому платежному обязательству покупает его у владельца по цене ниже той суммы, которая предназначена к выплате в конце срока, т.е. приобретает, учитывает его с дисконтом.

Расчет процентов при банковском учете производится с помощью учетной ставки, которая мы обозначается символом d.

Простая учетная ставка определяется из соотношения: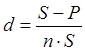 

.          (12) 

Отсюда: 

.            (13) 

Величина дисконта или учета равна: 

.                  (14) 

Следует заметить, что формула (13) справедлива, если срок n и учетная ставка d удовлетворяют условию nd < 1. Дисконтирование по простой учетной ставке применяют, как правило, в случае краткосрочных сделок, когда 0 < n ≤ 1 и 0 < d < 1.

Наращение по учетной ставке.

Учетная ставка может использоваться для наращения, т.е. для расчета S по P. В этом случае из формулы (13) следует: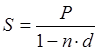 

.                 (15) 

Пример 1.годовая ном

В конце второго года сумма вклада составила 12000 рублей. Найти сумму процентов и величину начального вклада, если на него начислялась простая процентная ставка 25 % годовых.

Решение:

Согласно соотношению (6) сумма процентов составил n×i×P, а начальная сумма может быть получена из формулы (7).

Подставляя исходные данные находим: 



 

Пример 2.

Определить проценты и сумму накопленного долга, если ссуда равна 100000 руб. на срок 1,5 года, проценты простые по ставке 15 % годовых.

Решение:

Проценты за 1,5 года: I=Pni=100000·1,5·0,15=22500 руб.

Наращенная сумма: S=P+I = 100000+22500 = 122500 руб.

Пример 3.

В договоре, рассчитанном на год, принята ставка простых процентов на первый квартал в размере 12 % годовых, а на каждый последующий квартал на 1 % больше, чем в предыдущем. Определить множитель наращения за весь срок договора.

Решение:

Подставим исходные данные в формулу (9), учитывая соотношение (10):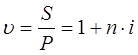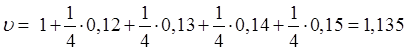 

. 

. 

Пример 4.

Через 140 дней должник уплатит 65 тысяч рублей. Кредит выдан под простые проценты 29 % годовых. Какова первоначальная сумма долга и дисконт при условии, что временная база равна 360 дней?

Решение: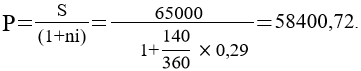

 

Пример 5.

Вексель учтен банком за n = 0,5 года до даты погашения по простой учетной ставке d= 20 %. Банк выплатил сумму Р = 18000 руб. Определить номинальную стоимость векселя.

Решение:

Номинальная стоимость векселя равна: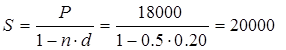 

. 

Пример 6.

Вексель на сумму 200000 руб. с датой погашения 27 ноября был учтен банком 11 августа по простой учетной ставке 32 % годовых. Продолжительность года 360 дней. Какая сумма будет выплачена банком?

Решение: 

t=20 +30+31+27 =108 дней. 



Пример 7.

Каким должен быть срок ссуды в днях, для того чтобы долг 100 тыс. руб., вырос до 120 тыс. руб. при условии, что начисляются простые проценты по ставке 25 % годовых? (К=365).

Решение:

По формуле простых процентов имеем: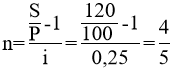 

.

Откуда: 

 

или в днях: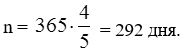

 

Пример 8.

Через какой срок вклад 30000 руб., при 20 % простых годовых будет равным 45000 руб.

Решение: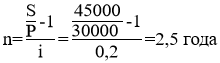 

. 

Пример 9.

Ссуда 25000 рублей выдана на 0,7 года под простые проценты 18 % годовых. Найти проценты и наращенную сумму.

Решение: 



 

Пример 10.

Вклад 20000 руб. через полгода, стал равным 22000 руб. Определить простую годовую процентную ставку.

Решение: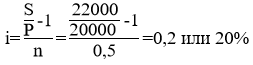 

. 

Пример 11.

Вексель учитывается банком за 120 дней до срока его погашения по простой учетной ставке 19 %. Найти доходность операции для банка в виде простой годовой процентной ставки (K=360).

Решение:

Из соотношений: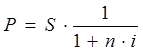 

. 

.

Имеем: 

 

n=120/360 = 0,3.

Из этого соотношения выразим i:

. 

Пример 12.

Сумма 2 млн руб. положена в банк 18 февраля не високосного года и востребована 25 декабря того же года. Ставка банка составляет 35 % годовых. Определить сумму начисленных процентов при различной практике их начисления.

Решение:

1.  Германская практика начисления простых процентов:

Временная база принимается за 360 дней, 

К=T = 360. 

Количество дней ссуды:

t = 11 (февраль) + 30 (март) + 30 (апрель) + 30 (май) + 30 (июнь) + 30 (июль) + 30 (август) + 30 (сентябрь) + 30 (октябрь) + 30 (ноябрь) + 25 (декабрь) - 1 = 305 дней.

Сумма начисленных процентов: 

 

2.  Французская практика начисления процентов:

Временная база принимается за 360 дней, 

К=T = 360.

 

Количество дней ссуды:

t = 11 (февраль) + 31 (март) + 30 (апрель) + 31 (май) + 30 (июнь) + 31 (июль) + 31 (август) + 30 (сентябрь) + 31 (октябрь) + 30 (ноябрь) + 25 (декабрь) - 1 = 310 дней.

По таблицам порядковых номеров дней в году можно определить точное число дней финансовой операции следующим образом: 

t = 359 - 49 = 310 дней. 

Сумма начисленных процентов: 

 

3.  Английская практика начисления процентов:

Временная база принимается за 365 дней, К=Т = 365.

Количество дней ссуды берется точным, t = 310 дней.

Сумма начисленных процентов: 

 

Пример 13.

Ссуда в размере 1 млн. руб. выдан 20 января до 5 октября включительно под 18%. Какую сумму должен заплатить должник в конце срока при начислении простых процентов? При решении использовать все три метода. Предварительно число дней ссуды: точное-258 дней, приближенное-255 дней.

Решение: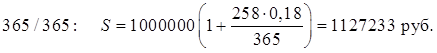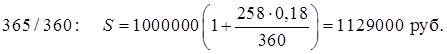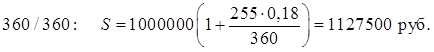

 

 

. 

Как видно, результат финансовой операции во многом зависит от выбора способа начисления простых процентов. Поскольку точное число дней в большинстве случаев больше приближенного числа дней, то и проценты с точным числом дней ссуды обычно получаются выше процентов с приближенным числом дней ссуды.

В практическом смысле эффект от выбора того или иного способа зависит от значительности сумм, фигурирующих в финансовой операции.