Финансовая математика. Тема Простые проценты
 Скачать 0.99 Mb. Скачать 0.99 Mb.
|
|
Тема 3. Финансовые ренты Вопрос 1. Виды платежей. Финансовые ренты. Основные параметры рент. Потоки платежей. Очень часто в контрактах финансового характера предусматриваются не отдельные разовые платежи, а серия платежей, распределенных во времени. Примерами могут быть регулярные выплаты с целью погашения долгосрочного кредита вместе с начисленными на него процентами, периодические взносы на расчетный счет, на котором формируется некоторый фонд различного назначения (инвестиционный, пенсионный, страховой, резервный, накопительный и т.д.), дивиденды, выплачиваемые по ценным бумагам, выплаты пенсий из пенсионного фонда и пр. Ряд последовательных выплат и поступлений называют потоком платежей. Выплаты представляются отрицательными величинами, а поступления - положительными. Обобщающими характеристиками потока платежей являются наращенная сумма и современная величина. Каждая из этих характеристик является числом. Наращенная сумма потока платежей – это сумма всех членов последовательности платежей с начисленными на них процентами к концу срока ренты. Под современной величиной потока платежей понимают сумму всех его членов, дисконтированных (приведенных) на некоторый момент времени, совпадающий с началом потока платежей или предшествующий ему. Конкретный смысл этих обобщающих характеристик определяется природой потока платежей, причиной, его порождающей. Например, наращенная сумма может представлять собой итоговый размер формируемого инвестиционного или какого-либо другого фонда, общую сумму задолженности. Современная величина может характеризовать приведенную прибыль, приведенные издержки. Финансовые ренты (аннуитеты). Поток платежей, все члены которого положительные величины, а временные интервалы постоянны, называют финансовой рентой или аннуитетом. Финансовая рента имеет следующие параметры: · член ренты – величина каждого отдельного платежа; · период ренты – временной интервал между двумя соседними платежами, срок ренты – время, измеренное от начала финансовой ренты до конца ее последнего периода; · процентная ставка – ставка, используемая при наращении или дисконтировании платежей, образующих ренту, число платежей в году; · число начислений процентов в году, моменты платежа внутри периода ренты. Виды финансовых рент. Классификация рент может быть произведена по различным признакам. В зависимости от продолжительности периода, ренты делят на годовые и p-срочные, где p - число выплат в году. По числу начислений процентов различают ренты с начислением один в году, m раз или непрерывно. Моменты начисления процентов могут не совпадать с моментами рентных платежей. По величине членов различают постоянные (с равными членами) и переменные ренты. Если размеры платежей изменяются по какому-либо математическому закону, то часто появляется возможность вывести стандартные формулы, значительно упрощающие расчеты. По вероятности выплаты членов различают ренты верные и условные. Верные ренты подлежат безусловной выплате, например, при погашении кредита. Выплата условной ренты ставится в зависимость от наступления некоторого случайного события. Поэтому число ее членов заранее неизвестно. Например, число выплат пенсий зависит от продолжительности жизни пенсионера. По числу членов различают ренты с конечным числом членов или ограниченные и бесконечные или вечные. В качестве вечной ренты можно рассматривать выплаты по облигационным займам с неограниченными или не фиксированными сроками. В зависимости от наличия сдвига момента начала ренты по отношению к началу действия контракта или какому-либо другому моменту ренты подразделяются на немедленные и отложенные или отсроченные. Срок немедленных рент начинается сразу, а у отложенных запаздывает. Ренты различают по моменту выплаты платежей. Если платежи осуществляются в конце каждого периода, то такие ренты называются обычными или постнумерандо. Если же выплаты производятся в начале каждого периода, то ренты называются пренумерандо. Иногда предусматриваются платежи в середине каждого периода. Анализ потоков платежей в большинстве случаев предполагает расчет наращенной суммы или современной величины ренты. Вопрос 2. Формулы для наращенной суммы и современной величины обычной годовой ренты постнумерандо и пренумерандо. Пусть в конце каждого года в течение n лет на расчетный счет вносится по R рублей, проценты начисляются один раз в года по ставке i. В этом случае первый взнос к концу срока ренты возрастет до величины R(1+i)n-1, так как на сумму R проценты начислялись в течение n-1 года. Второй взнос увеличится до R(1+i)n-2 и т.д. На последний взнос проценты не начисляются. Таким образом, в конце срока ренты ее наращенная сумма будет равна сумме членов геометрической прогрессии: в которой первый член равен R, знаменатель (1+i), число членов n. Эта сумма равна: где 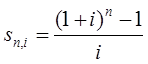 , (85) , (85)называется коэффициентом наращения ренты. Он зависит только от срока ренты n и уровня процентной ставки i. Пример 1. В фонд ежегодно в конце года поступают средства по 100000 руб. в течение 5 лет, на которые начисляют проценты по ставке 15 % годовых. Найти величину фонда на конец срока. Решение: 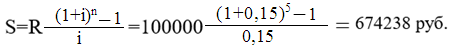 Годовая рента, начисление процентов m раз в году. Предположим теперь, что платежи делают один раз в конце года, а проценты начисляют m раз в году. Это означает, что применяется каждый раз ставка j/m, где j – номинальная ставка процентов. Тогда члены ренты с начисленными до конца срока процентами имеют вид: 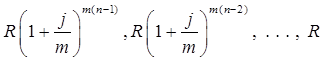 . .Если прочитать предыдущую строку справа налево, то нетрудно увидеть, что перед нами опять геометрическая прогрессия, первым членом которой является R, знаменателем (1+j/m)m, а число членов n. Сумма членов этой прогрессии и будет наращенной суммой ренты. Она равна: 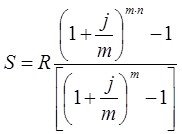 . (86) . (86)Пример 2. В фонд ежегодно в конце года поступают средства по 100000 руб. в течение трех лет, на которые начисляют проценты по ставке 15 % годовых, причем проценты начисляются поквартально. Найти величину фонда на конец срока. Решение: По формуле (86) имеем: 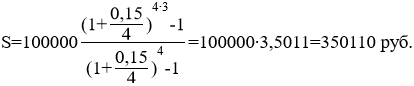 Рента p-срочная, . В контрактах часто начисление процентов и поступление платежа совпадают во времени. Таким образом число платежей p в году и число начислений процентов m совпадают, т.е. p=m. Тогда для получения формулы расчета наращенной суммы можно воспользоваться аналогией с годовой рентой и одноразовым начислением процентов в конце года, для которой: 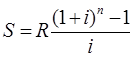 . .Различие будет лишь в том, что все параметры теперь характеризуют ставку и платеж за период, а не за год. Таким образом получаем: 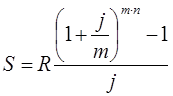 . (87) . (87)Пример 3. В течение 30 лет создается пенсионный фонд. На поступающие средства начисляются сложные проценты по ставке 8,5 %. Сумма годовых взносов составляет 200 тыс. руб. Определить величину фонда на конец срока, если взносы и начисление процентов производятся поквартально. Решение: По формуле (87) имеем: 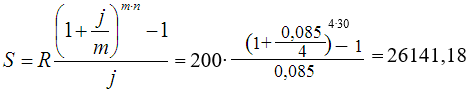 . .Рента p-срочная, p≥1, m≥1. Это самый общий случай p-срочной ренты с начислением процентов m раз в году, причем, возможно p≥m. Наращенная сумма: 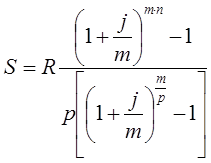 . (88) . (88)Отметим, что из нее легко получить все рассмотренные выше частные случаи, задавая соответствующие значения p и m. Пример 4. В фонд ежегодно в конце года поступают средства по 50000 руб. в течение семи лет, на которые начисляют проценты по ставке 15 % годовых, причем выплаты производятся поквартально, а проценты начисляются ежемесячно. Найти коэффициент наращения ренты и величину фонда на конец срока. Решение: Коэффициент наращения рент находят по формуле: 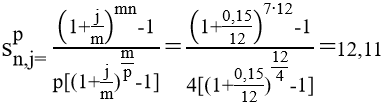 . .Наращенная сумма: Формулы современной величины. Обычная годовая рента: · А – современная величина ренты. 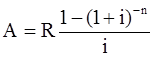 . (89) . (89)Коэффициент приведения ренты зависит только от двух параметров: срока ренты n и процентной ставки i. Поэтому его значения могут быть представлены в табличном виде. Такие таблицы можно найти в книгах или построить самим на компьютере. Рента p-срочная, p≥1, m≥1. Аналогичные рассуждения позволяют получить формулу для расчета современной величины ренты в самом общем случае для произвольных значений p и m: 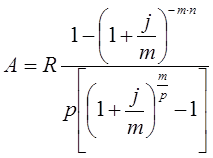 , (90) , (90)от которой нетрудно перейти к частным случаям при различных p и m. Пример 5. В фонд ежегодно в конце года поступают средства по 50000 руб. в течение семи лет, на которые начисляют проценты по ставке 15 % годовых, причем выплаты производятся и проценты начисляются ежеквартально. Найти современную стоимость фонда. Решение:____Пример_8.'>Решение: 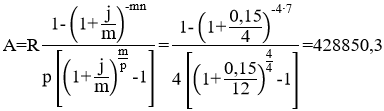 . .Рента пренумерандо. Рассмотрим теперь ренту, когда платежи производятся в начале каждого периода, – ренту пренумерандо. Различие между рентой постнумерандо и рентой пренумерандо заключается лишь в том, что у последней на один период начисления процентов больше. В остальном структура потоков с одинаковыми параметрами одинакова. Поэтому наращенные суммы обоих видов рент (с одинаковой периодичностью платежей и начисления процентов и размером выплат) тесно связаны между собой. Если обозначить через наращенную сумму ренты пренумерандо, а через S, как и раньше, наращенную сумму соответствующей ренты постнумерандо, то в самом общем случае получим: 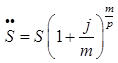 . (91) . (91)Точно также для современной величины ренты пренумерандо и соответствующей ей ренты постнумерандо имеем следующее соотношение: 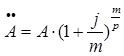 . (92) . (92)Пример 6. Инвестиции производятся на протяжении 4 лет один раз в конце года по 2 млн руб. Ставка сложных процентов 17 % годовых. Найти сумму инвестиций к концу срока. Решение: Наращенная сумма инвестиций: 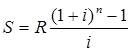 . .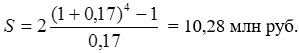 Пример 7. В течение 3 лет на расчетный счет в конце каждого года поступает по 10 млн руб., на которые начисляются проценты по сложной годовой ставке 10 %. Требуется определить сумму на расчетном счете к концу указанного срока. Решение: 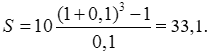 Пример 8. Найти наращенную сумму годовой ренты, если проценты начисляются по номинальной ставке 16 % ежемесячно, член ренты 50000 руб., срок ренты 4 года. Решение: 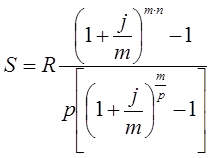 . .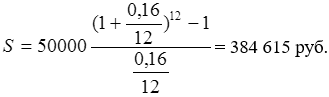 Пример 9. В течение 3 лет на расчетный счет в конце каждого года поступает по 10 млн руб., на которые начисляются проценты по сложной годовой ставке 10 %. Требуется определить сумму на расчетном счете к концу указанного срока. Решение: 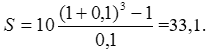 Пример 10. Бизнесмен арендовал виллу за 10 000 долларов в год. Какова выкупная цена аренды при годовой ставке процента 5 %? Решение: Выкупная цена есть современная величина всех будущих арендных платежей и равна: Пример 11. Инвестиции в проект к концу первого года его реализации составят 10000 руб. В последующие три года ожидаются годовые доходы по проекту 3000 руб., 4200 руб., 6800 руб. Издержки привлечения капитала 10 %. Рассчитать чистую текущую стоимость проекта. Решение: В данной задаче применяем формулу расчета наращенной суммы постоянной ренты пренумерандо: 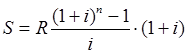 . .Так как 10000 руб. – вложенные деньги, то будем их учитывать со знаком «-»: Пример 12. В фонд ежегодно в конце года поступают средства по 50000 руб. в течение 7 лет, на которые начисляют проценты по ставке 15 % годовых, причем выплаты производят поквартально, а проценты начисляются ежемесячно. Определить коэффициент наращения ренты и величину фонда на конец срока. Решение: Коэффициент наращения ренты находят по формуле: 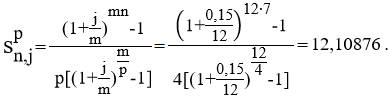 Наращенная сумма: Пример 13. Вкладчик в течение 5 лет ежегодно вносит в банк R =100000 руб. Проценты на вклад начисляются по сложной процентной ставке i=15 % годовых. Найти наращенную сумму и современную величину ренты пренумерандо. Решение:  . .Определение параметров финансовой ренты. Иногда при разработке контрактов возникает задача определения по заданной наращенной сумме ренты S или ее современной стоимости A остальных параметров ренты: R, n, i, p, m. Такие параметры как m и p обычно задаются по согласию двух подписывающих сторон. Остаются параметры R, n, i. Два из них задаются, а третий рассчитывается. Такие расчеты могут быть неоднократно повторены при различных значениях задаваемых параметров, пока не будет достигнуто согласие сторон. Определение размера ежегодной суммы платежа R в зависимости от того какая обобщающая характеристика постоянной ренты задана S или A, возможны два варианта расчета: 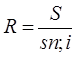 , (93) , (93)или 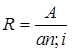 . (94) . (94)Пример 14. В фонд ежегодно в конце года поступают средства по 100000 руб. в течение 7 лет, на которые начисляют проценты по ставке 15 % годовых. Найти коэффициент приведения ренты и современную стоимость фонда. Решение: Коэффициент приведения ренты находится по формуле: 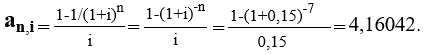 Современная стоимость определяется соотношением: Пример 15. В фонд ежегодно в конце года поступают средства в течение 7 лет, на которые начисляют проценты по ставке 15 % годовых, причем выплаты производятся поквартально, а проценты начисляются ежемесячно. Наращенная сумма к концу срока составит 100 тысяч рублей. Определить коэффициент наращения ренты и годовую выплату. Решение: Коэффициент наращения ренты находится по формуле: 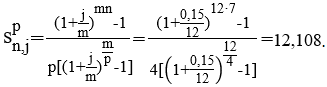 Наращенная стоимость ренты определяется соотношением: Определение срока постоянной ренты. Рассмотрим решение этой задачи на примере обычной годовой ренты с постоянными заданными платежами. Решая исходные формулы для S и A: 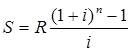 , ,или Относительно срока n, получаем соответственно следующие два выражения: 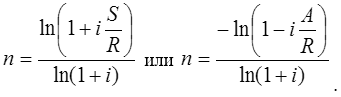 (95) (95)Последнее выражение, очевидно, имеет смысл только при R>Ai. Пример 16. Долг в размере 300000 рублей погашается равными частями в конце каждого года по ставке 12 % годовых, причем размер ежегодных выплат R=50000 руб. Определить время погашения долга. Решение: Для ренты постнумерандо: 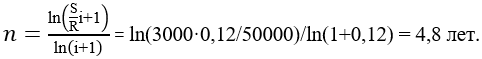 Определение ставки процентов. Для того, чтобы найти ставку i, необходимо решить одно из нелинейных уравнений (предполагаем, что речь идет о постоянной годовой ренте постнумерандо) следующего вида: 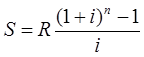 , ,или 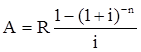 , ,которые эквивалентны двум другим: 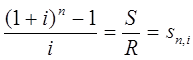 , ,или 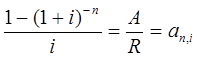 . (96) . (96)В этих уравнениях единственным неизвестным является процентная ставка i. Решение нелинейных уравнений может быть найдено лишь приближенно. Известно несколько методов решения таких уравнений: · метод линейной интерполяции; · метод Ньютона-Рафсона и др. Мы рассмотрим сначала первый из них. Метод линейной интерполяции. Прежде всего нужно найти с помощью прикидочных расчетов нижнюю (iн) и верхнюю (iв) оценки ставки. Это осуществляется путем подстановки в одну из формул (97) различных числовых значений i и сравнения результата с правой частью выражения. Далее корректировка нижнего значения ставки производится по следующей интерполяционной формуле: 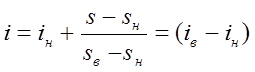 , (97) , (97)в которой sви sн– значения коэффициента наращения (или коэффициента приведения) ренты для процентных ставок iни iвсоответственно. Полученное значение ставки проверяют, подставляя его в левую часть исходного уравнения и сравнивая результат с правой частью. Если достигнутая точность недостаточна, повторно применяют формулу (97), заменив в ней значение одной из приближенных оценок ставки на более точное, найденное на предыдущей итерации, и соответствующее ей значение множителя наращения (или приведения). Метод Ньютона-Рафсона. В этом методе решение также находят итеративно, постепенно шаг за шагом уточняя оценку. В общем случае метод Ньютона-Рафсона состоит в последовательном приближении к решению х0 нелинейных уравнений вида: В нашем конкретном случае алгоритм поиска сводится к трем операциям на каждом шаге, которые зависят от постановки задачи (задана S или A) и типа ренты. Сначала будем считать, что известна наращенная сумма S и найдена какая-то начальная оценка процентной ставки (например, методом проб). а) Постоянная годовая рента постнумерандо, проценты начисляются один раз в конце года, p=1, m=1. Требуется решить уравнение вида: 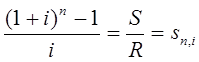 , ,или 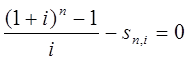 . .Если ввести обозначение q=1+i и умножить обе части уравнения на –(q-1), то получим алгоритм уточнения оценки на каждом шаге k, состоящий из следующих трех операций: 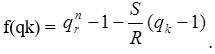 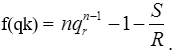 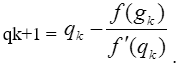 б) Постоянная p-срочная рента постнумерандо, проценты начисляются один раз в конце года, p≥1, m=1. Требуется решить уравнение вида: 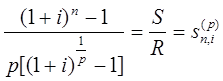 , ,или 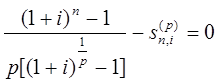 . .Вновь используем обозначение q=1+i и получим алгоритм уточнения оценки на каждом шаге k, состоящий из следующих трех операций: 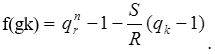 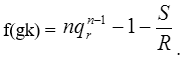 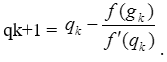 Замечания: 1. Начальную оценку q0=1+i0, требующуюся для начала итеративной процедуры, следует выбирать такой, чтобы соответствующий ей множитель наращения был как можно ближе к заданному отношению S/R. Это сократит число итераций и обеспечит сходимость алгоритма. 2. Остановка вычислений осуществляется после того как проверка, заключающаяся в сравнении множителя наращения и отношения S/R, свидетельствует об их совпадении с достаточной (наперед заданной) точностью. Теперь будем считать, что известна современная стоимость A и найдена какая-то подходящая начальная оценка процентной ставки: а) Постоянная годовая рента постнумерандо, проценты начисляются один раз в конце года, p=1, m=1. Требуется решить уравнение вида: 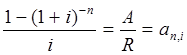 , ,или 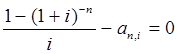 . .Здесь также используем обозначение q=1+i и после умножения обеих частей равенства на (q-1), то получим алгоритм уточнения оценки на каждом шаге k, состоящий из следующих трех операций: 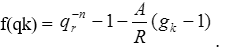 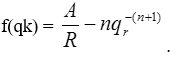 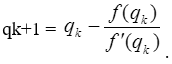 б) Постоянная p-срочная рента постнумерандо, проценты начисляются один раз в конце года, p≥1, m=1. Требуется решить уравнение вида: 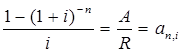 , ,или 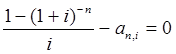 . .Сделав подстановку q = 1+i, получим алгоритм уточнения оценки на каждом шаге k, состоящий из следующих трех операций: 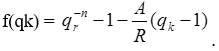 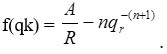 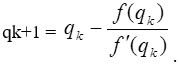 Вопрос 3. Эквивалентные платежи. Принцип эквивалентности. Консолидация(объединение) потока платежей в один. Уравнение эквивалентности. Эквивалентные платежи. Принцип эквивалентности. В практике часто возникает необходимость в изменении условий контракта: например, должник может попросить об отсрочке срока погашения долга или, напротив, изъявить желание погасить его досрочно, в ряде случаев может возникнуть потребность объединить (консолидировать) несколько долговых обязательств в одно и т.д. Во всех этих случаях применяется принцип финансовой эквивалентности старых (заменяемых) и новых (заменяющих) обязательств. Для решения задач по изменению условий контракта разрабатывается так называемое уравнение эквивалентности, в котором сумма заменяемых платежей, приведенных к какому-либо одному моменту времени, приравнивается сумме платежей по новому обязательству, приведенных к той же дате. При этом соблюдается неизменность финансовых отношений сторон до и после заключения контрактов или, как говорят финансовая эквивалентность, обязательств. Расчет платежей в этом случае базируется на уравнении эквивалентности. Уравнением эквивалентности называется равенство сумм заменяемых и заменяющих платежей, приведенных к одному моменту времени. Принцип финансовой эквивалентности позволяет сравнивать два отдельных платежа в различные моменты времени. При оценке этих платежей сравнивают их современные стоимости и тот платеж считается большим, у которого современная стоимость больше. Пример 17. Первый платеж в 90000 рублей должен быть выплачен через 30 дней, а второй, равный 92 000 рублей, - через 270 дней. Сравнить эти платежи при простой процентной ставке 15 %, К = 360. Решение: Современная стоимость первого платежа: 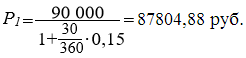 Современная стоимость второго платежа: 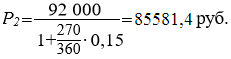 При заданной ставке первый платеж превышает второй. Для краткосрочных контрактов применяются простые процентные ставки, а для средне- и долгосрочных – сложные ставки. При определении срока консолидированного платежа уравнение эквивалентности представляют как равенство современных стоимостей заменяемых и консолидированного платежей. Уравнение эквивалентности для простых процентов: 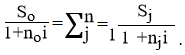 (98) (98)Если сумму в правой части обозначить через n, то решение эквивалентности относительно n0 имеет вид: 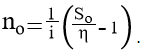 (99) (99)Аналогично для сложных процентов: 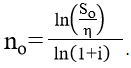 (100) (100)Пример 18. Три платежа: 200 тыс. руб. со сроком 2 года, 400 тыс. руб. со сроком 3 года 300 тыс. руб. со сроком 4 года заменяются одним – в размере 800 тыс. руб. Стороны договорились об использовании сложной процентной ставки 18 % годовых. Определить срок консолидированного платежа. Решение: При определении современной стоимости заменяемых платежей найдем n по формуле сложных процентов: 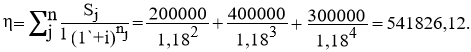 Срок консолидированного платежа равен: 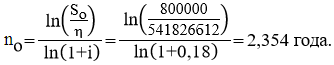 Консолидация (объединение) потока платежей в один. Уравнение эквивалентности. В случае с объединением (консолидированием) нескольких платежей в один сумма заменяемых платежей, приведенных к одной и той же дате, приравнивается к новому обязательству: где tj – временной интервал между сроками, tj=n0-nj. Пример 19. Решено консолидировать два платежа со сроками 20.04 и 10.05 и суммами платежа 20 тыс. руб. и 30 тыс. руб. Срок консолидации платежей 31.05. Определить сумму консолидированного платежа при условии, что ставка равна 10 % годовых. Решение: Определим временной интервал между сроками для первого платежа и консолидированного платежа:[1] t1= 11(апрель) + 31(май) - 1 = 41 день, для второго платежа и консолидированного платежа: t2 = 22(май) - 1 = 21 день. Отсюда сумма консолидированного платежа Sоб будет равна: 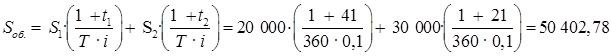 . .Таким образом, консолидированный платеж со сроком 31.05 составит 50 402,78 руб. Пример 20. Три платежа: 200 тыс. руб. со сроком 2 года, 400 тыс. руб. со сроком 3 года 300 тыс. руб. со сроком 4 года заменяются двумя, причем через год выплачивается 200 тыс. руб., а остаток – через 5 лет. Перерасчет осуществляется по сложной процентной ставке 25 % годовых. Определить остаток долга. Решение: Запишем уравнение эквивалентности: 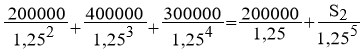 . .Отсюда находим остаток S2. Пример 21. Три платежа: 200 тыс. руб. со сроком 2 года, 400 тыс. руб. со сроком 3 года 300 тыс. руб. со сроком 4 года заменяются двумя с выплатами 200 тыс. руб. через 1 год и 850 тыс. руб. Перерасчет осуществляется по сложной процентной ставке 25 % годовых. Определить срок выплаты суммы 850 тыс. руб. Решение: Уравнение эквивалентности имеет вид: Решая уравнение относительно n, получим: Конечно, существуют различные возможности изменения условий финансового соглашения, и в соответствии с этим многообразие уравнений эквивалентности. Готовыми формулами невозможно охватить все случаи, возникающие в практической деятельности, но в каждой конкретной ситуации при замене платежей уравнение эквивалентности составляется похожим образом. Если платеж S1 со сроком n1 надо заменить платежом Sоб. со сроком nоб. (nоб. > n1) при использовании сложной процентной ставки i, то уравнение эквивалентности имеет вид: Пример 22. Предлагается платеж в 45 тыс. руб. со сроком уплаты через 3 года заменить платежом со сроком уплаты через 5 лет. Найти новую сумму платежа, исходя из ставки 12 % годовых. Решение: Поскольку nоб. > n1, то платеж составит: Таким образом, в новых условиях финансовой операции будет предусмотрен платеж 56 448 руб. Вопрос 4. Рента с непрерывным начислением процентов. Рента с платежами, изменяющимися по закону геометрической прогрессии. Рента с платежами, изменяющимися по закону арифметической прогрессии. Рента с непрерывным начислением процентов. Формула для наращенной суммы ренты с непрерывным начислением процентов: 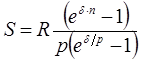 . (103) . (103)Формула для современной стоимости ренты с непрерывным начислением процентов: 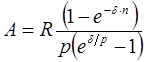 . (104) . (104)Пример 23. В фонд ежегодно в конце года поступают средства по 50000 рублей в течение 7 лет, на которые начисляют проценты по ставке 15 %, причем выплаты производятся поквартально, а проценты начисляются непрерывно. Определить коэффициенты наращения и приведения ренты, величину фонда на конец и начало срока ренты. Решение: Определим наращенную сумму и коэффициент наращения, современную стоимость коэффициент приведения ренты с непрерывным начислением процентов: 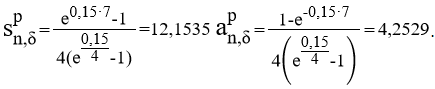 S=50000·12,1535=607679,2. A=50000·4,2529=212642,99. Вечная рента. Под вечной рентой понимается последовательность платежей, число членов которой не ограничено, то есть она выплачивается бесконечное число лет (например, выплаты по бессрочным облигационным займам). В этом случае наращенная сумма с течением времени возрастает бесконечно. А вот современная величина имеет вполне определенное конечное значение. Рассмотрим, например, бесконечную постоянную годовую ренту постнумерандо (p = 1, m = 1): 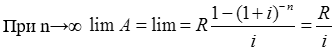 . (105) . (105)Пример 24. Требуется выкупить вечную ренту, член которой равен 5 млн рублей, выплачиваемых в конце каждого полугодия под 25 % годовых. Решение: Капитализированная стоимость такой ренты составит: 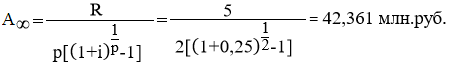 Отложенная рента. Начало отложенной (или отсроченной) ренты отодвигается от момента заключения сделки на какой-то момент в будущем. Наращенная сумма такой ренты может быть подсчитана по тем формулам, которые нам уже известны. А ее современную величину можно определить в два этапа: сначала найти современную величину соответствующей немедленной ренты (эта сумма характеризует ренту на момент начала ее срока), а затем с помощью дисконтирования этой величины по принятой ставке в течение срока задержки привести ее к моменту заключения договора. Например, если современная величина годовой немедленной ренты равна A, то современная величина отложенной на t лет ренты составит: где vt– дисконтный множитель за t лет, v=1/(1+i)<1. Пример 25. Спустя три года после образования фонда начинают поступать средства по 100000 руб. в конце каждого года в течение 7 лет, на которые начисляют проценты по ставке 15 % годовых. Найти современную стоимость и наращенную сумму фонда. Современная стоимость фонда определяется по формуле: 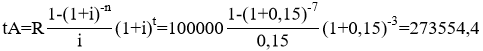 . .Наращенная сумма фонда определяется по формуле: 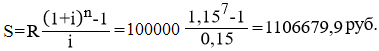 Рента с платежами в середине периодов. Наращенная сумма (S1/2) и современная стоимость (A1/2) ренты с платежами в середине периодов и соответствующей ренты постнумерандо связаны так: 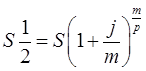 , ,и 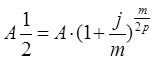 . (107) . (107)Наращенная сумма всей ренты: 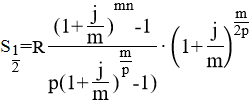 . .Пример 26. В фонд ежегодно в середине периода поступают средства по 100000 руб. в течение 7 лет, на которые начисляют проценты по ставке 15 % годовых, причем выплаты производят поквартально, а проценты начисляются ежемесячно. Определить наращенную сумму ренты и величину фонда на конец срока. Решение: Наращенная сумма ренты постнумерандо определяется по формуле: 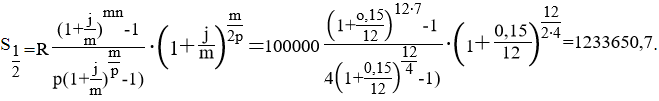 Современная стоимость ренты постнумерандо: 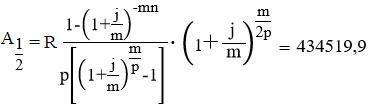 . .Рента с платежами, изменяющимися по закону геометрической прогрессии. Если платежи годовой ренты изменяются с постоянным темпом роста q, то члены ренты будут представлять собой ряд: R, Rq, … , Rq n-1. Величина t-го члена равна Rt=Rq t-1. Для того чтобы получить современную величину, дисконтируем эти величины: Мы получили геометрическую прогрессию. Наращенная сумма S равна: 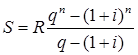 . (108) . (108)Рента с платежами, изменяющимися по закону арифметической прогрессии. Пусть размер платежей изменяется с постоянным приростом a (положительным или отрицательным), т.е. с платежами, изменяющимися по закону арифметической прогрессии. Если рента годовая постнумерандо, то размеры последовательных платежей составят R: Величина t-го члена равна Rt=R+(t-1)a. Тогда современная стоимость такой ренты равна: 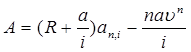 , (109) , (109)а наращенная сумма: 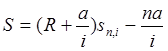 . (110) . (110)В случае p-срочной ренты с постоянным приростом платежей (m=1) последовательные выплаты равны: где a– прирост платежей за год; R– первый платеж, то есть Rt=R+(a×t-1); t– номер члена ряда, t=1, 2, … , np. Современная величина: 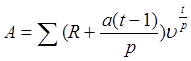 , (111) , (111)а наращенная сумма: 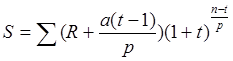 . (112) . (112)Пример 27. В долг берется 300000 руб. под годовую ставку 6 %. В год выплачивается по 34000 руб. Сколько лет займут эти выплаты? Решение: Пример 28. Предположим, что есть два варианта инвестирования средств в течение 4 лет: в начале каждого года под 26 % годовых или в конце каждого года под 38 % годовых. Пусть ежегодно вносится 300000 руб. Определить, сколько денег окажется на счете в конце 4-го года для каждого варианта. В данном случае производятся периодические платежи, и расчет ведется по формулам наращенной суммы постоянной ренты пренумерандо и наращенная сумма постоянной ренты постнумерандо. Решение: Для первого варианта: 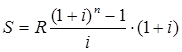 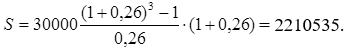 Для второго варианта: 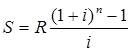 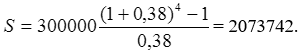 Пример 29. Два платежа S1 = 100 тыс. руб. и S2 = 50 тыс. руб. со сроками 150 и 180 дней, отсчитываемыми от одной базы, заменяются одним со сроком 200 дней. Стороны согласились на замену при использовании простой ставки, равной 6 % годовых. Найти величину консолидированного платежа S. Решение: Для замены ренты S1, S2 платежом S можно воспользоваться тем, что платеж S должен равняться сумме наращений выплат S1, S2 за период их отсрочки: 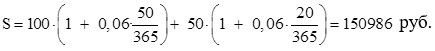 |
