Финансовая математика. Тема Простые проценты
 Скачать 0.99 Mb. Скачать 0.99 Mb.
|
|
Тема 2. Сложные проценты Вопрос 1. Формула наращения по сложным процентам. Процентная ставка называется сложной, если на каждом периоде начисления процентов исходной базой является наращенная сумма, полученная на предыдущем периоде. Присоединение начисленных процентов к сумме, которая служила базой для их определения, называют капитализацией процентов. Пусть P – начальная сумма, размещенная на банковском счете под i – сложную годовую процентную ставку. Тогда по определению сложной процентной ставки, базой для начисления процентов на каждом периоде является сумма, полученная на предыдущем периоде наращения. Следовательно, проценты и наращенные суммы за каждый год вклада составляют: Рассмотрим выражения для процентов: 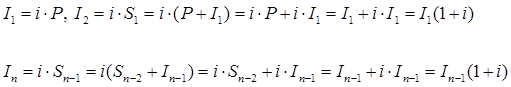 . . Следовательно, I1,I2,…In-1, Ln – члены геометрической прогрессии с первым членом I1 и знаменателем (1+i). Проценты за весь срок вклада составляют In=I1+I2+…+In-1+In. По формуле суммы n членов геометрической прогрессии находим: 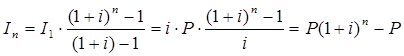 . (16) . (16)Наращенная сумма вклада через n лет станет равной начальному вкладу и сумме процентов – S=P+In, подставляя In из (16) получим: Особенностью сложных процентов является то, что при капитализации процентов, предыдущие проценты увеличивают будущие проценты. Такое нелинейное влияние сложных процентов на накопление может быть очень значительным, особенно если длительность начисления или процентная ставка достаточно велики. Пример 1. Вклад 50000 руб. помещен в банк на 2 года под 15 % годовых (проценты сложные). Найти наращенную сумму. Решение: Наращение по сложной переменной процентной ставке. В том случае, когда ставка сложных процентов меняется во времени, формула наращения имеет следующий вид: 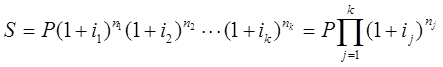 , (18) , (18) где Пример 2. Срок ссуды – 5 лет, договорная базовая процентная ставка 12 % годовых. В первые два года ставка увеличена на 0,5 % и на 0,75 % в оставшиеся года. Найти множитель наращения: ν = S/P. Решение: Проценты за 1,5 года: I=Pni=100000·1,5·0,15=22500 руб. Наращенная сумма: S=P+I = 100000+22500 = 122500 руб. Начисление сложных годовых процентов при дробном числе лет. При дробном числе лет проценты начисляются разными способами: 1. По формуле сложных процентов: 2. На основе смешанного метода, согласно которому за целое число лет начисляются сложные проценты, а за дробное – простые: где a – целое число лет; b – дробная часть года. 3. В ряде коммерческих банков применяется правило, в соответствии с которым за отрезки времени меньше периода начисления проценты не начисляются, т.е. Пример 3. Первоначальная сумма Р = 60000 руб. помещена в банк на срок 2,5 года под 20 % годовых. Найти наращенную сумму тремя способами. Решение: Найдем наращенную сумму тремя способами. 1. S=P(1+𝑖)𝑛 = 60000(1+0,2)2,5 = 94646,5 руб. 2. S=P(1+𝑖)[𝑎] (1+{𝑏}𝑖)=60000·(1+0,2)2 (1+0,5· 0,2)==95040 руб. 3. S=P(1+𝑖)𝑎= 60000·(1+0,2)2=86400 руб. Вопрос 2. Номинальная и эффективная ставки процентов. Непрерывное начисление процентов. Наращение суммы вклада по номинальной ставке. В случае, когда сложные проценты начисляются m раз в году, то годовую процентную ставку называют номинальной и обозначают j. При этом в каждый 1/m период года начисляются проценты по ставке . Если срок начисления процентов составил n – лет, то количество периодов начисления равно m×n и соотношение для начисления сложных процентов примет вид: 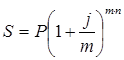 . (22) . (22)Пример 4. Первоначальная сумма составила Р = 6000 руб., период начисления n = 3 года, сложная процентная ставка i = 20 % начисляется ежеквартально m = 4. Найти наращенную сумму. Решение: Подставляя исходные данные в соотношение (22) получаем: 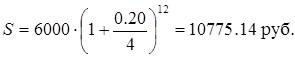 Пример 5. Первоначальная сумма Р = 700000 руб., период начисления n = 2 года, сложная процентная ставка j = 12 %, начисление процентов ежеквартально. Найти наращенную сумму. Решение: m = 4 (в году 4 квартала). Тогда наращенная сумма равна: S = P(1+j/m) mn = 700000·(1+0,12/4)2·4 = 886739 руб. Эффективная ставка показывает, какая годовая ставка сложных процентов дает тот же финансовый результат, что и m – разовое наращение в год по ставке j/m. Если проценты капитализируются m раз в год, каждый раз со ставкой j/m, то, по определению, можно записать равенство для соответствующих множителей наращения: где: iэ – эффективная ставка; j – номинальная ставка. Отсюда получаем, что связь между эффективной и номинальной ставками выражается соотношением: Пример 6. Вычислить эффективную ставку процента, если банк начисляет проценты ежеквартально, исходя из номинальной ставки 10 % годовых. Решение: 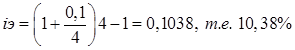 . . Пример 7. Первоначальная сумма вклада Р = 16000 руб. наращенная сумма составила S = 31250 руб., период начисления n = 3 года. Найти процентную ставку сложных процентов. Решение: 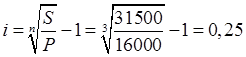 . . i = 25 %. Пример 8. К первоначальной сумме Р = 4000 рублей применялась сложная процентная ставка i1 = 25 % в течение первых двух лет n1 = 2, в следующие три года n2 = 3, i2 = 20 %, и последние два года n3 = 2, i3 = 15 %. Найти наращенную сумму. Решение: Подставляя исходные данные в формулу (18) получаем: Формула удвоения суммы. При прогнозировании инвестиционных возможностей в будущем часто необходимо решить задачу: через сколько лет сумма ссуды возрастет в N раз при данной процентной ставке. Ответ получим, приравняв множитель наращения величине N: а) для простых процентов: откуда: 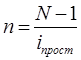 , (23) , (23) б) для сложных процентов: откуда: 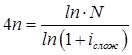 . (24) . (24) Особенно часто используется N = 2. Тогда формулы (23) и (24) называются формулами удвоения и принимают следующий вид: а) для простых процентов: 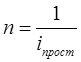 , (25) , (25) б) для сложных процентов: 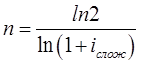 . (26) . (26) Если формулу (25) легко применять для прикидочных расчетов, то формула (26) требует применения калькулятора. Однако, при небольших ставках процентов (менее 10 %) вместо нее можно использовать более простую приближенную. Ее легко получить, если учесть, что тогда: 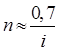 . (27) . (27) Пример 9. Рассчитать, за сколько лет долг увеличится вдвое при ставке простых и сложных процентов равной 10 %. Для ставки сложных процентов расчеты выполнить по точной и приближенной формуле. Результаты сравнить. Решение: а) При простых процентах: 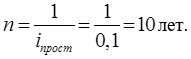 б) При сложных процентах и точной формуле: 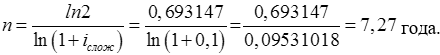 в) При сложных процентах и приближенной формуле: 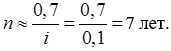 Выводы: 1. Одинаковое значение ставок простых и сложных процентов приводит к совершенно различным результатам. 2. При малых значениях ставки сложных процентов точная и приближенная формулы дают практически одинаковые результаты. Непрерывное начисление процентов. Непрерывное начисление процентов – это начисление процентов, при котором интервалы между начислениями стремятся к нулю, а количество начислений стремится к бесконечности. Большое значение непрерывное наращение имеет при решении сложных финансовых проблем, например, при анализе характеристик ценных бумаг. Число начислений m входит в соотношение (19) для наращенной суммы по номинальной процентной ставке. Определим предел этой суммы при бесконечном увеличении числа начислений, воспользовавшись известным из курса «Математического анализа» 2-м замечательным пределом: 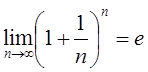 , , где е– основание натурального логарифма. 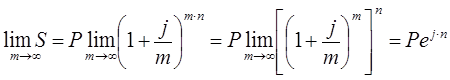 . . Для того, чтобы отличать ставку непрерывных процентов от ставок дискретных процентов, ее называют силой роста и обозначают символом δ. Таким образом: Пример 10. Первоначальная сумма составила Р = 7000 руб., период начисления n = 2 года, сила роста = 15 %. Найти наращенную сумму. Решение: Подставляя исходные данные в формулу (28) получаем: Начисление непрерывных процессов с переменной силой роста. Рассмотрим последовательность непрерывных ставок δ 1, δ 2, … δ k, которые соответствовали начислению процентов в течение n1, n2, …nk лет. Наращенные суммы за каждый период начисления равны: 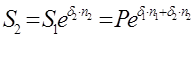 . . 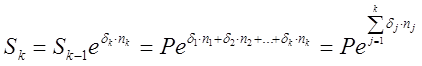 . .или где 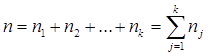 . . 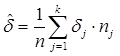 . . Пример 11. На вклад в 400 тыс. руб. начисляются непрерывные проценты. Найти наращенную сумму за 8 лет, если сила роста изменялась следующим образом: первые 3 года равна10 %, в следующе 2 года равна 12 %, в следующие 2 года равна 11 % и в последний год равна 14 %. Решение: 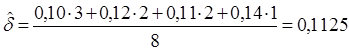 . . Пример 12. Первоначальная сумма P = 700000 руб., период начисления года, сложная процентная ставка δ = 12 % годовых. Начисление процентов происходит непрерывно. Найти наращенную сумму. Решение: Непрерывное изменение ставки непрерывных процентов. Ставка непрерывных процентов определена как функция зависящая от времени или В формуле (27) для дискретно изменяющейся ставки непрерывных процентов заменяем сумму, стоящую в показателе экспоненты на интеграл или: 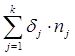 на на 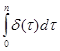 . . Наращенная сумма равна: 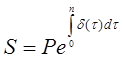 . (30) . (30) Пример 13. Найти наращенную сумму при начислении непрерывных процентов на сумму 200 тыс. руб. за 3 года, если значение силы роста изменяется по формуле Решение: Подставляем в формулу (30) исходные данные получаем: 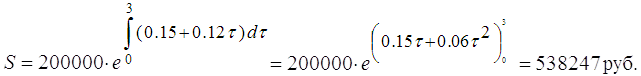 Вопрос 3. Наращивание и дисконтирование. Учет (дисконтирование) по сложной ставке процентов. Как и в случае простых процентов, рассмотрим два вида учета – математический и банковский. Математический учет представляет собой задачу обратную наращению по сложной процентной ставке. Формула наращения имеет вид: Выразим из формулы Р: 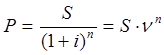 , (31) , (31) где 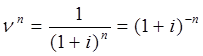 . (32) . (32) учетный или дисконтный множитель. При начислении процентов m в году по номинальной ставке j выражение для Р будет иметь вид: 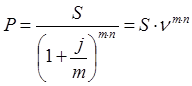 , (33) , (33) где 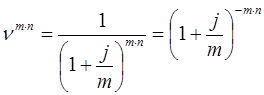 . (34) . (34) дисконтный множитель. Величину P, полученную дисконтированием S, называют современной или текущей стоимостью или приведенной величиной S. Суммы P и S эквивалентны в том смысле, что платеж в сумме S через n лет равноценен сумме P, выплачиваемой в настоящий момент. Разность D = S - P называется дисконтом. Пример 14. По вкладу сроком на 2 года по сложной ставке 12 % годовых была получена сумма 700000 руб. Рассчитать сумму, полученную заемщиком. Решение: 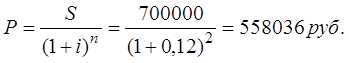 Банковский учет предполагает использование сложной учетной ставки. Дисконтирование по сложной учетной ставке выполнить по формуле: Дисконт в случае банковского учета равен: При использовании сложной учетной ставки процесс дисконтирования происходит с прогрессирующим замедлением, так как учетная ставка каждый раз применяется к сумме, уменьшенной за предыдущий период на величину дисконта. Пример 15. Долговое обязательство на сумму 200 тыс. руб. срок оплаты которого наступает через 4 года продается с дисконтом по сложной учетной ставке d = 12 % годовых. Каков размер полученной за долг суммы и величина дисконта? Решение: D = 200 000 ‑119 939 = 80 061. Дисконтирование по номинальной учетной ставке. Годовая учетная ставка f называется номинальной, если в течение года m раз проводится учет и применяется сложная учетная ставка . Дисконтирование по номинальной учетной ставке вычисляется по формуле: 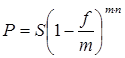 . (37) . (37)Пример 16. Вексель на сумму 200000 рублей учтен по сложной процентной ставке 18 % годовых, срок платежа наступает через 1,8 года. Определить сумму, полученную владельцем векселя при учете, и дисконт при ежегодном и ежемесячном дисконтировании. Решение: а) m = 1 P=S(1-d)n = 200000·(1−0,18)1,8= 139924,9 руб. D = S-P = 200000-139924,9 = 60075,1 руб. б) m=12 P=S·(1-f/m)mn = 200000·(1−0,18/12)(1,8·12) = 144295,43. D = 200000-144295,43 = 557054,57. Непрерывное дисконтирование по сложной учетной ставке. Непрерывное дисконтирование – это дисконтирование на бесконечно малых отрезках времени, поскольку при m → ∞, 1/m .Так как при непрерывном начислении процентов начало и конец периода начисления процентов совпадают, то номинальные процентные ставки j и f при m → ∞ перестают различаться. Действительно наращенная сумма равна: 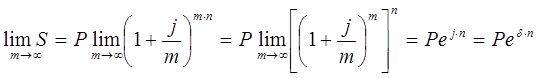 , ,а наращивание по номинальной дисконтной ставке: 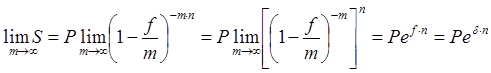 . .Поэтому при m → ∞ пользуются одной процентной ставкой – силой роста δ. Тогда при непрерывном дисконтировании справедлива формула: Вопрос 4. Расчет срока ссуды и процентных ставок. В ряде практических задач начальная (P) и конечная (S) суммы заданы контрактом, и требуется определить либо срок платежа, либо процентную ставку, которая в данном случае может служить мерой сравнения с рыночными показателями и характеристикой доходности операции для кредитора. Указанные величины нетрудно найти из исходных формул наращения или дисконтирования. По сути дела, в обоих случаях решается в известном смысле обратная задача. Срок ссуды. При разработке параметров соглашения и оценивании сроков достижения желательного результата требуется определить продолжительность операции (срока ссуды) четыре остальные параметры сделки: а) При наращивании по сложной годовой ставке i. Из исходной формулы наращения: следует, что: 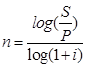 . (39) . (39)Причем логарифм можно взять по любому основанию, поскольку он имеется как в числителе, так и в знаменателе. б) При наращивании по номинальной ставке процентов m раз в году. Из формулы: 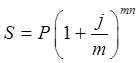 , ,получаем: 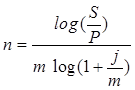 . (40) . (40)в) При дисконтировании по сложной годовой учетной ставке d. Из формулы: имеем: 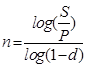 . (41) . (41)г) При дисконтировании по номинальной учетной ставке m раз в году. Из формулы: 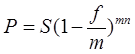 , ,приходим к формуле: 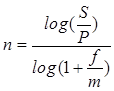 . (42) . (42)При наращивании по постоянной силе роста. Исходя из: получаем: 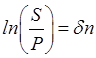 . (43) . (43)Расчет процентных ставок. Из тех же исходных формул, что и выше, получим выражения для процентных ставок: а) При наращивании по сложной годовой ставке i. Из исходной формулы наращения: следует, что: 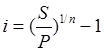 . (44) . (44)б) При наращивании по номинальной ставке процентов m раз в году из формулы: 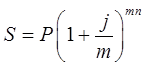 . .получаем: 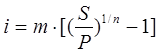 . (45) . (45)в) При дисконтировании по сложной годовой учетной ставке d. Из формулы: имеем: 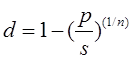 . (46) . (46)г) При дисконтировании по номинальной учетной ставке m раз в году. Из формулы: 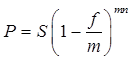 , ,приходим к формуле: 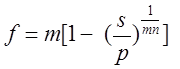 . (47) . (47)д) При наращивании по постоянной силе роста. Исходя из: получаем: 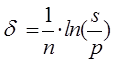 . (48) . (48)Пример 17. По вкладу 300000 руб. при 20 % годовых (проценты сложные) получена сумма 450000 руб. На какой срок был помещен депозит? Решение: 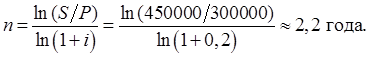 . .Пример 18. По вкладу 20000 руб. (проценты сложные) сроком на 3 года получена сумма 35000 руб. Какова процентная ставка? Решение: Пример 19. За какой срок сумма, равна 200000 рублей, достигнет 400000 рублей при начислении по сложной процентной ставке 19 % годовых? Рассмотреть случаи помесячного начисления процентов и один раз в году. Решение: m = 1. Тогда наращенная сумма равна: n= (ln(S/P))/( ln(1+ i)) = (ln(400000/200000))/( ln(1+0,19)) = 3,98 года. m=12 (в году 12 месяцев). Тогда наращенная сумма равна: n=(ln(S/P))/(m ln(1+ j∕m))= ln(400000/200000)/12 ln(1+0,19/12) =3,59 года. Пример 20. Финансовый инструмент куплен за 50000 рублей, его выкупная цена составила через 1,8 года 700000 рублей, проценты начисляются один раз в месяц. Определить доходность операции в виде номинальной ставки процентов. Решение: Находим номинальную ставку по формуле: Вопрос 5. Эквивалентность процентных ставок. Достаточно часто в практике возникает ситуация, когда необходимо произвести между собой сравнение по выгодности условий различных финансовых операций и коммерческих сделок. Условия финансово-коммерческих операций могут быть весьма разнообразными и напрямую несопоставимыми. Для сопоставления альтернативных вариантов ставки, используемые в условиях контрактов, приводят к одному показателю. Эквивалентными процентными ставками называют любые две из перечисленных выше ставок, которые при замене одна на другую приводят к одинаковым финансовым результатам, то есть отношения сторон не изменяются в рамках одной финансовой ситуации. Различные финансовые схемы можно считать эквивалентными в том случае, если они приводят к одному и тому же финансовому результату. Классическим примером эквивалентности являются номинальная и эффективная ставка процентов: 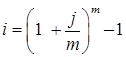 . (49) . (49)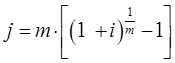 . (50) . (50)Эффективная ставка измеряет тот относительный доход, который может быть получен в целом за год, т.е. совершенно безразлично – применять ли ставку j при начислении процентов m раз в год или годовую ставку i, – и та, и другая ставки эквивалентны в финансовом отношении. Поэтому совершенно не имеет значения, какую из приведенных ставок указывать в финансовых условиях, поскольку использование их дает одну и ту же наращенную сумму. В США в практических расчетах применяют номинальную ставку, а в европейских странах предпочитают эффективную ставку процентов. Если две номинальные ставки определяют одну и ту же эффективную ставку процентов, то они называются эквивалентными. Эквивалентность простых процентных ставок (is,ds) определяется при одинаковых временных базах: 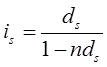 . (51) . (51)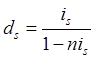 , (52) , (52)где is– ставка простых процентов; ds– простая учетная ставка; n– срок в годах. Эквивалентность простых (is, ds) и сложных (i, d) процентных ставок определяется соотношениями: · Эквивалентность isи i: 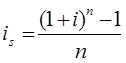 . (53) . (53)· Эквивалентность is и j: 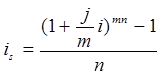 . (55) . (55)· Эквивалентность dsи i: 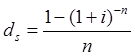 . (57) . (57)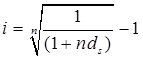 . (58) . (58)· Эквивалентность dsи j: 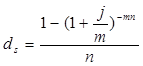 . (59) . (59)Эквивалентность сложных (i,j,d) процентных ставок определяется соотношениями: 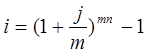 . (60) . (60)Эквивалентность сложных дискретных и непрерывных ставок: · эквивалентность i и δ: · эквивалентность δ и j: 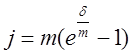 . (67) . (67)· эквивалентность δ и d: Пример 21. Каковы будут эквивалентные номинальные процентные ставки с полугодовым начислением процентов и ежемесячным начислением процентов, если соответствующая им эффективная ставка должна быть равна 25 %? Решение: Находим номинальную ставку для полугодового начисления процентов: 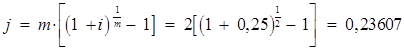 . .Находим номинальную ставку для ежемесячного начисления процентов: 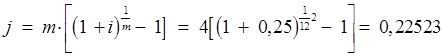 . .Таким образом, номинальные ставки 23,61 % с полугодовым начислением процентов и 22,52 % с ежемесячным начислением процентов являются эквивалентными. Пример 22. Предполагается поместить капитал на 4 года либо под сложную процентную ставку 20 % годовых с полугодовым начислением процентов, либо под простую процентную ставку 26 % годовых. Найти оптимальный вариант. Решение: Находим для сложной процентной ставки эквивалентную простую ставку: 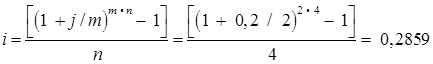 . .Таким образом, эквивалентная сложной ставке по первому варианту простая процентная ставка составляет 28,59 % годовых, что выше предлагаемой простой ставки в 26 % годовых по второму варианту, следовательно, выгоднее разместить капитал по первому варианту, т.е. под 20 % годовых с полугодовым начислением процентов. Находим эквивалентную сложную ставку процентов для простой ставки: Таким образом, процентная ставка 18,64 % годовых с полугодовым начислением процентов ниже 20 % годовых с полугодовым начислением процентов, то первый вариант выгоднее. Пример 23. Определить силу роста для сложной процентной ставке и наращение 20 % годовых. Решение: Вопрос 6. Начисление процентов и инфляция. Индекс покупательной способности. Индекс цен. Реально наращенная сумма. Темп инфляции. Инфляционная премия, Брутто-ставка. Формула Фишера. Начисление процентов и инфляция. Без учета инфляции конечные результаты расчетов денежных потоков являются весьма условными. Следствием инфляции является падение покупательной способности денег, которое за период n характеризуется индексом Jn. Индекс покупательной способности равен обратной величине индекса цен Jp, т.е.: 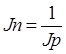 . (70) . (70)Индекс цен показывает во сколько раз выросли цены за указанный промежуток времени. Он может быть рассчитан по формуле Пааше, как отношение произведения цены товара в исследуемом и базисном периоде на его количество. Наращение по простым процентам. Если наращенная за n лет сумма денег составляет S, а индекс цен равен Jp, то реально наращенная сумма денег, с учетом их покупательной способности, равна: 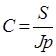 . (71) . (71)Пусть ожидаемый средний годовой темп инфляции (характеризующий прирост цен за год) равен h. Тогда годовой индекс цен составит (1+h). Если наращение производится по простой ставке в течение n лет, то реальное наращение при темпе инфляции h составит: 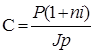 , (72) , (72)где в общем случае: и, в частности, при неизменном темпе роста цен h: Процентная ставка, которая при начислении простых процентов компенсирует инфляцию, равна: Один из способов компенсации обесценения денег заключается в увеличении ставки процентов на величину так называемой инфляционной премии. Скорректированная таким образом ставка называется брутто-ставкой. Брутто-ставка, которую мы будем обозначать символом r, находится из равенства, скорректированного на инфляцию множителя наращения по брутто-ставке множителю наращения по реальной ставке процента: 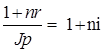 , (76) , (76)откуда: 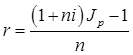 . (77) . (77)Пример 24. Каждый месяц цены растут на 1,5 %. Каков ожидаемый уровень инфляции за год? Решение: Замечание. Простой ответ 12 1,5 % = 18 % – не правильный. Цены растут на 1,5 % каждый месяц от достигнутого уровня, то есть рост идет по сложной процентной ставке. Тогда годовой индекс инфляции Пример 25. Уровень инфляции в марте составила 2 %, в апреле 1 %, в мае 3 %. Найти уровень инфляции за 3 месяца. Решение: Индекс цен за рассматриваемый период равен 𝐼𝑝=(1+0,02)∙(1+0,01)∙(1+0,03)≈1,061. Т.е. уровень инфляции за рассматриваемый период составил 6,1 %. Пример 26. Период начисления n = 3 месяца, ожидаемый ежемесячный уровень инфляции 2 %. Под какую простую ставку процентов нужно положить первоначальную сумму, чтобы обеспечить реальную доходность i = 5 % годовых (проценты простые)? Решение: Ожидаемый индекс инфляции за период начисления n = 3 месяца = 0,25 года, то есть уровень инфляции за рассматриваемый период. Тогда Наращение по сложным процентам. Наращенная по сложным процентам сумма к концу срока ссуды с учетом падения покупательной способности денег (т.е. в неизменных рублях) составит: 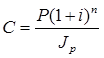 , (78) , (78)где индекс цен определяется выражением (74) или (75), в зависимости от непостоянства или постоянства темпа инфляции. В этом случае падение покупательной способности денег компенсируется при ставке i = h, обеспечивающей равенство C = P. Применяются два способа компенсации потерь от снижения покупательной способности денег при начислении сложных процентов: а) Корректировка ставки процентов, по которой производится наращение, на величину инфляционной премии. Ставка процентов, увеличенная на величину инфляционной премии, называется брутто-ставкой. Будем обозначать ее символом r. Считая, что годовой темп инфляции равен h, можем написать равенство соответствующих множителей наращения: где i– реальная ставка. б) Отсюда получаем формулу Фишера: r=i+h+ih, (80) то есть инфляционная премия равна h+ih. в) Индексация первоначальной суммы P. В этом случае сумма P корректируется согласно движению заранее оговоренного индекса. Тогда: Нетрудно заметить, что и в случае А) и в случае Б) в итоге мы приходим к одной и той же формуле наращения (81). В ней первые два сомножителя в правой части отражают индексацию первоначальной суммы, а последние два – корректировку ставки процента. Измерение реальной ставки процента. На практике приходится решать и обратную задачу – находить реальную ставку процента в условиях инфляции. Из тех же соотношений между множителями наращения нетрудно вывести формулы, определяющие реальную ставку i по заданной (или объявленной) брутто-ставке r. При начислении простых процентов годовая реальная ставка процентов равна 1+nr. 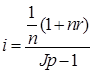 . (82) . (82)При начислении сложных процентов реальная ставка процентов определяется следующим выражением: 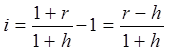 . (83) . (83)Пример 27. Какую ставку должен назначить банк, если темп годовой инфляции составил 12 %, а реальная ставка оказалась 6 %? Решение: Требуемая номинальная ставка равна по формуле (50): Пример 28. На сумму 1,5 млн руб. в течение трех месяцев начисляются простые проценты из расчета 28 % годовых. Ежемесячная инфляция в рассматриваемом периоде характеризуется темпами 2, 5, 2 %. Определить наращенную сумму с учетом инфляции. Решение: Индекс цен в рассматриваемом периоде равен: Наращенная сумма с учетом инфляции: 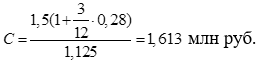 Пример 29. При двух одинаковых процентных повышениях заработная плата с 10 тыс. руб. в год обратилась в 12544 руб. Определите, на сколько процентов повышалась она каждый раз? Решение: откуда: 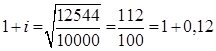 , ,и поэтому: i = 12 %. Пример 30. Через сколько лет начальная сумма депозита возрастет в 2 раза при начислении 9,75 % годовых? Рассчитать в двух случаях: а) простые проценты; б) сложные проценты с полугодовой капитализацией. Решение: а) простые проценты: 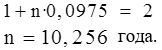 б) сложные проценты с полугодовой капитализацией: Пример 31. Период начисления n = 3 года, ожидаемый ежегодный уровень (темп) инфляции 14 %. Под какую сложную ставку ссудных процентов нужно положить первоначальную сумму, чтобы обеспечить реальную доходность i = 5 % годовых (проценты сложные)? Решение: Ожидаемый индекс цен за период начисления  Вывод: Реальную доходность в 5% годовых с учетом инфляции обеспечит реальная ставка 19,8%. Пример 32. Первоначальная сумма положена на n = 3 года под сложную ставку ссудных процентов годовых. Уровень инфляции за 1-й год составил 16 %, за 2-й год – 14 %, за 3-й год – 13 %. Какова реальная доходность в виде сложной годовой ставки ссудных процентов? Решение: Индекс цен за рассматриваемый период n = 3 года тогда уровень инфляции Hp за рассматриваемый период Hp=0,494. Реальная доходность в виде годовой сложной ставки ссудных процентов Замечание. Аналогично можно найти процентную ставку, учитывающую инфляцию, и для других процентных и учетных ставок. |
