Финансовая математика. Тема Простые проценты
 Скачать 0.99 Mb. Скачать 0.99 Mb.
|
|
Тема 4. Анализ кредитных операций ило торговца. Переменная сумма счета и расчет процентов. Изменение условий контракта. Финансовая или кредитная операции предполагают сбалансированность вложений и отдачи. Понятие сбалансированности можно пояснить на графике. Пусть ссуда в размере D0 выдана на срок T. На протяжении этого срока в счет погашения задолженности производятся, допустим, два промежуточных платежа R1 и R2, а в конце срока выплачивается остаток задолженности R3, подводящий баланс операции. На интервале времени t1 задолженность возрастает до величины D1. В момент t1 долг уменьшается до величины K1=D1-R1 и т.д. 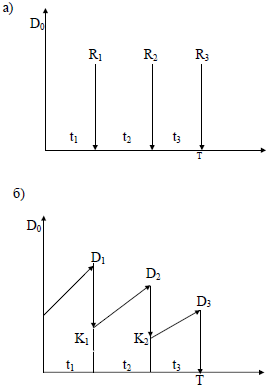 Рис. 1. Контур финансовой операции Заканчивается операция получением кредитором остатка задолженности R3. В этот момент задолженность полностью погашается. Назовем график (рис. 1) типа б) контуром финансовой операции. Сбалансированная операция обязательно имеет замкнутый контур, т.е. последняя выплата полностью покрывает остаток задолженности. Контур операции обычно применяется при погашении задолженности частичными промежуточными платежами. Формула погашения задолженности равными частями имеет вид: 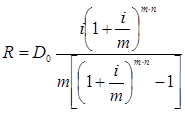 . (113) . (113)С помощью последовательных частичных платежей иногда погашаются краткосрочные обязательства. В этом случае существуют два метода расчета процентов и определения остатка задолженности. Первый называется актуарным и применяется в основном в операциях со сроком более года. Второй метод назван правилом торговца. Он обычно применяется коммерческими фирмами в сделках со сроком не более года. При начислении процентов, как правило, используются обыкновенные проценты с приближенным числом дней временных периодов. Актуарный метод. Актуарный метод предполагает последовательное начисление процентов на фактические суммы долга. Частичный платеж идет в первую очередь на погашение процентов, начисленных на дату платежа. Если величина платежа превышает сумму начисленных процентов, то разница идет на погашение основной суммы долга. Непогашенный остаток долга служит базой для начисления процентов за следующий период и т.д. Если же частичный платеж меньше начисленных процентов, то никакие зачеты в сумме долга не делаются. Такое поступление приплюсовывается к следующему платежу. Сбалансированная операция имеет замкнутый контур, то есть последняя выплата полностью покрывает остаток задолженности. Для случая, показанного на рисунке, получим следующие расчетные формулы для определения остатка задолженности: где t1, t2, t3– периоды времени заданы в годах; i – процентная годовая ставка. Правило торговца. Правило торговца является другим подходом к расчету частичных платежей. Здесь возможны две ситуации: 1. Если срок ссуды не превышает одного года, то сумма долга с начисленными за весь срок процентами остается неизменной до полного погашения. Одновременно идет накопление частичных платежей в погасительном фонде с начисленными на них до конца срока процентами, сумма которых после наращения к концу срока должна быть равна наращенной сумме долга. Погасительный фонд создается из последовательных взносов должника (например, специальный накопительный счет в банке), на которые начисляются проценты. Взносы могут быть как постоянными, так и переменными во времени. При создании погасительного фонда используют две процентные ставки: r и a. Первая определяет темп роста погасительного фонда, а вторая – сумму выплачиваемых за долг процентов. Понятно, что создание фонда выгодно только тогда, когда r > a, так как должник на аккумулируемые в погасительном фонде средства получает больше процентов, чем сам выплачивает за заем. Чем больше разность r – a, тем больше экономия средств должника, направляемая на покрытие долга. В случае r = a преимущества создания погасительного фонда пропадают. 2. В случае, когда срок превышает год, указанные выше расчеты, делаются для годового периода задолженности. В конце года из суммы задолженности вычитается наращенная сумма накопленных частичных платежей. Остаток погашается в следующем году. При общем сроке ссуды T≤1 алгоритм можно записать следующим образом: где S– остаток долга на конец срока; D – наращенная сумма долга; K – наращенная сумма платежей; Rj – сумма частичного платежа; tj– интервал времени от момента платежа до конца срока; m – число частичных (промежуточных) платежей. Пример 1. Ссуда в размере 100000 рублей выдана 1 февраля по 1 августа включительно под простые проценты 18 % годовых. В счет погашения долга 16 апреля поступило 60 тысяч рублей, а 16 июня – 100 рублей. Определить остаток долга на конец срока актуарным методом и правилом торговца. Решение: а) актуарный метод; При расчете определим промежутки времени: 1 февраля – 16 апреля – 75 дней. 16 апреля – 16 июня – 60 дней. 16 июня – 1 августа – 45 дней. На 16 апреля до частичной выплаты величина долга составит: После частичной выплаты: На 16 июня до частичной выплаты величина долга составит: Так как проценты в данном случае Больше взноса, равного 100 рублей, то взнос не засчитывается и переносится на следующий платеж. На 1 августа наращенная величина долга составит: Окончательный платеж 1 августа будет равен: б) правило торговца; При расчете потребуются следующие промежутки времени: 1 февраля – 1 августа – 180 дней; 16 апреля – 1 августа – 105 дней; 16 июня – 1 августа – 45 дней. Подставив полученные данные в формулу (111), получим: Таким образом, последняя выплата, рассчитанная актуарным методом, больше на 21,94 рубля последнюю выплату, рассчитанную при помощи правила торговца. Переменная сумма счета и расчет процентов. Рассмотрим ситуацию, когда в банке открыт сберегательный счет, и сумма счета в течение срока хранения изменяется: денежные средства снимаются, делаются дополнительные взносы. Тогда в банковской практике при расчете процентов часто используют методику расчета с вычислением так называемых процентных чисел. Каждый раз, когда сумма на счете изменяется, вычисляется процентное число Cj за прошедший период j, в течение которого сумма на счете оставалась неизменной, по формуле: 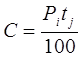 , ,где tj – длительность j-того периода в днях. Для определения суммы процентов, начисленной за весь срок, все процентные числа складываются, и их сумма делится на постоянный делитель D: где K – временная база (число дней в году, т.е. 360, либо 365, либо 366); i–годовая ставка простых процентов. При закрытии счета владелец получит сумму равную последнему значению суммы на счете плюс сумму процентов. Пример 2. Пусть 20 февраля был открыт счет до востребования в размере P1=3000 руб., процентная ставка по вкладу равнялась 20 % годовых. Дополнительный взнос на счет составил R1=2000 руб. и был сделан 15 августа. Снятие со счета в размере R2=-4000 руб. зафиксировано 1октября, а 21 ноября счет был закрыт. Требуется определить сумму процентов и общую сумму, полученную вкладчиком при закрытии счета. Решение: Расчет будем вести по схеме (360/360). Здесь имеются три периода, в течение которых сумма на счете оставалась неизменной: с 20 февраля по 15 августа: P1=3000, t1=10+5·30+15=175, с 15 августа по 1 октября: P2=P1+R1=3000+2000=5000 руб., t2=15+30+1=46, с 1 октября по 21 ноября: P3=P2+R2=5000-4000=1000 руб., t3=29+21=50. Найдем процентные числа: Постоянный делитель Сумма процентов равна: Сумма, выплачиваемая при закрытии счета, равна P3+I=1000+447.22=1447 руб. 22 коп. Теперь покажем связь этой методики с формулой простых процентов. Рассмотрим в алгебраическом виде представленный выше пример. Сумму, выплачиваемую при закрытии счета, найдем следующим образом: 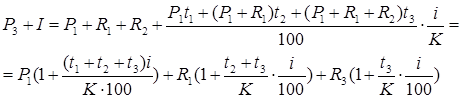 . .Таким образом, мы получили выражение, из которого следует, что на каждую сумму, добавляемую или снимаемую со счета, начисляются проценты с момента совершения соответствующей операции до закрытия счета. Эта схема соответствует правилу торговца. Изменение условий контракта. В практике часто возникает необходимость в изменении условий контракта: например, должник может попросить об отсрочке срока погашения долга или, напротив, изъявить желание погасить его досрочно, в ряде случаев может возникнуть потребность объединить (консолидировать) несколько долговых обязательств в одно и т.д. Во всех этих случаях применяется принцип финансовой эквивалентности старых (заменяемых) и новых (заменяющих) обязательств. Для решения задач по изменению условий контракта разрабатывается уравнение эквивалентности, в котором сумма заменяемых платежей, приведенных к какому-либо одному моменту времени, приравнивается сумме платежей по новому обязательству, приведенных к той же дате. Для краткосрочных контрактов применяются простые процентные ставки, а для средне- и долгосрочных - сложные ставки. Вопрос 2. Варианты погашения долга и составление плана погашения кредита. Ипотека. Виды кредитов. Варианты погашения долга и составление плана погашения кредита. Основная сумма долга может быть погашена целиком по окончании срока кредита или может погашаться постепенно в течение всего срока. Проценты обычно выплачивают от суммы непогашенного остатка кредита (от остаточной суммы долга). Существуют различные варианты порядка погашения основной суммы долга: 1. единовременное погашение основного долга и процентов; 2. погашение периодическими взносами: а) с равномерным погашением основной суммы долга (дифференцированный платеж); б) с неравномерным погашением основной суммы долга. 3. амортизационное – постепенная выплата равномерными погасительными взносами основной суммы долга и процентов – аннуитетный платеж. В практической финансовой деятельности долг обычно погашается в рассрочку, частями. Такой метод называется амортизацией долга. Он может погашаться равными или переменными суммами: Рассмотрим задачу погашения долга в виде плана создания погасительного фонда, который заключается в определении размера постоянных срочных уплат (аннуитетов) и составляющих их элементов, зависящих от конкретных условий договора займа. Пусть накопление производится путем регулярных ежегодных взносов R, на которые начисляют сложные проценты по ставке r. Одновременно происходит выплата процентов за долг по ставке a. Тогда срочная уплата составит: Y=Aa+R. (116) Пусть фонд должен быть составлен за N лет. Тогда соответствующие взносы образуют постоянную ренту с параметрами: R, N, r. Пусть взносы и проценты выплачиваются в конце года (обычная рента постнумерандо). Тогда: Тогда срочна уплата находится так: Если проценты присоединяются к основному долгу и выплачиваются в конце срока, то срочная уплата равна: 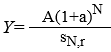 . (119) . (119)Пример 3. Долг в сумме 1 млн руб., выданный под 12 % годовых, выплачивается равными суммами в течение четырех лет в конце каждого года. Для этого создается погасительный фонд, в котором на инвестированные средства начисляются проценты по ставке 15 %. Определить размеры срочных уплат при ежегодной выплате процентов и при выплате процентов в конце срока. Решение: Таким образом имеем: А=1млн, n=N=4, a=12%, r =15%. Находим S4;15= 4,9933 и, следовательно, Y=1000 000·0,12+ 1000 000/4,9933 = 320268,3596. При выплате процентов в конце срока срочные уплаты равны: 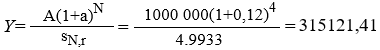 . .Рассмотрим задачу погашения основного долга равными суммами (дифференцированный метод). Пусть долг в сумме А погашается в течение n лет. Тогда сумма погасительного платежа cоставит . При погашении долга равными суммами в конце каждого года в течение n лет величина долга будет убывать на сумму . После очередной выплаты величина долга в конце года под номером j будет равна: Срочная уплата, состоящая из ежегодной выплаты основного долга и и процентов Aj-1 a в году под номером j , будет равна: Пример 4. (Дифференцированный метод). Сумму долга необходимо погасить в течение четырех лет равными суммами. Выплаты основного долга производятся и проценты на долг по ставке 12 % годовых начисляются в конце каждого года. Составить план погашения долга. |
