Финансовая математика. Тема Простые проценты
 Скачать 0.99 Mb. Скачать 0.99 Mb.
|
|
Решение: Срочные уплаты находят по формуле (120): 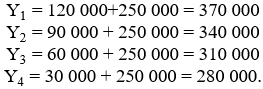 Полученные результаты удобно свести в таблицу.
Рассмотрим задачу погашения долга равными срочными уплатами. В соответствии с этим методом расходы должника по обслуживанию долга постоянны на протяжении всего срока его погашения. Из общей суммы ежегодной выплаты часть выделяется на уплату процентов, остаток идет на погашение основного долга. По определению: где j– номер года 1,2,3,…n; Aj-1 - остаток долга в конце года под номером j-1; Rj -сумма выплаты основного долга в конце года под номером j. Величину срочной уплаты можно определить как годовую выплату обычной ренты с процентной ставкой а, срокомn и современной стоимостью, равной величине долга А: где ana коэффициент приведения обычной годовой ренты постнумерандо со ставкой а и сроком n. Найдем сумму первого погасительного платежа. По определению: Остаток основного долга в конце года под номером j после выплат вычисляют по формулам: Из (6) следует: Из соотношения (124) следует: Тогда: Из (122): Подставим в (127): Пример 5. Ссуду долга в 1 млн рублей необходимо погасить в течение четырех лет равными срочными уплатами. Срочные уплаты производятся в конце каждого года. Проценты начисляют по ставке 12 % годовых. Составить план погашения долга. Решение: Ежегодные срочные уплаты образуют обычную ренту с параметрами: n = 4, i = 12 %, A = 1 млн руб., где коэффициент наращения = 3,037. Тогда: Значение выплаты в конце первого года определяют по формуле: Проценты в конце первого года равны: Выплаты основного долга каждого года определяются по формуле (128).  Ежегодные выплаты процентов определяются соотношением: Проведя расчеты по этой формуле, получим ежегодные выплаты процентов для второго, третьего и четвертого годов:  Остаток основного долга в конце каждого года после выплат вычисляют по формуле (124). Полученные результаты сведем в таблицу:
Сопоставим размеры процентов по двум вариантам погашения кредита. При равномерном погашении основной суммы долга проценты составили 300 000 рублей. Погашение долга равными срочными уплатами приводит к сумме процентов 316 937,76 рублей. С точки зрения заемщика более выгоден вариант равномерного погашения основного долга. Для банка погашение долга равными срочными уплатами привлекательно большей суммой процентных выплат, хотя, с другой стороны, остается большая сумма непогашенного долга, что означает больший кредитный риск для банка. Следует учесть также и минимизацию операционных издержек, и контроль за погашением долга. В этой связи вариант погашения равными срочными уплатами получил широкое распространение в ипотечном и потребительском кредите. Пример 6. Ссуду долга в 1 млн рублей необходимо погасить в течение четырех лет равными срочными уплатами. Срочные уплаты производятся в конце каждого года. Проценты начисляют по ставке 12 % годовых. Составить план погашения долга. Решение: Ежегодные срочные уплаты образуют обычную ренту с параметрами: n=4, i= 12%, A=1 млн руб., где коэффициент наращения a4.12 = 3,037. Тогда: Значение выплаты в конце первого года определяют по формуле: Проценты в конце первого года равны: Выплаты основного долга каждого года определяются по формуле (128).  . .Ежегодные выплаты процентов определяются соотношением: Проведя расчеты по этой формуле, получим ежегодные выплаты процентов для второго, третьего и четвертого годов: 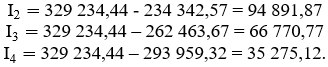 Остаток основного долга в конце каждого года после выплат вычисляют по формуле (125). Полученные результаты сведем в таблицу:
Сопоставим размеры процентов по двум вариантам погашения кредита. При равномерном погашении основной суммы долга проценты составили 300 000 рублей. Погашение долга равными срочными уплатами приводит к сумме процентов 316 937,76 рублей. С точки зрения заемщика более выгоден вариант равномерного погашения основного долга. Для банка погашение долга равными срочными уплатами привлекательно большей суммой процентных выплат, хотя, с другой стороны, остается большая сумма непогашенного долга, что означает больший кредитный риск для банка. Следует учесть также и минимизацию операционных издержек, и контроль за погашением долга. В этой связи вариант погашения равными срочными уплатами получил широкое распространение в ипотечном и потребительском кредите. Ипотека. Одним из социально-значимых видов кредитной операции является ипотека. Ипотечные ссуды выдаются коммерческими банками и специальными ипотечными банками, ссудно-сберегательными ассоциациями. Характерной особенностью ипотечных ссуд является длительный срок погашения. В среднем срок ипотеки составляет 10-15 лет, а максимальный срок ипотеки - 50 лет. Поскольку платежи по обслуживанию долга, то есть по уплате процентов и погашению предоставленного кредита, являются регулярными, то и расчет ипотеки сводится к расчету параметров того или иного вида ренты. Основной задачей расчета является разработка планов погашения и остатка задолженности на любой момент времени. Существует несколько видов ипотечных ссуд, различающихся в основном методами погашения задолженности. У ипотеки есть два вида погашения: аннуитетный (одинаковый от начала и до конца – стандартная ипотека) и дифференцированный. При дифференцированных платежах сумма основного долга выплачивается равными ежемесячными долями, а проценты по кредиту рассчитываются на остаток невыплаченной суммы. Таким образом, с каждым разом размер суммы платежа становится меньше. Сумма выплат при аннуитетном способе погашения больше, чем сумма выплат при дифференцированном погашении. Поэтому банки в основном выдают ипотеку в виде аннуитетных платежей. Более наглядным и эффективным способом планирования долга является составление таблиц, в которых отражают все основные характеристики обслуживания долга. Покажем это на примере: Пример 7. (Дифференцированный способ погашения). Кредит в сумме 100 тыс. руб. требуется погасить за 5 лет равными суммами в конце каждого года. На непогашенный остаток суммы кредита начисляются ежегодные проценты в размере 10 %. Составить план погашения долга. Решение: План погашения долга приведем в таблице с расчетами:
Со временем уменьшаются размер платежа и сумма процентов. Пример 8. (Аннуитетные платежи). Рассмотрим предыдущий пример, изменив условия: выплату кредита осуществить равными долями. Решение: 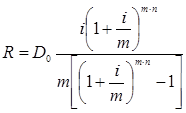 . (129) . (129)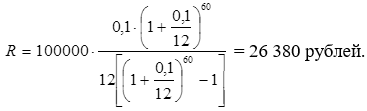 Вывод: Выплаты аннуитетными платежами составляют большую сумму, чем при дифференцированном способе погашения. Рассмотрим случай выплат процентов по долгу в конце каждого года поcтонными суммами по i. Расходы, состоящие из процентов по долгу I и ежегодных выплат в фонд R есть срочная уплата Y. Если проценты выплачиваются ежегодно, тогда величина срочной уплаты (расходов должника по погашению долга) равна: 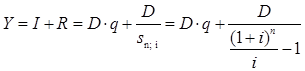 , (130) , (130)где Y– срочная уплата; R- ежегодная выплата; I – выплата процентов по долгу; D– первоначальная сумма долга; q– ставка процентов по условиям займа; sn; i– коэффициент наращения финансовой ренты; n – срок долга в годах; i – ставка процентов при создании фонда погашения. Здесь фигурируют две ставки процентов: i – определяет скорость роста суммы фонда погашения; q– сумму выплачиваемых за заем процентов. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
