Финансовая математика. Тема Простые проценты
 Скачать 0.99 Mb. Скачать 0.99 Mb.
|
|
Пример 9. Долг 100 тыс. рублей выдан под 10 % годовых на 3 года, с ежегодной выплатой процентов по долгу. Для погашения суммы долга единовременным платежом создается фонд, куда ежегодно вносятся равные суммы, на которые начисляются проценты по ставке 11 %. Найти ежегодные расходы должника. Решение: Ежегодные расходы должника составляют величину срочной уплаты: 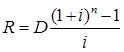 . (131) . (131)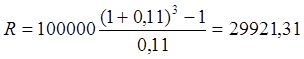 , ,отсюда: Таким образом, ежегодные расходы должника по обслуживанию долга составят 39 921,31 рублей. Однако более наглядным и эффективным способом планирования долга является составление таблиц, в которых отражают все основные характеристики обслуживания долга. Покажем это на примере: Пример 10. Долг 100 тыс. рублей выдан под 10 % годовых на 3 года, с ежегодной выплатой процентов по долгу, как суммы основного долга, так и выплаты процентов. Для погашения суммы долга единовременным платежом создается фонд, куда ежегодно вносятся равные суммы, на которые начисляются проценты по ставке 11 %. Найти ежегодные расходы должника. Решение: Величина срочной уплаты равна: 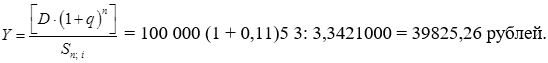 Таким образом, величина ежегодных расходов по обслуживанию долга оставит 39825,26 долларов, что несколько меньше аналогичного показателя в предыдущем примере, следовательно, меньше и общая сумма расходов по обслуживанию долга, составляющая величину 119475,78 рублей. Для более наглядного представления плана погашения долга здесь также необходимо составление таблицы. План погашения долга единовременным платежом
Как видно из таблицы, происходит ежегодное увеличение суммы долга за счет присоединения к нему процентов, поэтому к концу срока долг возрастет до 133100 рублей, из которых выплата процентов составит 33100 рублей. Однако за счет увеличения размера взносов в погасительный фонд общая величина обслуживания долга уменьшается. Пример 11. Сумма 100 тыс. долларов выдана под 10 % годовых на 3 года. Определить величину срочной уплаты при погашении основной суммы долга равными ежегодными частями. Решение: Величина суммы погашения долга равна: Поскольку величина срочной уплаты при таком способе погашения долга меняется из года в год, то и в этом случае строим план погашения долга в виде таблицы. План погашения основной суммы долга равными частями
Таким образом, общие расходы по обслуживанию долга составили 120 тыс. долларов, из которых 20 тыс. долларов составляют проценты, а 100 тыс. долларов – погашение основной суммы долга. Пример 12. Условия предыдущей задачи, но погашение долга предусматривает уплату равными срочными выплатами. Решение: Срочная уплата, включающая в себя погашение основной суммы долга и выплату процентов по долгу, равна: Отсюда общие расходы по погашению долга равны: Таким образом, ежегодные расходы по погашению долга будут составлять 40211,48 долларов, а за весь срок финансовой операции – 120634,44 доллара. При этом варианте погашенучетные ставкиия долга также можно построить таблицу. План погашения долга равными срочными уплатами
Таким образом, общие расходы по обслуживанию долга составляют 120634,44 долларов, из которых 100 тыс. долларов идут на погашение долга, а 20634,44 долларов – проценты. В таблице наглядно представлено распределение суммы срочной уплаты на выплату процентов и непосредственное погашение долга. Пример 13. Потребительский кредит на сумму 5 тыс. руб. открыт на 2 года по ставке 25 % годовых. Погашение кредита равными взносами ежеквартально. Определить стоимость кредита и размер ежеквартальных взносов. Решение: Стоимость кредита – это проценты, которые равны: Общая сумма расходов по обслуживанию кредита равна: Ежеквартальные взносы составят величину: Таким образом, ежеквартальные взносы в размере 937,50 рублей позволяет выплатить сумму долга и выплатить проценты. Виды кредитов. Доходность ссудных и учетных операций, предполагающих удержание комиссионных. Ссудные операции. За открытие кредита, учет векселей и другие операции кредитор часто взимает комиссионные, которые повышают доходность операций, так как размер фактически выданной ссуды сокращается. Пусть ссуда в размере D выдана на срок n, и при ее выдаче из нее удерживаются комиссионные в размере G. Фактически выданная ссуда равна D-G. Рассмотрим сначала сделки с начислением простых процентов по ставке i. Обозначим через iэ,пр – фактическую доходность, выраженную через ставку простых процентов, и пусть g – относительная величина комиссионных в сумме кредита, то есть G=Dg. Тогда из балансового уравнения: Находим: 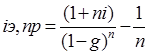 . (132) . (132)Теперь рассмотрим долгосрочную операцию, когда ссуда с удержанием комиссионных выдается под сложные проценты. Тогда балансовое уравнение имеет вид: откуда: 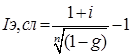 . (133) . (133)Пример 14. Ссуда 1 млн руб. выдана на 240 дней (К=360) под простые годовые проценты 12 %. При выдаче ссуды удерживают комиссионные в размере 10 тыс. руб. Определить полную доходность финансовой операции. Решение: Полная доходность финансовой операции вычисляется по формуле: 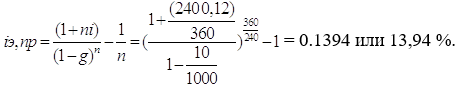 Учетные операции. Рассмотрим полную доходность банка при осуществлении операции учета с удержанием комиссионных. Пусть при учете применяется простая учетная ставка. После удержания комиссионных и дисконта заемщик получает сумму: G=Dg, то эта сумма составит D(1-nd-g). Балансовое уравнение принимает вид: откуда полная доходность: 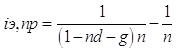 . (134) . (134)Форфейтная кредитная операция. Эта операция получила распространение во внешней торговле, но может применяться и во внутренней торговле страны. Потребность в такой операции возникает, когда покупатель приобретает товар, не имея соответствующих денежных средств, а продавец также не может продать товар в кредит. Тогда в рамках форфейтной операции покупатель выписывает комплект векселей на сумму, равную стоимости товара плюс проценты за кредит, который формально предоставляется покупателю продавцом. Сроки векселей равномерно распределены во времени обычно через равные интервалы (полугодия). Продавец сразу же после получения портфеля векселей учитывает его в банке без права оборота на себя, получая полностью деньги за свой товар. Банк, форфетируя сделку, берет весь риск на себя. Иногда в качестве четвертого агента сделки может выступать банк покупателя, гарантирующий погашение задолженности по векселям. Поскольку платежи по векселям представляют собой постоянную ренту, то и расчет таких операций опирается на уже полученные нами результаты. Ссуды с ростом платежей. В этом случае предусматривается постоянный рост расходов по обслуживанию долга в первые 5-10 лет. Затем погашение производится постоянными взносами. Расчет сводится к применению формул для рент с переменными и постоянными платежами в соответствующие интервалы времени. Ссуды с периодическим увеличением взносов. По согласованному графику каждые 3-5 лет сумма взносов увеличивается. Таким образом, поток платежей представляет собой последовательность постоянных рент. Ссуда с льготным периодом. В такой ипотеке предполагается наличие льготного периода, в течение которого выплачиваются только проценты по долгу. Ссуда с залоговым счетом. В этой схеме предполагается, что клиент в начале операции вносит на специальный (залоговый) счет некоторую сумму денег. На начальных этапах он выплачивает кредитору погасительные взносы, которые меньше тех, что необходимы по стандартной ипотеке. Недостающие суммы добавляются путем списания с залогового счета, пока он не иссякнет. Таким образом кредитор все время получает постоянные взносы, как и в стандартной ипотеке. А взносы должника характеризуются ростом во времени. Ссуды с периодическим изменением процентной ставки. Эта схема предполагает, что стороны каждые 3-5 лет пересматривают уровень процентной ставки с целью адаптации к условиям рынка. Ссуда с переменной процентной ставкой. Здесь уровень ставки привязывается к какому-либо распространенному финансовому показателю или индексу. Пересмотр обычно осуществляется по полугодиям. Чтобы избежать чрезмерных скачков, предусматривается верхняя и нижняя границы разовых корректировок (например, не более 2 %). Ипотека с обратным аннуитетом. Предназначена для заклада домов пожилыми владельцами (продажа в рассрочку с правом дожития). Цель такого залога – получение систематического дохода владельцем жилища. Льготные займы и кредит. В ряде случаев долгосрочные займы и кредиты выдаются на льготных для заемщика условиях. Низкая процентная ставка по сравнению с рыночной в сочетании с большим сроком и наличием льготного периода дают должнику существенную выгоду, которую можно рассматривать как субсидию. Такая субсидия оказывается как на международном уровне в рамках финансовой помощи развивающимся странам, так и внутри страны для поддержки отдельных отраслей или производств. Проблема определения размера этой помощи сводится к оценке грант-элемента. Грант-элемент – это условная субсидия кредитора, связанная с применением более низкой процентной ставки. Грант-элемент определяется в двух видах: в виде абсолютной и относительной величины. Абсолютный грант-элемент рассчитывается как разность суммы займа и современной величины платежей по погашению займа. Проблема здесь состоит в выборе ставки процентов для расчета современной величины платежей. Обычно используют ставку, применяемую на рынке долгосрочных кредитов. Абсолютный грант-элемент находится как: А относительный грант-элемент как: где W– абсолютный грант-элемент; w – относительный грант-элемент; D – сумма кредита; G – современная величина платежей, рассчитанная по реальной ставке рынка кредитов. Вопрос 3. Начисление простых и сложных процентов для операций с двойной конвертацией валюты. Зависимость доходности операций с двойной конвертацией от темпов роста обменного курса. Конвертация валюты и начисление простых процентов. Рассмотрим совмещение конвертации (обмена) валюты и наращение простых процентов, сравним результаты от непосредственного размещения имеющихся денежных средств в депозиты или после предварительного обмена на другую валюту. Всего возможно 4 варианта наращения процентов: 1. Без конвертации. Валютные средства размещаются в качестве валютного депозита, наращение первоначальной суммы производится по валютной ставке путем прямого применения формулы простых процентов. 2. С конвертацией. Исходные валютные средства конвертируются в рубли, наращение идет по рублевой ставке, в конце операции рублевая сумма конвертируется обратно в исходную валюту. 3. Без конвертации. Рублевая сумма размещается в виде рублевого депозита, на который начисляются проценты по рублевой ставке по формуле простых процентов. 4. С конвертацией. Рублевая сумма конвертируется в какую-либо конкретную валюту, которая инвестируется в валютный депозит. Проценты начисляются по валютной ставке. Наращенная сумма в конце операции обратно конвертируется в рубли. Операции без конвертации не представляют сложности. В операции наращения с двойной конвертацией имеются два источника дохода: начисление процента и изменение курса. Причем начисление процента является безусловным источником (ставка фиксирована, инфляцию пока не рассматриваем). Изменение же обменного курса может быть как в ту, так и в другую сторону, и оно может быть как источником дополнительного дохода, так и приводить к потерям. Далее мы конкретно остановимся на двух вариантах (2 и 4), предусматривающих двойную конвертацию. Предварительно введем следующие обозначения: · Pv– сумма депозита в валюте; · Pr– сумма депозита в рублях; · Sv – наращенная сумма в валюте; · Sr – наращенная сумма в рублях; · K0– курс обмена в начале операции (курс валюты в руб.); · K1– курс обмена в конце операции; · n – срок депозита; · i – ставка наращения для рублевых сумм (в виде десятичной дроби); · j– ставка наращения для конкретной валюты. Вариант: валюта→ рубли → рубли → валюта. Операция состоит из трех этапов: обмена валюты на рубли, наращения рублевой суммы, обратное конвертирование рублевой суммы в исходную валюту. Наращенная сумма, получаемая в конце операции в валюте, составит: 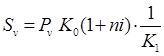 . (137) . (137)Как видим, три этапа операции нашли свое отражение в этой формуле в виде трех сомножителей. Множитель наращения с учетом двойной конвертации равен: 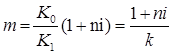 , (138) , (138)где Множитель наращения m связан линейной зависимостью со ставкой i и обратной с обменным курсом в конце операции K1 (или с темпом роста обменного курса k). Исследуем теоретически зависимость общей доходности операции с двойной конвертацией по схеме: Валюта → рубли → рубли →валюта. от соотношения конечного и начального курсов обмена k. Простая годовая ставка процентов, характеризующая доходность операции в целом, равна: 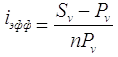 . (139) . (139)Подставим в эту формулу записанное ранее выражение для Sv: 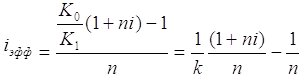 . (140) . (140)Таким образом с увеличением k доходность iэфф падает по гиперболе с асимптотой –1/n: (см. рис. 2). 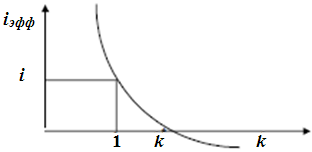 Рис. 2. Исследуем особые точки этой кривой. Отметим, что при k=1 доходность операции равна рублевой ставке, т.е. iэфф=i. При k>1 iэфф Из равенства iэфф = 0 находим, что k* = 1+ni, что в свою очередь означает: Вывод 1: Если ожидаемые величины k или K1 превышают свои критические значения, то операция явно убыточна (iэфф<0). Теперь определим максимально допустимое значение курса обмена в конце операции K1, при котором эффективность будет равна существующей ставке по депозитам в валюте, и применение двойной конвертации не дает никакой дополнительной выгоды. Для этого приравняем множители наращения для двух альтернативных операций: 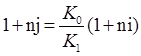 . (142) . (142)Из записанного равенства следует, что: 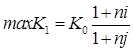 , (142), , (142),или 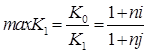 . (143) . (143)Вывод 2: Депозит валюты через конвертацию в рубли выгоднее валютного депозита, если обменный курс в конце операции ожидается меньше max K1. Вариант: рубли → валюта → валюта → рубли. Рассмотрим теперь вариант с двойной конвертацией, когда имеется исходная сумма в рублях. В этом случае трем этапам операции соответствуют три сомножителя следующего выражения для наращенной суммы: 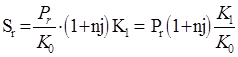 . (144) . (144)Здесь также множитель наращения линейно зависит от ставки, но теперь от валютной ставки процентов. От конечного курса обмена он также зависит линейно. Проведем теоретический анализ эффективности этой операции с двойной конвертацией и определим критические точки. Доходность операции в целом определяется по формуле: 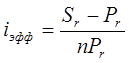 . .Отсюда, подставив выражение для Sr, получаем: 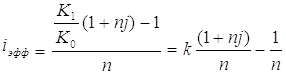 . (145) . (145)Зависимость показателя эффективности iэфф от k линейная, она представлена на рис. 3: 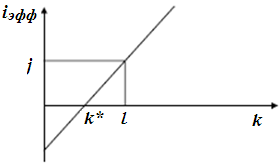 Рис. 3. При k=1 iэфф=j, при k>1 iэфф>j, при k<1 iэфф<j. Найдем теперь критическое значение k*, при котором iэфф=0. Оно оказывается равным: 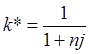 , (146) , (146)или 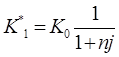 . (147) . (147)Вывод 3: Если ожидаемые величины k или K1 меньше своих критических значений, то операция явно убыточна (iэфф<0). Минимально допустимая величина k (темпа роста валютного курса за весь срок операции), обеспечивающая такую же доходность, что и прямой вклад в рублях, определяется путем приравнивания множителей наращения для альтернативных операций (или из равенства iэфф=i). 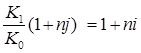 , (148) , (148)откуда 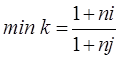 , ,или 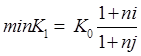 . (149) . (149)Вывод 4: Если ожидаемые величины k или K1 меньше своих критических значений, то операция явно убыточна (iэфф<0). Минимально допустимая величина k (темпа роста валютного курса за весь срок операции), обеспечивающая такую же доходность, что и прямой вклад в рублях, определяется путем приравнивания множителей наращения для альтернативных операций (или из равенства iэфф=i). Вывод 5: Депозит рублевых сумм через конвертацию в валюту выгоднее рублевого депозита, если обменный курс в конце операции ожидается больше min K1. Конвертация валюты и начисление сложных процентов. Рассмотрим совмещение конвертации валюты и наращение сложных процентов. Ограничимся одним вариантом: Вариант: валюта → рубли → рубли → валюта. Три этапа операции записываются в одной формуле для наращенной суммы: 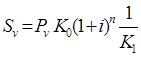 , (150) , (150)где i– ставка сложных процентов. Множитель наращения: 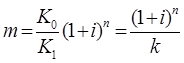 , (151) , (151)где Определим доходность операции в целом в виде годовой ставки сложных процентов iэ. Из формулы наращения по сложным процентам: следует, что: 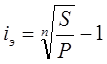 . (152) . (152)Подставив в эту формулу значение Sv, получим: 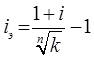 . (153) . (153)Из этого выражения видно, что с увеличением темпа роста k эффективность iэ падает. Это показано на графике рис. 4. 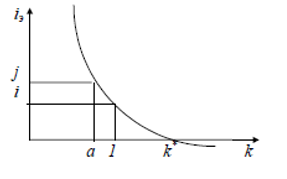 Рис. 4. Анализ показывает, что при k=1 iэ=i, при k>1 iэ Вывод 6: Если ожидаемые величины k или K1 больше своих критических значений, то рассматриваемая операция с двойной конвертацией явно убыточна (iэ<0). Максимально допустимое значение k, при котором доходность операции будет равна доходности при прямом инвестировании валютных средств по ставке j (т. a на рис. 4), находится из равенства соответствующих множителей наращения: 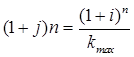 , (154) , (154)откуда: 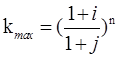 . .Вывод 7: Депозит валюты через конвертацию в рубли выгоднее валютного депозита, если обменный курс в конце операции ожидается меньше max K1. Пример 15. Курс доллара вырос с 79,20 до 79,50 руб. Как изменилась доходность экспортной операции, если при прежнем обменном курсе она равнялась 35 % годовых и на ее осуществление требовалось 15 дней? Временная база К=365. Решение: 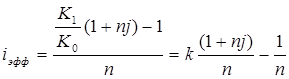 . .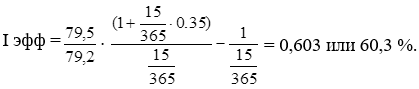 iэфф = 0,603 или 60,3 %. Пример 16. Курс доллара вырос с 29,20 до 29,50 руб. Как изменилась доходность импортной операции, если при прежнем обменном курсе она равнялась 35 % годовых и на ее осуществление требовалось 15 дней? Временная база К=365. Решение: 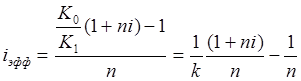 . .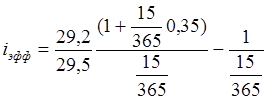 . .i эфф = 0,15 или 15 %. Пример 17. Доллары были приобретены по курсу 29,8 руб. /долл. и через 1,2 года проданы по курсу 29,0 руб./долл., (35,3 руб./долл.). Темп инфляции за этот период времени составил 12 %. Определить доходность финансовой операции. Решение: Для приведенных данных отношение курса продажи к курсу покупки составит: 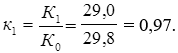 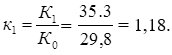 Индекс цен за l,2 года равен: Jр = 1+0,12= 1,1 2. Доходность для рассматриваемых случаев: 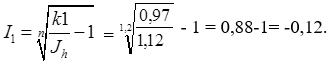 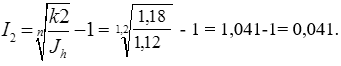 |
