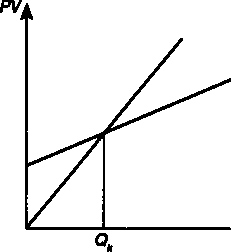Е. М. Четыркин финансовая математика

• Название: Е. М. Четыркин финансовая математика
• Анкор: chetyrkin_e_m_finansovaya_matematika.doc
• Дата: 22.04.2017
• Размер: 4.63 Mb.
• Имя файла: chetyrkin_e_m_finansovaya_matematika.doc
• Тип: Учебник; #4971
• страница: 11 из 58

§7.4. Влияние неопределенности в исходных данных на положение барьерной точки

Барьерное значение выпуска продукции определялось выше для линейной и нелинейной моделей при условии, что все ис­ходные данные установлены однозначно. В этой ситуации по-

158

лучают только одно расчетное значение выпуска. В действи­тельности все не так просто. Так, цену продукции, вероятно, можно с большей надежностью определить для будущего про­изводства в виде некоторого интервала р' + р". Обратившись к линейной модели, получим для этой ситуации интервал значе­ний барьерного выпуска продукции Q'_k— Q"_k(см. рис. 7.7). Аналогичное можно сказать и об остальных параметрах в фор­муле (7.3). Таким образом, при условии, что неоднозначными являются постоянные или переменные затраты, получим диапа­зоны барьерных показателей выпуска для линейной модели (см. рис. 7.8, 7.9).

На рис. 7.10 иллюстрируется совместное влияние неопреде­ленности в цене продукции и переменных затрат на положение барьерного выпуска продукции.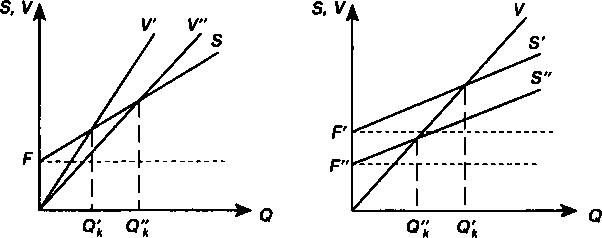

Рис, 7,7 Рис, 7,8

В свою очередь неоднозначность ожидаемой цены продукта и постоянных затрат приводит к результату, который показан на рис. 7.11.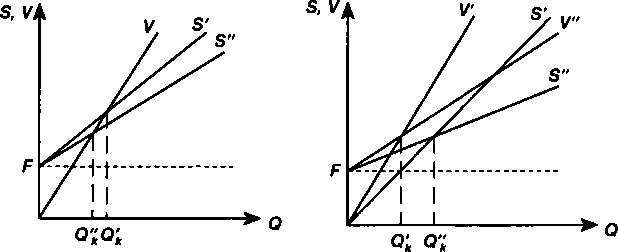



Рис, 7,9 Рис, 7,10

159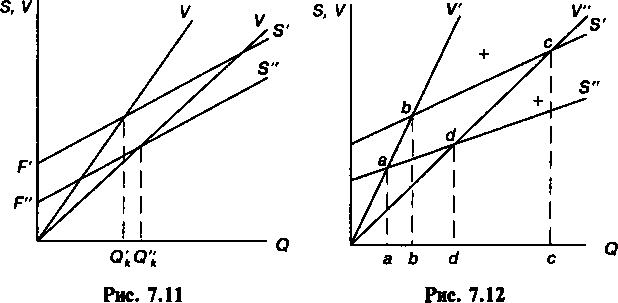



На рис. 7.12 иллюстрируется ситуация, при которой интер­валами заданы все три параметра. На рисунке показаны четыре критических точки: а, Ь, с, d, причем точка а соответствует ми­нимальным затратам и максимальной цене, точка Ь — макси­мальным затратам и цене, точка с — максимальным затратам и минимальной цене, наконец, точка d — минимальным затратам и цене. В зависимости от выдвинутых предположений можно получить ряд диапазонов для барьерной точки: а + b, a + с и т.д.

Что касается методов определения интервалов для значений параметров, то в большинстве случаев вполне оправданно экс­пертное их оценивание.

Интервалы можно установить и в рамках сценарного подхода. В этом случае определяется набор параметров для некоторой совокупности условий (сценария). Обычно разрабатывают оп­тимистический, пессимистический и наиболее вероятный сце­нарии. Оптимистический и пессимистический сценарии позво­ляют определить крайние значения искомой величины. Наибо­лее вероятный сценарий дает промежуточную оценку этой ве­личины. Задание параметров, характеризующих некоторую про­изводственную систему, в виде интервалов дает более полное представление о реально ожидаемых результатах.

§7.5. Барьерные точки выпуска — финансовый подход к их определению

Постановку задачи по определению барьерного объема вы­пуска продукции можно расширить, учитывая дополнительные условия. Представим себе, что разрабатывается проект создания

160

предприятия по производству некоторого нового вида продук­ции. Выпуск продукции намечен в течение п лет в равных объ­емах по годам. Что касается затрат, то сохраняется их деление на постоянные (не связанные с объемами производства) и пе­ременные, пропорциональные выпуску продукции. Текущие за­траты и поступления от реализации продукции можно предста­вить в виде потоков платежей. Здесь возможны два конкуриру­ющих подхода к определению барьерного выпуска. В первом, который условно назовем бухгалтерским, инвестиции не при­нимаются во внимание непосредственно — они учитываются через амортизационные отчисления. Последние включают в те­кущие затраты. Во втором, финансовом, подходе инвестиции иг­рают ключевую роль — выступают в качестве самостоятельного фактора — в то время как амортизация не учитывается в теку­щих расходах. Как видим, оба способа избегают двойного сче­та по отношению к инвестиционным затратам.

Оба способа применяются на практике, однако они дают раз­ные результаты. Начнем с бухгалтерского подхода, согласно кото­рому необходимо определить тот минимальный объем выпуска, при котором затраты окупятся. Иначе говоря, сохраняется ориен­тация на прибыль. Найдем размер прибыли для отдельного года:

P = pQ{cQ+f+d),(7.11)

где р и с имеют тот же смысл, что и выше (см. § 7.1), /•— по­стоянные расходы за год, d — сумма амортизационных списа­ний за тот же период (d = const).

Барьерный объем выпуска продукции составит:

f+d

<Ь-Т=7-^(7Л2)

что, по существу, совпадает с формулой (7.3). Отличие от пос­ледней только в выделении в числителе в качестве самостоя­тельного слагаемого суммы амортизационных расходов.

Если принять во внимание тот факт, что выпуск продукции (поступления дохода) и затраты представляют собой потоки платежей, то "конкурирующие" функции определяются как со­временные стоимости потоков, а именно:

PV(pQ)n PV(f+ d+ cQ\ где PV"■— оператор определения современной стоимости.

161

На основе этих функций получим равенство

PVipQd^PVif+d+cQj.

Решение данного уравнения¹ относительно критического объема выпуска приводит к формуле, аналогичной (7. 12).

Графическая иллюстрация положения барьерной точки вы­пуска представлена на рис. 7.13.

PV(pQ)



> Q

PV(f + d + cQ)

Рис. 7.13

ПРИМЕР 7.6. Исходные данные: п= 5, d = 50, f = 20, р = 50, с = 30. Находим

_Л 20 + 50 _ос Оь = ——— = 35. * 50-30

Проверим этот результат, для чего определим современные стоимости денежных поступлений и затрат для барьерного выпу­ска. Для дисконтирования примем / =15%, Находим а_5;15 = = 3,35216. После чего получим

РО*^а5;15<^{1 + /})°⁵ = 50 х 35 х 3,35216 х 1.15⁰⁵ = 629,

(f + d + cO_k)a₅._i5(1 + /)⁰⁵ = (20 + 50 + 30 х 35)3,35216 х 1.15⁰⁵ =

= 629.

Предположим теперь, что все участвующие в расчете удель­ные характеристики изменяются во времени, т.е. вместо р, с, /, d имеем р_р с_рf_p d_rПеременные параметры, вероятно, более адек-

См. Математическое приложение к главе.

162

ватны реальности. Например, затраты на производство могут расти в связи с увеличением расходов на ремонт по мере износа оборудования, в то же время постоянные затраты могут умень­шаться и т. д. Исходное равенство в этом случае имеет вид:

2(/,+4)И'+е*2^с'^у"'-&2/>у\

/ tt

Отсюда

_пS(/,»4)v*

^g*"v ». v ">• ⁽⁷¹³⁾

ПРИМЕР 7.7. В таблице приведены исходные данные для расче­та барьерного выпуска. Все параметры кроме сумм амортизации здесь переменные величины.

t	Р	С	1	d
1	50	28	20	30
2	50	28	20	30
3	46	30	16	30
4	46	30	16	30
5	42	31	12	30

Для дисконтирования применим процентную ставку 15%. Не­обходимые для расчета по формуле (7.13) данные приведены в следующей таблице.

t	V"	f + d	(f + djv"	pvn	cv"
1	0,93250	50	46,62500	46,625000	26,11000
2	0,81087	50	40,54350	40,54350	22,70436
3	0,70511	48	32,43506	33,84528	21,15330
4	0,61314	45	28,20444	27.59130	18,39420
5	0,53316	42	22,39284	22,39283	16,52804
	Итого	—	170,20008	170,99791	104.8899

На основе табличных данных получим

°^к171 - 104,89 ^2,5У*

Перейдем к финансовому методу, который, повторяем, в от­личие от бухгалтерского учитывает размер капитальных вложе­ний, осуществленных для реализации проекта, и поток чистых

163

поступлений (доходов) без учета амортизационных отчислений. Поток платежей в случае, когда удельные характеристики по­стоянны, отражается следующим рядом:

K,(p-c)Q-f₉(p-c)Q -/...,

где К — размер инвестиций.

Современная стоимость такого потока представляет собой чистый приведенный доход (NPV) — важный показатель, с кото­рым имеют дело в анализе производственных инвестиций (см. гл. 12). В принятых здесь обозначениях и с привязкой чистых поступлений к середине соответствующих периодов можно за­писать:

NPV= -* + [(р - с)0 -/]*„.. (1 + О⁰⁵. По определению в барьерной точке NPV= 0. Отсюда


,0,5
Q_k =

р-^с\^а_пЛ^{х +1}У

₄

(7.14)

Первое слагаемое в скобках равно члену финансовой ренты, современная стоимость которой равна сумме инвестиций.

Поток чистых поступлений можно расчленить без потери в точности для последующих расчетов на два потока: поступле­ний (положительные величины) и расходов (отрицательные ве­личины). Графическая иллюстрация динамики современных стоимостей указанных потоков в зависимости от объема выпу­ска представлена на рис. 7.14.

PV(cQ + f)

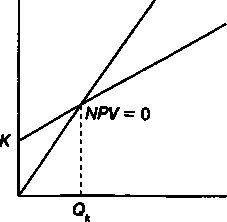^pvk

PV(pQ)

> О


164

Рис. 7.14

ПРИМЕР 7.8. Применим оба метода анализа, бухгалтерский и финансовый, для анализа инвестиционного проекта, который ха­рактеризуется следующими данными: К= 1100, р = 50, с = 30, f = 5, d = 100, п= 10 лет. Дисконтирование осуществляется по ставке 12% годовых.

По формуле (7.12) находим

105 50-30
о* = -^—^г=⁵'²⁵-

В свою очередь финансовый метод дает

1 ( 1100 \

°*""й^»! а_10;12х 1,12С5 +5] = 9,45.

Как видим, последний ответ существенно отличается от пре­дыдущего.

При сравнении формул (7.12) и (7.14) становится очевид­ным, что расхождение в результатах оценки барьерной точки выпуска связано с тем, что

a_n;i(\ +0°-⁵

> d.

Иначе говоря, член ренты, погашающей капиталовложения, должен быть больше амортизационных отчислений. Равенство в приведенном соотношении будет наблюдаться только в слу­чае, когда / = 0. В этом случае а_п.₀ = я.

При бухгалтерском подходе из поля зрения аналитика про­падает выгода от возможного иного использования ресурсов. В связи с этим введем важное в современной экономике понятие условной (вмененной) потери (opportunity costs), связанной с аль­тернативными издержками в результате неиспользования воз­можного альтернативного курса действий. Для иллюстрации приведем следующий пример. Пусть этим ресурсом для кон­кретности является производственное здание. У владельца име­ются две альтернативы его использования:

• 
  осуществить некоторый производственный проект, преду­сматривающий использование этого здания,
  
• 
  продать здание (или сдать его в аренду).
  

Если владелец реализует проект, то он теряет вторую воз­можность получения дохода. Таким образом, хотя при реализа-

165

ции проекта здание не приобретается, его стоимость должна включаться в инвестиционные издержки. Здесь уместно приве­сти следующую иллюстрацию. Компания Локхид обратилась в 1971 г. в Конгресс США по поводу убыточности производства военных самолетов TriStar L—1011. Обращение аргументирова­лось тем, что коммерческая привлекательность производства была определена с учетом барьерной точки выпуска в размере около 200 самолетов. Однако эта величина не учитывала ранее сделанных капиталовложений в сумме 1 млрд долл. С учетом указанных вмененных затрат барьерная точка повышается до 500 самолетов.

Математическое приложение к главе

Доказательство формулы (7.12)

Найдем барьерную точку выпуска для условия, согласно ко­торому современная стоимость доходов равна современной сто­имости затрат. При расчете современных стоимостей полагаем, что выпуск и реализация продукции равномерно распределены в пределах года. В связи с этим без заметной потери точности в расчетах отнесем эти величины к серединам соответствующих лет. В терминах финансовой математики соответствующие по­токи представляют собой постоянные годовые ренты с платежа­ми в середине периодов (см. § 6.3). Пусть PV— оператор опре­деления современной стоимости соответствующего потока пла­тежей. Современная стоимость потока переменных и постоян­ных затрат, в которые включены и амортизационные начисле­ния, в этом случае составит:

PV(f+ d+ cQ) = (/•+ d + cQ)v⁰⁵+ ... +

(1) + (/> d + cQ)v^⁵= (/•+ d + cQ)a_n;i(1 + /)4

где а_пЛ— коэффициент приведения постоянной ренты, v — дисконтный множитель.

В свою очередь современная стоимость поступлений нахо­дится как

PV(pQ) = pQv⁰*⁵+ pQv¹⁵+ ... + pQv"-^ =

(2)

⁼ />e%(i + o⁰'⁵.

166

Из равенства

(/•+ d + cQ_k)a_n;i(1 + if* = _PQ_ka_n;i(\ + О⁰'⁵ следует искомая формула

* /? — с

Глава 8 РИСК И ДИВЕРСИФИКАЦИЯ

§8.1 Риск

В финансовом анализе производственных инвестиций мы неизбежно сталкиваемся с неопределенностью, неоднозначно­стью показателей затрат и отдачи. В связи с этим возникает проблема измерения риска и его влияния на результаты инве­стиций. Поскольку вопросы, связанные с измерением риска в экономической деятельности, рассмотрены в отечественной ли­тературе явно недостаточно, остановимся на них более подроб­но, чем, возможно, это необходимо для раскрытия основной те­мы данной работы.

Широко распространенный термин "риск", как известно, понимается неоднозначно. Его содержание определяется той конкретной задачей, где этот термин используется. Достаточно просто перечислить такие понятия как кредитный, валютный, инвестиционный, политический, технологический риски, риск ликвидности активов и т.д. Отметим, что даже самое общее оп­ределение этого понятия не оставалось неизменным во време­ни. Говоря о первом в экономике научном определении риска, обычно ссылаются на Ф. Найта (1921), который предложил раз­личать риск и неопределенность. Риск имеет место тогда, когда некоторое действие может привести к нескольким взаимоис­ключающим исходам с известным распределением их вероятно­стей. Если же такое распределение неизвестно, то соответству­ющая ситуация рассматривается как неопределенность. Как нам представляется, здесь речь идет, скорее, не об определении риска, а лишь о наличии информации, характеризующей риск.

В экономической практике, особенно финансовой, обычно не делают различия между риском и неопределенностью. Чаще всего под риском понимают некоторую возможную потерю, вы­званную наступлением случайных неблагоприятных событий. В некоторых областях экономической деятельности сложились

168

устойчивые традиции понимания и измерения риска. Наиболь­шее внимание к измерению риска проявлено в страховании. Объяснять причину такого внимания нет необходимости. Изме­ритель риска, как возможная потеря страховщика, был исполь­зован еще в конце XVIII в. В других направлениях финансовой деятельности под риском также понимается некоторая потеря. Она может быть объективной, т.е. определяться внешними воз­действиями на ход и результаты деятельности хозяйствующего субъекта. Так, например, потеря покупательной способности денег (инфляционный риск) не зависит от воли и действий их владельца. Однако, часто риск, как возможная потеря, может быть связан с выбором того или иного решения, той или иной линии поведения. Заметим также, что в некоторых областях де­ятельности риск понимается как вероятность наступления не­которого неблагоприятного события. Чем выше эта вероят­ность, тем больше риск. Такое понимание риска оправданно в тех случаях, когда событие может наступить или не наступить (банкротство, крушение и т.д.).

Когда невозможны непосредственные измерения размеров потерь или их вероятностей, риск можно квантифицировать с помощью ранжирования соответствующих объектов, процессов или явлений в отношении возможного ущерба, потерь и т.д. Ранжирование обычно основывается на экспертных суждениях.

Естественной реакцией на наличие риска в финансовой де­ятельности является стремление компенсировать его с помо­щью так называемых рисковых премий (risk premium), которые представляют собой различного рода надбавки (к цене, уровню процентной ставки, тарифу и т.д.), выступающие в виде "платы за риск". Второй путь ослабления влияния риска заключается в управлении риском. Последнее осуществляется на основе различ­ных приемов, например, с помощью заключения форвардных контрактов, покупки валютных или процентных опционов и т.д.

Одним из приемов сокращения риска, применяемым в инве­стиционных решениях, является диверсификация, под которой понимается распределение общей инвестиционной суммы меж­ду несколькими объектами. Диверсификация — общепринятое средство сокращения любого вида риска. С увеличением числа элементов набора (портфеля) уменьшается общий размер рис­ка. Однако только в случае, когда риск может быть измерен и представлен в виде статистического показателя, управление ри­ском получает надежное основание, а последствия диверсифи-

169

кации поддаются анализу с привлечением методов математиче­ской статистики.

В инвестиционном анализе и страховом деле риск часто из­меряется с помощью таких стандартных статистических харак­теристик, как дисперсия и среднее квадратическое (стандартное) отклонение. Обе характеристики измеряют колебания, в данном случае — колебания дохода. Чем они больше, тем выше рассе­яние показателей дохода вокруг средней и, следовательно, сте­пень риска.

Напомним, что между дисперсией (D) и средним квадрати-ческим отклонением (а) существует следующее соотношение:

а» V/>.

В свою очередь дисперсия относительно выборочной сред­ней (х) находится как

п - 1

где п — количество наблюдений, х — средняя случайной пере­менной х.

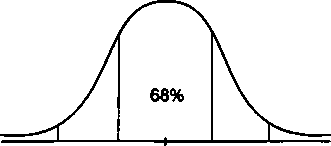
-2а -а х +а +2а

Рис. 8.1

170

Как известно, среднее квадратическое отклонение имеет то неоспоримое достоинство, что при близости наблюдаемого рас­пределения (например, распределении дохода от инвестиций) к нормальному, что, строго говоря, должно быть статистически проверено, этот параметр может быть использован для опреде­ления границ, в которых с заданной вероятностью следует ожи­дать значение случайной переменной. Так, например, с вероят­ностью 68% можно утверждать, что значение случайной пере­менной х (в нашем случае доход) находится в границах х ± a, a с вероятностью 95% — в пределах х ± 2а и т.д. Сказанное ил­люстрируется на рис. 8.1

§8.2. Диверсификация инвестиций и дисперсия дохода

Определим теперь что дает диверсификация для уменьшения риска и выявим условия, когда эта цель достигается. В качестве объекта анализа примем некоторый абстрактный портфель цен­ных бумаг (далее для краткости — портфель). Такой выбор объ­ясняется методологическими преимуществами — в этом случае проще выявить зависимости между основными переменными. Однако многие из полученных результатов без большой натяж­ки можно распространить и на производственные инвестиции.

В предыдущем параграфе отмечалось, что в качестве измери­теля риска в долгосрочных финансовых операциях широко рас­пространена такая мера, как дисперсия дохода во времени. Ди­версификация портфеля при правильном ее применении при­водит к уменьшению этой дисперсии при всех прочих равных условиях. Диверсификация базируется на простой гипотезе. Ес­ли каждая компонента портфеля (в рассматриваемой задаче — вид ценной бумаги) характеризуется некоторой дисперсией до­хода, то доход от портфеля имеет дисперсию, определяемую его составом. Таким образом, изменяя состав портфеля, можно ме­нять суммарную дисперсию дохода, а в некоторых случаях свести ее к минимуму.

Итак, пусть имеется портфель из п видов ценных бумаг. До­ход от одной бумаги вида / составляет величину d_rСуммарный доход (А), очевидно, равен

A = 2a.d_i9(8.1)

где a_i— количество бумаг вида /.

Если d_iпредставляет собой средний доход от бумаги вида /, то величина А характеризует средний доход от портфеля бумаг в целом.

Для начала положим, что показатели доходов различных ви­дов бумаг являются статистически независимыми величинами (иначе говоря, не коррелируют между собой). Дисперсия дохо­да портфеля (обозначим ее как D) в этом случае находится как

Я-£*?А. (8.2)

/-1

171

где D. — дисперсия дохода от бумаги вида /, п — количество видов ценных бумаг.

Для упрощения, которое нисколько не повлияет на резуль­таты дальнейших рассуждений, перейдем от абсолютного из­мерения количества ценных бумаг к относительному. Пусть теперь а. характеризует долю в портфеле бумаги вида /, т.е. О < а. < 1, 21а. = 1.

Для зависимых в статистическом смысле показателей дохода отдельных бумаг дисперсию суммарного дохода находим следу­ющим образом:

^D" % ^at^{Di+ 2} 2 ^ai^aJ^rU°i°J>

(8.3)

где D_f— дисперсия дохода от бумаги вида /, r_fJ— коэффициент корреляции дохода от бумаг вида / и у, а_у ис^.- среднее квад-ратическое отклонение дохода у бумаг вида / и у.

Коэффициент корреляции двух случайных переменных х и у, как известно, определяется по формуле¹

^г*у =

%(х-х)(у- у)

па_хо_у

(8.4)

где х, у — средние (в нашем случае средние доходы двух видов бумаг).

Для расчетов часто применяется следующая рабочая формула:

^пУ*у-У*Уу

'ху

_{2*ЧХ*Пк>Ч5>)}

Поскольку коэффициент корреляции может быть как поло­жительной, так и отрицательной величиной, то, как это выте­кает из (8.3), при положительной корреляции дисперсия суммарно-

¹ Напомним следующие свойства коэффициента корреляции:

• 
  коэффициент не имеет размерности, следовательно, он сопоставим для разных рядов данных;
  
• 
  величина г_хулежит в пределах от -1 до +1. Значение г_ху= +1 говорит о том, что между переменными существует полная положительная корреляция, т. е. наблюдается функциональная линейная зависимость — с увеличением х ли­нейно растет у. При г_ху= -1 наблюдается отрицательная линейная зависимость.
  

172

го дохода увеличивается, при отрицательной она сокращается. В самом деле, при заметной отрицательной корреляции положи­тельные отклонения от среднего дохода одних бумаг погашают­ся отрицательными отклонениями у других. И наоборот, при положительной корреляции отклонения суммируются, что уве­личивает общую дисперсию и риск.

Проследим теперь, каково влияние масштаба диверсифика­ции на размер риска. Под масштабом диверсификации здесь бу­дем понимать количество объектов, выбранных для инвестиции (количество видов ценных бумаг). Обратимся к условному при­меру, который позволяет наиболее отчетливо выделить влияние указанного фактора. Итак, пусть портфель состоит из бумаг различного вида, но имеющих одинаковую дисперсию дохода (о^). Удельные веса в портфеле каждого вида бумаг также оди­наковы, а общая сумма вложений равна 1. Положим, что пока­затели доходности у отдельных видов бумаг статистически не­зависимы, т.е. применима формула (8.2). В этих условиях для оценки величины среднего квадратического отклонения дохода портфеля получим

п °'

где п — количество видов ценных бумаг.

Воспользуемся приведенной формулой и определим диспер­сию дохода для портфеля, состоящего из двух и трех видов бу­маг. Так, для двух бумаг имеем

^D- 2°о ^{и а}"^2°° "°'^71а°-

Для трех видов бумаг квадратическое отклонение портфеля составит 0,58а₀. Таким образом, с увеличением числа составляю­щих портфеля риск уменьшается даже при одинаковой диспер­сии составляющих элементов. Однако прирост действенности диверсификации уменьшается. Соответствующая зависимость изображена на рис. 8.2.

Как видим, наибольшее влияние увеличение масштабов ди­версификации оказывает на начальных стадиях, т.е. при малых значениях я. Например, в рамках рассмотренного примера пе­реход от одного вида бумаг к четырем сокращает квадратиче­ское отклонение на 50%, а от одного к восьми — на 65%.

173

Рис. 8.2

Полученные выше выводы в отношении тенденции измене­ния среднего квадратического отклонения в зависимости от числа составляющих при условии, когда дисперсии составляю­щих одинаковы, очевидно, справедливы и для более общих слу­чаев. Однако, зависимость этих параметров от степени диверси­фикации проявляется здесь не столь четко.

Посмотрим теперь, как изменяются доход и величина риска при изменении структуры портфеля. Для этого вернемся к фор­мулам (8.2) и (8.3) и запишем их только для двух видов бумаг (X и Y). Такой анализ вряд ли имеет практическое значение. Однако с его помощью наглядно демонстрируются последствия "смешения" ценных бумаг с различными доходностью и дис­персией. Для независимых доходов получим

D = a²D' + a²D_v,(8.5)

и для зависимых доходов

D= сРо²+ а² о²+ 2а а г о о . (8.6)

**ххУ У^хУ *У ^х Уv"-^v/

Причем а_у= 1 — а_х.

В этом случае среднее значение суммарного дохода опреде­ляется как

Л = a_xd_x+ (1 - a_x)d_y.(8.7)

Пусть d_y > d_xи о_у > о_х. Очевидно, что в силу этих условий рост доли бумаг второго вида увеличивает доходность портфе­ля. Так, на основе (8.7) получим

Л = d_y+ (d_y- d_x)a_y.(8.8)

Что касается дисперсии дохода портфеля, то, как это следу­ет из (8.6), положение не столь однозначно и зависит от знака

174

и степени корреляции. В связи с этим подробно рассмотрим три ситуации: полная положительная корреляция доходов (г = = +1), полная отрицательная корреляция (г = -1), независи­мость доходов или нулевая корреляция (г = 0).

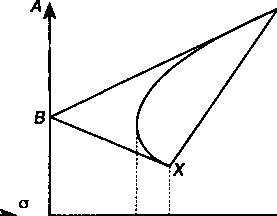
В первом случае увеличение дохода за счет включения в порт­фель бумаги вида У помимо X сопровождается ростом как дохо­да, так и дисперсии. Для портфеля, содержащего оба вида бумаг, квадратическое отклонение находится в пределах о_х < о < о (см. рис. 8.3, где точка X означает портфель, состоящий только из бумаг вида Л, а К— портфель из бумаг вида Y).

Для частного случая, когда о_х= о_у= а, получим по формуле (8.6) D = а². Иначе говоря, при полной положительной корре­ляции "смешение" инвестиций не окажет никакого влияния на величину дисперсии.

При полной отрицательной корреляции доходов динамика квадратического отклонения доходов от портфеля более слож­ная. По мере движения от точки Л" к точке К эта величина сна­чала сокращается и доходит до нуля в точке В, затем растет (см. рис. 8.4). Следует обратить внимание на то, что при движении от Л" до В рост дохода сопровождается уменьшением риска (квадратического отклонения).

В последней из рассматриваемых ситуаций квадратическое отклонение при увеличении доли бумаги К проходит точку ми­нимума, равного а_т, далее оно растет до о_у(см. рис. 8.5). (Проблема определения состава портфеля, при котором дости­гается минимум дисперсии, обсуждается в следующем парагра­фе.)

Совместим теперь все три графика на одном (см. рис. 8.6.) Как видим, все возможные варианты зависимости "доход— С КО" находятся в треугольнике XBY.

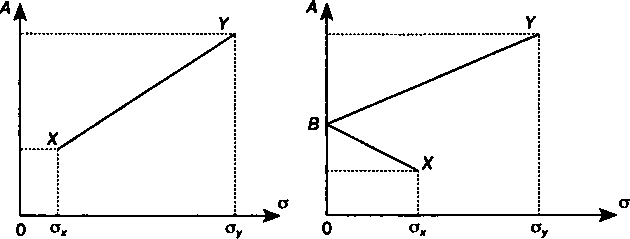
Рис. 8.3

Рис. 8.4

175

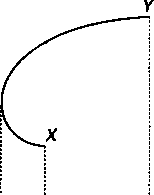
о
О о_то_х о_у"О о_то_хо_у

Рис. 8.5 Рис. 8.6

Из сказанного непосредственно следует, что эффективность диверсификации (в отношении сокращения риска) наблюдает­ся только при отрицательной или, в крайнем случае, нулевой корреляции.

ПРИМЕР 8.1. Портфель должен состоять из двух видов бумаг, параметры которых: d_x= 2; о_х= 0,8; d = 3; о = 1,1.

Доход от портфеля: А = 2а_х+ За_у. Таким образом, доход в за­висимости от величины долей находится в пределах 2 < А < 3.

Дисперсия суммы дохода составит:

D = а^0,8² + а*1,1² + a^r^O.8 x 1,1.

Определим доход и дисперсию для портфеля с долями, рав­ными, допустим, 0,3 и 0,7. Получим по формулам (8.6) и (8.7): D = 0,651 + 0,37/-^ и А= 2,7. Таким образом, при полной поло­жительной корреляции D = 1,021, при полной отрицательной кор­реляции D = 0,281. В итоге с вероятностью 95% можно утвер­ждать, что суммарный доход находится в первом случае в преде­лах 2,7 ± 2 х ^|^_t02^ « 2,7 ± 2,02; во втором — он определяется пре­делами 2,7 ± 2 х д/о,281 * 2,7 ± 1,06. При нулевой корреляции до­ходов искомые пределы составят 2,7 ± 2^/0,651 * 2,7 ± 1,64.

Продолжим анализ с двумя бумагами и проследим, как влия­ет включение в портфель безрисковой (risk free) инвестиции¹.

¹ В странах со стабильной экономикой безрисковой обычно считается цен­ная бумага, выпущенная государственным казначейством.

176

Для этого заменим в портфеле бумагу К с параметрами d_y9 o_yна бумагу с такой же доходностью, но с нулевой дисперсией. До­ходность портфеля от такой замены, разумеется, не изменится. Что же касается дисперсии, то она теперь составит:

0=0*0*.

X X

Дисперсия дохода портфеля теперь зависит от удельного ве­са безрисковой составляющей, так как

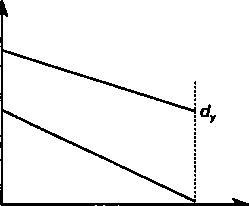
Таким образом, "разбавление" портфеля безрисковой бума­гой снижает риск портфеля в целом, а квадратическое отклоне­ние дохода портфеля определяется убывающей линейной функ­цией доли безрисковой бумаги. Если d_x > d_y(в противном слу­чае проблема выбора портфеля отпадает — он должен состоять только из безрисковых бумаг), то доход от портфеля по мере увеличения доли безрисковой бумаги уменьшается от d_xдо d, a величина квадратического отклонения сокращается от о_хдо О (см. рис. 8.7). И наоборот, рост доли рисковой бумаги увеличи­вает как риск, так и доход.

А, а d_x

О 1 а_у

Рис. 8.7

Последнее утверждение для портфеля, состоящего из двух видов бумаг, иллюстрируется уравнением (8.10), которое полу­чено преобразованием (8.7):

Л ⁼ ^⁺К4Х- (8Л0)

В свою очередь на основе (8.9) находим

177

В итоге получим интересное соотношение

d - d
А = d+— ^Lo. (8.11)

^У °х

Дробь в приведенном выражении иногда называют рыночной ценой риска. Если эта величина равна, скажем, 0,5, то при ро­сте квадратического отклонения на 1% доход увеличится на 0,5%.

§8.3. Минимизация дисперсии дохода

Приведенные выше выражения для дисперсии суммарного дохода позволяют рассмотреть проблему диверсификации инве­стиций и риска еще в одном аспекте, а именно, — определить структуру портфеля, которая минимизирует дисперсию и, сле­довательно, риск. Для нахождения минимума дисперсии вер­немся к определяющим ее формулам. Если предположить, что нет статистической зависимости между доходами от отдельных видов инвестиций, то найти оптимальную в указанном смысле структуру портфеля не так уж и сложно. Положим, что порт­фель, как и выше, состоит из двух видов бумаг Хи К Их доли в портфеле составляют а_хи 1— а# а дисперсии D_xи D_y. Общая дисперсия определяется по формуле (8.5). Поскольку эта функ­ция является непрерывной, то применим стандартный метод определения экстремума. Находим, что минимальное значение дисперсии суммы имеет место тогда, когда

Формулу (8.12) обычно приводят в аналитической финансо­вой литературе. Однако, для того, чтобы ею можно было вос­пользоваться, необходимо иметь значения дисперсий. По-види­мому, при расчетах на перспективу удобнее оценить или задать экспертным путем отношение дисперсий:

D_x/y=D_x/D_y.(8.13)

178

Разделим теперь числитель и знаменатель (8.12) на D_y, полу­чим

_ъ-тттт-⁽⁸¹⁴⁾

х/у

При наличии корреляции между показателями доходов обра­тимся к (8.6). Минимум этой функции имеет место в случае, когда

D — г о о

°^хD +D -2г оо^{9( }}

х у *'ху х у

или, использовав отношение дисперсий (8.13), получим

^l-^rxyjDx/y,_й -,.

а_х " т—. (8.16)

&х/у ⁺ * " 2^гхуу&х/у

Как видно из приведенных формул, расчетная величина до­ли одной из бумаг может при некоторых условиях оказаться от­рицательной. Отсюда следует, что этот вид бумаги просто не должен включаться в портфель.

ПРИМЕР 8.2. Вернемся к данным примера 8.1 и определим стру­ктуру портфеля с минимальной дисперсией. Напомним, что о_х = 0,8; о_у= 1,1.

При полной положительной корреляции расчетные значения доли первой бумаги составят по формуле (8.15)

1,1²-1 х0,8x1,1 *^х0,8²+ 1,1²-2х 1 х0,8х 1,1

Соответственно, а_у < 0. Следовательно, минимальная диспер­сия имеет место в случае, когда портфель состоит из одной бу­маги вида X. Средний доход от портфеля равен 2.

При полной отрицательной корреляции находим

1,1» - (-1)0,8 ж 1,1 _лс„

д — , ₌ Л k7Q

^х 0,8² - 1,1² - 2(-1)0,8 х 1,1 * * а_у= 1 -0,579 = 0,421.

Дисперсия в этом случае равна нулю (см. рис. 8.4), а средний доход составит 2,421.

179

Наконец, при отсутствии корреляции получим по формуле (8.12) а_х = 0,654; а_у= 1 - 0,654 = 0,346. Дисперсия дохода при такой структуре портфеля равна 0,418, а средний доход равен 2,346.

Пусть теперь портфель состоит из трех видов бумаг X, Y, Z. Их доли а_х, а_уи a_z= 1 - (а_х+ а).Дисперсия дохода от порт­феля при условии независимости доходов от отдельных видов бумаг составит

D = a² DL + a² D + [1 - (а_х+ a_v)]²D₇.

х ху У ^1хУZ

Минимум дисперсии достигается, если структура портфеля определяется следующим образом:

А
У/1


^a* ⁼ -DD.
'x/z "y/z ^{+ D}x/z ^{+ D}y/z

X/Z

^аУ D , D , + D , + D ,

x/z y/z x/z "y/z

He будем останавливаться на ситуации, когда доходы трех видов бумаг статистически зависимы. Перейдем к общей поста­новке задачи и определим структуру портфеля с л составляю­щими. Допустим, что доходы статистически независимы. Опус­тим доказательства¹ и приведем результат в матричном виде:

А = £Г'е,

(8.17)

где е — единичный вектор, характеризующий структуру порт­феля,

1

+ 1

D₂

+ 1

I 1

*»-!

4.-1

D„

180

Доказательства приведены в Математическом приложении к главе.

А -— вектор, характеризующий п — 1 элементов структуры порт­феля.

Матрица D имеет размерность (л — 1) х (л — 1).

ПРИМЕР 8.3. Эксперты оценили следующие отношения диспер­сий для портфеля, состоящего из четырех видов бумаг: D_1/4 = 1,5; D_2/4 = 2; D_3/4 =1. По формуле (8.17) получим

[2,5 1 11	-1	[0,210]
1 3 1	хв-	0,158
| 1 12		0,316

3 ^а4-¹-Ё^а/"¹-⁰'⁶⁸⁴"⁰'³¹⁶-

Заметим, что структуру портфеля, минимизирующую дис­персию дохода, с п составляющими при наличии корреляции определить так же просто, как это было сделано выше, нель­зя. Однако решение существует, хотя его получение достаточ­но хлопотное дело, да и вряд ли оно необходимо для практики.

Анализ диверсификации представляет собой первый этап в исследовании портфеля инвестиций. Следующим является ма­ксимизация дохода. Эта проблема также связана с измерением риска и требует обстоятельного специального обсуждения, вы­ходящего за рамки настоящего учебника. Поэтому ограничим­ся лишь замечанием о том, что метод Г. Марковица, который заключается в разработке и решении специальной модели не­линейного программирования с использованием показателей доходов и дисперсий, в теоретическом плане не вызывает воз­ражений. Что касается его практического применения, то здесь, на наш взгляд, скрыты серьезные подводные камни. За­тронем лишь одну проблему — какой срок для расчета диспер­сий следует принять во внимание? Если ограничиться неболь­шим сроком, то получим наиболее приближенные к современ­ности данные. Однако они могут оказаться неустойчивыми, со­держать много "шума", с другой стороны, стремление охватить максимальный срок неизбежно приведет к устареванию дан­ных.

181

Математическое приложение к главе

Минимум дисперсии дохода при отсутствии корреляции. Дисперсия в этом случае определяется выражением (8.2), ко-

торое для п долей запишем как

я-1

О)

Я- 2*,²4* 1-2*/
i \ \ I

В свою очередь

где

(■-'|*i) -l-22*;+(2*/)²,

/я-1 \² я-1 л-1 я-1

Окончательно имеем

2

/ /1-1 \ Я-1 Я-1 Я-1

Я-1

+ 2в_я-2^-1 ⁺ 2 */

(2)

Преобразуем (1) с использованием (2) и определим л - 1 ча­стных производных:

/'(*i)-*iA +

/я-1 \


/'(«₂)-^₂4|«/-ij^

(3)

182

/'(*«_,)-*„_,/>„_, + 1*/-1

D„.

Разделим каждое уравнение системы (3) на D_nи приравняем его нулю. После некоторых преобразований получим

«|ГБ- ⁺ Ч ⁺ «1 ^{+ в}э ⁺ " ⁺ «.-1-1.

«I +o₂\-^+\\ + a_i + ... + a^_l^l,

(4)


^а\ ^{+ а}2 ^{+ а}Ъ ⁺ —^{+ Д}л

+ i=i.

Представим систему уравнений (4) в матричном виде:

AD=e. После чего получим искомое уравнение (8.17):

А = Dr^xe.

ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА

1. 
   Первозеанский А.А., Первозванская Т.Н. Финансовый рынок: Расчет и Риск. М.: Инфра-М, 1994. § 6.4.
   
2. 
   Венецкий И.Г., Венецкая В.И. Основные математико-статистические понятия и формулы в экономическом анализе. М.: Финансы и статистика, 1979. С. 56-57.
   
3. 
   Касимов Ю.Ф. Основы теории оптимального портфеля ценных бумаг. М.: Филинъ, 1998. Гл. 6, 7.