Е. М. Четыркин финансовая математика

• Название: Е. М. Четыркин финансовая математика
• Анкор: chetyrkin_e_m_finansovaya_matematika.doc
• Дата: 22.04.2017
• Размер: 4.63 Mb.
• Имя файла: chetyrkin_e_m_finansovaya_matematika.doc
• Тип: Учебник; #4971
• страница: 18 из 58

§12.3. Свойства чистого приведенного дохода

Остановимся на особенностях чистого приведенного дохода, важных для его понимания и практического применения. Первое, на что надо обратить внимание, — чистый приведенный доход — это абсолютный показатель и, следовательно, зависит от масшта­бов капитальных вложений. Это обстоятельство необходимо учи­тывать при сравнении нескольких инвестиционных проектов.

Второе — существенная зависимость чистого приведенного дохода от временных параметров проекта. Выделим два из них: срок начала отдачи от инвестиций и продолжительность пери­ода отдачи. Сдвиг начала отдачи вперед уменьшает величину

263

современной стоимости потока доходов пропорционально дис­контному множителю v*, где / — период отсрочки.

ПРИМЕР 12.3. Пусть по каким-либо причинам момент начала от­дачи в примере 12.1 (варианте) отодвигается, скажем, всего на один год. В этом случае

N_A= -214,9 + 377,1 х 1.Г¹ = 127,9.

Теперь этот вариант заметно проигрывает по величине чисто­го приведенного дохода по сравнению с вариантом Б.

Что касается продолжительности периода отдачи, то заме­тим, — чрезмерное его увеличение создает иллюзию повыше­ния полноты и надежности оценки эффективности. Однако размеры отдаленных во времени доходов вряд ли можно считать вполне надежными и обоснованными. Кроме того, затраты и поступления, ожидаемые в далеком будущем, мало влияют на величину чистого приведенного дохода и ими, как правило, можно пренебречь. В связи со сказанным уместно привести следующую иллюстрацию. Пусть речь идет о доходе, поступаю­щем в виде постоянной ренты. Зависимость N от срока ренты п показана на рис. 12.1. В начальный момент N = —/Г. В точке п - а капиталовложения точно окупаются поступившими дохо­дами. По мере увеличения срока поступлений дохода увеличи­вается величина N Однако прирост ее замедляется, а само зна­чение N стремится к некоторому пределу А.

Выбор момента, относительно которого дисконтируются члены потока платежей {focal date), также влияет на величину N. Обычно для этого выбирается начало реализации проекта.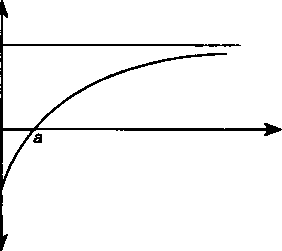

о к

^N\ А

Рис. 12.1

264

Сдвиг вперед момента времени для оценивания N увеличивает абсолютные значения обеих составляющих чистого приведен­ного дохода. Знак у величины N не изменяется при сдвиге мо­мента для оценивания. Заметим также, что предпочтительный вариант проекта остается таковым при любом выборе момента. При сравнении нескольких проектов должно соблюдаться есте­ственное требование — этот момент должен быть общим для всех проектов.

Проследим теперь влияние процентной ставки на величину N Из (12.8) следует, что с ростом ставки приведения размер чи­стого приведенного дохода сокращается. Зависимость N от ставки / для случая, когда вложения осуществляются в начале инвестиционного процесса, а отдачи примерно равномерные, иллюстрируется на рис. 12.2.

Как показано на рисунке, когда ставка приведения достига­ет некоторой величины У, финансовый эффект от инвестиций оказывается нулевым. Ставка У является важной характеристи­кой в инвестиционном анализе. Ее содержание и метод расчета обсуждаются в следующем парафафе. Здесь же отметим, что любая ставка, меньшая чем У, приводит к положительной оцен­ке N (точки а и Ь), и наоборот, дисконтирование по ставке вы­ше У дает отрицательную величину чистого приведенного дохо­да (точка с) при всех прочих равных условиях. Как видим, из­менение ставки приведения оказывает заметное влияние на аб­солютную величину N Например, для условий, согласно кото­рым инвестиции осуществляются равномерно в течение трех лет, ежегодно по 100, а доходы будут поступать 7 лет также по 100 денежных единиц, находим следующие значения N в зави­симости от уровня процентной ставки:

N

N_a

N_k

a b

Рис. 12.2

265

i 5 10 15 20

N220,8 105,0 28,8 -22,2

Нулевая величина чистого приведенного дохода в этом при­мере имеет место при условии / = У = 17,5 %.

Картина рассматриваемой зависимости резко изменяется, если члены потока платежей меняют знаки больше одного раза. Например, в силу того, что через определенное количество лет после начала отдачи предусматривается модернизация произ­водства, требующая значительных затрат. В этом случае кривая зависимости N от / будет заметно отличаться от кривой на рис. 12.2. Так, на рис. 12.3 показана ситуация, когда величина N три­жды меняет свой знак.

Влияние размеров затрат и доходов на N очевидно. Величи­на N находится в линейной зависимости от каждого из указан­ных показателей. Причем, чем отдаленнее срок поступления или затрат, тем меньше это влияние.

Теперь остановимся на сравнении (ранжировании) несколь­ких вариантов проекта по величине N. На первый взгляд пред­ставляется, что такое сравнение весьма условно, так как N за­висит от уровня ставки. Однако, итог ранжирования проектов обладает высокой устойчивостью (инвариантностью) по отно­шению к ставке приведения. Для пояснения обратимся к слу­чаю, когда сравниваются три проекта. Обозначим их как А, Б и В. Капиталовложения во всех случаях мгновенные, а потоки до­ходов представляют собой постоянные ренты постнумерандо с одинаковыми сроками, но разными размерами отдачи. Потоки платежей и расчетные значения N и J показаны в табл. 12.1. При расчете N применена ставка 12 %.

N



Рис. 12.3

266

Таблица 12.1

t	A	Б	В
0 1 2 10	-20 5 5 5	-25 7 7 7	-25 6 6 6
N J(%)	8,25 21,4	14,55 25,0	8,90 20,2

Наибольшие значения N и / у варианта 5. Кривые зависи­мости Not /для вариантов Л и Б показаны на рис. 12.4. Как ви­дим, для любых значений / положительные значения N вариан­та Б больше, чем у А. В свою очередь при сравнении вариантов А и В (см. рис. 12.5) обнаруживаем, что чистый приведенный доход по варианту В больше, чем у А при применении любой ставки, вплоть до 15,1 %. Если ставка приведения превышает этот уровень, то места проектов по уровню чистого приведен­ного дохода меняются.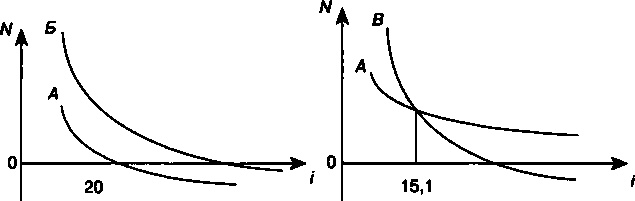



Рис. 12.4 Рис. 12.5

Приведенный пример иллюстрирует тот факт, что выбор про­центной ставки иногда совсем не сказывается на ранжировании проектов. Точка пересечения кривых А и В определяет критиче­скую или барьерную ставку по терминологии седьмой главы.

§12.4. Внутренняя норма доходности

Не менее важным для финансового анализа производствен­ных инвестиций, как и чистый приведенный доход, является внутренняя норма доходности. Под этим критерием понимают такую расчетную ставку приведения, при которой капитализа-

267

ция получаемого дохода дает сумму, равную инвестициям, и, следовательно, капиталовложения только окупаются. Иначе го­воря, при начислении на сумму инвестиций процентов по став­ке, равной внутренней норме доходности (обозначим ее как У), обеспечивается получение распределенного во времени дохода, эквивалентного инвестициям. Чем выше эта норма, тем, разу­меется, больше эффективность инвестиций. Обсуждаемый па­раметр может быть как положительной, так и отрицательной величиной. Последнее означает, что инвестиции не окупаются. Величина этой ставки полностью определяется "внутренними" условиями, характеризующими инвестиционный проект. Ника­кие предположения об использовании чистого дохода за преде­лами проекта не рассматриваются.

Пусть / — приемлемый для инвестора уровень ставки про­цента, — выше она была названа минимально привлекательной ставкой доходности или нормативом доходности. Очевидно, что разность ставок У - / характеризует эффективность инве­стиционной (предпринимательской) деятельности. С чисто фи­нансовых позиций инвестиции имеют смысл только тогда, ко­гда У > /. При У < / нет оснований для осуществления инвести­ций, так как доходность ниже принятого норматива, если же под i понимается стоимость заемных средств, то они просто убыточны.

Расчет внутренней нормы доходности часто применяют в ка­честве первого шага анализа инвестиций. Для дальнейшего ана­лиза отбираются только те проекты, которые обеспечивают не­который приемлемый для данной компании уровень доходно­сти. Последний зависит от многих объективных и субъективных обстоятельств и охватывает весьма большой диапазон возмож­ных значений даже для однородных видов предприятий.

Методы расчетов. В общем случае, когда инвестиции и дохо­ды задаются в виде потока платежей, искомая ставка У опреде­ляется на основе решения уравнения (12.7) относительно v ка­ким-либо методом¹:

JV-0, (12.11)

¹ Напомним, что инвестиции имеют в этом равенстве отрицательный знак, доходы — положительный. Положительное значение J имеем в случае, когда сумма дисконтированных доходов больше размера инвестиций. Если все члены потока имеют один знак, то, естественно, искомую ставку получить нельзя.

268

где v — дисконтный множитель по искомой ставке У; t — вре­мя от начала реализации проекта; R_t— член потока платежей (вложения и чистые доходы).

Затем, зная v, находим искомую ставку У. Расчет искомой ставки осуществляется различными методами, дающими раз­ные по точности ответы. Различаются они и по трудоемкости. В западной учебной литературе часто ограничиваются методом последовательного подбора значения ставки до выполнения ус­ловия N — 0. Действительно, при наличии опыта и сравнитель­но коротком потоке платежей такой подход довольно быстро дает удовлетворительные результаты. Более "серьезные" мето­ды определения У основываются на различных итерационных процедурах. К ним, в частности, относятся метод Ньютона— Рафсона и метод секущей или какие-либо численные процеду­ры.

В пакете Excel содержится программа ВНДОХ, которая поз­воляет определить внутреннюю норму доходности¹ на основе потока платежей с одинаковыми интервалами между членами потока. Инвестиции показываются с отрицательным знаком, доходы — с положительным. Члены потока относят к концам периодов.

Порядок действий при использовании программы ВНДОХ

1. 
   Разместить показатели потока платежей в одной строке или столбце таблицы Excel. Если платежей в периоде нет, то соответствующую ячейку таблицы не заполнять и пе­рейти к следующему периоду.
   
2. 
   Последовательно вызвать: f_x, "финансовые функции", ВНДОХ.
   
3. 
   В строке Значения показать адрес массива данных в табли­це Excel.
   
4. 
   В строке Предположения указать ожидаемое (примерное) значение нормы доходности². Если этот параметр не ука­зывается, то он по умолчанию принимается равным 0,1.
   

¹ В сопровождающем программу тексте этот показатель ошибочно назван
"скоростью оборота".

² Для определения внутренней нормы доходности применяется итерацион­
ный процесс, поэтому желательно указать некоторое ориентировочное началь­
ное значение ставки.

269

После выполнения действий 1—3 в итоговой строке Значе­ние автоматически показывается расчетная величина внутрен­ней нормы доходности. После нажатия кнопки ОК эта величи­на показывается в выделенной ячейке таблицы Excel

Примечание. Пользователь может изменять размеры членов потока платежей, не выходя из таблицы Excel.

Чистый приведенный доход при условии, что дисконтирова­ние членов потока производится по ставке У, по определению равен нулю (см. рис. 12.2). На этом рисунке кривая пересекает ось / только один раз в точке У. Это типовой случай. Однако — об этом уже упоминалось выше — при специфическом распре­делении членов потока во времени последовательные члены по­тока платежей могут изменять свой знак несколько раз (напри­мер, если ожидаются в будущем крупные затраты на модерни­зацию процесса производства). В этих случаях кривая пересека­ет эту ось несколько раз (см. рис. 12.3). Соответственно, имеет­ся несколько значений искомой ставки (несколько корней мно­гочлена), удовлетворяющих условию (12.7). Заметим, что усло­вие смены знаков является необходимым, но недостаточным для получения нескольких корней.

N

Рис. 12.6

В редких, но теоретически возможных, случаях чистый при­веденный доход оказывается положительной величиной при любом значении ставки / (см. рис. 12.6). Величина У здесь про­сто отсутствует. Если имеется множественность значений У или значение отсутствует, то при сравнении нескольких инвестици­онных проектов следует воспользоваться другими измерителя­ми эффективности.

270

ПРИМЕР 12.4. Определим J для данных примера 12.1 (вариант А). Напишем уравнение, в котором для сокращения записи при­мем 1 + J = г.

Исходная функция, определяющая чистый приведенный доход:

Л/(г) = -ЮОГ¹ - 150Г² + 50Г³ + 150Г⁴ + 200Г⁵ + 200Г⁶ = 0.

Решение заключается в определении корня шестой степени. Применим в методических целях способ последовательного под­бора, который представим в табл. 12.2.

Таблица 12.2

t	Я	15%	25%	30%
1	-100	-86,957	-80,000	-76,923
2	-150	-113,422	-96,000	-88,757
3	50	32,876	25,600	22,758
4	150	85.763	61,440	52,519
5	200	99,435	65,536	53,866
6	200	86,466	52,429	41,435
N		104,162	29,005	4,900

Возьмем в качестве исходной ставку, равную, допустим, 15%. Найдем величину чистого приведенного дохода по этой ставке: Л/(1,15) = 104,16, т.е. он заметно отличается от нуля. Принятое значение ставки явно мало. Изменяя величину ставки в нужном направлении, приближаемся к условию N(r) = 0. Повысим г до уровня 1,25. Получим N(1,25) = 29,0. Ноль в значении функции опять не достигнут. Далее находим Л/(1,3) = 4,9. Можно окончить расчет и удовлетвориться достигнутой точностью или продолжить его и еще раз увеличить ставку, скажем, до 31%. В этом случае N(1,31) = 0,8. Увеличивать точность расчета далее, вероятно, не имеет смысла.

Применим теперь программу ВНДОХ. Получим J = 0,3216. Со­ответственно, Л/( 1,3216) = 0,001.

В случае, когда инвестиции "мгновенны", а поток доходов может быть представлен в виде постоянной ренты, задача упро­щается и сводится к определению ставки / на основе знакомо­го нам равенства:

п\Г

К= R*

Из этой формулы следует

^an;J =

jK R

1 - (1 + J)ⁿ J

(12.12)

271

Таким образом, задача заключается в расчете искомой став­ки по заданному коэффициенту приведения постоянной ренты. Эта проблема обсуждалась в гл. 5.

ПРИМЕР 12.5. Инвестиции к началу срока отдачи составили 4 млрд руб. Доход ожидается на уровне 0,7 млрд руб в год, по­ступления — в течение 10 лет.

Если полагать, что поступления происходят равномерно в пре­делах года (их можно приурочить к серединам соответствующих лет), то коэффициент приведения ренты можно записать следую­щим образом:

a₁₀,,05 =-5^ = 5,7143,

что соответствует J = 13,1 %.

В свою очередь, если поток доходов непрерывен и постоя­нен, то внутренняя норма доходности, назовем ее непрерывной внутренней нормой и обозначим <7', находится на основе коэф­фициента приведения непрерывной ренты:

_ К 1 - ё-°'^я
а«*' RС

На величину внутренней нормы доходности влияют те же факторы, что и на чистый приведенный доход, а именно, раз­меры инвестиционных расходов и доходов и специфика их рас­пределений во времени. Однако влияние здесь обратное — все, что увеличивает N, сокращает значение У.

При использовании внутренней нормы доходности в качест­ве ориентира для выбора и принятии инвестиционного реше­ния следует иметь в виду, что:

• 
  данный параметр эффективности не учитывает масштабов проекта,
  
• 
  существует возможность (правда, редкая) в некоторых си­туациях получить неоднозначные оценки эффективности, а иногда они вовсе отсутствуют,
  
• 
  при отсутствии опыта расчета или необходимых программ получение соответствующих оценок может быть связано с некоторыми затруднениями.
  

Здесь уместно привести два дополнительных замечания, за­трагивающих как внутреннюю норму доходности, так и чистый

272

приведенный доход. Так, если инвестиционный проект охваты­вает ряд самостоятельных объектов, каждый из которых харак­теризуется определенными капитальными затратами и отдачами от них, то для этих составных частей можно определить част­ные показатели чистого приведенного дохода. Чистый приве­денный доход проекта в целом равен сумме частных показате­лей. Этого нельзя сказать о внутренней норме доходности.

Потребность в применении того или другого показателя свя­зана с различием в их содержании. Если речь идет о максими­зации массы дохода, то резонно выбор проекта основывать на чистом приведенном доходе (такой выбор, разумеется, не обес­печивает наиболее эффективное использование затраченных средств). При стремлении максимизировать относительную от­дачу ориентируются на внутреннюю норму доходности.