Е. М. Четыркин финансовая математика
 Скачать 4.63 Mb. Скачать 4.63 Mb.
|
|
§15.1. Сущность опциона, основные понятия В последнее десятилетие заметно усилилось внимание к так называемым производным финансовым инструментам (derivative securities). Термин "производный" связан с тем, что стоимость такого инструмента как бы привязывается к стоимости того или иного базового финансового инструмента (underlying securities) и становится по отношению к нему производной (не в математическом смысле) величиной. Среди производных инструментов наибольший интерес, вероятно, вызывают опционы. В России опционы пока не получили заметного распространения. Однако ознакомиться, хотя бы кратко, с данным инструментом представляется своевременным. Под опционом (options) понимают право, но не обязательство, купить/продать некоторые финансовые инструменты, акции или валюту по оговоренной цене при наступлении срока или до него. За получение этого права покупатель опциона (buyer, holder) при заключении контракта уплачивает продавцу (seller, writer) некоторую премию (premium). Последняя представляет собой рыночную цену опциона. Таким образом, само право в этой операции становится товаром. Различают опционы на право покупки (call option) и на право продажи (put option). Для сокращения записи, опцион на право покупки часто называют опцион ком, опцион на право продажи — опцион пут. Опцион, который может быть реализован только в оговоренный в контракте день, день исполнения (expiration day, day of maturity), называют европейским. Если предусматривается возможность исполнения опциона в любой момент до этого дня, то такой опцион называют американским. Заметим, что приведенные названия не определяют место сделки. Например, американский опцион может быть куплен и в Европе. Оговоренная в контракте цена объекта опциона называется объявленной, договорной ценой, или ценой исполнения (striking price, exercise price). 319 Опционы распространяются на акции, динамику их цен (stock index option), различные долговые обязательства, в том числе облигации, казначейские векселя, долговые сертификаты и другие подобного рода бумаги (option on debt instrument), курсы валют (option on currencies exchange rate), процентные ставки (interest rates option) и другие объекты. Существует особый класс так называемых экзотических опционов — на право покупки/продажи некоторых видов товаров (металлы, нефть) и даже на право обмена акций одного вида на акции другого вида. Каждый из перечисленных объектов опциона имеет свои особенности, которые должны учитываться в технике выполнения и методе анализа операции. Можно сказать, что опцион является особым случаем форвардной операции. Он отличается от форвардной операции прежде всего тем, что владелец опциона может реализовать свое право на сделку или отказаться от ее исполнения. Если сделка не исполняется (отказ от исполнения), то владелец опциона несет потери только в размере выплаченной им премии. Охарактеризуем опционы колл и пут с позиций как покупателя, так и продавца. Исполнение опциона может быть реализовано в нескольких вариантах. Рассмотрим их применительно к опциону колл при покупке акции. Если есть основание ожидать, что цена акций компании G будет расти (оптимистический прогноз) в течение некоторого периода, то инвестор может купить опцион колл. Пусть условия опциона таковы: цена исполнения 900, премия 50. Допустим в день исполнения рыночная цена акции оказалась равной 1050. Владелец опциона использует свое право и покупает их по цене исполнения, получая прибыль в размере 1050 - (900 + 50) = = 100 на одну акцию. Таким образом, опцион реализуется — приносит доход. Опцион может быть реализован и без непосредственной покупки акции — путем получения владельцем опциона разности между рыночной ценой акции и ценой исполнения. Если рыночная цена акции равна 950, то прибыль инвестора будет нулевая: 950 — (900 + 50) = 0. В этом случае для владельца опциона безразлично, купить ли акцию на рынке без опциона или использовать опцион. В обоих решениях его издержки одинаковы. Наконец, при цене ниже 950 покупатель отказывается от исполнения опциона и несет убытки. Максимальный убыток равен премии 50, размер прибыли не ограничен. 320 Приведенный пример иллюстрируется на графике "прибыль
Обратимся к положению продавца опциона колл в этой сделке. Очевидно, что прибыль/потери продавца опциона "симметричны" потерям/прибыли покупателя опциона: там, где у покупателя — доход, у продавца — потеря, и наоборот. Максимальная прибыль равна SO, размер убытка не ограничен. Если цена акции компании G превышает 950, то продавец несет убытки (см. рис. 15.2).
Прибыль покупателя i 100 о -50 Цена акции Цена акции Рис. 15.1 Прибыль п 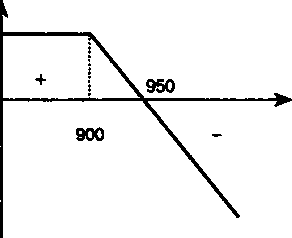 родавца родавцаi 50 0 Рис. 15.2 321 Перейдем к опционам пут (напомним, что это опцион на право продажи). Пусть ожидается падение цены акций компании G (пессимистический прогноз). В этой ситуации можно продать опцион колл. Однако, как только что было показано, позиция продавца оказывается довольно рискованной. Вместо этого он предпочитает купить опцион пут. Условия опциона: цена исполнения 870, премия 40. Картина зависимости "прибыль—цена акции" для покупателя опциона пут в этой ситуации кардинальным образом меняется. Если рыночная цена акции меньше 870 — 40 = 830, то покупатель опциона имеет прибыль. Например, при цене акции 810 прибыль составит 870 - (810 + 40) = 20. При цене 830 прибыль нулевая, так как 870 - (830 + 40) = 0, а при цене, превышающей 830, имеет место убыток, максимальная величина которого составляет 40. Прибыль/потери продавца такого опциона показаны на рис. 15.3. О -40 Цена акции П 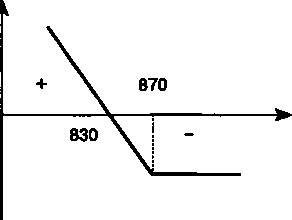 рибыль покупателя рибыль покупателяРис. 15.3 Цена акции 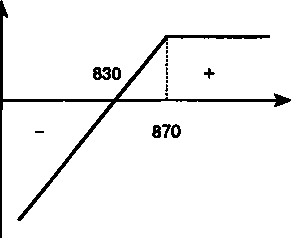 Прибыль продавца Прибыль продавца 40 О Рис. 15.4 322   Последствия действий продавца опциона для покупателя в зависимости от рыночной цены акции отражены на рис. 15.4. Последствия действий продавца опциона для покупателя в зависимости от рыночной цены акции отражены на рис. 15.4.Как было показано, положения покупателя и продавца опциона в отношении прибыли являются "зеркальными отображениями". Различаются они и по моменту получения ожидаемой прибыли. Продавец получает ее немедленно, покупатель — в момент реализации опциона. Приведем пример валютного опциона. Ограничимся при этом позицией покупателя опциона колл. ПРИМЕР 15.1. Импортер, который имеет швейцарские франки и в будущем должен выплатить некоторую сумму в долларах США, приобретает опцион на право покупки долларов по курсу 1 долл. США = 2,00 шв. франка и выплачивает премию 0,03 шв. фр. за 1 долл. При наступлении срока валютирования возможны следующие варианты завершения операции, определяемые движением курса доллара. 1. Курс доллара упал до 1,90 шв.фр. В этом случае покупатель не использует опцион и покупает доллары на рынке. Его резуль таты: — разность между курсом опциона и рыночным курсом слот: 2,00 - 1,90 = 0,10;
на 1 долл.: 0,07. 2. Курс доллара вырос до 2,15 шв.фр. Покупатель опциона ис пользует свое право на покупку валюты по цене исполнения (ого воренному курсу). Результат: реальная прибыль в размере 2,15 - - (2,00 + 0,03) = 0,12 шв.фр.на 1 долл.
- 2,02 = 0,01 на 1 долл. Приобретение права на покупку объекта опциона имеет смысл при ожидании повышения его цены. Право на продажу, очевидно, покупается при ожидании снижения цены. Как видно из приведенных рисунков, область изменения рыночной цены акции делится на два интервала, доходный (in the money) и бездоходный (out the money), разделяемые ценой исполнения сделки. Для опциона колл в доходном интервале ры- 323 ночная цена больше цены исполнения, их разность положительна (на рис. 15.1 интервал цен, превышающих 950). В бездоходном интервале разность рыночной цены и цены исполнения отрицательна. Наконец, при равенстве рыночной цены цене исполнения имеем так называемый нейтральный опцион (at the money). Аналогичные по содержанию интервалы можно выделить и при покупке опциона пут. Помимо простых схем опциона, которые были только что охарактеризованы, на практике прибегают и к более сложным, комбинированным схемам. Такие схемы предполагают одновременную покупку двух, трех опционов с различными характеристиками. Основное назначение комбинированных схем — гарантирование владельца опциона от значительных потерь. Например, одновременно покупается и продается опцион колл по разным ценам исполнения и с различными премиями, одновременно используются опционы пут и колл при одинаковой или различных ценах исполнения, двух опционов колл с различными ценами исполнения и одного опциона пут и т.д. Естественно, что чем больше простых опционов охватывает комбинированная схема, тем сложнее ее осуществить — труднее найти контрагентов по сделке. Приведем график формирования прибыли для комбинированной схемы, предусматривающей покупку опциона колл с низкой ценой исполнения Ехи продажу опциона колл с высокой ценой исполнения Е2(см. рис. 15.5). Прибыль/потери от комбинации опционов показана жирной линией, с, и с2 — стоимости опционов. 0 Цена акции П 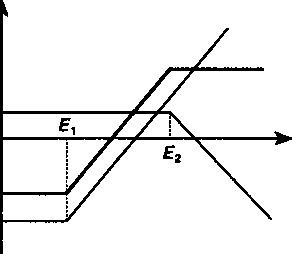 рибыль рибыльРис. 15.5 324 §15.2. Цена опциона Как было показано выше, реальные прибыль или потери от опциона для обеих участвующих сторон зависят от цены исполнения, рыночной цены актива на момент исполнения опциона, премии. В условиях развитого рынка опционов цена исполнения устанавливается на бирже опционов. Обычно это величина, близкая к текущей рыночной цене актива. Если биржа опционов отсутствует, то единственный путь установления цены исполнения — непосредственная договоренность покупателя и продавца опциона. Рыночные цены актива, на которые ориентируются стороны в опционной сделке, не реальные, а ожидаемые величины. Можно полагать, что чем больше они отклоняются от цены исполнения, тем меньше их вероятность. Если принять в качестве одной из возможных рабочих гипотез нормальное распределение этих вероятностей, то зависимость "вероятность—прибыль" для опциона колл на фафике выглядит таким образом (см. рис. 15.6), что цена исполнения £ является центром распределения вероятностей. С увеличением рыночной цены прибыль увеличивается, одновременно уменьшается вероятность этого события. В разработанных математических моделях для определения цены опциона, одна из которых кратко охарактеризована ниже, вместо нормального распределения обычно используется логарифмически нормальное (логнормальное) распределение, а центр распределения относят к цене исполнения. Иначе говоря, предполагается, что распределение вероятностей для ожидаемых рыночных цен является асимметричным (вершина сдвинута влево). Таким образом, предусматривается, что вероятность получения прибыли выше, чем потерь. Наиболее интересным среди перечисленных факторов является премия (цена опциона). Выше отмечалось, что цена опци- Цена акции 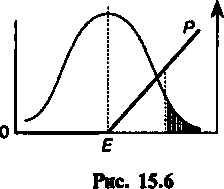 Прибыль* Прибыль* Вероятность реализации 325 она складывается на рынке. Предлагаемая продавцом цена должна быть конкурентоспособной и в то же время обеспечить ему некоторую прибыль. К проблеме формирования цены можно подойти аналитически. Прежде всего можно определить "естественные" границы этой цены. Так, в первом приближении для европейского опциона колл минимальная цена равна нулю, максимальная — цене акции, так как право на покупку вряд ли может превышать цену самой акции. Таким образом, О < с < 5, где с — цена опциона, S — текущая цена акции. В то же время цена опциона к моменту истечения срока равна разности ожидаемой рыночной цены и цены исполнения: c=S-E.(15.1) Верхние и нижние границы опциона колл показаны на рис. 15.7. Для того чтобы уточнить границы значений цены опциона, а также лучше представить себе свойства опциона и фигурирующих в нем показателей, сравним расходы на приобретение акции непосредственно на рынке (стратегия А) и при покупке опциона колл (стратегия Б). Пусть срок опциона и приобретения акции — один год, цена акции равна S, цена исполнения Е. Возможные стратегии покупателя и их финансовые последствия представлены в табл. 15.1. В графе "Расходы" этой таблицы показаны стоимостные показатели на день исполнения опциона, в графе "Инвестиции" — его расходы на день покупки опциона. Опцион при условии S < Ене реализуется, акции мо- Цвна опционаа 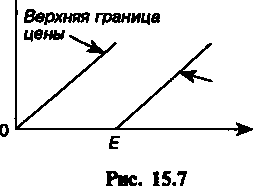 Нижняя граница цены Цена акции 326 гут быть куплены на рынке (стратегия А). Если S > Е, то следует применить стратегию Б. Премия для альтернативной ситуации определена в размере с = S — Е. Величина Ev означает современную стоимость цены исполнения на день покупки опциона, v — дисконтный множитель. Расходы на приобретение акции во всех ситуациях равны S. Таблица 15.1
Теперь становится очевидным, что вместо (15.1) следует использовать с = S- PV(E) = S- Svy(15.2) где ЯК— оператор определения современной стоимости на момент выплаты премии, v — дисконтный множитель по рыночной процентной ставке. Аналогичным образом получим ограничение для цены опциона пут: с = PV(E) - S. Приведенные выше выражения позволяют получить значения премии для нескольких величин цены акции. Так, если ожидаемая цена акции минимальна, то премия опциона колл, естественно, нулевая. Для ситуации, когда S = Е, получим максимальную величину премии: с = Е - PV(E). | |||||||||||||||||||||||||||||||||||||||||
