Е. М. Четыркин финансовая математика

• Название: Е. М. Четыркин финансовая математика
• Анкор: chetyrkin_e_m_finansovaya_matematika.doc
• Дата: 22.04.2017
• Размер: 4.63 Mb.
• Имя файла: chetyrkin_e_m_finansovaya_matematika.doc
• Тип: Учебник; #4971
• страница: 27 из 58

§17.1. Нетто-премии в личном страховании

Страхование на дожитие. Для начала рассмотрим самый про­стой, но очень важный в методическом плане случай личного страхования — страхование на дожитие (pure endowment). Итак, человек в возрасте х лет договаривается со страховой организа­цией о том, что при достижении им, допустим, 60 лет он полу­чит S рублей. Для определения размера премии найдем матема­тическое ожидание суммы страховой выплаты, дисконтирован­ной на срок страхования, т.е. на 60 — х лет. Размер нетто-пре­мии данного вида страхования обозначим как _пЕ_х. Для рассма­триваемого примера:

60-А ⁼ во-хРх * ^v6°* * £

где м-хРх — вероятность лицу в возрасте х лет дожить до 60 лет, v⁶⁰"* — дисконтный множитель по принятой ставке сложных процентов.

В общем виде с использованием коммутационной функции D_xполучим

A-A*»-*$-^'«S--^^-xJ-^S<17.1)

Влияние принятой процентной ставки здесь очевидно. Чем она выше, тем меньше страховая премия.

ПРИМЕР 17.1. Необходимо найти стоимость страхования на до­житие до 60 лет мужчины в возрасте 40 лет. Если расчет основы­вать на процентной ставке, равной 9%, то согласно (17.1) полу­чим<sup>1

1</sup> Значения коммутационных чисел, приведенные в примерах, взяты из табл. 12 Приложения.

349

^Deo389,17

20^е* = IT'S = ' _c S = 0,13239 S.
^{20 x} Одо 2939,5

Премия здесь составляет чуть больше 13% страховой суммы. Полученная величина представляет собой нетто-ставку страхова­ния на дожитие, т.е. ставку, определенную из условия эквивалент­ности обязательств страхователя и страховщика. Напомним, что она не учитывает расходов страховщика на ведение дела.

Для того чтобы лучше понять смысл полученных результа­тов, предположим, что число застрахованных на дожитие в при­мере 17.1 равно 1000 человек, а страховая сумма равна 1 тыс. руб. Таким образом:

число застрахованных 1000

премия от одного застрахованного 132,39 руб.

общая сумма премии 132 390 руб.

сумма с процентами за 20 лет 741 968 руб.

количество лиц, доживших до 60 лет 742 (точно 741,968)

общая сумма выплат 742 000 тыс. руб.

Как видим, наблюдается полная сбалансированность между взносами и выплатами, демонстрирующая соблюдение принци­па эквивалентности обязательств страхователей и страховщика (небольшая разница объясняется округлением числа доживших).

Приведенный пример иллюстрирует действие принципа со-лидарной ответственности страхователей — важнейшего стра­хового принципа. Дело в том, что страхователь, доживший до 60 лет, часть денег получил за счет тех лиц, которые не дожили до обусловленного возраста (согласно таблице смертности та­ких окажется в среднем 258 человек из тысячи застрахованных). Если оговоренную сумму он обеспечивает самостоятельно, без солидарной ответственности всех участников, то ему необходи­мо было бы внести на сберегательный счет 178,43 руб., а не 132,39 руб.

Страхование супружеской пары. Выше постановка задачи лич­ного страхования обсуждалась применительно к отдельному че­ловеку. Распространим теперь методику страхования на супру­жескую пару, при этом ограничимся страхованием на дожитие.

Пусть речь идет о супружеской паре, имеющей возраст х и у лет. Страховым событием здесь является дожитие до возрастов х+яиу+й или дожитие одного из супругов до оговоренного

350

возраста. В первом варианте нетто-премия в расчете на один рубль страховой суммы определяется как

Лу = пРх * пРу * V^я = -ТрЧ (17.2)

^иху

где _пр_хи _пр_у— вероятности прожить еще п лет для каждого из супругов, D_YV— коммутационная функция (см.(16.14) и (16.15)).

Во втором варианте страховая сумма выплачивается одному из супругов, например вдове, при условии, что она проживет до у + п лет. Получим следующую величину нетто-премии:

Л\у - пР_Х\у * V" = ^" "^f⁴"' ^(,7-³⁾

У ХУ

где _пр_х^ — вероятность того, что супруг (заключивший договор в х лет, когда его супруге было у лет) не доживет до возраста х + п, а супруга, напротив, доживет до у + п лет (см. (16.7)).

Величину _яЯф можно рассчитать с помощью коммутацион­ных чисел. Обратимся к первой дроби в правой части равенст­ва (17.3). Умножим и разделим ее на v>\ Получим знакомое вы­ражение для нетто-премии на дожитие (17.1). Что касается вто­рой дроби, то для ее определения необходимы другие коммута­ционные числа (см. (16.14) и (16.15)).

Вернемся к формуле (17.3). Умножим и разделим вторую дробь на v^yV¹. После чего получим

»^Е4у DD '⁽ '

У ху

Искомая величина равна разности нетто-премий страхова­ния на дожитие супруги и страхования на дожитие супружеской пары.

ПРИМЕР 17.2. Определим размер нетто-премии страхования на 5 лет на дожитие супругов. Для супружеской пары (х = 50, у = = 45 лет) находим следующие коммутационные числа при усло­вии, что процентная ставка равна 9% (первая строка — для муж­чин, вторая — для женщин):

D* = 050 = ¹¹²⁴'⁸; ^Dx+n = 0₅₅ = 673,1;

351

Dy = 045=1991,9; Dy+n = D	so = 1268,8;
(x + y)/2 = (50 + 45) / 2	= 47,5.
Отсюда
°xy = D50; 45 = 10"3 * 1124>8 * 1991 -9 :	к1,09475 = 134 799;
*V„ = 055; я, = Ю-3 ж 673,1 ж 1268,8 ,	< 1,095+475 = 78 770.
При страховании на дожитие супружеской пары получим
ЕтЕ. 78770 ш rFxy 5С50;45 134 799	0,58435.
При страховании на дожитие вдовы:
1268,8 78 770 \ Е, = *£=„,« = ! = 0,63698 - 0,58435 - 0,05263. лсх|у 5С50|45 1991,9 134 799 ",wus,° u,JOW '

§17.2. Страхование жизни

Этот вид страхования (life insurance), называемый также стра­хованием на случай смерти, является наиболее распространен­ным. Страховая сумма, равная 5, выплачивается в случае смер­ти застрахованного. Допустим, страховой договор заключается в возрасте х лет. Если смерть наступит на первом году страхо­вания, а выплата страховых сумм наследникам производится в конце года наступления страхового события, то с учетом веро­ятности этого события современная величина выплаты (на мо­мент заключения контракта) составит q_x(Sv); если страховой случай наступит во втором году, то аналогичная по содержанию величина равна ₂Я_Х(^) ^{и Т}-Д-

Единовременную нетто-премию определим исходя из прин­ципа эквивалентности обязательств. Искомая величина равна современной стоимости страхового аннуитета или математиче­скому ожиданию суммы дисконтированных выплат. Поскольку необходимые значения вероятностей находятся на основе таб­лицы смертности как d_x/l_x(см. § 16.2), то искомая величина премии при условии, что страхование пожизненное, определя­ется как

352

A=-rvS+ -^-v²^ + ... + -7- v«-^xS.

Умножим и разделим каждое слагаемое на V^хи используем коммутационную функцию D_x. После чего получим

A=S

*x+\ + —^±i-_vx+2 ₊ + _% o>

D„ D„ D

X

\ x **x **x

Применив коммутационную функцию М_х(см. (16.13)), окон­чательно имеем

Л/
A_x--f&07.5)

X

Пожизненное страхование жизни встречается не так уж час­то. Обычно практикуют страхование на срок. Пусть этот срок равен п годам. Нетто-премия в этом случае составит

Л/. А/„._

л ——r^^s-<^l7-⁶>

ПРИМЕР 17.3. Найдем величину премии в виде доли от страхо­вой суммы для сорокалетнего мужчины при пожизненном страхо­вании жизни:

Мдо 431,4

^A^^ ⁼ ^^s=-i^iJ^s=0-^14678S-

Для варианта с ограничением срока страхования двадцатью годами получим:

^М40^М60 431,4-134,7
Их - «Л* - %^S _iiiiJ-S = 0.10094S.

Как видим, ограничение срока заметно снизило стоимость страхования.

На практике часто премии выплачиваются в рассрочку. Пос­леднее равносильно замене разовой выплаты премии постоян­ной рентой. Пусть рассрочка осуществляется посредством пла­тежей пренумерандо в течение / лет. Условие равенства обяза­тельств сторон в страховании запишем следующим образом:

353

М_х— М_х+п

где R — член страхового аннуитета (размер ежегодной премии), а^л — стоимость немедленного ограниченного страхового анну­итета (см. (16.22)).

После несложных преобразований имеем

A/_v Л/.
* = s-N^&(17J)

ПРИМЕР 17.4. Допустим, единовременный взнос в примере 17.3 (пожизненное страхование) заменяется на выплаты в рассрочку в течение 20 лет. В этом случае

Чю 431,4
R = ——S = ■ S = 0,01581 S.

^NA0'^N60³⁰³⁷⁶ " ³⁰⁸²

Смешанное страхование. Нетрудно объединить страхование на дожитие и на случай смерти. Если страховое возмещение обоих рисков одинаково, то в расчете на один рубль страховой суммы получим следующую сумму единовременной нетто-пре-мии:

А + Л п * 07-8)

X

Для рассрочки платежей в течение / лет получим

D+ М- М_х+п
*- _N-_N^s-(>⁷-9)

^1Ух ⁿx+t

§17.3. Пенсионное страхование. Виды пенсионных схем

Проблема пенсионного обеспечения затронула в последнее десятилетие все развитые страны, что в значительной мере свя­зано с заметным старением населения. Не избежала этой проб­лемы и Россия. Свой вклад в ее решение вносят негосударст­венные пенсионные фонды (НПФ). Пенсионные фонды не но-

354

вость для России. До 1917 г. подобного рода учреждения функ­ционировали в стране под названием пенсионные и эмериталь­ные кассы.

С экономической точки зрения обеспечение пенсиями по старости на базе НПФ представляет собой своеобразный дол­госрочный инвестиционный процесс, на первом этапе кото­рого осуществляются вложения (взносы в фонд) и последова­тельное наращение средств за счет доходов от инвестиций свободных денежных средств, на втором -— получение отдачи от накоплений в виде периодических пенсий. Особенности данного процесса определяются принятыми правилами, рег­ламентирующими взносы и выплаты пенсий (пенсионные схемы).

В длительно действующих пенсионных фондах скаплива­ются громадные средства. Например, активы пенсионных фондов стран Европейского союза в 1993 г. составляли более 1,2 трлн долл.

По условиям финансирования пенсионные схемы, практикуе­мые в России, подразделяются на:

— нефондируемые (предусматривается выплата пенсий из те­
кущих поступлений); эти схемы не представляют большо­
го интереса в отношении применения количественного
финансового анализа;

-— фондируемые, или накопительные, (для обеспечения вы­плат пенсий создаются целевые фонды);

— частично фондируемые (целевые фонды создаются не для
всех участников; например, только для лиц, выходящих
на пенсию).

К фондируемым схемам относятся:

• 
  сберегательные (отличительные особенности: не учитыва­ются вероятности дожития каждого участника фонда, пре­дусматривается наследование накоплений, отсутствует со­лидарность участников в обеспечении выплат, оговарива­ется конкретный срок выплат); данный метод обеспече­ния старости представляет собой покупку индивидуаль­ной финансовой ренты;
  
• 
  страховые (солидарность участников, нет наследования накоплений, учитываются вероятности дожития застрахо­ванных);
  

355

— смешанные сберегательно-страховые схемы (предусматри­
вается последовательное использование двух схем, напри­
мер, на этапе накопления применяется сберегательная
схема, на этапе выплат пенсий — страховая).

Страховые схемы различаются по охвату участников фонда:

• 
  индивидуальные схемы, в которых пенсии эквивалентны индивидуальным накоплениям для каждого участника,
  
• 
  групповые схемы, в которых пенсии и накопления экви­валентны для всех участников фонда "в массе".
  

Сбалансированность взносов и выплат (иначе говоря, экви­валентность обязательств) — необходимое условие для нор­мального ведения дела и важный элемент гарантии выполнения обязательств НПФ по выплатам пенсий. В страховых схемах ба­ланс обеспечивается на основе применения страховых принци­пов, которые реализуются с помощью актуарных расчетов. В сберегательных схемах баланс достигается на основе теории верных финансовых рент.

При применении любой из пенсионных схем с фондирова­нием сталкиваются с необходимостью решения двух задач. Пер­вая выступает в двух "сопряженных" вариантах: определение размера пенсии по величине установленных взносов либо рас­чет величины взносов по заданным размерам пенсии.

Вторая задача заключается в расчете страховых резервов. В следующих параграфах главы обсуждаются обе задачи.

§17.4. Расчет премий и пенсий. Сберегательные схемы

В российских НПФ получили распространение как страхо­вые, так и сберегательные пенсионные схемы. В методических целях анализ удобнее начать с последних. В таких схемах пла­тежи (взносы и пенсии) не увязываются с вероятностями их вы­плат, поэтому нет необходимости применять таблицы смертно­сти и коммутационные числа, где аргументом является возраст. Строго говоря, здесь, по-видимому, нет оснований и для при­менения терминов "премия" и "пенсия". Однако для единооб­разия сохраним эти термины и в сберегательных схемах обеспе­чения старости.

Для расчета премий, очевидно, следует применять формулы, определяющие современные стоимости рент, если премия вы-

356

плачивается единовременным взносом, или размеры членов ог­раниченных, постоянных рент, если премии выплачиваются в рассрочку. Соответствующие методы были подробно обсужде­ны в гл. 5, поэтому ограничимся примером, в котором пенсия выплачивается в виде годовой, ограниченной ренты пренуме-рандо. Рассмотрим методы расчета суммы единовременного взноса и размеров последовательных взносов в фонд в течение ряда лет. Для записи формул примем следующие обозначения:

R — годовая сумма пенсии, Е — размер единовременного взноса,

А — сумма, накопленная на индивидуальном счете участни­ка фонда на начало выплат пенсии, х — возраст застрахованного в момент заключения договора, L — возраст выхода на пенсию, w — возраст в момент окончания действия контракта, п — срок накопления, п = L - х, / — срок выплат пенсии, / = w - L.

Как показано на рис. 17.1, общий срок делится на два пери­ода. В первом — в возрасте от л: до L лет — взнос в сумме Е (здесь и далее речь идет о "чистых" взносах, аналогах нетто-премии в страховых схемах) увеличится до величины А. Эта сумма обеспечивает оговоренные выплаты до возраста w во вто­ром периоде.

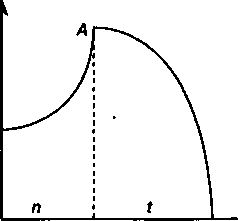
Накопления

Е

х L w Возраст

Рис 17.1

ПРИМЕР 17.5. Определим размеры премий, необходимые для обеспечения выплат страховой пенсии. Пенсионные выплаты, от­ложенные на 20 лет, должны производиться в размере 10 тыс. руб. в год, пренумерандо. Срок выплат f = 15 лет.

357

Таким образом, выплаты представляют собой отложенную на 20 лет, ограниченную годовую финансовую ренту, член которой равен 10 тыс. руб. Очевидно, что единовременный взнос равен современной стоимости будущих выплат. Положим, что на взнос начисляются проценты по ставке / = 9%. Общая формула для рас­чета имеет вид

Е= Ах vⁿ= R хa_t; i x (1 + i)vⁿ_t

где v — дисконтный множитель по ставке /, а_п;,(1 + /) — коэффи­циент приведения постоянной ренты пренумерандо (см. § 5.3),

4 = 10 000а_{15; 9} х 1,09 = 10 000 х 8,060688 х 1,09 = 87 861 руб.,

Е= 87 861 х 1,09-2° = 15 677 руб.

Динамика пенсионных накоплений схематично показана на рис. 17.2.

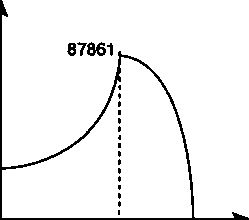
Накопления

15677

40 60 75 " Возраст

Рис. 17.2

Если страховой договор предусматривает рассрочку взносов (равными платежами) в течение m лет (п * л?), то необходимый размер ежегодного взноса пренумерандо легко получить на осно­ве следующего равенства:

Rti . = Avⁿ.

^пго; i ™*

Как показано выше, Avⁿ= 15 677,

*10; 9 ^{= а}10; 9 ^х <^{1 +} '> ⁼ 6,41766 х 1,09 = 6,99525.

Окончательно имеем

15 677

*=^i^- ^{= 2241}'^1py6-

358

Таким образом, имеется альтернатива — выплатить единовре­менно 15,7 тыс. руб. или ежегодно на протяжении 10 лет по 2,2 тыс. руб.

Короткое замечание об учете инфляции. Безусловно этот фа­ктор должен быть учтен при определении размера пенсии вне зависимости от выбранной схемы. За рубежом обычно (при низких темпах инфляции) для этого увеличивают применяемую в расчетах процентную ставку на величину ожидаемого долго­срочного темпа инфляции. При большом темпе такой прием невозможен. Единственный разумный путь — периодическая корректировка пенсии с учетом реально полученного дохода от инвестирования накоплений.