|
|
Физике. физика. Электродинамика Электрические токи в металлах, вакууме и газах. Электрический ток в жидкостях
Фоторезисторы. Принцип действия фоторезисторов – фотоэлектрических полупроводниковых приемников излучения, основан на фоторезистивном эффекте. Фоторезисторы находят применение в устройствах коммутации электрических цепей, а также в различных ключевых и аналоговых устройствах систем автоматического управления, контроля и регулирования различных физических величин.
 Устройство фоторезистора показано на рис. 5.11. Светочувствительный элемент фоторезистора представляет собой прямоугольную или круглую таблетку, спрессованную из полупроводникового материала, или тонкую пленку 1 на стеклянной, слюдяной или керамической подложке 2. На концах светочувствительного элемента создают электроды 3 с малым сопротивлением. Устройство фоторезистора показано на рис. 5.11. Светочувствительный элемент фоторезистора представляет собой прямоугольную или круглую таблетку, спрессованную из полупроводникового материала, или тонкую пленку 1 на стеклянной, слюдяной или керамической подложке 2. На концах светочувствительного элемента создают электроды 3 с малым сопротивлением.
Наиболее распространенными являются фоторезисторы на основе сернистого свинца (PbS), cеленистого свинца (PbSe), сернистого кадмия (CdS) и селенистого кадмия (CdSe). Высокая фоточувствительность сульфида и селенида кадмия обеспечивается введением в их состав сенсибилизирующих примесей, способствующих увеличению времени жизни основных носителей заряда. Донорной примесью обычно служит хлор, в качестве акцепторных примесей используются медь или серебро. Существенную роль в механизме проводимости играют также структурные дефекты.
Сернисто-свинцовые и селенисто-свинцовые фоторезисторы изготавливают нанесением на изоляционное основание тонкого полупроводникового слоя путем испарения в вакууме или химического осаждения. Селенисто-кадмиевые и сернисто-кадмиевые фоторезисторы в большинстве случаев выполняют из порошков CdSе и CdS путем прессования в виде таблеток, которые далее подвергают термической обработке и затем приклеивают к изоляционному основанию, на которое с целью создания контактов нанесены металлические электроды. В качестве светочувствительных элементов для изготовления фоторезисторов используют также монокристаллы CdSе и CdS. Монокристаллические образцы размером мм укрепляют на изолирующей подложке специальными лаками. Для создания омических контактов на края кристаллов наносят металлические электроды.
Вольтамперные характеристики фоторезистора без освещения и при освещении относительно небольшим световым потоком Ф почти линейны, их графики приведены на рис. 5.12, а.
Зависимость электросопротивления фоторезистора R = f(Ф) от величины светового потока Ф (функциональная характеристика) аппроксимируется приближенным соотношением вида
R
Ф–1/2 (рис. 5.12, б). Темновое сопротивлениефоторезистора при полной защите чувствительного элемента от излучения составляет (0,022¼100)×106 Ом.
Отношение Rт/Rсв темнового сопротивления Rт фоторезистора к световому сопротивлению Rсв измеренному при освещенности в 200 лк, для различных типов фоторезисторов на основе CdS и CdSe колеблется в широком диапазоне от 3,5 до 1,5×106 (обычно 150...1500), для фоторезисторов на основе PbS значение Rт/Rсв постоянно и равно 1,2 отн. ед.
Инерционность фоторезисторов определяется процессами релаксации фотопроводимости, контролирующими крутизну фронтов нарастания и спада фотопроводимости. Например, у приборов на основе CdS уменьшение чувствительности заметно уже на частоте около 100 Гц, а на основе PbS – на частоте более 1 кГц. Это означает, что инерционность фоторезисторов – величина порядка единиц мс.

В зависимости от типа используемого фоточувствительного материала фоторезисторы имеют различные спектральные характеристики, изображенные на рис. 5.12, в. Так, сернисто-кадмиевые и селенисто-кадмиевые фоторезисторы характеризуются максимумом чувствительности в видимой области спектра (l = 0,6 мкм и 0,8 мкм, соответственно). Фоторезисторы, выполняемые из сульфида свинца и селенида свинца имеют максимум спектральной чувствительности в инфракрасной области спектра (l = 1,8 мкм и 3,5 мкм, соответственно). Максимальную длину волны, при которой наблюдается внутренний фотоэффект, называют красной границей.
Область спектральной зоны чувствительности фоторезистора можно расширить на всю видимую часть спектра от 0,4 до 0,9 мкм, используя материалы на основе твердых растворов между CdS, CdSe, CdTe, например CdSe-CdTe.
Спектральные характеристики поликристаллических фоторезисторов, вследствие повышеной концентрации примесей в них, шире, чем монокристаллических, они растянуты за пределы границы собственного поглощения в область коротких длин волн (рис. 5.12, в).
Фоторезисторы являются составной частью оптико-электронного устройства – резисторного оптрона (оптопары). При этом фоторезистор и источник излучения заключены в общий светонепроницаемый корпус и находятся в оптической связи друг с другом. В качестве источника излучения применяют миниатюрные лампы накаливания, светодиоды, электролюминесцентные излучатели.
Эффе́кт Хо́лла — явление возникновения поперечной разности потенциалов (называемой также холловским напряжением) при помещении проводника с постоянным током в магнитное поле. Открыт Эдвином Холлом в 1879 году в тонких пластинках золота.
В простейшем рассмотрении эффект Холла выглядит следующим образом. Пусть через проводящий брусок в слабом магнитном поле течёт электрический ток под действием напряжённости . Магнитное поле будет отклонять носители заряда к одной из граней бруса от их движения вдоль или против электрического поля. При этом критерием малости будет служить условие, что при этом носители заряда не начнут двигаться по циклоиде.
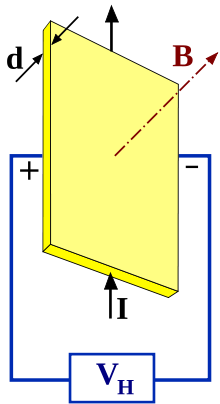
Таким образом, сила Лоренца приведёт к накоплению отрицательного заряда возле одной грани бруска, и положительного — возле противоположной. Накопление заряда будет продолжаться до тех пор, пока возникшее электрическое поле зарядов не скомпенсирует магнитную составляющую силы Лоренца:
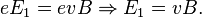
Скорость электронов можно выразить через плотность тока:
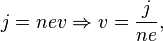
где — концентрация носителей заряда. Тогда
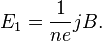
Коэффициент пропорциональности между и называется коэффициентом (или константой) Холла. В таком приближении знак постоянной Холла зависит от знака носителей заряда, что позволяет определять их тип для большого числа металлов. Для некоторых металлов (например, таких, как свинец, цинк, железо, кобальт, вольфрам), в сильных полях наблюдается положительный знак , что объясняется в полуклассической и квантовой теориях твёрдого тела.
5.Экспериментальное подтверждение квантовых свойств света.
Уравнение Эйнштейна для внешнего фотоэффекта.
А. Эйнштейн в 1905 г. показал, что явление фотоэффекта и его закономерности могут быть объяснены на основе предложенной им квантовой теории фотоэффекта. Согласно Эйнштейну, свет частотой v не только испускается, как это предполагал Планк, но и распространяется в пространстве и поглощается веществом отдельными порциями (квантами), энергия которых εo=hv. Таким образом, распространение света нужно рассматривать не как непрерывный волновой процесс, а как поток локализованных в пространстве дискретных световых квантов, движущихся со скоростью с распространения света в вакууме. Кванты электромагнитного излучения получили название фотонов.
По Эйнштейну, каждый квант поглощается только одним электроном. Поэтому число вырванных фотоэлектронов должно быть пропорционально интенсивности света (I закон фотоэффекта). Безынерционность фотоэффекта объясняется тем, что передача энергии при столкновении фотона с электроном происходит почти мгновенно.
Энергия падающего фотона расходуется на совершение электроном paботы выхода А из металла и на сообщение вылетевшему фотоэлектрону кинетической энергии mυ2max/2. По закону сохранения энергии,
hυ=A+mυ2max/2 (2.1)
Уравнение (2.1) называется уравнением Эйнштейна для внешнего фотоэффекта.
Уравнение Эйнштейна позволяет объяснить II и III законы фотоэффекта. Из (2.1) непосредственно следует, что максимальная кинетическая энергия фотоэлектрона линейно возрастает с увеличением частоты падающего излучения и не зависит от его интенсивности (числа фотонов), так как ни А, ни v от интенсивности света не зависят (II закон фотоэффекта). Так как с уменьшением частоты света кинетическая энергия фотоэлектронов уменьшается (для данного металла А = const), то при некоторой достаточно малой частоте υ=υ0 кинетическая энергия фотоэлектронов станет равной нулю и фотоэффект прекратится (III закон фотоэффекта). Согласно изложенному, уравнением Эйнштейна для внешнего фотоэффекта (2.1) получим, что
υ0=A/h (2.2)
и есть красная граница фотоэффекта для данного металла. Она зависит лишь от работы выхода электрона, т. е. от химической природы вещества и состояния его поверхности.
Выражение (2.1) можно записать, используя (1.1) и (2.2), в виде
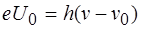
Уравнение Эйнштейна было подтверждено опытами Милликена. В его приборе (1916г.) поверхность исследуемого металла подвергалась очистке в вакууме. Исследовалась зависимость максимальной кинетической энергии фотоэлектронов, изменялось задерживающее напряжение U0(см. (1.1)) от частоты v и определялась постоянная Планка. В 1926 г. российские физики П. И. Лукирский (1894—1954) и С.С. Прилежаев для исследования фотоэффекта применили метод вакуумного сферического конденсатора.Анодом в их установке служили посеребренные стенки стеклянного сферического баллона, а катодом — шарик (R≈1,5 см) из исследуемого металла, помещенный в центр сферы. В остальном схема принципиально не отличается от описанной на рис.1. Такая форма электродов позволила увеличить наклон вольт-амперных характеристик и тем самым более точно определять задерживающее напряжение U0 (а следовательно, и h). Значение h, полученное из данных опытов, согласуется со значениями, найденными другими методами (по излучению черного тела и по коротковолновой границе сплошного рентгеновского спектра ). Все эго является доказательством правильности уравнения Эйнштейна, а вместе с тем и его квантовой теории фотоэффекта.
Если интенсивность света очень большая, то возможен многофотонный (нелинейный) фотоэффект,при котором электрон, испускаемый металлом может одновременно получить энергию не от одного, а от N фотонов (N=2÷7).
6. Фотоны. Масса и импульс фотона. Давление света.
Согласно гипотезе световых квантов Эйнштейна, свет испускается, поглощается и распространяется дискретными порциями (квантами), названными фотонами. Энергия фотонa ξ0=hv. Его масса находится из закона взаимосвязи массы и энергии :
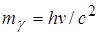 (4.1) (4.1)
Фотон— элементарная частица, которая всегда (в любой среде!) движется со скоростью света с и имеет массу покоя, равную нулю. Следовательно, масса фотона отличается от массы таких элементарных частиц, как электрон, протон и нейтрон, которые обладают отличной от нуля массой покоя и могут находиться в состоянии покоя.
Импульс фотона pvполучим, если в общей формуле теории относительности IM массу покоя фотона m0γ= 0:
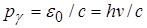 (4.2) (4.2)
Из приведенных рассуждений следует, что фотон, как и любая другая частица, характеризуется энергией, массой и импульсом. Выражения (205.1), (205.2) и (200.2) связывают корпускулярные характеристики фотона — массу, импульс и энергию волновой характеристикой света — его частотой v.
Если фотоны обладают импульсом, то свет, падающий на тело, должен создавать на него давление. Согласно квантовой теории, давление света на поверхность обусловлено тем, что каждый фотон при соударении с поверхностью передает ей свой импульс.
Рассчитаем с точки зрения квантовой теории световое давление, оказываемое на поверхность тела потоком монохроматического излучения (частота v), падающего перпендикулярно поверхности. Если в единицу времени на единицу площади поверхности тела падает N фотонов, то при коэффициенте отражения р света от поверхности тела pN фотонов отразится, а (1—р) N—поглотится. Каждый поглощенный фотон передает поверхности импульс pY=hv/c, а каждый отраженный — 2py=2hv/c (при отражении импульс фотона изменяется на — ру). Давление света на поверхность равно импульсу, который передают поверхности в 1 с N фотонов:
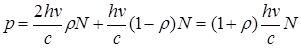
Nhv = Eeесть энергия всех фотонов, падающих на единицу поверхности в единицу времени, т. е, энергетическая освещенность поверхности, a Ee/c=w объемная плотность энергии излучения. Поэтому давление, производимое светом при нормальном падении на поверхность,
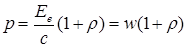 (4.3) (4.3)
Формула (4.3), выведенная на основе квантовых представлений, совпадает с выражением, получаемым из электромагнитной (волновой) теории Максвелла. Таким образом, давление света одинаково успешно объясняется и волновой, и квантовой теорией. Как уже говорилось, экспериментальное доказательство существования светового давления на твердые тела и газы дано в опытах П. Н. Лебедева, сыгравших в свое время большую роль в утверждении теории Максвелла. Лебедев использовал легкий подвес на тонкой нити, по краям которого прикреплены легкие крылышки, одни из которых зачернены, а поверхности других зеркальные. Для исключения конвекции и радиометрического эффекта использовалась подвижная система зеркал, позволяющая направлять свет на обе поверхности крылышек, подвес помещался в откачанный баллон, крылышки подбирались очень тонкими (чтобы температура обеих поверхностей была одинакова). Световое давление на крылышки определялось по углу закручивания нити подвеса и совпадало с теоретически рассчитанным. В частности оказалось, что давление света на зеркальную поверхность вдвое больше, чем на зачерненную (см. (4.3)).
7.Эффект Комптона и его элементарная теория.
Наиболее полно корпускулярные свойства света проявляются в эффекте Комптона. Американский физик А. Комптон (1892—1962), исследуя в 1923 г. рассеяние монохроматического рентгеновского излучения веществами с легкими атомами (парафин, бор), обнаружил, что в составе рассеянного излучения наряду с излучением первоначальной длины волны наблюдается также более длинноволновое излучение. Опыты показали, что разность ∆λ=λ’-λне зависит от длины волны λ падающего излучения и природы рассеивающего вещества, а определяется только углом рассеяния θ:
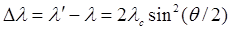 (5.1) (5.1)
λ’ - длина волны рассеянного излучения, λс -комптоновская длина волны.
Эффектом Комптонаназывается упругое рассеяние коротковолнового электромагнитного излучения (рентгеновского и γ-излучений) на свободных (или слабосвязанных) электронах вещества, сопровождающееся увеличением длины волны. Этот эффект не укладывается в рамки волновой теории, согласно которой длина волны при рассеянии изменяться не должна: под действием периодического поля световой волны электрон колеблется с частотой поля и поэтому излучает рассеянные волны той же частоты.
Объяснение эффекта Комптона дано на основе квантовых представлений о природе света. Если считать, как это делает квантовая теория, что излучение имеет корпускулярную природу, т. е. представляет собой поток фотонов, то эффект Комптона — результат упругого столкновения рентгеновских фотонов со свободными электронами вещества (для легких атомов электроны слабо связаны с ядрами атомов, поэтому их можно считать свободными). В процессе этого столкновения фотон передает электрону часть своих энергии и импульса в соответствии с законами их сохранения.
Рассмотрим упругое столкновение двух частиц (рис. 4)— налетающего фотона, обладающего импульсом pγ=hv/cи энергией ξγ=hv, спокоящимся свободным электроном (энергия покоя W0=m0c2; m0— масса покоя электрона). Фотон, столкнувшись с электроном, передает ему часть своей энергии и импульса и изменяет направление движения (рассеивается). Уменьшение энергии фотона означает увеличение длины волны рассеянного излучения. При каждом столкновении выполняются законы сохранения энергии и импульса. Согласно закону сохранения энергии,
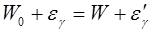 (5.2) (5.2)
а согласно закону сохранения импульса,
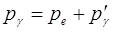 (5.3) (5.3)
гдe W0=m0c2 – энергия электрона до столкновения, ξγ=hv — энергия налетающего фотона, 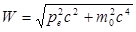 — энергия электрона после столкновения (используется релятивистская формула, так как скорость электрона отдачи в общем случае значительна ε’γ=hv’ — энергия рассеянного фотона. Подставив в выражение (5.2) значения величин и представив (5.3) в соответствии с рис. 3, получим — энергия электрона после столкновения (используется релятивистская формула, так как скорость электрона отдачи в общем случае значительна ε’γ=hv’ — энергия рассеянного фотона. Подставив в выражение (5.2) значения величин и представив (5.3) в соответствии с рис. 3, получим
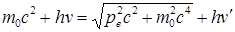 (5.4) (5.4)
(рис. 3)
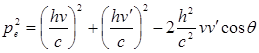 (5.5) (5.5)
Решая уравнения (206.4) и (206.5) совместно, получим
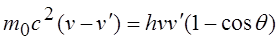
Поскольку ν=c/λ, ν’=c/λ’ и ∆λ=λ’-λ, получим (5.6)
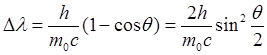 (5.6) (5.6)
Выражение (5.6) есть не что иное, как полученная экспериментально Комптоном формула (5.1). Подстановка в нее значений h, mQи с дает комптоновскую длину волны электрона λс=h/(m0c)=2,426 пм.
Наличие в составе рассеянного излучения несмещенной линии (излучения первоначальной длины волны) можно объяснить следующим образом. При рассмотрении механизма рассеяния предполагалось, что фотон соударяется лишь со свободным электроном. Однако если электрон сильно связан с атомом, как это имеет место для внутренних электронов (особенно в тяжелых атомах), то фотон обменивается энергией и импульсом с атомом в целом. Так как масса атома по сравнению с массой электрона очень велика, то атому передается лишь ничтожная часть энергии фотона. Поэтому в данном случае длина волны λ рассеянного излучения практически не будет отличаться от длины волны λ падающего излучения.
Из приведенных рассуждений следует также, что эффект Комптона не может наблюдаться в видимой области спектра, поскольку энергия фотона видимого света сравнима с энергией связи электрона с атомом, при этом даже внешний электрон нельзя считать свободным.
Эффект Комптона наблюдается не только на электронах, но и на других заряженных частицах, например протонах, однако из-за большой массы протона его отдача «просматривается» лишь при рассеянии фотонов очень высоких энергий.
Как эффект Комптона, так и фотоэффект на основе квантовых представлений обусловлены взаимодействием фотонов с электронами. В первом случае фотон рассеивается, во втором — поглощается. Рассеяние происходит при взаимодействии фотона со свободным электроном, а фотоэффект — со связанными электронами. Можно показать, что при столкновении фотона со свободным электроном не может произойти поглощения фотона, так как это находится в противоречии с законами сохранения импульса и энергии. Поэтому при взаимодействии фотонов со свободными электронами может наблюдаться только их рассеяние, т. е. эффект Комптона.
|
|
|
 Скачать 4.58 Mb.
Скачать 4.58 Mb.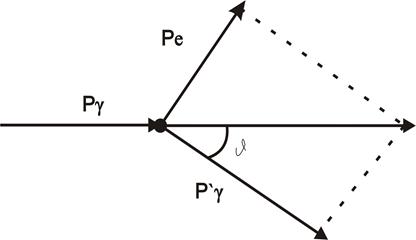

 Устройство фоторезистора показано на рис. 5.11. Светочувствительный элемент фоторезистора представляет собой прямоугольную или круглую таблетку, спрессованную из полупроводникового материала, или тонкую пленку 1 на стеклянной, слюдяной или керамической подложке 2. На концах светочувствительного элемента создают электроды 3 с малым сопротивлением.
Устройство фоторезистора показано на рис. 5.11. Светочувствительный элемент фоторезистора представляет собой прямоугольную или круглую таблетку, спрессованную из полупроводникового материала, или тонкую пленку 1 на стеклянной, слюдяной или керамической подложке 2. На концах светочувствительного элемента создают электроды 3 с малым сопротивлением.
