Физике. физика. Электродинамика Электрические токи в металлах, вакууме и газах. Электрический ток в жидкостях
 Скачать 4.58 Mb. Скачать 4.58 Mb.
|
1. Работа выхода электронов из металла.Электроны проводимости в кристалле находятся в потенциальной яме. Выход из нее требует совершения работы по преодолению силы, действующей на электрон со стороны кристалла. Найдем эту силу. Обладая энергией теплового движения, электроны могут выскакивать из кристалла на расстояние в несколько периодов. Вышедший из кристалла и находящийся у его поверхности на расстоянии х электрон индуцирует в металле заряд е+ (рис.97). Этот наведенный заряд действует на вышедший электрон так, как если бы он был сосредоточен под поверхностью металла на глубине х в точке, симметричной той, в которой находится электрон (см. Эл-во §5). Индуцированный заряд е+ называется электрическим изображением заряда е-. Оба точечные заряда притягиваются друг к другу с силой Кулона 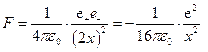 . (14.1) . (14.1)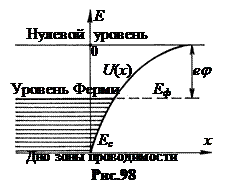 Но это и есть сила притяжения металлом вышедшего из него электрона. Под действием этой силы электрон втягивается обратно в металл. Чтобы удалить электрон из металла, надо совершить работу по преодолению этой силы, перемещая электроны на бесконечность из точки, расположенной на расстоянии х0 от поверхности металла. В качестве х0 можно взять межатомное расстояние. На рис.98 показана зависимость потенциальной энергии электрона от расстояния х до атомной плоскости – стенки металла. Энергетическое расстояние еj от уровня Ферми до нулевого уровня называют термодинамической работой выхода электрона, величину j – потенциалом выхода. Уровень Ес обозначает дно зоны проводимости, где Е = 0. У металлов работа выхода еj заключена в пределах 1,8 ¸ 5,3 эВ. Меньше всего она у щелочных металлов, больше – у золота, серебра, платины (табл. 14.1).
 Большое влияние на работу выхода оказывают мономолекулярные адсорбированные слои. Например, слой атомов цезия Cs на вольфраме W (рис.99). Цезий щелочной металл. Его внешний, валентный электрон связан с ядром значительно слабее, чем валентные электроны в вольфраме. Поэтому атомы цезия отдают вольфраму свои валентные электроны и превращаются в положительные ионы. Между этими ионами и их электрическими изображениями в вольфраме возникает сила притяжения, удерживающая ионы цезия на поверхности вольфрама. Поле этого двойного электрического слоя помогает выходу электронов из вольфрама. По этому в присутствии слоя цезия работа выхода электрона из вольфрама уменьшается с 4,54 эВ до 1,38 эВ. Подобно цезию действуют одноатомные слои бария Ba, церия Cе, тория Th и др. 5. Эмиссионные явления. С повышением температуры металла поверхность Ферми разрыхляется, энергия электронов увеличивается, и они поднимаются на более высокие уровни (рис.100). Соответственно уменьшается работа выхода электронов. Поэтому концентрация вылетевших из кристалла электронов в пристеночном слое растет. Процесс испускания электронов нагретым металлом называется термоэлектронной эмиссией. Формально термоэлектронная эмиссия есть всегда, когда Т > 0 К. Но заметной она становится при температурах Т > 800 К. 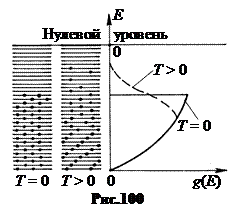 Облако термоэлектронов находится в динамическом равновесии. Число вылетевших из металла электронов в каждый промежуток времени примерно равно числу электронов, втянутых в металл. Поэтому суммарный ток эмиссии равен нулю. 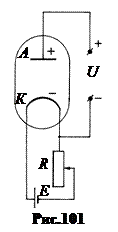 На основе термоэлектронной эмиссии построен ламповый вакуумный диод (рис.101). Здесь К – катод, обычно нагреваемая вольфрамовая спираль, А – анод, холодная металлическая пластина обычно цилиндрической формы. По оси этого цилиндра натягивается спираль катода. Оба электрода помещаются в стеклянный сосуд с высоким вакуумом. 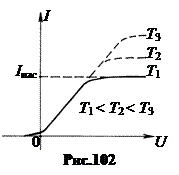 Если между катодом и анодом создавать электрическое поле с напряжением U, как показано на рис.101, то термоэлектроны под действием этого поля будут перемещаться от катода к аноду. Возникает электрический ток в вакууме. Вольтамперная характеристика вакуумного диода показана на рис.102. С повышением анодного напряжения U ток I через анод растет почти пропорционально U. Но при достижении некоторого значенья Iнас перестает увеличиваться. Это предельное значение Iнас называют ток насыщением. Он возникает тогда, когда все электроны, вылетевшие из нагретого катода, захватываются полем и переносятся к аноду. С повышением температуры катода ток насыщения увеличивается. Разделив ток насыщения на поверхность S катода, получаем плотность тока насыщения jнас = iнасçS. В 1901г. Оуэн Ричардсон, исходя из классических представлений, теоретически нашел зависимость плотности тока насыщения от температуры поверхности катода. Уточненная Дешманом в 1923г. с учетом квантовых представлений, зависимость jнас(Т) имеет вид: Здесь еj – работа выхода, А – константа, имеющая разное значение у разных металлов и колеблющаяся около теоретического значения А= 1,2·106 Аç(м2К2). 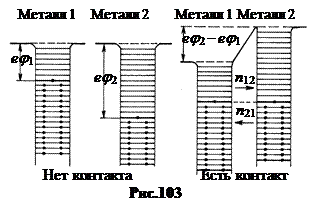 6. Ионизация газов. Газовый разряд. Плазма и ее свойства. Электрическим разрядом в газах называется процесс перемещения электрических зарядов в пространстве, заполненном газом или парами металлов, протекающий под действием электрического поля. Существуют следующие главные формы газового разряда: темный, тлеющий и дуговой. Кроме того, существуют также переходные формы разряда - искровой, коронный, а также особые формы разряда - безэлектродный и импульсный. Для характеристики состояния вещества в условиях электрического разряда было введено понятие о газоразрядной плазме, а затем обобщенно на другие явления природы. Под плазмой понимают газ, состоящий из положительно и отрицательно заряженных частиц в таких пропорциях, что общий заряд равен нулю и обладающий хорошей электропроводностью и собственным свечением. Говоря о плазме как о четвертом состоянии вещества, следует подчеркнуть величайший интерес к изучению ее свойств в настоящее время, определяемый следующими причинами: 1.Плазма является основным состоянием вещества в известной нам части вселенной, а не изредка встречающимся состоянием газа (99% массы всей солнечной системы). 2.Второй причиной является все растущее значение приборов, использующих плазму в уже сложившихся областях техники(радиоэлектроника, спектральный анализ, электросварка, плазмохимия и др.). 3.Третья причина — это совершенно необычные свойства плазмы, которые сулят возможность новых, неожиданных ее применений. В известной нам части плазма тлеющего разряда используется в лампах дневного света, в газоразрядных трубках, заполненных гелием, неоном или другими газами, для декоративных и рекламных целей. Искровой разряд используется для предохранения электрических линий передач от перенапряжения (искровой разрядник), а также для воспламенения горючей смеси в двигателе внутреннего сгорания. На искровом разряде основана электроискровая обработка металлов (резание, сверление, доводка и т.д.). Дуговой разряд используется для сварки металлов, выплавки специальных сталей (дуговая печь), освещения (дуговой фонарь, прожектор), в качестве источника ультрафиолетовых лучей (ртутные дуговые Лампы). В устройствах для получения стабильных струй плазмы (плазматронах) дуговой разряд используется с успехом как источник тепла для химико-металлургической и технологической обработки самых разнообразных материалов, что значительно повышает эффективность этих процессов. С помощью плазматронов, например, в строительстве освоена технология изготовления фундаментов на месте объекта из любого грунта, а в промышленности получают ряд тугоплавких порошков, которые практически нельзя получить другими способами. Порошковая технология в металлургии получает широкое применение из-за возможности повышения прочности, особенно в области высоких температур, и коррозиусточивости. Например, напыление порошка на поверхность стальных деталей практически в 10 раз увеличивает их стойкость к коррозии. Огромный экономический эффект дает метод восстановления изношенных деталей. Нанося порошок на поверхность, восстанавливают детали. И здесь экономия огромна: не надо делать новые детали, тратя на это материалы, энергию, груд. Широко используются и электронно-лучевые установки. На них можно производить следующие технологические процессы: локальный переплав, плавку, сварку (особенно в космосе, где условия подходящие), испарение материалов, размерную обработку, термообработку и другие. В настоящее время все большее значение приобретают металлические монокристаллы высокой частоты из-за весьма полезных свойств в технике. Например, обычное железо хрупко при температуре - 40°С, а чистое железо пластично при температуре -196°С. Для получения металлического монокристалла применяются ряд методов. Один из самых распространенных - зонная плавка электронным лучом. Этот метод обеспечивает высокую степень чистоты металла и обработку деталей любой твердости. Принципиально новые технологии позволяют создать выведенный в атмосферу концентрированный пучок электронов. Выпускаемые промышленностью полностью автоматизированные установки обеспечивают электронные пучки с энергией 1,5 - 2,0 МэВ и мощностью сотни киловатт. Область их применения весьма широка от очистки воды, зерна, медицинских инструментов до металлургических процессов. 7. Магнитные моменты электронов и атомов. МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВА Рассматривая действие магнитного поля на проводники с током и на движущиеся заряды, мы не интересовались процессами, происходящими в веществе. Свойства среды учитывались формально с помощью магнитной проницаемости. Для того чтобы разобраться в магнитных свойствах сред и их влиянии на магнитную индукцию, необходимо рассмотреть действие магнитного поля на атомы и молекулы вещества. Опыт показывает, что все вещества, помещенные в магнитное поле, намагничиваются. Рассмотрим причину этого явления с точки зрения строения атомов и молекул, положив в основу гипотезу Ампера, согласно которой в любом геле существуют микроскопические токи, обусловленные движением электронов в атомах и молекулах Для качественного объяснения магнитных явлений с достаточным приближением можно считать, что электрон в атоме движется по круговым орбитам. Электрон, движущийся по одной из таких орбит, эквивалентен круговому току, поэтому он обладает орбитальным магнитным моментом модуль которого Pm = I S = evS, (4.1) где I = e ν - сила тока, ν - частота вращения электрона по орбите, S - площадь орбиты. Если электрон движется против часовой стрелки (Рис. 56), то ток направлен против часовой стрелки, и вектор в соответствии с правилом вита направлен перпендикулярно плоскости орбиты электрона. С другой стороны, движущийся по орбите электрон обладает механическим моментом импульса , модуль которого Lc=mvr = 2mvS, (4.2)
где величина называется г и р о магнитным отношением орбитальных моментов (общепринято писать со знаком минус, указывающим на то, что направления моментов противоположны). Это отношение, определяемое универсальными постоянными, одинаково для любой орбиты, хотя для разных орбит значения V и г различны. Формула выведена для круговой орбиты, но она справедлива и для эллиптических орбит. Экспериментальное определение гиромагнитного отношения проведено в опытах Энштейна и де Гааза, которые наблюдали поворот свободно подвешенного на тончайшей кварцевой нити железного стержня при его намагничивании во внешнем магнитном поле. При исследовании вынужденных крутильных колебаний стержня определялось гиромагнитное отношение, которое оказалось равным . Таким образом, знак носителей, обусловливающий молекулярные токи, совпадал со знаком заряда электрона, а гиромагнитное отношение оказалось в два раза большим, чем введенная ранее величина g. Для объяснения этого результата, имевшего большое значение для дальнейшего развития физики, было предположено, а впоследствии доказано, что, кроме орбитальных моментов, электрон обладает собственным механическим моментом и м п у л ь с a называемым спином. Считалось, что спин обусловлен вращением электрона вокруг своей оси, что привело к целому ряду противоречий. В настоящее время установлено, что спин является неотъемлемым свойством электрона, подобно его заряду и массе. Спину электрона соответствует собственный (спиновый) магнитный момент , пропорциональный и направленный в противоположную сторону: . (4.3) Величина gs называется гиромагнитным отношением спиновых моменто в. Проекция собственного магнитного момента на направление вектора может принимать только одно из следующих двух значений: где (h - постоянная Планка), μb -магнетон Вора, являющийся единицей магнитного момента электрона. В общем случае магнитный момент электрона складывается из орбитального и спинового магнитных моментов. Магнитный момент атома, следовательно, складывается из магнитных моментов входящих в его состав электронов и магнитного момента ядра (обусловлен магнитными моментами входящих в ядро протонов и нейтронов). Однако магнитные момент ядер в тысячи раз меньше магнитных моментов электронов, поэтому ими пренебрегают Таким образом, общий магнитный момент атома (молекулы) равен векторной сумме магнитных моментов (орбитальных и спиновых) входящих в атом (молекулу) электронов: Еще раз обратим внимание на то, что при рассмотрении магнитных моментов электронов и атомов мы пользовались классической теорией, не учитывая ограничений, накладываемых на движение электронов законами квантовой механики. Однако это не противоречит полученным результатам, т.к. для дальнейшего объяснения намагничивания веществ существенно лишь то, что атомы обладают магнитными моментами. 8.Условия на границе раздела двух магнетиков. Классификация магнетиков Рассмотрим условия для векторов и на границе раздела двух однородных магнетиков (магнитные проницаемости и при отсутствии на границе тока проводимости. Построим вблизи границы раздела магнетиков 1 и 2 прямой цилиндр ничтожно малой высоты, одно основание которого находится в первом магнетике, другое — во втором (рис. 190). Основания настолько малы, что в пределах каждого из них вектор одинаков. Согласно теореме Гаусса (120.3), (нормали и к основаниям цилиндра направлены противоположно). Поэтому (134.1)  Рис. 190 Заменив, согласно , проекции вектора проекциями вектора , умноженными на , получим 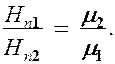 (134.2) (134.2)Вблизи границы раздела двух магнетиков 1 и 2 построим небольшой замкнутый прямоугольный контур ABCDA длиной l, ориентировав его так, как показано на рис. 191. 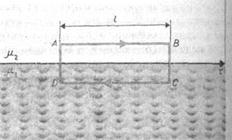 Рис.191 Согласно теореме (133.10) о циркуляции вектора , 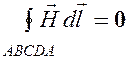 (токов проводимости на границе раздела нет), откуда (знаки интегралов по АВ и CD разные, так как пути интегрирования противоположны, а интегралы по участкам ВС и DA ничтожно малы). Поэтому 9. Диа-и парамагнетизм. Всякое вещество является магнетиком, т.е. оно способно под действием магнитного поля приобретать магнитный момент (намагничиваться). Для понимания механизма этого явления необходимо рассмотреть действие магнитного поля на движущиеся в атоме электроны.
составляющая магнитного поля, направленная противоположно внешнему полю. Наведенные составляющие магнитных полей атомов (молекул) складываются и образуют собственное магнитное поле вещества, ослабляющее внешнее магнитное поле. Этот эффект получил название диамагнитного эффекта, а вещества, намагничивающиеся во внешнем магнитном поле против направления поля, называются диамагне-тиками. В отсутствие внешнего магнитного поля диамагнетик ненамагничен, поскольку в данном случае магнитные моменты электронов взаимно компенсируются, и суммарный магнитный момент атома (он равен векторной сумме орбитальных и спиновых магнитных моментов, составляющих атом электронов) равен нулю. К диамагнетикам относятся многие металлы (например, Bi, Ag, Au, Си), большинство органических соединений, смолы, углерод и т.д. Так как диамагнитный эффект обусловлен действием внешнего магнитного поля на электроны атомов вещества, то диамагнетизм свойственен всем веществам. Однако наряду с диамагнитными веществами существуют и парамагнитные вещества, намагничивающиеся во внешнем магнитном поле по направлению поля. У парамагнитных веществ при отсутствии внешнего магнитного поля магнитные моменты электронов не компенсируют друг друга, и атомы (молекулы) парамагнетиков всегда обладают магнитным моментом. Однако вследствие теплового движения молекул их магнитные моменты ориентированы беспорядочно, поэтому парамагнитные вещества магнитными свойствами не обладают. При внесении парамагнетика во внешнее магнитное поле устанавливается преимущественная ориентация магнитных моментов атомов по полю (полной ориентации препятствует тепловое движение атомов). Таким образом, парамагнетик намагничивается, создавая собственное магнитное поле, совпадающее по направлению с внешним полем и усиливающее его. Этот эффект называется парамагнитным. При ослаблении внешнего магнитного поля до нуля ориентация магнитных моментов вследствие теплового движения нарушается, и парамагнетик размагничивается. К парамагнетикам относятся редкоземельные элементы, Pt, A1 и т.д. Диамагнитный эффект наблюдается и в парамагнетиках, но он значительно слабее парамагнитного и поэтому остается незаметным. Подводя итог качественному рассмотрению диа- и парамагнетизма, еще раз отметим, что атомы всех веществ являются носителями диамагнитных свойств. Если магнитный момент атомов велик, то парамагнитные свойства преобладают над диамагнитными и вещество является парамагнетиком; если магнитный момент атомов мал, то преобладают диамагнитные свойства и вещество является диамагнетиком. 10.Влияние среды на магнитное взаимодействие. Электронный парамагнитный резонанс
Электронный парамагнитный резонанс (ЭПР) был открыт Евгением Константиновичем Завойским в Казанском Университете в 1944 году. Он заметил, что монокристалл , помещенный в постоянное магнитное поле (4 мТл) поглощает микроволновое излучение определенной частоты (около 133 МГц). Суть данного эффекта заключается в следующем. Электроны в веществах ведут себя как микроскопические магниты. Если поместить вещество в постоянное внешнее магнитное поле и воздействовать на него радиочастотным полем, то в разных веществах они будут переориентироваться по-разному и поглощение энергии будет избирательным. Возврат электронов к исходной ориентации сопровождается радиочастотным сигналом, который несет информацию о свойствах электронов и их окружении. Расщепление Зеемана соответствует радиочастотному диапазону. Ширина линий спектра расщеплённого состояния определяется взаимодействием спинов электронов с их орбитальными моментами. Это определяет время релаксационных колебаний атомов как результат их взаимодействия с окружающими атомами. Поэтому ЭПР может служить средством исследования структуры внутреннего строения кристаллов и молекул, механизма кинетики химических реакций и других задач. 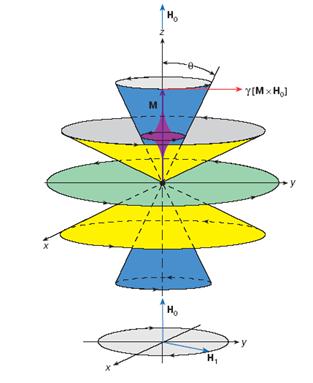 Рис. 5.5 Прецессия магнитного момента (М) парамагнетика в постоянном магнитном поле . Рис. 5.5 иллюстрирует явление прецессии электрона в магнитном поле. Под действием вращательного момента, создаваемого полем , магнитный момент совершает круговые вращения по образующей конуса с ларморовской частотой . При наложении переменного магнитного поля, вектор напряженности совершает круговое движение с ларморовской частотой в плоскости, перпендикулярной вектору . При этом происходит изменение угла прецессии, приводящее к опрокидыванию магнитного момента (М). Увеличение угла прецессии сопровождается поглощением энергии электромагнитного поля, уменьшение угла - излучением с частотой . Практически удобнее использовать момент наступления резкого поглощения энергии внешнего поля при постоянной частоте и изменяемой индукции магнитного поля. Чем сильнее взаимодействие между атомами, молекулами тем шире спектр ЭПР. Это позволяет судить о подвижности молекул, вязкости среды ( > ). 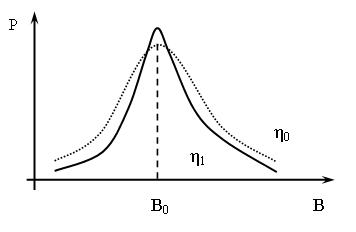 Рис. 5.6 Зависимость поглощающей способности энергии внешнего поля веществом от величины его вязкости. , (5.5) - гиромагнитное отношение. Например, при частота электромагнитного воздействия должна находиться в пределах . Данный метод, представляющий собой один из видов спектроскопии, применяется при исследовании кристаллической структуры элементов, химии живых клеток, химических связей в веществах и т.д. На рис. 5.6 представлена структурная схема ЭПР-спектрометра. Принцип его работы основан на измерении степени резонансного поглощения веществом проходящего через него электромагнитного излучения при изменяющейся напряженности внешнего магнитного поля. 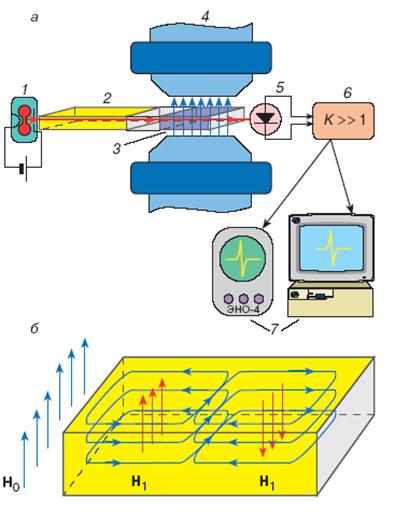 Рис. 5.7 Схема спектрометра ЭПР (а) и распределение силовых линий магнитного и электрического полей в резонаторе. 1 – генератор микроволнового излучения, 2 – волновод, 3- резонатор, 4 – магнит, 5 – детектор микроволнового излучения, 6 – усилитель сигнала ЭПР, 7 – регистрирующие устройства (ЭВМ или осциллограф). Открытие ЭПР послужило основой для разработки ряда других методов изучения строения веществ, таких как акустический парамагнитный резонанс, ферро- и антиферромагнитный резонанс, ядерный магнитный резонанс. При явлении акустического парамагнитного резонанса переходы между подуровнями инициируются наложением высокочастотных звуковых колебаний; в результате возникает резонансное поглощение звука. Применение метода ЭПР дало ценные данные о строении стекол, кристаллов, растворов; в химии этот метод позволил установить строение большого числа соединений, изучить цепные реакции и выяснить роль свободных радикалов (молекул, обладающих свободной валентностью) в появлении и протекании химических реакций. Тщательное изучение радикалов привело к решению ряда вопросов молекулярной и клеточной биологии. Метод ЭПР – очень мощный исследовательский инструмент, он практически незаменим при изучении изменений в структурах, в том числе и в биологических. Чувствительность метода ЭПР очень высока и составляет парамагнитных молекул. На применении ЭПР основан поиск новых веществ для квантовых генераторов; явление ЭПР используется для генерации сверхмощных субмиллиметровых волн. 11. Вихревое электрическое поле. Ток смещения Закон электромагнитной индукции Фарадея, определяющий ЭДС индукции, возбуждаемую в неподвижном замкнутом проводящем контуре 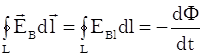 , где , где По определению магнитный поток 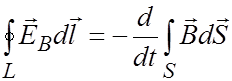 . Считая поверхность интегрирования S, образованную неподвижным контуром L, неподвижной, операции дифференцирования и интегрирования можно поменять местами: . Считая поверхность интегрирования S, образованную неподвижным контуром L, неподвижной, операции дифференцирования и интегрирования можно поменять местами: 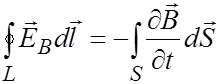 (символ частной производной подчеркивает тот факт, что интеграл (символ частной производной подчеркивает тот факт, что интеграл 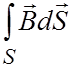 является функцией только от времени) – уравнение Максвелла. является функцией только от времени) – уравнение Максвелла.Циркуляция вектора напряженности электростатического поля ( |

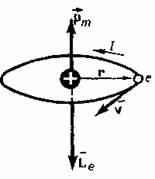 Рис. 56
Рис. 56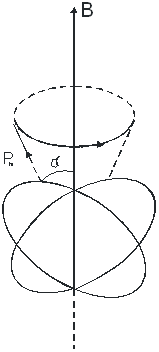 Рис. 57
Рис. 57