Физике. физика. Электродинамика Электрические токи в металлах, вакууме и газах. Электрический ток в жидкостях
 Скачать 4.58 Mb. Скачать 4.58 Mb.
|
Абразивная суспензия Зерна абразива по твердости не должны уступать обрабатываемому материалу. Обычно применяют карбид бора, который хорошо смачивается водой и благодаря сравнительно небольшой плотности удовлетворительно переносится жидкостью. Карбид кремния, электрокорунд — применяются для изготовления деталей из стекла, германия. Если производительность обработки стекла карбидом бора принять за единицу, то производительность обработки карбидом кремния — 0,8…0,85, а электрокорундом — 0,7…0,75. В качестве жидкости обычно используют воду, обладающую малой вязкостью, удовлетворительной смачивающей способностью и хорошими охлаждающими свойствами. В воду добавляют ингибитор коррозии. Использование добавок, оказывающих химическое действие на обрабатываемый материал — 15%-ного водного раствора сернокислой меди — повышает производительность обработки твердых сплавов в 1,7…2,5 раза. Размер зерна абразива — ширина зерна под микроскопом. Уменьшение размера абразивных зерен вызывает снижение производительности (особенно если размеры зерна меньше амплитуды колебаний). С другой стороны, чем меньше зерно, тем выше точность изготовления. Концентрация абразива в суспензии Оптимальная концентрация — по всей обрабатываемой поверхности укладывается один слой зерен абразива. При большей концентрации (в несколько слоев) — увеличивается доля работы, идущей на измельчение самих зерен. Амплитуда и частота колебаний инструмента определяют скорость продольных колебаний инструмента, то есть главного движения резания где f — частота колебаний (16…30кГц); A — амплитуда колебаний инструмента, мкм. Чем больше амплитуда и частота колебаний, тем выше производительность ( ). Оптимальная амплитуда колебаний инструмента связана со средним размером абразивного зерна основной фракции. При >1 происходит главным образом не внедрение зерен в обрабатываемую поверхность, а их дробление. Если амплитуда колебаний мала, а зерна абразива крупнее <0,5, импульс ударной силы, воздействующий на зерно, недостаточен для внедрения зерен в обрабатываемый материал и его разрушения. Максимальная производительность достигается при условии =0,6…0,8. Предельно допустимая амплитуда колебаний ограничивается, кроме вышеизложенных соображений, усталостной прочностью материала инструмента и концентратора. Статическая нагрузка. При УЗО инструмент прижимается к поверхности заготовки с постоянной силой . Эта сила (сила подачи) оказывает значительное влияние не только на значение ударных импульсов, но и на состояние зерен и концентрацию абразива под торцом инструмента. Оптимальное значение зависит от площади и конфигурации инструмента, амплитуды, среднего размера зерен и свойств обрабатываемого материала. Увеличение (в определенных пределах) приводит к увеличению импульса ударных сил и глубины внедрения зерен абразива, то есть к увеличению производительности. С другой стороны, увеличение уменьшает расстояние между инструментом и обрабатываемой поверхностью заготовки и ухудшает условия поступления в рабочую зону свежего абразива и удаление из нее продуктов износа 2.2 Точность размерной обработки Точность УЗ размерной обработки, т.е. стабильность зазора между контурами изделия и инструмента, определяется многими факторами: геометрическая точность станка и его приспособлений, размер зерен абразива, твердость обрабатываемого материала, форма инструмента и размер поперечных колебаний. Минимальная погрешность ограничивается предельными изменениями размера бокового зазора. Обычно этот размер в 1,5 раза больше среднего размера зерна абразива основной фракции. В основном изнашивается торец инструмента. Продольный относительный износ (отношение длины изношенной части к глубине обработанной полости, в %) инструмента зависит главным образом от физико-механических свойств заготовки и материала инструмента, толщины стенок инструмента и зернистости абразива. Поперечный износ происходит вследствие действия абразива, находящегося между боковой поверхностью инструмента и стенками обрабатываемого отверстия — на инструменте появляется конусность. Особенно увеличивается поперечный износ при использовании кольцевого инструмента с толщиной стенки менее 1 мм. Оптимальная толщина стенки должна быть в пределах 1…1,5 мм. Интенсивность износа увеличивается при плохих условиях подвода свежей абразивной суспензии и отвода продуктов обработки. В то же время сила подачи и амплитуда не оказывают существенного влияния на его износ. Чтобы уменьшить износ инструмента прежде всего необходимо подбирать материал, обладающий достаточной износостойкостью. Например, при обработке стекла инструмент должен быть из твердого сплава, а при обработке твердого сплава – из закаленной инструментальной стали. Целесообразно выполнять инструменты с обратной конусностью или применять “грибковый’’ инструмент с калибрующей ленточкой высотой 1…3 мм. Причем диаметр калибрующей ленточки должен быть на 0,6…1 мм больше диаметра стержня инструмента. За счет этого уменьшается сила трения…, улучшается циркуляция суспензии, хорошо удаляются продукты обработки. Из — за поперечных колебаний инструмента происходит “разбивание” отверстия. Может исказиться и форма отверстия. Обычно при строгой прямолинейности осей и соосности преобразователя, концентратора и инструмента, а также при точной выверке инструмента и заготовки некруглость отверстий, получаемых при чистовых операциях, не превышает 10 мкм (в неблагоприятных случаях – 30…60 мкм) Разбивание отверстий возрастает с увеличением размеров абразивных зерен и глубины обработки. Для уменьшения конусности сквозных отверстий их обрабатывают последовательно с двух сторон. При сквозном прошивании, сверлении и разрезании используется инструмент, состоящий, из двух участков: чернового и чистового (диаметр чистового больше диаметра чернового участка). При УЗ размерной обработке погрешность изготовления достигает 20 мкм. 2.3 Качество поверхности Шероховатость поверхности при УЗО зависит от размеров зерен абразива, физико-механических свойств заготовки, амплитуды колебаний инструмента, шероховатости поверхности инструмента и типа жидкости, несущей абразив. Наибольшее влияние на шероховатость оказывает зернистость абразива. Шероховатость пропорциональна зернистости. Свойства обрабатываемого материала — структура (крупнозернистая) определяют шероховатость. Чем выше амплитуда колебаний инструмента, тем более шероховатая поверхность получается при обработке. Если в качестве жидкости, несущей абразив, применить вместо воды машинное масло, то шероховатость поверхности уменьшается, но производительность в несколько раз снижается, ухудшаются условия подвода и циркуляции абразива. Шероховатость обрабатываемой поверхности зависит и от шероховатости рабочих поверхностей инструмента — неровности инструмента копируются на поверхности заготовки. При чистовых операциях высота микронеровностей рабочих поверхностей инструмента должна быть в 2…3 раза меньше требуемой высоты микронеровностей детали. Кроме шероховатости качество обработанной поверхности характеризуется ее структурным состоянием. При УЗО твердых сплавов и закаленных сталей происходит упрочнение поверхностного слоя и появляются сжимающие остаточные напряжения. При УЗО мелкими шлифпорошками (№3) и микропорошками при амплитудах колебаний 15…20мкм шероховатость поверхности =1,2…0,4 мкм, а при доводке =0,2 мкм. 2.4 Производительность размерной УЗО Производительность УЗ размерной обработки зависит в первую очередь от амплитуды колебаний инструмента, физико-механических свойств обрабатываемого материала, состава и свойств абразивной суспензии и способа ее подвода, силы подачи, площади поперечного сечения инструмента, глубины обработки. Она характеризуется скоростью съема материала заготовки и при постоянном поперечном сечении инструмента однозначно определяется скоростью подачи. Производительность можно рассчитать по эмпирической формуле Qs=ψ (А2∙Рст)а∙fв, мм3/мин (4.2) Где – коэффициент, зависящий от свойств обрабатываемого материала и абразивной суспензии; А – амплитуда колебаний инструмента, мкм; – сила подачи, H; f – частота колебаний, Гц; а и в – показатели степени, зависящие от условий обработки (а=0,5…1; в=0,5…1). Чем выше твердость абразива и размер зерен, тем больше съем материала и производительность (учитывает коэффициент ). Оптимальная сила подачи подбирается обычно экспериментально и составляет при размерной обработке =30…200 H. Давление прижима инструмента Производительность обработки зависит от глубины и площади обрабатываемого отверстия, что отражается в значениях показателей степени а и в. Продольный и поперечный износ инструмента влияет на производительность (так как амплитуда колебаний уменьшается). Амплитуда колебаний уменьшается и при увеличении площади инструмента. Если площадь больше, то хуже условия циркуляции абразива. Повысить производительность можно различными способами. Улучшение условий циркуляции абразивной суспензии: — периодически поднимать и опускать инструмент; — подвод суспензии через полый концентратор; — подвод суспензии фонтаном снизу; — применение инструмента с кольцевыми и спиральными канавками на боковых поверхностях; — применение инструмента с обратной конусностью; — прокачка суспензии под давлением (0,1…0,5 МПа); — отсасывание суспензии; — вращение заготовки или инструмента во время обработки; — создавая эксцентриситет осей вращения инструмента и заготовки. Увеличение скорости главного движения (продольных колебаний инструмента) за счет применения материалов с высоким сопротивлением усталости. Для увеличения сопротивления усталости проводят: дробеструйный наклеп, гидрополирование, ультразвуковую обработку. В настоящее время широко применяется ультразвуковая обработка алмазным инструментом. 11 Колебательные процессы в электричестве Колебательные системы служат для создания электрических колебаний, их усиления, излучения электромагнитной энергии в пространство и выделения колебаний определенной частоты при приеме. В радиотехнических устройствах в качестве такой системы используется колебательный контур, представляющий собой замкнутую электрическую цепь, состоящую из конденсатора С и катушки индуктивности L. Рассмотрим работу идеального колебательного контура, т. е. контура, в котором отсутствуют потери энергии. При подключении контура (рис. а) к источнику постоянного тока конденсатор С заряжается. Через некоторое время напряжение на его пластинах становится максимальным Uмах, равным напряжению на зажимах источника тока. При этом вся энергия Е=С U2мах : 2,запасенная контуром, оказывается сосредоточенной в электрическом поле конденсатора. При отключении колебательного контура от источника тока конденсатор разряжается. В контуре появляется разрядный ток i, а вокруг витков катушки индуктивности L возникает магнитное поле (рис. б). Процесс разряда конденсатора происходит не мгновенно благодаря возникновению ЭДС самоиндукции катушки. Чем больше индуктивность катушки и емкость конденсатора, тем дольше происходит разряд. Через некоторое время конденсатор полностью разряжается, и напряжение на нем становится равным нулю, а ток в катушке достигает максимального значения. В магнитном поле катушки запасается энергия Ем = L I2мах : 2. 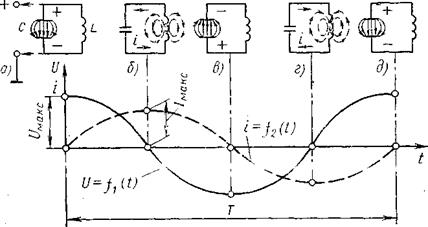 Процесс генерирования электрических колебаний Таким образом, энергия электрического поля конденсатора преобразовывается в энергию магнитного поля катушки индуктивности. В дальнейшем, разрядный ток, достигнув максимального значения, начинает уменьшаться. При этом появляется ЭДС самоиндукции обратного направления, которая препятствует убыванию тока. Под действием этой ЭДС конденсатор заряжается. Через некоторое время ток заряда полностью прекратится, напряжение на конденсаторе становится максимальным, но с обратным знаком (рис. в). После этого конденсатор вновь начинает разряжаться, но ток через катушку пойдет в обратном направлении (рис. г). Колебания, которые возникают в контуре без непрерывного воздействия источника переменной ЭДС, называются свободными или собственными колебаниями. Их период Т0 (с) и частота f0 (Гц) зависят от величины индуктивности L (Гц) катушки и емкости С (Ф) конденсатора: f0 = 1: Т0 Процессы протекающие в идеальном контуре показывают, что свободные электрические колебания являются гармоническими и имеют незатухающий характер. Так как реальный контур обладает активным сопротивлением потерь R, свободные колебания в нем затухают с течением времени. Качество контура характеризуется добротностью Q, которая показывает, во сколько раз волновое (характеристическое) сопротивление контура больше сопротивления потерь R. Чем выше добротность, тем меньше затухают свободные колебания в контуре. Принято считать контуры хорошими, если добротность превышает 100. Добротность плохих контуров менее 20. Для существования незатухающих колебаний в реальном контуре необходимо восполнять расход энергии на потери в контуре от внешнего источника переменной ЭДС. Колебания, которые совершаются в контуре при непрерывном воздействии на него источника переменной ЭДС, называются вынужденными. В том случае, если частота вынужденных колебаний совпадает с частотой свободных колебаний контура, в нем возникает явление электрического резонанса. Оно характеризуется возникновением незатухающих электрических колебаний в контуре при незначительном расходе энергии от источника тока, который необходим лишь для покрытия потерь на активном сопротивлении контура 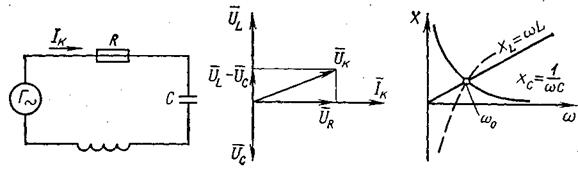 Последовательный колебательный контур: электрическая схема; б — векторная диаграмма напряжений; в — график изменения реактивных сопротивлений в функции частот колебаний В зависимости от схемы подключения источника к колебательному контуру различают последовательное и параллельное подключение. Соответственно этому и контуры именуются последовательными или параллельными. Радиоволны звуковых и инфразвуковых частот, которые по своей природе являются электромагнитными, не следует смешивать со звуковыми волнами, т. е. упругими механическими колебаниями. Спектр электромагнитных волн охватывает частоты примерно от 10-3 до 1023 Гц. Радиоволны занимают частоты 3—3 1012 Гц и разбиты на 12 диапазонов. По способу распространения различают свободно распространяющиеся радиоволны, земные, тропосферные и ионосферные. Практически используемый в авиации спектр частот радиоволн от 3 - 104 до 3 - 1011 Гц в зависимости от особенностей их распространения разбит на ряд диапазонов.
Виды распространения волн: пространственные, земные, тропосферные, ионосферные. Свободно распространяющимися, или прямыми, называются радиоволны, существующие в свободном пространстве (в пустоте) при отсутствии каких-либо тел и предметов на пути распространения, которые могли бы исказить поле волны. Земными, или поверхностными, называют радиоволны, распространяющиеся непосредственно над поверхностью земли и частично огибающие ее вследствие явления дифракции. Тропосферными называют волны диапазонов частот ОВЧ, УВЧ, СВЧ распространяющиеся за счет рассеяния и отражения от локальных и слоистых неоднородностей тропосферы. Тропосферой называют нижнюю часть атмосферы высотой порядка 12 км. Тропосфера по своему состоянию, неоднородна, поэтому волна, встречая на своем пути неоднородности, рассеивается подобно лучам света в каплях дождя. Ионосферными, или пространственными, называют волны, распространяющиеся вокруг земного шара на сколь угодно большие расстояния за счет однократного или многократного отражения от ионосферы. Ионосферой называют верхнюю часть атмосферы в интервале высот 60—20 000 км. Ионосфера представляет собой несколько расположенных друг над другом слоев ионизированных газов. 12. Амплитуда и фаза вынужденных колебаний. Рассмотрим колебания, которые поддерживаются в системе внешней гармонической силой F = F0Coswt. Такие колебания называются вынужденными. Обратимся вновь к пружинному маятнику. Вспомним уравнения движения этого осциллятора: — уравнение собственных незатухающих колебаний. В системе действует одна упругая сила Fупр = –kx; — собственные затухающие колебания. В системе появилась сила вязкого сопротивления, пропорциональная скорости . В случае вынужденных колебаний кроме двух названных сил — упругой и силы сопротивления, на систему действует ещё одна сила: F = F0Coswt. Введя знакомые обозначения и , представим уравнение движения осциллятора окончательно в таком виде: Опыт показывает, что под действием гармонического возмущающего усилия F = F0Coswt осциллятор совершает гармонические колебания с частотой вынуждающей силы w: х = ACos(wt + a). (13.15) Если частота w известна, то задача сводится к определению амплитуды вынужденных колебаний А и начальной фазы a. Продифференцировав функцию (13.15), подставим ее в уравнение (13.14): Теперь воспользуемся известными тригонометрическими формулами для косинуса и синуса суммы двух углов: Это уравнение представляет собой сумму двух гармонических слагаемых аCos wt + b Sin wt = 0. Последнее равенство возможно в единственном случае, если постоянные во времени a и b равны нулю: а = 0, b = 0. Это означает, что справедливы следующие уравнения: Эти два уравнения содержат только две неизвестные величины: амплитуду А и фазу a вынужденного колебания. Для отыскания амплитуды А можно домножить уравнение (13.16) на Воспользовавшись этим результатом в уравнении (13.17), найдем Cosa: Возведем уравнения (13.18) и (13.19) в квадрат и сложим: Последнее уравнение решим относительно искомой амплитуды колебаний А: 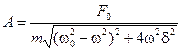 . (13.20) . (13.20)Фазовый сдвиг смещения x относительно возмущающего усилия F найдём непосредственно из уравнения (13.17): Обратимся к анализу полученных результатов. 1) Амплитуда вынужденных колебаний прямо пропорциональна амплитуде возмущающего усилия F0. 2) Если w = 0 — случай приложения статической нагрузки F0, смещение груза будет определяться жёсткостью пружины k: 3) При высоких частотах внешнего усилия (w→¥), амплитуда колебаний А→0. 4) Для отыскания частоты wрез, при которой амплитуда достигает наибольшего значения Арез, нужно найти минимум выражения, стоящего под корнем в знаменателе уравнения (13.20). Продифференцировав это выражение по w, и приравняв результат нулю, получим условие, определяющее wрез: Отсюда следует, что резонансная частота wрез меньше частоты собственных незатухающих колебаний w0: Используя это значение в (13.20), рассчитаем резонансную амплитуду: 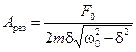 . (13.23) . (13.23)5) Если вязкое сопротивление отсутствует, коэффициент затухания d = = 0 и резонансная амплитуда устремляется в бесконечность. При этом условии резонансная частота, как следует из (13.22), равна частоте собственных незатухающих колебаний осциллятора wрез = w0. 6) С увеличением коэффициента затухания d, резонансная частота и амплитуда колебаний уменьшаются. Все эти закономерности графически представлены на рис. 13.4. 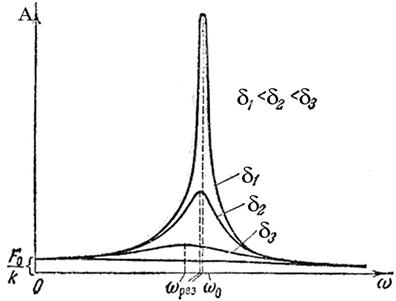 Рис. 13.4 7) При слабом затухании, когда , резонансная амплитуда равна Разделим это выражение на — смещение под действием постоянной силы: Таким образом, добротность осциллятора численно равна отношению резонансной амплитуды к смещению под действием постоянной силы. 8) На рис. 13.5 представлена зависимость фазового сдвига вынужденных колебаний и вынуждающей силы — график функции (13.21). С увеличением частоты вынуждающего усилия a растет, меняясь от 0 до p. В резонансе фазовый сдвиг равен . Эта зависимость a = a(w) меняется с изменением коэффициента затухания. 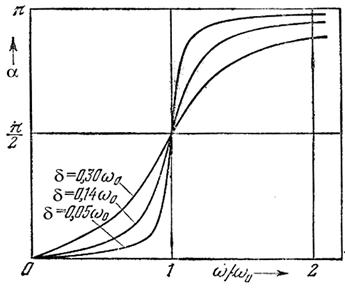 Рис. 13.5 Лекция 14 «Элементы специальной теории относительности» План лекции. 1. Постулаты специальной теории относительности. Преобразования Лоренца. 2. Динамика релятивистского движения. 3. Закон эквивалентности массы и энергии.
В классической механике Ньютона мы изучали законы движения макротел со скоростями, далекими от скорости света (с = 3 × 108 м/с). Такие движения называются нерелятивистскими (классическими), в отличие от релятивистских движений, скорость которых соизмерима со скоростью света. Теоретической основой релятивистской механики является специальная (частная) теория относительности (СТО). Предваряя рассмотрение основных положений этой теории, отметим два важных момента: 1) Релятивистская механика включает в себя и классическую механику как предельный случай движения с малыми скоростями. 2) Все положения СТО имеют сегодня надежное экспериментальное подтверждение. 13.Переменный ток. Резонанс токов и напряжений. Напряжений. Если в цепи переменного тока, содержащей последовательно включенные конденсатор, катушку индуктивности и резистор ωL=1/(ωC), то угол сдвига фаз между током и напряжением обращается в нуль (j=0). Этому условию удовлетворяет частота 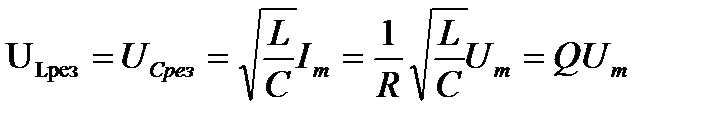 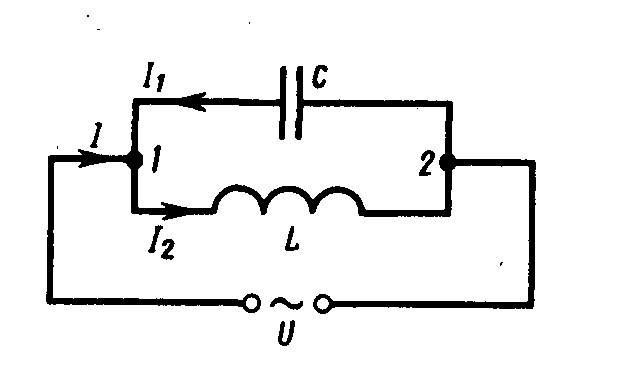 Токов.Рассмотрим цепь переменного тока, содержащую параллельно включенные конденсатор емкостью С и катушку индуктивностью L. Допустим, что активное сопротивление обеих ветвей настолько мало, что им можно пренебречь. Если приложенное напряжение изменяется по закону U= Umсoswt, то, согласно формуле, в одной ветви течет ток Токов.Рассмотрим цепь переменного тока, содержащую параллельно включенные конденсатор емкостью С и катушку индуктивностью L. Допустим, что активное сопротивление обеих ветвей настолько мало, что им можно пренебречь. Если приложенное напряжение изменяется по закону U= Umсoswt, то, согласно формуле, в одной ветви течет ток 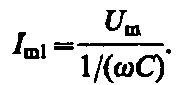 Начальная фаза j1 этого тока по формуле определяется равенством Начальная фаза j1 этого тока по формуле определяется равенством 14.Мощность, выделяемая в цепи переменного тока. Мгновенное значение мощности переменного тока равно произведению мгновенных значений напряжения и силы тока: где Из векторной диаграммы (см. рис. 216) следует, что Такую же мощность развивает постоянный ток I = Im/ . Величины называются соответственно действующими (или эффективными) значениями тока и напряжения. Все амперметры и вольтметры градуируются по действующим значениям тока и напряжения. Учитывая действующие значения тока и напряжения, выражение средней мощности (152.1) можно записать в виде где множитель cos называется коэффициентом мощности. Формула (152.2) показывает, что мощность, выделяемая в цепи переменного тока, в общем случае зависит не только от силы тока и напряжения, но и от сдвига фаз между ними. Если в цепи реактивное сопротивление отсутствует, то cos = 1 и Р = IU. Если цепь содержит только реактивное сопротивление (R = 0), то cos = 0 и средняя мощность равна нулю, какими бы большими ни были ток и напряжение. Если cos имеет значения, существенно меньшие единицы, то для передачи заданной мощности при данном напряжении генератора нужно увеличивать силу тока I, что приведет либо к выделению джоулевой теплоты, либо потребует увеличения сечения проводов, что повышает стоимость линий электропередачи. Поэтому на практике всегда стремятся увеличить cos , наименьшее допустимое значение которого для промышленных установок составляет примерно 0,85. 15.Электромагнитные волны. Уравнение электромагнитной волны. Электромагнитная волна – распространяющееся в среде переменное электромагнитное поле. Теория электромагнитного поля была создана Д. Максвеллом на основе экспериментальных законов электромагнетизма. Согласно этой теории: 1) переменное магнитное поле создает в окружающем его пространстве вихревое электрическое поле; 2) переменное электрическое поле создает в окружающем его пространстве вихревое магнитное поле. Совокупность неразрывно связанных изменяющихся вихревых электрического и магнитного полей называют электромагнитным полем. Из теории Максвелла вытекает: 1)переменное электромагнитное поле распространяется в среде в виде электромагнитной волны; 2)любой движущийся с ускорением (например, колеблющийся ) электрический заряд должен излучать электромагнитную волну. Свойства электромагнитной волны. 1. В электромагнитной волне колеблются векторы и. - напряженность электрического поля, - индукция магнитного поля. 2. Векторы и взаимно перпендикулярны и лежат в плоскости, перпендикулярной направлению распространения волны, т.е. перпендикулярны скорости волны. Значит, электромагнитная волна – поперечная волна (рис.15.2). Векторы , и образуют правую тройку. Если вращать правый винт от вектора к вектору , то поступательное перемещение винта будет совпадать с вектором скорости волны. 3. Векторы иколеблются в одинаковой фазе, одновременно обращаются в нуль и одновременно достигают максимальных значений (рис.15.2). 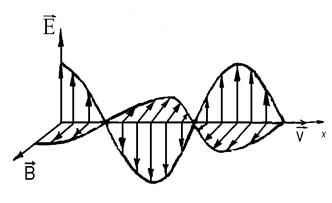 4. Скорость распространения электромагнитных волн в вакууме: 4. Скорость распространения электромагнитных волн в вакууме:= с = 3·108 м/с; в среде: = , (15.5) где и - диэлектрическая и магнитная проницаемости среды. Следовательно, в любой среде скорость распространения электромагнитных волн меньше, чем в вакууме. 5. Связь между длиной, скоростью и Рис.15.2 частотой электромагнитной волны: 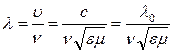 , (15.6) , (15.6)где - длина волны в вакууме; - длина волны в среде. Видим, что длина волны, также как и скорость, уменьшается в среде, частота остается неизменной. Итак, существование электромагнитных волн было предсказано теоретически Максвеллом. Только спустя тридцать лет электромагнитные волны были экспериментально получены Г.Герцем, изучены их свойства. Для получения электромагнитных волн Герц использовал простое устройство, которое в его честь было названо вибратором Герца. Это устройство представляет собой открытый колебательный контур. С этим устройством, с опытами Герца предлагаем познакомиться, прочитав внимательно учебник [2, §49]. Открытие электромагнитных волн имело большое практическое значение для человечества. 16. Энергия, импульс электромагнитного поля. Возможность обнаружения электромагнитных волн указывает на то, что они переносят энергию. Объемная плотность w энергии электромагнитной волны складывается из объемных плотностей wэл (см. (95.8)) и wм (см. (130.3)) электрического и магнитного полей: Учитывая выражение (162.4), получим, что плотности энергии электрического и магнитного полей в каждый момент времени одинаковы, т. е. w33=wtl. Поэтому Умножив плотность энергии w на скорость v распространения волны в среде (см. (162.3)), получим модуль плотности потока энергии: Так как векторы Е и Н взаимно перпендикулярны и образуют с направлением распространения волны правовинтовую систему, то направление вектора [ЕН] совпадает с направлением переноса энергии, а модуль этого вектора равен ЕН. Вектор плотности потока электромагнитной энергии называется вектором Умова — Пойнтинга: Вектор S направлен в сторону распространения электромагнитной волны, а его модуль равен энергии, переносимой электромагнитной волной за единицу времени через единичную площадку, перпендикулярную направлению распространения волны. Если электромагнитные волны поглощаются или отражаются телами (эти явления подтверждены опытами Г. Герца), то из теории Максвелла следует, что электромагнитные волны должны оказывать на тела давление. Давление электромагнитных волн объясняется тем, что под действием электрического поля волны заряженные частицы вещества начинают упорядочение двигаться и подвергаются со стороны магнитного поля волны действию сил Лоренца. Однако значение этого давления ничтожно мало. Можно оценить, что при средней мощности солнечного излучения, приходящего на Землю, давление для абсолютно поглощающей поверхности составляет примерно 5 мкПа. В исключительно тонких экспериментах, ставших классическими, П. Н. Лебедев в 1899 г. доказал существование светового давления на твердые тела, а в 1910 г. — на газы. Опыты Лебедева имели огромное значение для утверждения выводов теории Максвелла о том, что свет представляет собой электромагнитные волны. Существование давления электромагнитных волн приводит к выводу о том, что электромагнитному полю присущ механический импульс. Импульс электромагнитного поля где W— энергия электромагнитного поля. Выражая импульс как р = mс(поле в вакууме распространяется со скоростью с), получим р = mс = W/c, откуда Это соотношение между массой и энергией электромагнитного поля является универсальным законом природы (см. также § 40). Согласно специальной теории относительности, выражение (163.1) имеет общее значение и справедливо для любых тел независимо от их внутреннего строения. Таким образом, рассмотренные свойства электромагнитных волн, определяемые теорией Максвелла, полностью подтверждаются опытами Герца, Лебедева и выводами специальной теории относительности, сыгравшими решающую роль для подтверждения и быстрого признания этой теории. 17.Диполь, его излучение. Согласно представлениям классической электродинамики, электромагнитные волны возбуждаются электрическими зарядами, движущимися с ускорением, в частности, электрической цепью (проводом), ток в которой изменяется. Простейшей излучательной системой является электрический диполь, момент которого (см. параграф 1.5 в конспекте лекций, ч.II) где р0=ql0 – амплитудное значение момента диполя. 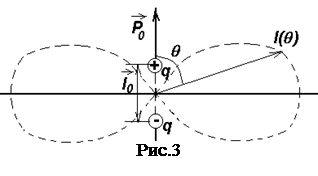 Средняя мощность, излученная диполем за промежуток времени T=2p/w Средняя мощность, излученная диполем за промежуток времени T=2p/w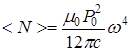 , (22) , (22)т.е. пропорциональна квадрату дипольного момента и четвертой степени круговой частоты. При этом диполь излучает не одинаково в различных направлениях. Интенсивность излучения в волновой зоне (т.е. при r>>l0 и r>>l) I sin2q/r2. (23) На рис. 3 приведена зависимость I(q) при фиксированном расстоянии от диполя r. Эту зависимость называют диаграммой направленности излучения диполя. Из нее следует, что диполь всего сильнее излучает в направлениях q =p/2 и 3p/2, а вдоль оси диполя (q = 0, p) диполь не излучает совсем. Рассмотренные выше результаты были использованы в приближенной классической теории излучения атомов, согласно которой это излучение обусловлено колебаниями электронов около их положения равновесия в атомах. В этом случае в формулах (21), (22) p0=еl0 . Итак, движущийся ускоренно электрон в атоме обладает механической энергией W=mv2/2=mw2l02/2, которую он излучает. В связи с этим колебания электрона являются затухающими. Амплитуда колебаний электрона l0 c течением времени уменьшается по закону l0=l00exp(-bt), где b – коэффициент затухания, обусловленного излучением энергии. Промежуток времени t, за который амплитуда колебаний электрона l0уменьшается в е раз (е » 2,72) называют иногда средним временем жизни излучающего атома. Можно показать, что t l2 и, например, для l=5×10-7 м, соответствующей зеленому свету t = 2,25×10-8 с. (24) 18.Применение электромагнитных волн Простейшим излучателем электромагнитных волн является электрический диполь, электрический момент которого изменяется во времени по гармоническому закону где ро — амплитуда вектора р. Примером подобного диполя может служить система, состоящая из покоящегося положительного заряда +Qи отрицательного заряда —Q, гармонически колеблющегося вдоль направления р с частотой со. Задача об излучении диполя имеет в теории излучающих систем важное значение, так как всякую реальную излучающую систему (например, антенну) можно рассчитывать рассматривая излучение диполя. Кроме того, многие вопросы взаимодействия излучения с веществом можно объяснить на основе классической теории, рассматривая атомы как системы зарядов, в которых электроны совершают гармонические колебания около их положений равновесия. Характер электромагнитного поля диполя зависит от выбора рассматриваемой точки. Особый интерес представляет так называемая волновав зова диполя — точки пространства, отстоящие от диполя на расстояниях г, значительно превышающих длину волны (r ≫ l), — так как в ней картина электромагнитного поля диполя сильно упрощается. Это связано с тем, что в волновой зоне диполя практически остаются только «отпочковавшиеся» от диполя, свободно распространяющиеся поля, в то время как поля, колеблющиеся вместе с диполем и имеющие более сложную структуру, сосредоточены в области расстояний r £ l Если волна распространяется в однородной изотропной среде, то время прохождения волны до точек, удаленных от диполя на расстояние r, одинаково. Поэтому во всех точках сферы, центр которой совпадает с диполем, фаза колебаний одинакова, т. е. в волновой зоне волновой фронт будет сферическим и, следовательно, волна, излучаемая диполем, есть сферическая волна. В каждой точке векторы Е и Н колеблются по закону cos(wt—kr), амплитуды этих векторов пропорциональны (1/г)sinq(для вакуума), т. е. зависят от расстояния rдо излучателя и угла qмежду направлением радиуса-вектора и осью диполя. Отсюда следует, что интенсивность излучения диполя в волновой зоне Зависимость (164.1) I от qпри заданном значении r, приводимая в полярных координатах (рис. 228), называется диаграммой направленности излучения диполя. Как видно из выражения (164.1) и приведенной диаграммы, диполь сильнее всего излучает в направлениях, перпендикулярных его оси (q = p/2).Вдоль своей оси (q = 0 и q = p)диполь не излучает вообще. Диаграмма направленности излучения диполя позволяет формировать излучение с определенными характеристиками и используется при конструировании антенн. 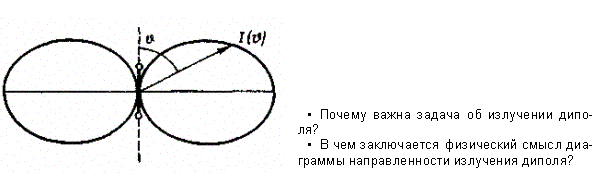 Рис. 228 Впервые электромагнитные волны были использованы через семь лет после опытов Герца. 7 мая 189S т. преподаватель физики офицерских минных классов А. С. Попов (1859—1906) на заседании Русского физико-химического общества продемонстрировал первый в мире радиоприемник, открывший возможность практического использования электромагнитных воли для беспроволочной связи, преобразившей жизнь человечества. Первая переданная в мире радиограмма содержала лишь два слова: «Генрих Герц». Изобретение радио Поповым сыграло огромную роль для распространения и развития теории Максвелла. Электромагнитные волны сантиметрового и миллиметрового диапазонов, встречая на своем пути преграды, отражаются от них. Это явление лежит в основе радиолокации — обнаружения предметов (например, самолетов, кораблей и т. д.) на больших расстояниях и точного определения их положения. Помимо этого, методы радиолокации используются для наблюдения прохождения и образования облаков, движения метеоритов в верхних слоях атмосферы и т. д. Для электромагнитных волн характерно явление дифракции — огибания волнами различных препятствий. Именно благодаря дифракции радиоволн возможна устойчивая радиосвязь между удаленными пунктами, разделенными между собой выпуклостью Земли. Длинные волны (сотни и тысячи метров) применяются в фототелеграфии, короткие волны (несколько метров и меньше) применяются в телевидении для передачи изображений на небольшие расстояния (немногим больше пределов прямой видимости). Электромагнитные волны используются также в радиогеодезии для очень точного определения расстояний с помощью радиосигналов, в радиоастрономии для исследования радиоизлучения небесных тел и т. д. Полное описание применения электромагнитных волн дать практически невозможно, так как нет областей науки в техники, где бы они не использовались. |
