Физике. физика. Электродинамика Электрические токи в металлах, вакууме и газах. Электрический ток в жидкостях
 Скачать 4.58 Mb. Скачать 4.58 Mb.
|
|
Раздел 5 . Тепловое излучение. Оптические системы Методы измерения высоких температур. Пирометры. Совокупность методов измерения высоких температур, использующие зависимость спектральной плотности излучательности или интегральной излучательности тел от температуры называется оптической пирометрией. Приборы для измерения температуры нагретых тел по интенсивности их теплового излучения в оптическом диапазоне спектра называются пирометрами. В зависимости от того, какой закон теплового излучения используется при измерении температуры тел, различают: радиационную, цветовую и яркостную температуры. Радиационная температура. Это такая температура абсолютно черного тела, при которой его излучательность равна излучательности исследуемого тела . В этом случае регистрируется излучательность исследуемого тела и по закону Стефана-Больцмана вычисляется его радиационная температура: 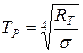 Радиационная температура всегда меньше истинной температуры тела Т. Предположим, что исследуемое тело является серым. Тогда можно записать: С другой стороны: Тогда: Цветовая температура. Для серых тел (или тел, близких к ним по свойствам) спектральная плотность излучательности равна: где 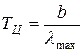 которая называется цветовой температурой. Для серых тел цветовая температура совпадает с истинной температурой. Для тел, которые сильно отличаются от серых (например, обладающие селективным поглощением), понятие цветовой температурой теряет смысл. Измерением цветовой температуры осуществляется оценка температуры Солнца и звезд. Яркостная температура. Яркостная температура – температура абсолютно черного тела, при которой для определенной длины волны его спектральная плотность излучательности равна спектральной плотности излучательности исследуемого тела, то есть: (1.13) где Т – истинная температура тела. По закону Кирхгофа, для исследуемого тела при данной длине волны излучения справедливо: 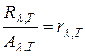 или, учитывая (1.13), получаем: 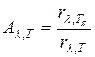 Так как для тел, свойства которых далеки от свойств абсолютно черного тела, , то , следовательно, , то есть истинная температура всегда выше яркостной. Несмотря на некоторую неточность в измерении температуры, пирометрические методы имеют значительные преимущества перед прочими методами измерения. Прежде всего, эти методы являются бесконтактными. И, наконец, позволяют производить измерения температуры тел, удаленных от нас на значительные (космические) расстояния. Фотоэффект Наряду с законами теплового излучения в конце XIX века было открыто и изучено оптическое явление, не укладывающееся в рамки законов классической физики. Это – явление фотоэлектрического эффекта, или, короче, фотоэффекта. Различают фотоэффект внешний, внутренний и вентильный. Внешним фотоэффектом называют испускание электронов веществом (металлом, полупроводником, диэлектриком) под действием электромагнитного излучения. В 1887 г. Герц заметил, что ультрафиолетовое излучение в области ис крового промежутка облегчает разряд. В 1888 г. Гальвакс установил, что причиной этого является появление при облучении свободных зарядов. Первые фундаментальные исследования фотоэффекта выполнены русским ученым А.Г. Столетовым. Принципиальная схема для исследования фотоэффекта приведена на рис.4. Два электрода (катод К из исследуемого материала и анод А – в схеме Столетова применялась металлическая сетка) в вакуумной трубке подключены к батарее так, чтобы с помощью потенциометра R можно изменять не только значение, но и знак подаваемого на них напряжения. Ток, возникающий при освещении катода монохроматическим светом (через кварцевое окошко), измеряется включенным в цепь миллиамперметром. Облучая катод светом различных длин волн, Столетов установил следующие закономерности, не утратившие своего значения до нашего времени: 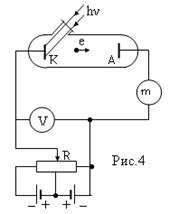 -наиболее эффективное действие оказывает ультрафиолетовое излучение; -наиболее эффективное действие оказывает ультрафиолетовое излучение;-под действием света вещество теряет только отрицательные заряды; -сила тока, возникающего под действием света, прямо пропорциональна его интенсивности. Томсон (1898 г.) измерил удельный заряд частиц, испускаемых под действием света (по отклонению в электрическом и магнитном полях). Эти измерения показали, что под действием света вырываются электроны. 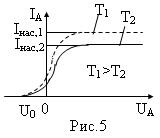 На рис.5 приведена вольт-амперная характеристика фотоэффекта – зависимость фототока IA от напряжения UA между электродами. Приведенные кривые соответствуют двум разным освещенностям катода (двум различным температурам катода), но одинаковой частоте падающего на катод света. С увеличением напряжения фототок постепенно возрастает, т.е. все большее число фотоэлектронов достигает анода. Из пологого характера кривых следует, что электроны вылетают из катода с разными скоростями. Максимальное значение – фототок насыщения – определяется таким значением напряжения, при котором все электроны, испускаемые катодом, достигают анода. На рис.5 приведена вольт-амперная характеристика фотоэффекта – зависимость фототока IA от напряжения UA между электродами. Приведенные кривые соответствуют двум разным освещенностям катода (двум различным температурам катода), но одинаковой частоте падающего на катод света. С увеличением напряжения фототок постепенно возрастает, т.е. все большее число фотоэлектронов достигает анода. Из пологого характера кривых следует, что электроны вылетают из катода с разными скоростями. Максимальное значение – фототок насыщения – определяется таким значением напряжения, при котором все электроны, испускаемые катодом, достигают анода.Из вольтамперной характеристики следует, что при нулевом значении напряжения фототок не исчезает. Это означает, что электроны, выбитые светом из катода, обладают некоторой начальной скоростью, а значит, и отличной от нуля кинетической энергией и могут достигнуть анода без внешнего поля. Чтобы фототок стал равным нулю, необходимо приложить задерживающее напряжение U0. При U=U0 ни один из электронов, даже обладающий при вылете из катода максимальной скоростью Vmax,, не может преодолеть задерживающего поля и достигнуть анода. Следовательно, 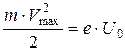 (1.14) (1.14)Измерив задерживающее напряжение, можно определить максимальные значения скорости и кинетической энергии фотоэлектронов. Внешний фотоэффект подчиняется следующим трем законам, полученным из обобщения опытных данных: Из закона Кирхгофа (см. (198.1)) следует, что спектральная плотность энергетической светимости черного тела является универсальной функцией, поэтому нахождение ее явной зависимости от частоты и температуры является важной задачей теории теплового излучения. Австрийский физик Й. Стефан (1835—1893), анализируя экспериментальные данные (1879), и Л. Больцман, применяя термодинамический метод (1884), решили эту задачу лишь частично, установив зависимость энергетической светимости от температуры. Согласно закону Стефана — Больцмана, т. е. энергетическая светимость черного тела пропорциональна четвертой степени его термодинамической температуры; — постоянная Стефана — Больцмана: ее экспериментальное значение равно Закон Стефана — Больцмана, определяя зависимость от температуры, не дает ответа относительно спектрального состава излучения черного тела. Из эксперимен- ныхтемпературах (рис. 287) следует, что распределение энергии в спектре черного тела является неравномерным. Все кривые имеют явно выраженный максимум, который по мере повышения температуры смещается в сторону более коротких волн. Площадь, ограниченная кривой зависимости и осью абсцисс, пропорциональна энер- гетической светимости черного тела и, следовательно, по закону Стефана — Больцмана, четвертой степени температуры. Немецкий физик В. Вин (1864—1928), опираясь на законы термо- и электродинамики, установил зависимость длины волны соответствующей максимуму функции от температуры Т. Согласно закону смещения Вина, т. е. длина волны соответствующая максимальному значению спектральной плотности энергетической светимости черного тела, обратно пропорциональна его термодинамической температуре, — постоянная Вина; ее экспериментальное значение равно  понижении температуры нагретых тел в их спектре все сильнее преобладает длинноволновое излучение (например, переход белого каления в красное при остывании металла,) Формулы Рэлея — Джинса и Планка Из рассмотрения законов Стефана — Больцмана и Вина следует, что термодинамический подход к решению задачи о нахождении универсальной функции Кирхгофа не дал желаемых результатов. Следующая строгая попытка теоретического вывода зависимости принадлежит английским ученым Д. Рэлею и Д. Джинсу (1877—1946), которые применили к тепловому излучению методы статистической физики, воспользовавшись классическим законом равномерного распределения энергии по степеням свободы. Формула Рэлея — Джинса для спектральной плотности энергетической светимости черного тела имеет вид где лятора, совершающего колебания, средние значения кинетической и потенциальной энергий одинаковы (см. § 50), поэтому средняя энергия каждой колебательной степени свободы Как показал опыт, выражение (200.1) согласуется с экспериментальными данными только в области достаточно малых частот и больших температур. В области больших частот формула Рэлея — Джинса резко расходится с экспериментом, а также с законом смещения Вина (рис. 288). Кроме того, оказалось, что попытка получить закон Стефана — Больцмана (см. (199.1)) из формулы Рэлея — Джинса приводит к абсурду. Действительно, вычисленная с использованием (200.1) энергетическая светимость черного тела (см. (198.3)) в то время как по закону Стефана — Больцмана пропорциональна четвертой степени температуры. Этот результат получил название «ультрафиолетовой катастрофы». Таким образом, в рамках классической физики не удалось объяснить законы распределения энергии в спектре черного тела. В области больших частот хорошее согласие с опытом даетформула Вина (закон излучения Вина),полученная им из общих теоретических соображений: где — спектральная плотность энергетической светимости черного тела, С и А— постоянные величины. В современных обозначениях с использованием по- 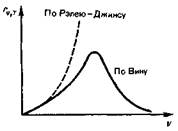 стоянной Планка, которая в то время еще не была известна, закон излучения Вина может быть записан ввиде Правильное, согласующееся с опытными данными выражение для спектральной плотности энергетической светимости черного тела было найдено в 1900 г. немецким физиком М. Плавком. Для этого ему пришлось отказаться от установившегося положения классической физики, согласно которому энергия любой системы может изменяться непрерывно, т. е. может принимать любые сколь угодно близкие значения. Согласно выдвинутой Планком квантовой гипотезе, атомные осцилляторы излучают энергию не непрерывно, а определенными порциями — квантами, причем энергия кванта пропорциональна частоте колебания (см. (170.3)): где ями, то энергия осциллятора может принимать лишь определенные дискретные значения, кратные целому числу элементарных порций энергии В данном случае среднюю энергию осциллятора нельзя принимать равной В приближении, что распределение осцилляторов по возможным дискретным состояниям подчиняется распределению Больцмана (§ 45), средняя энергия осциллятора а спектральная плотность энергетической светимости черного тела Таким образом, Планк вывел для универсальной функции Кирхгофа формулу которая блестяще согласуется с экспериментальными данными по распределению энергии в спектрах излучения черного тела во всем интервале частот и температур. Теоретический вывод этой формулы М. Планк изложил 14 декабря 1900 г. на заседании Немецкого физического общества. Этот день стал датой рождения квантовой физики. В области малых частот, т. е. при теплового движения kТ), формула Планка (200.3) совпадает с формулой Рэлея — Джинса (200.1). Для доказательства этого разложим экспоненциальную функцию в ряд, ограничившись для рассматриваемого случая двумя первыми членами: Подставляя последнее выражение в формулу Планка (200.3), найдем, что т. е. получили формулу Рэлея — Джинса (200.1). Из формулы Планка можно получить закон Стефана — Больцмана. Согласно (198.3) и (200.3), 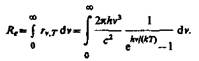 Введем безразмерную переменную Формула для преоб- разуется к виду  где 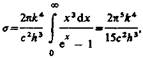 так как так как 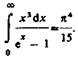 Таким образом, действительно формула Таким образом, действительно формулаПланка позволяет получить закон Стефана — Больцмана (ср. формулы (199.1) и (200.4)). Кроме того, подстановка числовых значений значение, хорошо согласующееся с экспериментальными данными. Закон смещения Вина получим с помощью формул (197.1) и (200.3): откуда 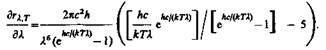 Значение при котором функция достигает максимума, найдем, приравняв нулю эту произ- водную. Тогда, введя Решение этого трансцендентного уравнения методом последовательных приближений дает х=4,965. Следовательно, т. е. получили закон смещения Вина (см. (199.2)). Из формулы Плавка, зная универсальные постоянные постоянные Стефана — Больцмана и Вина С другой стороны, зная экспериментальные значения Таким образом, формула Планка не только хорошо согласуется с экспериментальными данными, но и содержит в себе частные законы теплового излучения, а также позволяет вычислить постоянные в законах теплового излучения. Следовательно, формула Планка является полным решением основной задачи теплового излучения, поставленной Кирхгофом. Ее решение стало возможным лишь благодаря революционной квантовой гипотезе Планка. 2.Тепловые источники света. |
