Лачин Электроника. Электроника рекомендовано Министерством образования Российской Федерации в качестве учебного пособия ля студентов высших технических учебных заведений РостовнаДону Феникс 2001 Рецензенты

• Название: Электроника рекомендовано Министерством образования Российской Федерации в качестве учебного пособия ля студентов высших технических учебных заведений РостовнаДону Феникс 2001 Рецензенты
• Анкор: Лачин Электроника.doc
• Дата: 28.01.2017
• Размер: 7.57 Mb.
• Имя файла: Лачин Электроника.doc
• Тип: Учебное пособие; #535
• страница: 11 из 17

2.8. АКТИВНЫЕ ФИЛЬТРЫ

Фильтром называют устройство, которое передает (пропускает) синусоидальные сигналы в одном определен­ном диапазоне частот (в полосе пропускания) и не пере­дает (задерживает) их в остальном диапазоне частот (в полосе задерживания). Естественно, фильтры используют для передачи не только синусоидальных сигналов, но, определяя полосы пропускания и задерживания, ориенти­руются именно на синусоидальные сигналы. Зная, как фильтр передает синусоидальные сигналы, обычно доста­точно легко определить, как он будет передавать сигналы и другой формы. В устройствах электроники фильтры используются очень широко. Различают аналоговые и циф­ровые фильтры. В аналоговых фильтрах обрабатываемые сигналы не преобразуют в цифровую форму, а в цифровых перед обработкой сигналов осуществляют такое преобра­зование.

Ниже рассматриваются аналоговые фильтры. Такие фильтры строят на основе как пассивных (конденсаторов, катушек индуктивности, резисторов), так и активных эле­ментов (транзисторов, операционных усилителей). Для аналоговой фильтрации широко используют также элек­тромеханические фильтры: пьезоэлектрические и механи­ческие. В пьезоэлектрических фильтрах используют есте­ственный и искусственный кварц, а также пьезокерамику. Основу механического фильтра составляет то или'иное механическое устройство.

Важно различать требования, предъявляемые к фильт­рам силовой и информативной (информационной) элек­троники. Фильтры силовой электроники должны иметь как можно больший коэффициент полезного действия. Для них очень важной является проблема уменьшения габаритных размеров. Такие фильтры часто строят на ос­нове только пассивных элементов. К фильтрам силовой электроники относятся сглаживающие фильтры, рассмат­риваемые при изучении вторичных источников питания. Фильтры информативной электроники чаще разрабатыва­ют при использовании активных элементов. При этом широко используют операционные усилители.

Фильтры, содержащие активные элементы, называют активными. Ниже рассматриваются активные фильтры, в которых обычно не используются катушки индуктивнос­ти. Поэтому они могут быть изготовлены с применением технологии интегральных микросхем (катушки с большой индуктивностью не удается изготовить по указанной тех­нологии). Нередко активные фильтры оказываются де­шевле соответствующих фильтров на пассивных элемен­тах и занимают меньшие объемы. Активные фильтры способны усиливать сигнал, лежащий в полосе пропуска­ния. Во многих случаях их достаточно легко настроить. Укажем также и недостатки активных фильтров:

• 
  использование источника питания;
  
• 
  невозможность работы на таких высоких частотах, на которых используемые операционные усилители уже не способны усиливать сигнал.
  

2.8.1. Общее математическое описание фильтров

Фильтры вообще и активные фильтры, в частности, яв­ляются настолько важными устройствами электроники, что вопросам их строгого, математического описания уде­лялось и уделяется самое серьезное внимание. Публику­ется большое число научных статей и книг, посвященных фильтрам. Для того, чтобы инженер или научный работ­ник был в состоянии воспользоваться указанными источ­никами информации, а также средствами автоматизиро­ванного проектирования, он должен хотя бы в общих чертах знать особенности математического описания фильтров.

Обычно фильтр анализируется как конечная линейная электронная схема с сосредоточенными параметрами. Если реальная схема фильтра является нелинейной (на­пример, содержит транзисторы или операционные усили­тели), то при анализе она линеаризуется и затем рассмат­ривается как линейная.

В соответствии с изложенным фильтр описывается обыкновенным линейным дифференциальным уравнени­ем некоторого порядка n

где х = x(t) — входной сигнал фильтра (обычно — вход­ное напряжение);

y = y(t) — выходной сигнал фильтра (обычно — выход­ное напряжение);

а_i,i=0,...,n; b_i ,i = 0,...,m— вещественные коэффициен­ты.

Для фильтров, которые могут быть реализованы, вы­полняется соотношение п>т. Величину я называют так­же порядком фильтра. Если, например, n = 2, то говорят, что фильтр второго порядка.

Необходимо отметить, что вместо записанного одного уравнения фильтр может быть описан линейной системой из п дифференциальных уравнений первого порядка (си­стемой дифференциальных уравнений в форме Коши). Показано, что величина и равна или меньше количества реактивных элементов (конденсаторов и катушек индук­тивности) фильтра. Например, если в фильтре три конден­сатора, то он может быть третьего или меньшего поряд­ка. Инженеру нужно знать, что порядок фильтра определяется количеством тех напряжений на конденса­торах и токов катушек индуктивности, которые могут за­даваться как начальные независимо друг от друга.

Для примера обратимся к схеме, приведенной на рис. 2.48.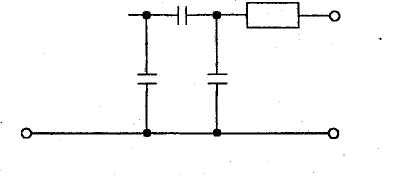



Уже до составления одного дифференциального урав­нения или эквивалентной системы дифференциальных уравнений можно сказать, что это схема второго порядка, так как начальные напряжения при расчете переходного процесса можно задавать независимо для двух из трех кон­денсаторов.

Применим к приведенному выше уравнению прямое преобразование Лапласа и определим передаточную фун­кцию T(s) как отношение операторного изображения Y(s) выходной величины к операторному изображению X(s) входной величины: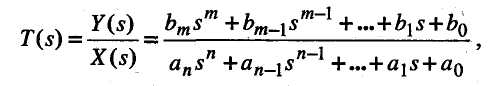


где s— комплексная частота.

Запишем передаточную функцию в следующем виде:



где К— вещественный коэффициент; z₁...z_m — ...корни полинома числителя (их принято называть нулями);

p₁...p_n — корни полинома знаменателя (их принято назы­вать полюсами).

Известно, что полюсы и нули могут быть или веще­ственными, или комплексно-сопряженными.

Как уже отмечалось, при описании свойств фильтров обычно ориентируются на синусоидальные сигналы. При этом имеют в виду установившийся режим работы. В та­кой ситуации широко используют частотную передаточ­ную функцию T(jw), которую получают из обычной пе­редаточной функции при использовании подстановки

s =jw,

где w— круговая частота, рад/сек.

Получаем



Укажем три характеристики, которые широко исполь­зуются для описания фильтров:

• 
  амплитудно-частотная;
  
• 
  фазочастотная;
  
• 
  времени замедления (группового времени замедления).
  

Амплитудно-частотная характеристика представляет собой зависимость вида



Значение А(w) на некоторой частоте дает отношение действующих (и амплитудных) значений сигналов на вы­ходе и входе фильтра. На практике широко используют амплитудно-частотную характеристику в децибелах, кото­рая представляет собой зависимость вида



Фазочастотная характеристика — это зависимость вида



Значение φ{w) на некоторой частоте является сдвигом по фазе выходной величины по отношению ко входной.

Характеристика времени замедления — это зависи­мость вида


Величина т(w)— это время замедления (групповое). Оно характеризует сдвиг по времени выходной величины по отношению к входной.

Наиболее широко используют амплитудно-частотную и фазочастотную характеристики. Характеристика време­ни замедления не несет принципиально новой информа­ции по сравнению с фазочастотной характеристикой, но является весьма полезной и используется достаточно час­то. Для уяснения роли времени замедления при анализе фильтров кратко рассмотрим проблему искажения формы сигнала, содержащего несколько гармоник, при прохож­дении его через фильтр. Напомним, что фильтр рассмат­ривается как линейное устройство, поэтому речь идет не о нелинейных искажениях. Имеются в виду искажения, причиной которьк является несовершенство фазочастот-ной характеристики фильтра.

Вначале рассмотрим фильтр с настолько совершенной фазочастотной характеристикой, что искажение формы сигнала отсутствует. Такая фазочастотная характеристика является линейной однородной функцией круговой частоты и определяется выражением

φ(w) = —кw,

где к — постоянная положительная величина. Приведем соответствующий график (рис. 2.49). Пусть входным сиг­налом является напряжение и_вх, содержащее две гармони­ки (рис. 2.50):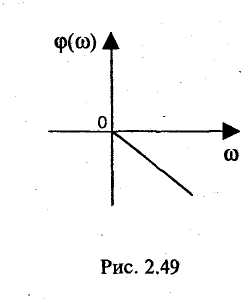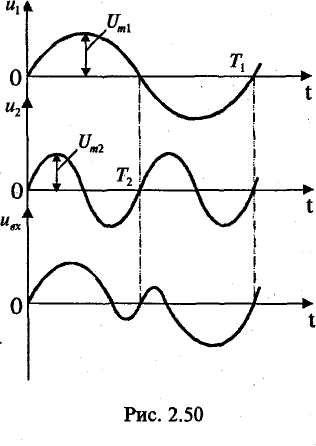

Для первой гармоники фильтр обеспечивает сдвиг по фазе φ₁(w) = —кw₁, а для второй гармоники сдвиг по фазе будет равен φ₂(w) = —кw₂ = —2кw₁. Обозначим через Т₁, и Т₂периоды соответственно первой и второй гармоник, а через f₁ и f₂ — их частоты. Определим сдвиги по времени t₁и t₂, соответствующие сдвигам по фазе φ₁ и φ₂. Обратим­ся к первой гармонике. Для нее сдвиг по фазе —2π соот­ветствует периоду Т₁асдвиг по фазе φ₁, соответствует ис­комому времени t₁.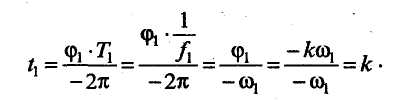

Составим пропорцию

отсюда
Аналогично получаем


Таким образом, в рассматриваемом случае гармоники будут сдвинуты по времени на одну и ту же величину к и поэтому сигнал не будет искажен, т. е. форма его останет­ся прежней. Но, естественно, выходной сигнал будет сдви­нут относительно входного на время +к (в рассматривае­мом случае выходной сигнал будет отставать от входного на время к).

Определим для рассматриваемого фильтра время замед­ления:
Таким образом, в рассматриваемом случае время замед­ления — это время, на которое выходной сигнал будет сдвинут относительно входного.

Если фазочастотная характеристика не будет линейной однородной функцией круговой частоты, то различные гармоники будут сдвинуты фильтром на различные отрез­ки времени, и поэтому форма сигнала, содержащего не одну гармонику, будет искажаться. Чем ближе фазочастот­ная характеристика некоторого фильтра к линейной одно­родной функции (и чем меньше значения времени замед­ления отличаются от некоторой константы), тем искажения будут меньше.

Поэтому при использовании систем автоматизирован­ного проектирования (САПР) характеристику времени за­медления часто выводят на экран компьютера и исполь­зуют для оценки искажений сигналов фильтром. Время замедления называют также временем запаздывания.

Из изложенного следует, что частотные характеристи­ки фильтра полностью определяются значением коэффи­циента К передаточной функции, а также значением ее нулей и полюсов. Нули и полюсы часто изображают в виде точек на плоскости комплексной частоты (s-плоскости), получая так называемую диаграмму нулей и полюсов. Та­кая диаграмма вместе с коэффициентом К несет полную информацию о частотных свойствах фильтра. Имея диаг­рамму нулей и полюсов, легко определить значения мо­дуля и аргумента частотной передаточной функции, т. е. коэффициент усиления и сдвиг по фазе.

Д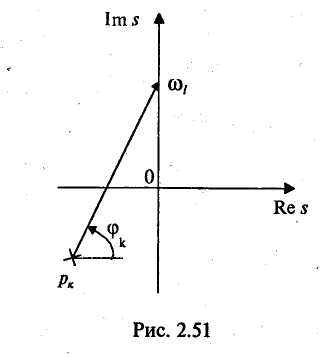опустим, что некоторый полюс р_красположен на s-плоскости так, как показано на рис. 2.51. Пусть круго­вая частота равна w₁. Тогда для учета полюса р_кв знамена­тель дроби, определяющей величину |T(jw)|, следует до­бавить сомножитель, равный длине вектора с началом в полюсе р_ки окончанием на мнимой оси с ординатой w₁, а в алгебраическую сумму, определяющую величину

argT(jw), следует добавить слагаемое —φ_к ,где φ_к— угол, указанный на рисунке.

2.8.2. Классификация фильтров по виду их амплитудно-частотных характеристик

Рассмотрим основные типы фильтров, классифициру­емых по виду амплитудно-частотных характеристик.

Фильтры нижних частот. Для фильтров нижних час­тот (ФНЧ) характерно то, что входные сигналы низких ча­стот, начиная с постоянных сигналов, передаются на вы­ход, а сигналы высоких частот задерживаются.

Приведем примеры амплитудно-частотных характери­стик фильтров нижних частот. На рис. 2.52, а показана ха­рактеристика идеального (не реализуемого на практике) фильтра (ее иногда называют характеристикой типа «кир­пичная стена»). На других рисунках представлены харак­теристики реальных фильтров.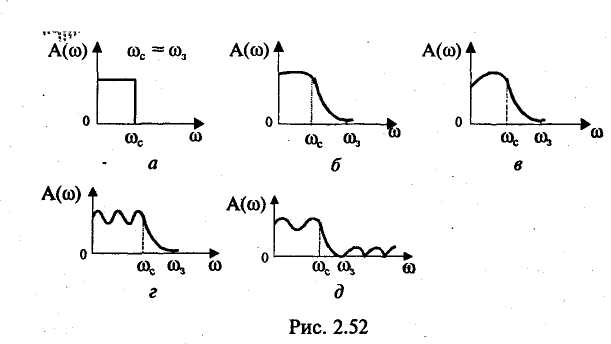

Полоса пропускания лежит в пределах от нулевой час­тоты до частоты среза w_с. Обычно частоту среза определя­ют как частоту, на которой величина А(w) равна 0,707 от максимального значения (т. е. меньше максимального зна­чения на 3 дБ).

Полоса задерживания (подавления) начинается от ча­стоты задерживания w₃ и продолжается до бесконечности. В ряде случаев частоту задерживания определяют как ча­стоту, на которой величина А(w) меньше максимального значения на 40 дБ (т. е. меньше в 100 раз).

Между полосами пропускания и задерживания у реаль­ных фильтров расположена переходная полоса. У идеаль­ного фильтра переходная полоса отсутствует.

Фильтры верхних частот. Фильтр верхних частот ха­рактерен тем, что он пропускает сигналы верхних и задер­живает сигналы нижних частот.

Частотные характеристики фильтров верхних частот, как и характеристики фильтров нижних частот, много­образны в своих деталях.

И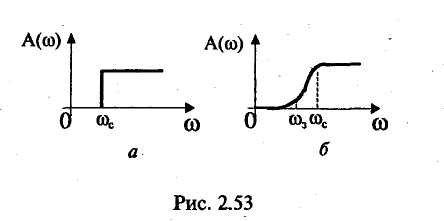зобразим для иллюстрации две характеристики: иде­альную, нереализуемую (рис. 2.53, а), и одну из типичных реальных (рис. 2.53, б). Через w_с и w₃ обозначены частоты среза и задерживания.

Полосовые фильтры (полосно-пропускающие). Полосовой фильтр пропускает сигналы одной полосы частот, распо­ложенной в некоторой внутренней части оси частот. Сиг­налы с частотами вне этой полосы фильтр задерживает.

Изобразим амплитудно-частотную характеристику для идеального (нереализуемого) фильтра (рис. 2.54, а) и одну из типичных реальных характеристик (рис. 2.54, б). Через w_с1и w_с2обозначены две частоты среза, w₀— средняя час­тота. Она определяется выражением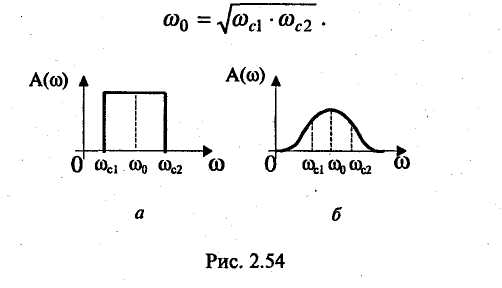



Р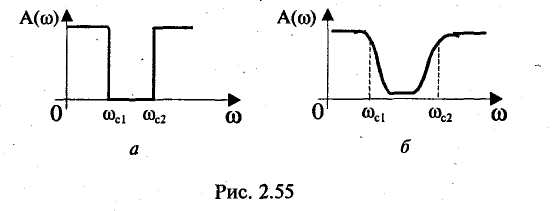ежекторные фильтры (полосно-заграждающие). Режекторные фильтры не пропускают (задерживают) сигна­лы, лежащие в некоторой полосе частот, и пропускают сигналы с другими частотами. Изобразим амплитудно-частотную характеристику для идеального (нереализуемо­го) фильтра (рис. 2.55, а) и одну из типичных реальных характеристик (рис. 2.55, б).

Всепропускающие фильтры (фазовые корректоры). Эти фильтры пропускают сигналы любой частоты. Построим соответствующую амплитудно-частотную характеристику (рис. 2.56). Такие фильтры используются в некоторой электронной системе для того, чтобы изменить с той или иной целью фазочастотную характеристику всей системы.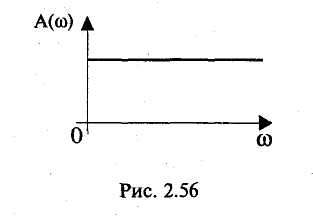


Исходя из приведенного выше математического описа­ния фильтров, нетрудно сделать вывод, что ход амплитуд­но-частотной характеристики на достаточном удалении от полосы пропускания прямо определяется порядком филь­тра. Этот факт хорошо иллюстрируют амплитудно-частот­ные характеристики, выполненные в логарифмическом масштабе. Рассмотрим указанные характеристики для не­которых фильтров различного порядка, имеющих одина­ковые коэффициенты усиления на нулевой частоте, рав­ные 100 (рис. 2.57).

Из математического описания следует, что на достаточ­ном расстоянии от полосы пропускания наклон характеристики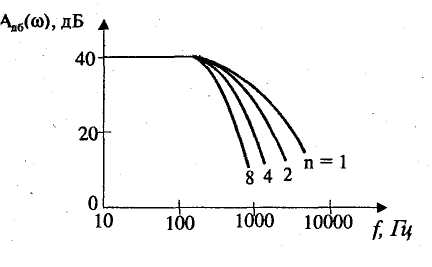




равен —20n дБ/дек, где п — порядок фильтра. Наклон —20 дБ/дек означает, что увеличение частоты в 10 раз приводит к уменьшению коэффициента усиления в 10 раз, а наклон —40 дБ/дек означает, что увеличение часто­ты в 10 раз приводит к уменьшению коэффициента уси­ления в 100 раз.

Из изложенного следует, что если необходимо обеспе­чить более быстрое изменение коэффициента усиления на удалении от полосы пропускания, то следует увеличить по­рядок фильтра (но при этом схема фильтра усложняется).

2.8.3. Классификация фильтров

по особенностям полиномов, входящих в передаточные функции

Рассмотрим эту классификацию на примере фильтров низкой частоты. Свойства фильтров сильно зависят от того, какими полиномами описываются их передаточные функции, или, другими словами, от того, как расположе­ны нули и полюсы на плоскости комплексной частоты. Указанные особенности математического описания опре­деляют ход амплитудно-частотных характеристик в поло­се пропускания и в переходной полосе. Ход характерис­тик на удалении от полосы пропускания, как уже отмечалось, определяется порядком фильтра.

На практике широко используются фильтры, отлича­ющиеся характерными особенностями полиномов переда­точных функций. Это фильтры Баттерворта, Чебышёва, Бесселя (Томсона).

Для фильтров Баттерворта характерно то, что полюсы лежат на полуокружности в левой половине s-плоскости. Полюсы фильтра Чебышёва расположены на части эллип­са. Полюсы фильтра Бесселя расположены на кривой, ле­жащей вне указанной полуокружности. Сказанное иллю­стрируется на рис. 2.58. Характер расположения полюсов определяет следующие особенности этих фильтров.

Фильтры Баттерворта характеризуются наиболее плос­кой амплитудно-частотной характеристикой в полосе пропускания. Это их достоинство. Но в переходной полосе
указанные характеристики спадают плавно, недостаточно резко.

Фильтры Чебышёва отличаются резким спадом ампли­тудно-частотных характеристик в переходной полосе, но в полосе пропускания эти характеристики не являются плоскими.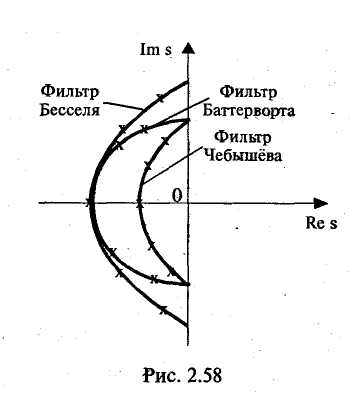



Фильтры Бесселя характеризуются очень пологими уча­стками амплитудно-частотных характеристик в переход­ной полосе, еще более пологими, чем у фильтров Баттер-ворта. Их фазочастотные характеристики достаточно близки к идеальным, соответствующим постоянному времени за­медления, поэтому такие фильтры мало искажают форму входного сигнала, содержащего несколько гармоник.

Изобразим амплитудно-частотные характеристики фильтров указанных типов (рис. 2.59). Предположим, что все фильтры имеют одинаковый порядок и близкие коэф­фициенты усиления в полосе пропускания. Для того, что­бы характеристики были особенно наглядными, восполь­зуемся линейным масштабом.

Полезно выполнить сравнение типов фильтров и по их переходным характеристикам (т. е. во временной области).

Н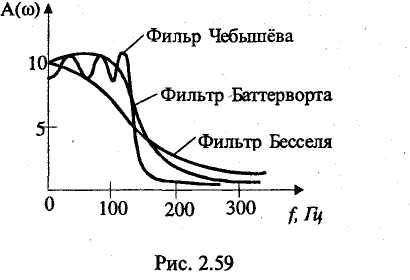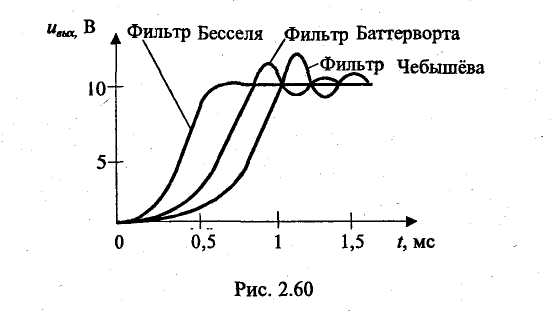а рис. 2.60 показаны типичные переходные характе­ристики фильтров, т. е. временные диаграммы выходных напряжений при ступенчатом изменении входных напря­жений. Из рисунка следует, что во временной области фильтр Бесселя имеет наилучшие свойства, фильтр Чебышёва — наихудшие свойства, а фильтр Баттерворта по сво­им свойствам занимает промежуточное положение.

2.8.4. Особенности проектирования активных фильтров

Технические требования при проектировании актив­ных фильтров обычно определяют основные параметры амплитудно-частотной и фазочастотной характеристик, а также другие требования, наиболее важные для заказчи­ка. Среди указанных других требований часто фигуриру­ют требования в отношении чувствительности частотных характеристик к изменению параметров элементов, входящих в фильтр (сопротивлений резисторов, емкостей конденсаторов и т. д.). Если чувствительность высока, то фильтр может потребовать сложной настройки, и суще­ствует опасность, что в процессе его эксплуатации при ста­рении элементов свойства фильтра начнут изменяться.

При проектировании фильтров высокого порядка п часто используют следующий подход. Вначале будем счи­тать, что n — четное число. Передаточную функцию T(s) представляют в виде произведения сомножителей, причем каждый сомножитель является передаточной функцией второго порядка: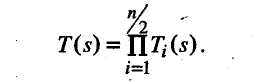



При этом фильтр порядка п строится как схема, состо­ящая из каскадов в количестве n/2, причем каждый кас­кад является фильтром второго порядка и соответствует определенному сомножителю T_i (s). Часто используют одну и ту же базовую схему для всех каскадов. Параметры элементов этой схемы (сопротивления резисторов и емко­сти конденсаторов) для каждого i-го каскада определяют так, чтобы каскад описывался передаточной функцией T_i(s). В общем случае параметры элементов различных каскадов различны. Если число и нечетное, то в схему фильтра до­полнительно включают один каскад, являющийся цепью первого порядка.

2.8.5. Схемы активных фильтров

Приведем в качестве примера две схемы фильтров вто­рого порядка.

Вначале изобразим схему фильтра нижних частот (рис. 2.61). Можно заметить, что на низких частотах (и на по­стоянном токе) фильтр имеет коэффициент усиления, который оисывается следующим выражением:
где К — величина, определяющая сопротивление в цепи обратной связи (К— 1)R (рис. 2.61).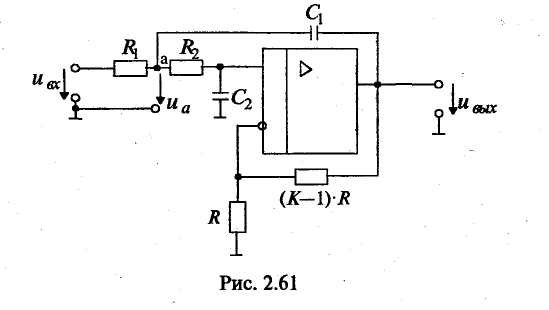



Приведенное выражение соответствует неинвертирую-щему усилителю.

При увеличении частоты входного сигнала напряжение на выходе уменьшается. Укажем две причины этого умень­шения. Во-первых, уменьшается напряжение на неинвер-тирующем входе (т. е. на емкости С₂) из-за уменьшения модуля комплексного сопротивления емкости С₂. Во-вто­рых, уменьшается напряжение и_аиз-за того, что модуль комплексного сопротивления емкости С₁уменьшается и через эту емкость с выхода усилителя в точку «а» подает­ся ток, который значительно сдвинут по фазе относитель­но напряжения и_вх.

Далее рассмотрим схему фильтра верхних частот (рис. 2.62). На высоких частотах коэффициент усиления филь­тра равен К. Рассмотренные фильтры могут составлять основу фильтров Баттерворта, Чебышёва, Бесселя или фильтров другого типа в зависимости от параметров рези­сторов R₁ и R₂ конденсаторов С₁и С₂.

Краткая характеристика активных фильтров на пере­ключаемых конденсаторах. Переключаемый конденсатор — это своего рода дозатор, передающий строго определен­ные заряды из одной электрической цепи в другую. Изоб­разим упрощенную схему, поясняющую работу переклю­чаемого конденсатора (рис. 2.63). Ключи S₁и S₂работают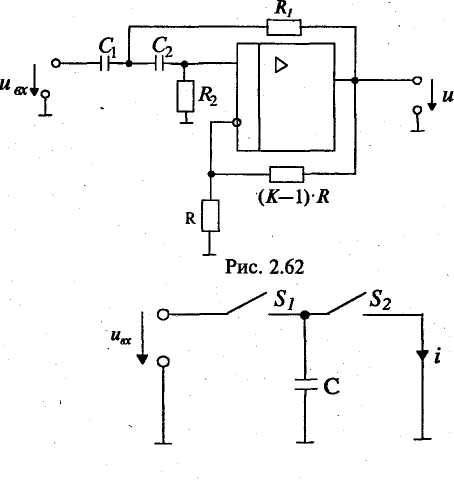



в противофазе, т. е. когда ключ S₁замкнут, ключ S₂разом­кнут, и наоборот. После замыкания ключа S₁конденсатор накапливает заряд и_вхС, получая его от источника входно­го напряжения. После замыкания ключа S₂конденсатор отдает указанный заряд в цепь этого ключа. Чем чаще бу­дут переключаться ключи, тем больший заряд в единицу времени будет передаваться в указанную цепь, т. е. тем больше будет среднее значение тока i. Использование пе­реключаемого конденсатора позволяет изменять среднее значение тока i путем изменения частоты переключения. В этом смысле переключаемый конденсатор играет роль резистора с регулируемым сопротивлением.

Активные фильтры на переключаемых конденсаторах имеют следующие достоинства:

• они достаточно дешевые, так как при их изготовлении используется относительно простая технология;

• их легко перестраивать на другие частоты, для чего достаточно изменять частоту переключения. Активные фильтры на переключаемых конденсаторах уже довольно долго используются на практике.